SIMULACION BORROSA DE UN REACTOR CON REACCION EXOTERMICA NO LINEAL

FUZZY SIMULATION OF AN EXOTHERMIC NONLINEAR REACTOR

 

MIGUEL ANGEL RODRIGUEZ BORROTO
Facultad de Ingeniería Eléctrica, Ph.D, Universidad Central de las Villas, Santa Clara, Cuba, marodrig@uclv.edu.cu

JOSE RAFAEL ABREU GARCIA
Facultad de Ingeniería Eléctrica, Ph.D, Universidad Central de las Villas, Santa Clara, Cuba

ROBERTO BACA GOMEZ
Departamento de Ingeniería Electrónica, Msc, Instituto Tecnológico de Toluca, Estado de México

BORIS LUIS MARTINEZ JIMENEZ
Facultad de Ingeniería Eléctrica, Msc, Universidad Central de las Villas, Santa Clara, Cuba

 

Recibido para revisar febrero 09 de 2007, aceptado abril 04 de 2007, versión final julio 06 de 2007

 

---

RESUMEN: En el presente trabajo se desarrolla un modelo difuso basado en la estructura Takagi-Sugeno-Kang dinámica para un reactor continuo de tanque con agitador (RCTA) con reacción química de primer orden exotérmico. A partir de datos experimentales obtenidos mediante simulación del proceso real, se obtiene la base de datos de las variables de entrada y salida del proceso y a partir de la misma se elaboran los archivos de datos de entrenamiento y de verificación del modelo borroso el cual es obtenido mediante la herramienta anfis de MATLAB. El modelo obtenido permite predecir la salida del sistema con errores de predicción muy bajos, por lo que el mismo sienta las bases para el diseño de un controlador predictivo no lineal del mismo en próximas etapas de la investigación.

PALABRAS CLAVE: Identificación de Sistemas, Lógica Borrosa, Modelado, Modelado Borroso, Simulación.

ABSTRACT: In this paper a fuzzy model based on dynamic Takagi-Sugeno-Kang framework of a continuous stirred tank reactor (CSTR) with exothermic fist order chemical reaction is carried out. From experimental data base obtained through real process simulation for input and output variables, the training and checking files of the fuzzy model were developed. Theses files allow us to carried out the fuzzy model by mean of the anfis tool of MATLAB. The model obtained allow us to predict the system out put with a very small prediction error for that reason this model is very important to design a nonlinear predictive control based fuzzy model to this process in future research stages.

KEYWORDS: Systems Identification, Fuzzy Logic, Fuzzy Modelling, Simulation.

---

 

1. INTRODUCCION

Para generar automáticamente modelos borrosos a partir de mediciones físicas se han desarrollado varios métodos. A saber; por agrupamiento ([1],…,[13]), métodos de ortogonalización ([14],…,[18]), métodos estadísticos [19], y los llamados sistemas híbridos ([20],…,[25]) que combinan varias técnicas de inteligencia artificial. En el presente trabajo se aplica el modelo dinámico de Takagi-Sugeno-Kang (TSK) [26], [27] para la obtención un modelo borroso del proceso que tiene lugar en cierto reactor químico continuo de tanque con agitador (RCTA), con reacción exotérmica de primer orden, para ser utilizado como predictor no lineal del proceso

En cuestión, con el objetivo de ser utilizado posteriormente, en el diseño de un Controlador Predictivo basado en el Modelo (CPM). Esta estrategia computacional para el control de procesos industriales se desarrolla y refirma vertiginosamente, tanto académica como paracticamente, y su complementación con los procedimientos para el desarrollo de modelos dinámicos basados en lógica borrosa [28], [29] la reafirma e incentiva para continuar su estudio y desarrollo.

En este artículo se encausa el modelo del proceso en su justa dimensión no lineal, basado en sistema de inferencia borroso con lo cual se logra mayor robustez, tanto en la estabilidad como en el desempeño cuando se le compara, mediante simulación, con un CPM basado en modelos lineales de predicción. El problema ha sido abordado en otras oportunidades [30], [31]. En el primero, considerando al proceso como un sistema simple entrada simple salida (SESS) tomando como variable de entrada el caudal de refrigerante en el sistema de enfriamiento del reactor y como salida la concentración de reactivo en el mismo. En el segundo, caso considerando el sistema multivariable no lineal pero con un predictor no-borroso. Sin embargo, en el presente trabajo consideramos al proceso excitado, además, por el flujo de alimentación de reactivo; de modo que se considera al sistema como uno de múltiples entradas y una salida, la concentración de reactivo (sistema MISO), lo cual se considera muy acorde con la operación del proceso.

 

2. MODELO DEL PROCESO

Se simula el reactor continuo de tanque con agitador no lineal que se muestra esquemáticamente en la Fig. 1, con el objeto de crear una base de datos de entrada-salida apropiada para la elaboración de un modelo borroso.

Figura 1. Reactor continuo de tanque agitado.
Figure 1. Continuous stirred tank reactor.

A partir de las ecuaciones de balance de masa total y del reactivo, de energía en el reactor y la de balance de energía en la chaqueta, así como la expresión de la cinética a través de la ecuación de Arrhuenius se obtiene:

Donde:

h: Nivel de líquido en el reactor (m).
F_i: Flujo volumétrico de entrada (m³/min).
F: Flujo volumétrico de salida (m³/min).
F_c: Flujo volumétrico de refrigerante (m³/min)
C_a: Concentración de reactivo en la mezcla.
C_ai: Concentración de reactivo en la corriente de entrada.
T: Temperatura absoluta de la mezcla reaccionante (ºK).
T_c: Temperatura absoluta del refrigerante (ºK).
T_ci: Temperatura absoluta del refrigerante en la entrada (ºK).
T_i: Temperatura absoluta de la corriente de entrada (ºK).
A_b: Area de la sección uniforme del tanque (m²)
A: Superficie calórica de la chaqueta de enfriamiento (m²).
U: Coeficiente global de transferecncia de calor (kcal/min-ºK- m²).
r: Densidad de la mezcla (kg/m³).
r_c: Densidad del líquido refrigerante (kg/m³).
C_p: Capacidad calórica (kcal/kg-ºK).
C_pc: Capacidad calórica del refrigerante (kcal/kg-ºK).
J: Coeficiente que depende del calor de la reacción (kcal/kg-mol).
k_o: Coeficiente cinético de la reacción (min^-1).
E: Energía de activación (kcal/kg-mol).
R: Constante universal de los gases (kcal/kg-mol-ºK).
V_ch: Volumen de la chaqueta de enfriamiento (m³).

Obsérvese la naturaleza intrínsicamente no lineal del proceso.

2.1 Simulación del Sistema
El modelo no lineal anterior se simula en SIMULINK.

Considerando como variable de salida la concentración del reactivo x₂₂ y tomando como variables de control las u₂₂ y u₃₃ (flujo de alimento de reactivo y flujo de refrigerante). El flujo de salida u₁₁ se deja libre y se considera constante en el valor de estado estable (10 m³/min). El diagrama de simulación se indica en la Fig.2.

Figura 2. Simulación del RCTA.
Figure 2. CSTR simulation.

Para las variables de entrada u₂₂ y u₃₃ se generan señales de ruido seudo aleatorios con frecuencia 3 rad/min y varianza 1 (para ambas señales) y valores promedio de 10.7 m³/min en u₂₂ y 15 m³/min en u₃₃. La simulación se realiza durante 360 min. Se registran las entradas y las salidas y se almacenan en el espacio de trabajo de MATLAB con un periodo de muestro de 0.5 min, tomándose 720 muestras.

2.2 Obtención del Modelo Borroso Takagi_Sugeno_Kang (TSK)

2.2.1 Sistemas de Inferencia Borrosa
Se entiende por Sistema de Inferencia Borrosa al ambiente computacional cuya estructura básica esta formada por tres componentes [32].

A saber:

• Una base de reglas, que son el corazón del FIS y que contiene una serie de reglas del tipo “IF – THEN”.
• Una base de datos, el cual define las funciones de pertenencia utilizadas en las reglas.
• Un mecanismo de inferencia, el cual a través de las reglas, obtiene una salida razonable.

Los modelos borrosos o difusos (fuzzy) usan reglas “IF-THEN” para establecer relaciones cualitativas entre las variables. Un modelo borroso consiste de múltiples reglas y cada una de ellas posee un antecedente y un consecuente. El antecedente especifica una cierta parte del espacio de entrada, mientras que el consecuente es un modelo de regresión donde, algunos valores de entrada son utilizados. La naturaleza basada en reglas de los modelos borrosos permite el uso de información basada en forma de sentencias de lenguaje natural y en consecuencia, hacen los modelos mas transparentes al análisis y a la interpretación.

2.2.2 Modelo borroso Takagi_Sugeno_Kang
El sistema borroso TSK puede ser considerado como una combinación de modelación lingüística y modelación matemática de regresión en el sentido de que el antecedente describe regiones difusas del espacio de entrada donde el consecuente funcional es valido. Las reglas en este tipo de sistema son de la forma:

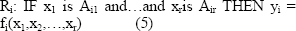
Donde los A_ij son conjuntos borrosos y f_i son funciones reales; para todo i, j enteros reales. Generalmente los f_i son polinomios en las variables de entrada x₁,…,x_r.

La funciones f_i de un modelo son generalmente de la misma estructura, cambiando solamente los parámetros de cada regla. Una parametrización útil en la práctica, que mejora la capacidad de aproximación de los modelos TSK, es la forma siguiente:

Con i = 1, …,N. Donde N es el número de reglas, x_i son las variables de entrada, y_i son las variables de salida locales, A_ij son conjuntos difusos caracterizados por las funciones de pertenencia mA_ij(x_i) y b_ij son escalares. Este modelo es conocido como modelo TSK afín, el cual es esencialmente una aproximación multi-modelo en la cual los modelos lineales simples se combinan para describir el comportamiento global del sistema. Esta propiedad facilita el análisis de los modelos TSK en un marco similar a la de los sistemas lineales.

Si la salida de un sistema difuso de este tipo aparece como una de sus entradas, se obtiene el llamado sistema difuso TSK dinámico. Este se construye a partir de las reglas tale como:

Donde u(k) es la entrada al sistema y x(k) = [x(k)…x(k-n+1)] es el vector de estado del mismo.

La salida del sistema difuso TSK es un promedio pesado de los valores de los consecuentes de las reglas, por lo que se simplifica el sistema. La fórmula de inferencia es:

Donde y es la salida del sistema, w_i es el nivel de impacto de la regla i que se define como:

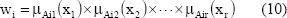
Lo cual se puede poner como:

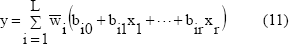
Donde;

Es el nivel de impacto normalizado. Sin embargo, la sencillez de estos modelos es lo que implica sus mayores problemas [33], los cuales son:

1) Al constituirse sus consecuentes en fórmulas matemáticas podrían no representar un marco natural para la reflejar el conocimiento.

2) No hay mucha libertad para aplicar diferentes principios de lógica borrosa por lo que se pierde versatilidad.

Su principal ventaja es que computacionalmente es muy eficiente, trabaja bien con técnicas lineales y con técnicas de optimización y adaptables, garantizan continuidad de la superficie de salida, etc.

2.2.3 Combinación del sistema TSK con las redes neuronales
Las redes neuronales, como paradigmas o modelos matemáticos simplificados de modelos semejantes al cerebro humano, funcionan como redes de computación de distribución paralela. Quizás la ventaja más importante de las redes neuronales es su adaptabilidad. Ellas pueden automáticamente ajustar sus parámetros (pesos) para optimizar comportamiento. La adaptación permite que puedan funcionar correctamente, aun cuando el ambiente o el sistema controlado varíe en el tiempo. Hay muchos problemas de identificación y control que pueden beneficiarse con una adaptación y modelación no lineal continua.

Mientras la lógica borrosa ejecuta un mecanismo de inferencia bajo conocimiento impreciso, las redes neuronales ofrecen ventajas excitantes tales como: aprendizaje, adaptación, tolerancia al fallo, paralelismo y generalización.

Aunque la lógica borrosa puede codificar el conocimiento del experto directamente, usando reglas con etiquetas lingüísticas, usualmente toma una gran cantidad de tiempo diseñar y sintonizar las funciones de pertenencia que definen cuantitativamente dichas etiquetas lingüísticas. Las técnicas de aprendizaje de las redes neuronales permiten automatizar este proceso y reducir sustancialmente el tiempo de desarrollo y el costo mientras que se mejora el rendimiento. De la combinación de ambas técnicas resultan los sistemas híbridos llamados sistemas neuro-difusos.

La arquitectura ANFIS (Adaptive Neural Fuzzy Inference Systems) (Jang, 1993) es un ejemplo de estos tipos de sistemas para el ajuste de los parámetros de un sistema difuso a partir de pares de datos de entrada-salida. Funcionalmente equivalente a un sistema borroso, el proceso de inferencia se implementa como una red neuronal que se ajusta por medio de técnicas de gradiente descenderte y mínimos cuadrados, y es capaz de ajustar los parámetros del antecedente y del consecuente.

ANFIS es un sistema neuro-difuso que combina las ventajas de los sistemas borrosos y de las redes neuronales. Como sistema difuso no requiere de un gran conjunto de datos y proporciona transparencia, suavidad y representación del conocimiento previo. Como una red neuronal, proporciona adaptabilidad paramétrica.

2.2.3.1 Arquitectura ANFIS
La Fig. 3 muestra un modelo difuso TSK de primer orden de dos reglas y dos entradas. Su arquitectura ANFIS equivalente se muestra en la Fig. 4.

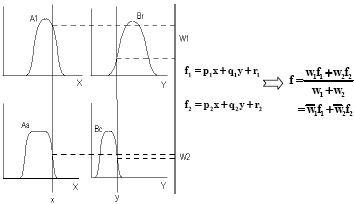
Figura 3. Modelo difuso TSK
Figure 3. Fuzzy model TSK.

Figura 4. Arquitectura de ANFIS.
Figure 4. ANFIS arquitecture.

Como se aprecia, la arquitectura presenta cinco capas.

Capa 1: Cada nodo calcula el grado de pertenencia (mA_i y mB_i), se implementan las funciones de pertenencia. Los parámetros de esta capa (parámetros de las funciones de pertenencia del antecedente) son conocidos como parámetros de premisa,por ejemplo, para el caso de una función de tipo Gauss estos parámetros serian c_i ys.

Capa 2: Cada nodo calcula el nivel de impacto de una regla:

Capa3: Calcula los niveles de impacto normalizados:

Capa 4: Calcula la salida de cada regla y la multiplica por el nivel de impacto normalizado correspondiente:

Los parámetros de cada capa (parámetros del polinomio del consecuente) son conocidos como parámetros del consecuente, para este caso serian r_i, p_i y q_i.

Capa 5: Calcula la salida total del sistema de inferencia difuso.

2.2.4 Obtención del modelo TSK para el RCTA
Para ello nos valemos de la herramienta fuzzy de MATLAB, específicamente el ambiente anfis cuyas características esenciales fueron descritas mas arriba. Se obtuvieron los datos experimentales de entrada salida del proceso formado por el vector: [flujo de reactivo, flujo de refrigerante, concentración] y como salida el vector de datos de concentración. Esta aparece como entrada porque se utiliza la forma dinámica del TSK. A partir de los mismos se elaboran los conjuntos de datos de entrenamiento y de chequeo del modelo del sistema de inferencia borroso.

La corrida simulada de experimentación se llevó a acabo durante 360 minutos, tomándose muestras de las entradas y salida simultáneamente cada 0.5 min.

Se formó el vector de entrenamiento tomando las muestras de la 101 a la 360 (261 en total) y las restantes 360 (de la 361 a la 720) se utilizaron para el chequeo del modelo. Mediante el ambiente anfis de MATLAB se obtuvo el sistema difuso del proceso cuyas principales características son:

CSTR_Fis =
name: 'CSTR_Fis'
type: 'sugeno'
andMethod: 'prod'
orMethod: 'probor'
defuzzMethod: 'wtaver'
impMethod: 'min'
aggMethod: 'max'
input: [1x2 struct]
output: [1x1 struct]
rule: [1x9 struct]
trndata: [261x3 double]
chkdata: [361x3 double]

El sistema de inferencia anterior consta de 9 reglas con funciones de membresía tipo campana de Gauss. El comportamiento del modelo (“*” en tono de grises) en relación a los datos de chequeo utilizados (“o” en tonos negros) se muestra en la Fig. 5. El error dinámico se indica en la Fig. 6 para el mismo conjunto de datos experimentales.

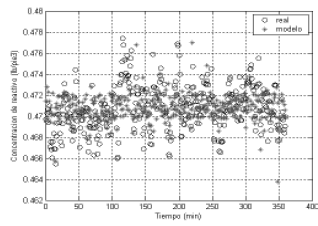
Figura 5. Comparación de concentración real (o negro) con el valor ofrecido por el modelo (* gris).
Figure 5. Comparison actual concentration (o negro) with model values (* grey) .

Figura 6. Error de predicción del modelo difuso en comparación con los datos reales de entrenamiento.
Figure 6. Prediction error of fuzzy model compared with training real data.

Como se puede apreciar, el modelo describe al proceso no lineal con un error de prueba máximo de 0.0022, lo cual pone en evidencia el carácter adecuado del mismo al proceso real.

Las funciones de pertenencia utilizadas en CSTR_Fis son del tipo campana de Gauss; pero con otros tipos, tales como la triangular, trapezoidal, etc. se obtuvieron errores de predicción totalmente satisfactorios también.

2.3 Identificación Del Sistema Por Métodos Convencionales
Con el objeto de comparar el modelo borroso presentado con alguna variante de modelo lineal determinado mediante técnicas clásicas, se procedió a encontrar algunas de estas. Para ello, la misma base de datos experimentales se utilizó para encontrar, cuál de las estructuras paramétricas clásicas lineales ARX, ARMAX, OE, BJ, etc. ofrecía las mejores opciones. Utilizando la herramienta ident de MATLAB. Se encontraron distintos modelos lineales que relacionan la salida C_a con los mandos F_i y F_c. Los mejores resultados en este caso se obtuvieron con las estructuras: variables de estado (n4s2) y auto regresivo con señal exógnea (ARX).

2.3.1 Modelo en variables de estado
El modelo discreto obtenido es de la forma:

Donde; T es periodo de muestreo.

Mediante MATLAB se obtuvo los siguientes valores para las matrices A, B, C, D y K:

El desempeño del modelo comparado con los datos reales se observa en la Fig. 7. En este caso resultó un 41% de fijación del modelo a los datos reales, lo cual no se considera favorable.

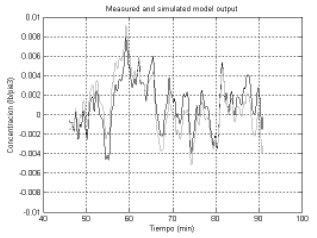
Figura 7. Comparación de datos reales (negro) con datos del modelo en variables de estado (grises).
Figure 7. Comparison of real dates (black) with state variable model (grey).

2.3.2 Modelo ARX
En este caso el mejor modelo resultó un arxqs de la forma:

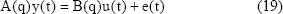
Resultando los polinomios en el operador de retardo q siguientes:

El comportamiento de los valores de la salida predichos por este modelo se compara con los mismos valores reales que los anteriores en la Fig. 8.

Figura 8. Comparación de datos reales (negro) con datos del modelo en variables de estado (grises).
Figure 8. Comparison of real dates (black) with ARX model (grey).

Este modelo se comporta un tanto mejor que el anterior, pues se logra un 77% de fijación a los datos reales, aunque no se puede considerar tampoco un buen modelo. Con ninguno de los dos se obtienen valores promedio del error de predicción menores que el logrado con el sistema de inferencia borroso desarrollado.

 

3. CONCLUSIONES

En el trabajo se resalta la importancia y se pone en evidenciada las posibilidades que tienen los modelos borrosos basados en la estructura TSK dinámica, en cuanto a precisión y exactitud, en la predicción del comportamiento de un proceso de dinámica compleja como es el caso de RCTA y cuyas características son, además, fuertemente no lineales.

El trabajo constituye la base para el desarrollo posterior de un predictor no lineal del proceso con vistas al diseño de un controlador predictivo no-lineal del sistema mediante modelos locales lineales en la trayectoria.

 

REFERENCIAS

[1] ABONYI J. Fuzzy Model Identification for Control, Birkhauser Boston, MA, USA . 2003         [ Links ]
[2] ANGELOV P, FILEV D, KASABOV N. and CORDON O. Evolving fuzzy systems, Memorias de 2nd International Symposium on Evolving Fuzzy Systems, pp 7-9. 2006.         [ Links ]
[3] ANGELOV P. y KASABOV N. Evolving Intelligent Systems, eIS. IEEE SMC eNews Letter, 2006 pp. 1-13.         [ Links ]
[4] ANGELOV P.P. y FILEV D.P. An approach to online identification of Takagi-Sugeno fuzzy models. IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics, Vol. 34, No. 1, 2004, pp 484-498.         [ Links ]
[5] BABUSKA R. Fuzzy Modeling for control, Vol.I, Kluwer Academic Publisher, Boston , 1998.         [ Links ]
[6] DÍEZ J.L. Técnicas de agrupamiento para identificación y control por modelos locales. Tesis Doctoral, Universidad Politécnica de Valencia, Valencia , España. 2003.         [ Links ]
[7] KASABOV N.K. Adaptation and interaction in dynamical systems: Modelling and rule discovery through evolving connectionist systems. Applied Soft Computing, Vol. 6 , No. 3, 2006, pp. 307-322.         [ Links ]
[8] KASABOV N.K. and SONG Q. DENFIS: dynamic evolving neural-fuzzy inference system and its application for time-series prediction. IEEE Transactions on Fuzzy Systems, Vol. 10, No. 2, 2002, pp. 144-154.         [ Links ]
[9] LUGHOFER E. Data-Driven Incremental Learning of Takagi-Sugeno Fuzzy Models, Tesis Doctoral, University Linz, Austria. 2005.         [ Links ]
[10] MARTÍNEZ B.L, FERNÁNDEZ J, MARICHAL E .y HERRERA F. On line clustering methods and its applications in fuzzy modeling. Memorias del Simposio Internacional de Fuzzy y Conjuntos Rugosos, ISFUROS 2006, Santa Clara, Cuba, 2006.         [ Links ]
[11] MARTÍNEZ B.L. y MARICHAL E. Generación automática de modelos difusos Takagi-Sugeno a partir de dato”, Memorias del IX Congreso Internacional de Matemática y Ciencias de la Computación COMPUMAT 2005.         [ Links ]
[12] VERNIEUWE H, BAETS B.D. y VERHOEST N.E.C. Comparison of clustering algorithms in the identification of Takagi-Sugeno models: A hydrological case study. Fuzzy Sets and Systems, Vol. 157, No. 21, 2006, pp. 2876-2896.         [ Links ]
[13] CHIU L. y OTROS. Fuzzy Model IdentificationBased Cluster Estimation. Journal of Inteligent & Fuzzy systems, 2(3), 1994.
[14] BARANYI P, YAM Y, VARKONYI-KÓCZY A, PATTON R.J, MICHELBERGER P. y SUGIYAMA M. SVD Based Reduction to TS Fuzzy Models. IEEE Transaction on Industrial Electronics, Vol. 49, No. 2, 2002, pp. 433-443.         [ Links ]
[15] CHEN C.C. and WONG C.C. Significant fuzzy rules extraction by an SVD–QR-based approach. Cybernetics and Systems, Vol. 36, No. 6, 2005, pp. 597-622.         [ Links ]
[16] HERRERA F. y MARTÍNEZ B.L. Reducción de Complejidad en Modelos Difusos, Memorias de XI Congreso Latinoamericano de Control Automático, La Habana, Cuba. 2004.         [ Links ]
[17] TAKACS O. y VARKONYI-KOCZY A.R. SVD-based complexity reduction of rule-bases with nonlinearantecedent fuzzy sets. IEEE Transactions on Instrumentation and Measurement, Vol. 51, No. 2, 2002, pp. 217-221.         [ Links ]
[18] YEN J, WANG L. y GILLESPIE W. A global local learning algorithm for identifying Takagi_Sugeno_Kang Fuzzy ModeL. IEEE International Conference on Fyzzy Systems. Anchorage, Alaska, May 4-9, 1998.         [ Links ]
[19] KORTMANN y P. UNBEHAUEN H. Structure identification of functional-type fuzzy models with application to modeling nonlinear dynamic plants. In: Lectures notes on Computer Science 1226. Ed. Bernd Reusch: Computational Theory and Applications Internacional Conference, 5th Fuzzy Days.Dortmund, 1999.
[20] CORDÓN O, GOMIDE F, HERRERA F, HOFFMANN F. y OTROS. Ten years of genetic fuzzy systems: current framework and new trends. Fuzzy Sets and Systems, Vol. 141, No. 1, 2004, pp. 5-31.         [ Links ]
[21] REYES I. Modelación de un biorreactor usando técnicas neuro difusas, Tesis de Maestría, Universidad Central de Las Villas, Santa Clara, Cuba. 2005.         [ Links ]
[22] ESPINOSA J. y VANDELWALL J. Predictive Control Using Fuzzy Model, 3th On-Line World Conference on Soft Computing in Engineering and Manufacturing.         [ Links ]
[23] SU M.C, CHOU C.H, LAI E. y LEE J. A new approach to fuzzy classifier systems and its application in self-generating neuro-fuzzy systems. Neurocomputing, Vol. 69, No. 4-6, 2006, pp. 586-614.         [ Links ]
[24] WANG L.X. A course of fuzzy systems and control. Prentice Hall PTR, NJ, 1997.         [ Links ]
[25] SONG Z. y KUSIAK A. Constraint-Based Control of Boiler Efficiency. A Data-Mining Approach. IEEE Transaction on Industrial Informatics. Vol. 3, No 1, Feb 2007.         [ Links ]
[26] JANG J.S.R; ANFIS. Adaptive-network based fuzzy inference system. IEEE Transaction on Systems, Man and Cybernetics, 23, 665-685, 1993.         [ Links ]
[27] JANG J.S.R, SUN R. y MIZUTANI, C.T. Neuro-Fuzz and soft computing. Prentice Hall, may, N.J, 1997.         [ Links ]
[28] SUGENO M. y KANG G.T. Successive identification of fuzzy model. Fuzzy Sets and systems, 28 (1), 15-3, 1988.         [ Links ]
[29] TAKAGI T. y SUGENO M. Fuzzy idewntification of systems and it applications to modeling and control. IEEE Trans. On Systems, Man and Cybernetic, 15(1), 116 - 132, 1993.         [ Links ]
[30] ESPINOSA J, VANDEWALLE J. y WERTZ, V.Fuzzy Logic, Identification and Predictive Control. London. Springer, 2005.         [ Links ]
[31] ESAFEI A.L. y KARA Y.F. Variable-structure-based fuzzy-logic indentification of a class of nonlinear systems. Control Systems Technology. IEEE Transactions on Automatic Control. Vol. 13, Issue 4, July 2005, pags. 646-653.         [ Links ]
[32] RODRIGUEZ M. A.Control Predictivo de un Reactor Lineal con Restricciones, XI congreso Latinoamericano de control Automático, Informática-2004, Habana, Cuba. Mayo, 2004.         [ Links ]
[33] MARTINEZ B. Identificación Difusa de un Bioreactor. Tesis de Maestría en Ingeniería en Automática, Universidad Central de Las Villas, Cuba, 2000.         [ Links ]