ALGORITMO PARA EL ANÁLISIS PROBABILÍSTICO EN SISTEMAS DE DISTRIBUCIÓN CON GENERACIÓN DISTRIBUÍDA

ALGORITHM FOR PROBABILISTIC ANALYSIS OF DISTRIBUTION SYSTEMS WITH DISTRIBUTED GENERATION

 

CESAR AUGUSTO PEÑUELA MENESES
Dr. (c), Universidad Estadual Paulista UNESP, Brazil, cesar_penuela@hotmail.com.

MAURICIO GRANADA ECHEVERRI
Ph.D, Profesor Asociado, Universidad Tecnológica de Pereira, magra@utp.edu.co.

JOSÉ ROBERTO SANCHES MANTOVANI
Ph.D, Universidad Estadual Paulista UNESP, Brazil, mant@dee.feis.unesp.br

 

Recibido para revisar Noviembre 24 de 2010, aceptado Junio 7 de 2011, versión final Julio 27 de 2011

 

---

RESUMEN: Este artículo presenta un algoritmo eficiente para el análisis probabilístico de sistemas de distribución trifásicos desbalanceados con conexión de generadores distribuidos (sistemas levemente enmallados). Este algoritmo hace uso de la técnica del Método Estimado de Dos Puntos para el cálculo del comportamiento probabilístico de las variables aleatorias del sistema. Adicionalmente, y con el fin de explotar eficientemente las características topológicas de la red, el análisis determinístico de las variables de estado es realizado por medio de un Flujo de carga Radial Basado en Compensación (FCRBC). Para el tratamiento de la generación distribuida, se propone una estrategia para incorporar dentro del FCRBC un modelo simplificado del generador junto con un control de las variables de despacho en el punto de conexión con la red. De este modo, el nodo con generación distribuida puede ser modelado como un nodo PV, o nodo PQ, dependiendo del modo de control y de las condiciones operativas del generador. Para validar la eficiencia del algoritmo propuesto es usado el sistema de prueba IEEE de 37 nodos. Los resultados probabilísticos son comparados con los obtenidos usando el método de Monte Carlo.

PALABRAS CLAVE: Flujo de carga, sistemas trifásicos, distribución, probabilístico, levemente enmallados, generación distribuida.

ABSTRACT: In this paper an efficient algorithm for probabilistic analysis of unbalanced three-phase weakly-meshed distribution systems is presented. This algorithm uses the technique of Two-Point Estimate Method for calculating the probabilistic behavior of the system random variables. Additionally, the deterministic analysis of the state variables is performed by means of a Compensation-Based Radial Load Flow (CBRLF). Such load flow efficiently exploits the topological characteristics of the network. To deal with distributed generation, a strategy to incorporate a simplified model of a generator in the CBRLF is proposed. Thus, depending on the type of control and generator operation conditions, the node with distributed generation can be modeled either as a PV or PQ node. To validate the efficiency of the proposed algorithm, the IEEE 37 bus test system is used. The probabilistic results are compared with those obtained using the Monte Carlo method.

KEYWORDS: Power flow, three-phase systems, distribution, probabilistic, weakly meshed systems, distributed generation.

---

 

1. INTRODUCCIÓN

Tradicionalmente, los sistemas de distribución han sido considerados como redes pasivas con topología radial. Sin embargo, buscando mejorar la eficiencia de la matriz energética, es posible actualmente incorporar pequeñas fuentes de generación cerca de los centros de consumo. Este tipo de generación modifica la forma tradicional en que las redes de distribución son operadas y proyectadas y origina lo que se conoce como Generación Distribuida (GenDis).

Algunos estudios [1],[2] muestran que la GenDis produce impactos positivos cuando es conectada a la red, tales como; la reducción en pérdidas de potencia y mejoramiento de los índices de confiabilidad y perfiles de tensión del sistema,. Por otro lado, en [2],[3] se muestran posibles problemas técnicos, tales como; el incremento en las corrientes de corto circuito y la pérdida de selectividad en el sistema de protecciones, que dificultan la operación de los Generadores Distribuidos (GDs). Así, para determinar la factibilidad de la conexión de nuevas fuentes de GenDis en la red o la adecuada operación de los GDs instalados en la red, se hace necesario el uso de herramientas computacionales suficientemente robustas y eficientes que permitan conocer las variables de estado de la red bajo cualquier escenario.

Las herramientas tradicionales de flujo de carga permiten calcular el punto de operación del sistema eléctrico de potencia en estado estacionario. Sin embargo, generalmente estas herramientas no consideran la naturaleza incierta inherente en los sistemas eléctricos, especialmente en lo que concierne al comportamiento de la demanda y a las fuentes de generación.

En este artículo se presenta un algoritmo eficiente para el análisis probabilístico de variables con incertidumbre. En este caso, se considera la estocacidad en el valor de la demanda y el impacto que se genera en los GDs conectados a los sistemas de distribución trifásicos, tanto balanceados como desbalanceados. Sin embargo, el algoritmo es suficientemente robusto para considerar incertidumbre en cualquier elemento o variable del sistema y, además, es capaz de manipular los diferentes tipos de funciones de distribución de probabilidad que pueden definir el comportamiento aleatorio de una variable [4].

El algoritmo propuesto incorpora un caso especial del método de estimación de puntos, usado en el análisis probabilístico, conocido como Método Estimado de Dos-Puntos (MDP), en vez del tradicional algoritmo basado en Simulación de Monte Carlo (SMC). La principal característica del MDP es que sólo requiere calcular dos flujos de carga por cada una de las variables aleatorias en estudio. Esta característica torna el MDP un algoritmo altamente eficiente en comparación con la SMC. Por otro lado, cualquier análisis probabilístico requiere del cálculo de múltiples puntos de operación, es decir, requiere evaluar diferente escenarios con alguna probabilidad de ocurrencia. Por tal motivo, es necesario contar con una herramienta robusta y eficiente para el cálculo del Flujo de Carga en sistemas trifásicos desbalanceados.

En este artículo se propone una modificación al método iterativo de Flujo de Carga Radial Basado en Compensación (FCRBC) [5], el cual explota en forma eficiente la topología levemente enmallada de los actuales sistemas de distribución. Las modificaciones al FCRBC mejoran su eficiencia computacional y afectan: i) el modelo matemático de los generadores, y ii) el número de barridos iterativos necesarios para la convergencia del algoritmo.

 

2. REVISIÓN BIBLIOGRÁFICA

Gran parte de los estudios de flujo de carga, aplicados a los sistemas de distribución, son basados en la técnica de barrido iterativo [6]. Esta técnica se caracteriza principalmente por ser eficiente computacionalmente y por permitir la adición de forma fácil y directa de diferentes modelos matemáticos, que representan el comportamiento de los dispositivos eléctricos del sistema. La idea central de estos algoritmos es aprovechar la característica radial de los sistemas de distribución para resolver un conjunto de ecuaciones algebraicas en forma eficiente y ordenada. Adicionalmente, usando la técnica de compensación [7], el Flujo de Carga Radial (FCR) puede ser aplicado en la solución de sistemas levemente enmallados, tal como se propone en [5]. En este FCR es utilizado un modelo simplificado del generador basado en fuentes equilibradas de tensión. En este caso, es despreciado el efecto que se genera sobre las componentes de secuencia negativa y cero en caso de condiciones de desequilibrios en terminales de la máquina.

El FCR propuesto [5], puede ser descrito como un proceso iterativo conformado por los dos pasos siguientes: i) cálculo de un flujo de carga radial, y ii) corrección de inyecciones de corriente en los puntos de quiebre. En el primer paso, la red levemente enmallada (Figura 1) es transformada en un equivalente radial (Figura 2) por medio de la inyección de corrientes en puntos de la red conocidos como puntos de quiebre. Estos puntos se caracterizan por formar trayectorias cerradas en la red (GDs, mallas, cortos-circuitos) y son denotados como B1 y B2 en la Figura 1.

Figura 1. Red levemente enmallada

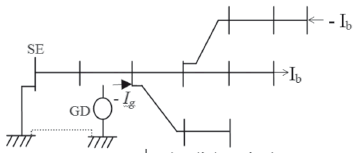
Figura 2. Red radial equivalente

En el segundo paso, se ajustan las corriente en los puntos de quiebre de modo que las condiciones del sistema original sean satisfechas. Para tal efecto se utiliza (1), donde [Z] es la matriz de sensibilidades formada por los equivalentes de Thévenin de los puntos de quiebre. Su construcción es ampliamente discutida en [6], [8].

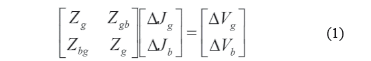
En forma compacta, esta ecuación puede ser descrita como:

Con respecto al problema de Flujo de Carga Probabilístico (FCP), para el análisis de variables aleatorias de los sistemas de potencia, las propuestas iniciales pueden ser referenciadas en [9].

En un FCP, las variables inciertas de entrada son caracterizadas por Funciones de Densidad de Probabilidad (FDP) o por Funciones de Densidad Acumulada (FDA). Consecuentemente, en respuesta se obtiene el comportamiento probabilístico de variables inciertas de salida, descrito también por FDP o FDA. Estas variables de salida pueden ser: flujos de potencia, generaciones, pérdidas, tensiones y ángulos, entre otras. El FCP puede resolverse numéricamente usando SMC, métodos aproximados, métodos analíticos, o una combinación de los anteriores.

La SMC [10], en cada iteración, genera valores aleatorios de las variables inciertas y resuelve un Flujo de Carga Determinístico (FCD) para construir, iterativamente, el comportamiento probabilístico de las variables de salida. Su gran limitación por tanto, es el alto esfuerzo computacional que supone generar un gran número de estados y resolver su respectivo FCD.

Los métodos aproximados, de los cuales hace parte el MDP, proveen una descripción con razonable exactitud, de las propiedades estadísticas de las variables de salida. El MDP fue desarrollado por Rosenblueth [11], y es usado para el cálculo de momentos estadísticos de una cantidad aleatoria que es función de una o más variables aleatorias.

 

3. FCRBC MEJORADO

En esta sección se presentan las modificaciones realizadas al algoritmo de Flujo de Carga Radial Basado en Compensación (FCRBC) presentado en [7]. Estas modificaciones buscan mejorar el desempeño computacional, modificando la estructura del algoritmo, y mejorar el modelo matemático de los generadores distribuidos permitiendo el control de las condiciones operativas del generador.

A. Estructura del Algoritmo
La Figura 2a muestra un diagrama de flujo generalizado del algoritmo tradicional propuesto en [12]. En este algoritmo el método de suma de corrientes es usado para el cálculo de Flujo de Carga Radial (FCR). Cuando el flujo alcanza convergencia, se inicia la aplicación del método de compensación. Por tanto, la convergencia global del algoritmo se alcanza cuando los criterios del FCR y del método de compensación son satisfechos. En la Figura 2b se presenta el algoritmo propuesto, en el cual el procedimiento de compensación es realizado después de cada actualización de las tensiones, dentro del algoritmo de barrido iterativo. Las pruebas realizadas han mostrado una reducción importante en el número de barridos iterativos requeridos para la convergencia global por medio de la aplicación del algoritmo propuesto.

Figura 3. Comparación entre Diagramas de Flujo

B. Modelo Matemático del Generador
En estudios de flujo de potencia los GDs deben ser modelados de acuerdo al tipo de fuente y conexión al sistema de potencia [13]. En este artículo, el modelo adoptado corresponde a la formulación matemática con representación en fase, descrita en [14], para la máquina síncrona, el cual es ilustrado en forma simplificada en la figura 4.

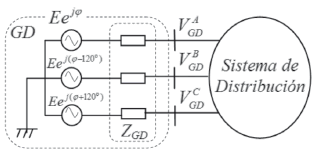
Figura 4. Modelo Matemático para GD.

Este modelo permite el control de las condiciones operativas del generador, tales como el control de la corriente de armadura y flujo de potencia en el punto de conexión con el sistema de distribución. Los parámetros necesarios para el cálculo de la matriz ZGD generalmente son informados por los fabricantes en forma de impedancias de secuencias (X0, X1, X2), de tal forma que la ecuación (3) puede ser usada.

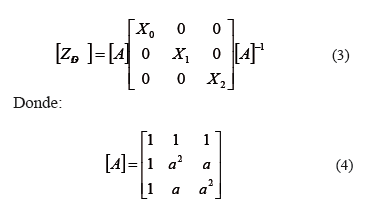
El operador a representa el desfase 120º y su valor es 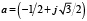. La estrategia propuesta para resolver un flujo de carga que considere el modelo matemático del GD presentado, consiste en aplicar el método de compensación para encontrar las corrientes por fase del generador, , y el nivel de tensión interna E, necesarias para proveer las condiciones de despacho en terminales del GD. Es decir, el generador debe entregar una potencia activa, Pesp, y reactiva Qesp, en caso de un control con factor de potencia constante, o de lo contrario entregar una potencia activa, Pesp, y una tensión en terminales del generador, Vesp, en caso de un control del nivel de tensión. La ecuación (5) relaciona la tensión de generación interna, 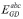, en función de las tensiones en terminales de cada fase del generador 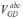, y sus respectivas corrientes .

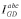Por otro lado, la tensión interna necesaria para mantener las condiciones de despacho del generador puede ser modelada a partir del circuito de secuencia positiva, tal como se muestra en la ecuación (6), donde 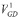es la componente de secuencia positiva de la tensión en terminales,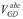

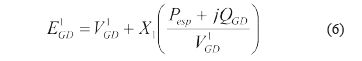
Si el modo de control del GD es de factor de potencia constante, QGD es igual a la potencia especificada (QGD=Qesp). En caso contrario, la potencia reactiva debe ser ajustada iterativamente para determinar la cantidad de reactivos necesarios para mantener el nivel de tensión en terminales del GD. Para tal efecto, la ecuación (7) es usada para encontrar el valor estimado, donde [X] es una matriz de sensibilidad, similar a la mostrada en la ecuación (1), que contiene sólo reactancias de secuencia positiva [6].

Luego de resolver el sistema (7), la nueva potencia reactiva inyectada por el GD es dada por:

La diferencia de tensión ΔVg de la ecuación (1) es calculada por medio de la ecuación (9). Los deltas de tensión en los demás tipos de puntos de quiebre son calculados tal como se presenta en [13].

Las condiciones de operación del GD pueden ser controladas para mantener la máquina dentro de la zona de operación factible. La tensión de generación se encuentra directamente ligada a la corriente de excitación, por tanto, al aplicar la restricción (10) se puede prevenir sobrecalentamiento del devanado de campo.

Para prevenir el sobrecalentamiento de los devanados de armadura, pueden ser impuestos límites a la corriente de armadura, la cual se encuentra ligada a las condiciones de despacho del generador en la ecuación (11).

Si la potencia reactiva alcanza un límite operacional, el valor de la potencia reactiva es fijado en el límite y el control del generador se mantiene en modo de factor de potencia constante.

 

4. MÉTODO DE DOS-PUNTOS PARA ANÁLISIS PROBABILISTICO.

El cálculo de las variables de estado de un sistema eléctrico de potencia, operando en régimen permanente, es obtenido a través de métodos tradicionales de flujo de potencia. A partir de ese punto de operación es posible conocer otras variables de interés, Z, tales como flujos de corriente por las líneas y pérdidas de potencia activa y reactiva. Sin embargo, los parámetros de entrada al flujo de carga, W, pueden, en casos más próximos a la realidad, poseer comportamientos aleatorios en n elementos. Bajo esta situación, W es caracterizada por una función de densidad de probabilidad fW(w), un valor medio mW y una desviación estándar σW. Así, Z es también una cantidad aleatoria en función de W, es decir Z=h(W). Dadas las características de los sistemas eléctricos, la función h(W) contiene un comportamiento no lineal que debe ser aproximado mediante series de Taylor alrededor del punto de interés, mW.

Cada una de las m concentraciones de las variables Z, son definidas a través de sus posiciones wj y su probabilidad pj, (j=1,2,...,m) [15]. Así, el valor aproximado para el valor medio, mZ, usando m concentraciones de probabilidad, es dada por:

La posición wj es calculada por medio de la ecuación (14), donde εj es un parámetro a ser determinado.

Para el cálculo de las variables wj y pj de cada concentración m, la idea básica es obtener el momento estadístico mZ usando dos tipos diferentes de aproximaciones. La primera de ellas usa la definición de valor esperado de h(W), E(h(w)):

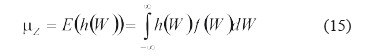
Usando (12) y (15) se obtiene:

Donde Mi(W) es el momento central de W, definido como:

La razón λWi=Mi(W)/σiW (i=1,2,...) permite encontrar factores ampliamente utilizados en el análisis probabilístico de variables aleatorias, tales como, el coeficiente de asimetría (skewness) y el coeficiente de aplanamiento (kurtosis). Así, la ecuación (16) puede ser rescrita, en función de estos factores:

donde λW,1=0, λW,1=1, λW,3 es el coeficiente de skewness, y λW,4 el coeficiente de kurtosis. De este modo, la ecuación (18) permite encontrar los momentos no cruzados de cada variable aleatoria W.

La segunda aproximación consiste en calcular mZ a partir de la ecuación (13), donde se pueden calcular los primeros momentos cruzados de cada variable aleatoria W. Sustituyendo (12) y (14) en (13), se obtiene:

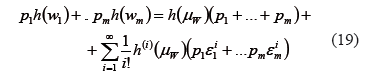
Al comparar los términos de la ecuación (18) y (19), es posible general el siguiente sistema de ecuaciones:

Para el esquema de Dos-Puntos (m=2), el sistema (20) es reducido a un conjunto de cuatro ecuaciones con cuatro incógnitas, (p1,p2,ε1,ε1). Las posiciones de las dos concentraciones, w1 y w2, son determinadas por medio de la ecuación (14), mientras que la aproximación del momento estadístico se realiza por medio de la ecuación (13). Para el caso del método de Dos-Puntos, la aproximación es de tercer orden, y por tanto, la solución es exacta cuando h(W) es una función polinomial de tercer orden.

Para concluir, y considerando la existencia de múltiples variables aleatorias, Wk, no-correlacionadas entre sí, dentro de un espacio n-dimensional W, caracterizadas por una desviación estándar σk y un valor esperado mk, la ecuación (20) puede ser expresada como:

Dado que la suma de todas las concentraciones debe ser igual a uno, se tiene:

Los sistemas (21) y (22), forman un conjunto de ecuaciones con 2m incógnitas por cada variable aleatoria. Luego, y dado que m=2, el sistema de ecuaciones queda determinado por:

 

5. ALGORITMO PROPUESTO PARA EL FLUJO DE CARGA PROBABILÍSTICO

La figura 5 muestra el diagrama de flujo del algoritmo propuesto. En el paso 1 del algoritmo se definen las condiciones iniciales y se identifican las variables aleatorias, almacenando sus índices dentro del vector UP. El tamaño del vector Z es definido por el número de variables aleatorias de interés. En el paso 2 se verifica el cálculo de las concentraciones máximas de cada variable aleatoria. En el paso 3, es seleccionada aleatoriamente una de las variables almacenadas dentro del vector UP, y sus concentraciones máximas calculadas en el paso 4. En el paso 6 se ejecuta el Flujo de Carga Radial, tomando como entrada, las alteraciones realizadas al valor la variable aleatoria en el paso 5. Los parámetros de salida son calculados y almacenados en el paso 7, los cuales, a su vez, permiten el cálculo de los valores estimados de la desviación estándar y del promedio.

Figura 5. Algoritmo propuesto para el FCP.

 

6. RESULTADOS NUMÉRICOS

Para mostrar la eficiencia de la metodología propuesta, es usado el sistema IEEE 37 nodos cuyos datos de red pueden ser consultados en [16]. El algoritmo fue totalmente implementado en la plataforma de desarrollo de software Delphi 7.0 y las simulaciones fueron ejecutadas en un computador con Intel Duo 2.3 GHz, y 3GB de RAM.

La topología del sistema original es ligeramente modificada con el fin de resaltar las características del algoritmo propuesto. De este modo, se considera retirar el regulador de tensión, incorporar el generador descrito en la Tabla 1, y adicionar una línea entre los nodos 718 y 725, la cual, posee las características constructivas de la línea existente entre los nodos 706 y 725. Esta línea adicional crea una malla en el circuito de distribución.

Tabla 1. Datos del Generador Distribuido.

Inicialmente se desea que el generador opere en condiciones nominales de potencia activa y reactiva (control de factor de potencia constante), y se ejecuta un flujo de carga determinístico usando el FCRBC mejorado (no existen variables aleatorias). El informe de resultados en el GD es presentado en la Tabla 2. En este caso, el control impuesto al generador reduce la cantidad de reactivos inyectados a la red con el fin de mantener la corriente de salida en torno al valor nominal (49A).

Tabla 2. Resultados para el GD.

Posteriormente, se determina un comportamiento aleatorio en el valor de la demanda de cada uno de los nodos de carga del sistema. Se considera una distribución normal en la potencia activa y reactiva, cuyos valores medios son los dispuestos en la base de datos del sistema original, mientras que los valores de las desviaciones estándar son asignados arbitrariamente entre el intervalo del 2% al 5%. Como variable de interés se asume la potencia activa y reactiva en el punto de conexión del GD. Sin embargo, en general, cualquier otra variable del sistema puede ser considerada [17].

Las FDA por fase, resultado de la aplicación del método propuesto y de la SMC, son comparadas en la Figura 6. Estas funciones muestran el comportamiento probabilístico, en el punto de conexión del GD, de la potencia activa (Figuras 6a, 6b y 6c) y reactiva (Figuras 6d, 6e y 6f), en cada una de las fases a, b y c, respectivamente.

Figura 6. Comparación de las FDAs obtenidas usando SMC y MDP.

Para la SMC se consideraron 9000 muestras, y el resultado obtenido se asume como el comportamiento probabilístico real a ser encontrado [10]. En este sentido, es de notar que el MDP logró determinar completa y adecuadamente el comportamiento probabilístico del GD (valor medio, desviación estándar y el tipo de distribución). El máximo error en la desviación estándar, con respecto a los resultados obtenidos por SMC, es de 2% en la potencia reactiva de la fase b del GD (ver Figura 6e). Para mostrar las ventajas computacionales del método propuesto, las siguientes estrategias fueron implementadas:

1. Estrategia 1 (E1): utilizar SMC y un Algoritmo Tradicional (AT) para análisis de flujos de potencia en sistemas levemente enmallados [6],[13];
2. Estrategia 2 (E2): utilizar el método de SMC y el FCRBC mejorado;
3. Estrategia 3 (E3): utilizar el MDP y el AT;
4. Estrategia 4 (E4): utilizar el MDP y el FCRBC mejorado.

En las estrategias anteriormente mencionadas, el algoritmo tradicional para el cálculo de Flujo de Carga Radial corresponde al ilustrado en la figura 3.a, el cual es ampliamente descrito en [5a],[13]. El tiempo computacional consumido por cada estrategia para resolver el flujo de carga probabilístico, se encuentra ilustrado en la Tabla 3. En tiempo de cálculo, la estrategia propuesta en este trabajo (E4) resulta ampliamente atractiva en comparación con las otras estrategias.

Tabla 3. Tiempo computacional (milisegundos)

 

7. CONCLUSIONES

Es presentado un algoritmo eficiente y robusto para resolver problemas de Flujo de Carga Probabilístico en sistemas de Distribución. Su estructura reúne las mejores características de dos metodologías conocidas en la literatura especializada: El flujo de Carga Radial basado en compensación, y el método de punto estimado de Dos-Puntos.

El primer método ofrece una manera eficiente de resolver flujos de carga en sistemas de distribución desbalanceados y topologías ligeramente diferentes a la radial. El esfuerzo computacional de esta metodología es mejorado y adicionalmente se desarrolla una estrategia para considerar la operación de la generación distribuida, así como de su tipo de control. El modelo propuesto no representa exactamente el comportamiento real de las máquinas de generación, ya que considera apenas los parámetros de mayor impacto en la operación en régimen permanente. Sin embargo, la estrategia puede ser extendida a modelos más completos, o aún, a modelos que representen el comportamiento de generadores en base a máquinas de inducción o fuentes con interfaz electrónica.

 

REFERENCIAS

[1] Gatta, F. M., Iliceto, F., Lauria, S. and Masato, P., Modeling and computer simulation of dispersed generation in distribution networks. measures to prevent disconnection during system disturbance, Bologna Power Tech Conference, Bologna, Italy, 2003.         [ Links ]
[2] Falaghi, H. and Haghifam, M.-R., Distributed generation impacts on electric distribution systems reliability: Sensitivity analyasis, Eurocon 2005. Serbia & Montenegro, Belgrade, 2005.         [ Links ]
[3] Chen, T. H., Chen, M. S., Lee, W. J., Kotas, P. and Olinda, P. V., Distribution system short circuit analysis. a rigid approach, IEEE Trans on Power System, vol. 7, no. 1, pp. 444-450, 1992.         [ Links ]
[4] Morales, J. M., and Prez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow, IEEE Trans on Power System, vol. 22, no. 4, pp. 1594-1601, 2007.         [ Links ]
[5] Shirmohammadi, H., Hong, W., Semlyen, A. and Luo, G. X., A compensation-based power flow method for weakly meshed distribution and transmission networks, IEEE Trans on Power System, vol. 3, pp. 753-762, 1988.         [ Links ]
[6] Shirmohammadi, and Cheng, C. S., A three-phase power flow method for real time distribution system analysis, IEEE Trans on Power System, vol. 10, no. 2, pp. 671-679, 1995.         [ Links ]
[7] Tinney, W. F., Compensation methods for network solutions by triangular factorization, Proc of PICA conference, Boston, Mass., 1971.         [ Links ]
[8] Moghaddas-Tafreshi, S. and Mashhour, E., Distributed generation modeling for power flow studies and trhee-phase unbalanced power flow solution for radial distribution systems considering distributed generation, Electric Power Systems Research, vol. 79, pp. 680-686, 2009.         [ Links ]
[9] Borkowska, B., Probabilistic load flow, IEEE Trans. Power Apparatus and Systems, vol. PAS-93, no. 3, pp. 752-755, 1974.         [ Links ]
[10] Rubinstein, R.Y., Simulation of the Monte Carlo Method. New York: Wiley, 1981.         [ Links ]
[11] Rosenblueth, Point estimation for probability moments, Proc. Nat. Acad. Sci. U.S.A., vol. 72, pp. 3812-3814, 1975.         [ Links ]
[12] Zhang, X., Soud, F., Shirmohammadi, D. and Cheng, C. S., A distribution short circuit analysis approach using hybrid compensations method, IEEE Trans on Power System, vol. 10, no. 4, pp. 2053-2059, 1995.         [ Links ]
[13] Kosterev, d., Modelling synchronous voltage sources converters in transmission system planning studies IEEE Trans on Power System, vol. 12, no. 12, pp. 947-952, 1997.         [ Links ]
[14] Acha, E., Claudio, R. Fuerte E., Ambriz, H., Perez, C. and Camacho, A., FACTs, Modelling and simulation in Power Networks, Chichester; Hoboken, NJ: John Wiley&Sons Ltda. England, pp 82-86, 2004.         [ Links ]
[15] Hong, H. P., An efficient point estimate method for probabilistic analysis, Reliability Engineering and System Safety, vol. 59, pp. 261-267, 1998.         [ Links ]
[16] Kersting, W. H., Radial distribution test feeders., IEEE Trans on Power System, vol. 6, no. 3, pp. 975-985, 1991.         [ Links ]
[17] Su, C.-L., Probabilistic load-flow computation using point estimate method, IEEE Trans on Power System, vol. 20, no. 4, pp. 1843-1851, 2005.         [ Links ]