1. Introduction
In the machining process, several variables are influenced by the process conditions [1-2], but only some variables are useful for the monitoring process and can be measured with sensors installed close to the machining tool zone [3]. The variable that can be considered having more relevance is the cutting force, because it is directly related to several performance characteristics and optimization [4]. For example, a determined cutting condition can be observed and the cutting parameters can be adjusted. In such a way, better cutting force efficiency can be obtained and therefore allows extending the tools life time, improving the quality of the machined parts, and contributing to a reduction of the machining costs [5-7].
The tool condition is an important factor to the precision of the machining process [8-9]. The tool wear is highly influenced by the machining force [10-11], so the higher the actuating forces on the cutting tool, the higher the tool wear [12]. The cutting force measurement can be used as an indication of change of the tool related to the progressive wear and prevention of the tool´s disruption in a conventional turning process [9]. Experimental results reported in [13], shows that the gradual growth of flank wear, the rapid cutting edge deterioration and catastrophic failure of the cutting tool, can be detected by using cutting force monitoring.
It is well known that during the machining process, the machining tool wears out, and in turn can increase the cutting force of the cutting tool. Therfore, there is important to look for a mechanism that will better be able to monitor the relevant variables in the machining process in real time, specifically the cutting force variable. Real time monitoring of the cutting force is the best solution [14].
In a real situation, there does not exist any theory related to workpiece machining that can be considered well suited enough, so that the cutting force can be easily predicted. What we have normally is a set of empiric formulations involving a set of constants which are not rapidly available, and also a dependency on several factors which demand a huge amount of data [15].
The turning process shown in Fig. 1 is a machining operation where a mechanical workpiece is fixed in the plate of a lathe and is rotated while the turning tool, fixed in a tool holder moves in a (x, z) plane that ideally contains the rotation axis of the machined workpiece [16]. This motion produces the machining force which is defined as the applied force by the mechanical workpiece to the cutting tool. This is the variable we are interested in to do the monitoring. The turning process described in Fig. 1 is characterized by three types of movements and five types of forces [16-18]:
Cut movement: It is characterized as the motion which creates only one chip removal.
Advance motion: It is characterized as the motion that promotes a repetitive or continuous lifting chip during several revolutions.
Effective cutting motion: It is characterized as the resulting motion due to cutting and advancing movements.
Fu: Machining force.
Ft (Active force): component of Fu localized in the working plane.
Fc (cutting force): projection of Fu on the cutting direction (given by the cutting speed).
Ff (advance force): Projection of Fu on the advance direction.
Fp (passive force): Component of Fu localized perpendicularly to the working plane.
Taking into account that few reports can be found about the cutting force in the threading process in a conventional lathe, this paper has the objective of doing the monitoring of the cutting force (Fc) in this kind of process, in real time. To do so, it was necessary to develop a data acquisition system based on LabView® programming.
In the research reported by Fredericks [19] and Teets [20], in the tools datasheets [21], and in many CNC programing manuals about the Thread cutting (TC) concerning the advance analyses methods of the tools into mechanical part direction, there are basically two strategies: One of them foresees constant cutting depth (CCD) (with the consequent cutting cross sections areas being variables) as can be seen in Fig. 2a, and the second strategy considering variable cutting depths (VCD) with cutting cross sections constants. This can be seen in Fig. 2b.
Usually, developers follow the tools manufacture’s recommendations that guide the user through tables obtained empirically to the VCD strategy, giving the necessary geometrical input parameters to the CNC machine program.
In the proposed methodology there will be a description of the analytical models that consider the advance strategy with variable depth of cutting.
2. Materials and methodology
2.1. Materials
In the setup of the experiments there were used three proof samples that were configured as shown in Fig. 3. In this figure there are shown the dimensions used in these samples. Samples consist of ABNT steel 1045.
Fig. 4 shows the setup used. The support for the insert used was R166 OG-16VM01-002 manufactured by Sandvik company (Fig. 4(a)). Also used in the experiment was a mechanical lathe by Romi, model TORMAX 30 A, a tool holder adapted with the load cell, a weight indicator (type Siciliano SDS), and a computer with the LabView® software installed.
2.2. Methodology
Fig. 5 shows variables and parameters considered in the cutting force monitoring. The depth of the cutting parameter will be the only input variable. The rest of the parameters will be held constant. This parameter was chosen because it promotes a significant influence on the cutting force [22].
This parameter is calculated using different methods. Markedly, the Fredericks´s model [19], the Sandvik´s model [21], and Lira´s model [23]. All of them were used to find the radial advance of the tool to the machining of the cylindrical threads in a conventional lathe.
The input parameters that were held constant were defined according to: The total number of passes (each pass is related with the infeed of a sample into the lathe) that are made by the tools (six passes in this experiment), the total thread depth is 0.94 mm and the fillet tip radius of the insert 0,2 mm. Also considered, was a rotation of 900 rpm. The input parameter that is considered variable is defined by the models:
- Sandvik´s model [21]: In this model is used the depth of cutting and the number of passes, for determination of absolute radial advance according with eq.(1):
Where: Δapx is absolute radial advance (mm), ap is the depth of cutting (mm), nap is the effective number of passes and j is a parameter that has a 0,3 value in the first trial, and for the rest of the passes it is calculated accordingly with the next equation:
- Lira´s Model [23]: In this model, in the calculus of the absolute radial depth is considered the tool tip radius. Calculus is made accordingly with eq.(3):
Where R f is the tool tip radius, i is the current trial, N is the total number of passes, and h is the depth of the thread.
Fredericks´s model [19]: In this model, the radial depth is calculated according to eq.(4):
Where: n is the current pass and N is the number of passes.
Using the data obtained from the eqs. (1), (3) and (4) there was a graph constructed as shown in Fig. 6. It is inferred that the Fredericks algorithm is the one that presents the greatest initial radial advance as well as the greater variation of the incremental radial advance. The model proposed by Sandvik shows the smallest incremental radial advance variation. The mathematical model of Lira indicates an intermediate behavior.
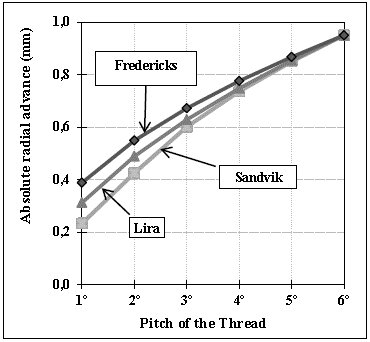
Source: The Authors.
Figure 6 Curves representing the data obtained for the absolute radial advance for each model considered in the respective pass.
With the data obtained by the eqs. (1), (3) and (4), there were obtained the values of the effective radial advance in each pass of each mathematical model as shown in Table 1.
2.3. LabView® data acquisition
The experimental setup is illustrated in Fig. 4. In that figure (part A), the load cell detects the analog signal of the cutting force and a weight indicator executes the conversion of the measured signal to the digital representation and exhibits the measured signal (part B of Fig. 4). This signal, in turn, is transmitted to the computer where data acquired from the weight indicator is processed and stored. Processing is done using an interface (program) developed in LabView® (part C in Fig. 4).
Fig. 7 shows a schematic of the setup used in the experiment to collect the data. This schematic is a simplified representation of Fig. 4. Part A in the figure corresponds with the load cell to acquire the analog signal. This signal goes into the weight indicator (part B) where there is a signal conditioning to obtain a digital signal. The digital signal goes via USB (part C) to the computer (part D). Finally, in the computer the data obtained is processed and stored using an application developed in LabView®.
Fig. 8(a) shows the main user interface in the LabView® Control panel. Using this interface, we developed the rest of the programming as shown in Fig. 8(b). As can be seen in Fig. 8(b), the programming was divided in six parts:
- A: In this part of the LabView® program the reading of the serial port is specified by the user and the preparation to recognize the termination character. This ending character also can be modified as necessary.
- B: In this block there is a processing of the reading of a specific number of bytes and the returning of the read data as a string.
- C: In this part of the programming is done the conversion of the read string into a numeric format. Also, completed in this block the counting and exhibition of the execution time.
- D: The number found in the previous item is converted into dynamic data as well as is done the association of this information with time.
- E: In this block it is implemented a graph and the data tabulation. As soon as the stop button is pressed the data in the table is sent to an Excel file.
- F: Correspond with the program completion or then causes the stopping of the program in case of an error in the serial port can be detected.
3. Results and discussions
In this experiment there were used three different mathematical models to determine the radial advancement of the tool to each pass. There were completed six passes for each model. The average data of the force that were obtained with the data acquisition system are shown in Fig. 9. This figure shows the average cutting force of each pass for each model considered. It can be seen that for each model, there is a different force profile with a different response as a function of the progression of passes.
In a machining process the cutting force increases proportionally with the incrementation of the cutting depth. But in the specific case of threading, the force variation during the passes is caused by the contact area variation of the cutting tool with the machined part. The greater the contact area, the greater is the resistance to the cutting tool advance, and therefore the greater is the force required to be applied to the machined part.
It can be inferred from Fig. 9:
- With Sandvik’s model there was a progressive increment of the cutting tool until the fifth pass. In the sixth pass, there was a minor force in comparison with fifth pass. This occurs due to the fact that in the fifth pass the thread was almost finished requiring a minor force. It was observed that the first and fifth passes are those having the minor and greater strength respectively between the models considered in these experiments. This model shows that the cutting force increases progressively and decreases in the last pass. The main problem observed in this model was that it exhibited a greater cutting force increment between the passes. A greater cutting force variation between the passes can cause a greater likelihood of catastrophic failure of the cutting tool.
- Lira’s model. Also was observed a progressive increment of the cutting force but only up to the fourth pass. For the remaining passes the cutting force decreased. This is due to the fact that after the fourth pass the thread was almost finished, and therefore, in the remaining two passes the cutting force required is minor. This model is very interesting compared to Sandvik’s model due to the cutting force increment between the passes was the minor observed with the models chosen to run the experiments.
- Fredericks’s model. Results with this model were somewhat different compared with previous models, showing the cutting force decreasing progressively along the passes. The model shows the minor maximum cutting force achieved in the first pass as well as the minor average cutting force of all models studied. The behavior observed with this model indicates that the cutting tool is exposed to a minor average cutting force when compared to the other models. It means that the cutting tool can have minor wear when this model is considered.
The knowledge about the threading process is very important as it allows us to minimize cost of the machining process. It is possible because allows predicting the cutting tools wear or failure probability and therefore avoiding the loss coming from unnecessary maintenance. As it is well known, usually it is adopted by the industry as a criterion of end of life of the cutting tool, the number of machined parts and safety factors guidelines. This approach can lead to additional machining costs. Also it would be possible avoid loss due to bad sizing of machines and tools, as it would otherwise be without a cutting tool force study, helping to estimate with enhanced precision the power required to specify the machines (lathes) and tools selection, as wells as a better sizing of fixing systems.
4. Conclusion
We presented here a system for data acquisition of the cutting force in mechanical lathes. The data acquisition system was implemented in LabView®. The results are as highlighted: The passes that have the higher average cutting force are: In the Sandvik´s model it occurs in the fifth trial (48.41 kgf). In Lira´s model, it occurs in the fourth trial (42.55 kgf). Finally, in Fredericks´s model, the higher cutting force occurs in the first trial (41.22 kgf). As can be expected, the passes that exhibited the highest cutting force values are the more critical passes, and are the ones with higher probability of catastrophic failure of the cutting tool.
Considering the average cutting force obtained with the three models (Sandvik, Lira and Fredericks models) the conclusion that can be drawn is that Sandvik´s model is the one having the highest cutting force variation between each trial (8.56 kgf) and a higher average cutting force of (36.45 kgf), and also having the passes with higher (48.41 kgf) and lower average cutting force (18.39 kgf). Therefore, such observed behavior can promote a bigger stress on the cutting tool which means a higher probability of failure of the cutting tool. In the case of Fredericks´s model, it was observed that it exhibit the lower average cutting force (33.99 kgf), and lower maximum peak of cutting force (41.22 kgf) taking place in the first trial. Lira´s model has an intermediate average cutting force (35.34 kgf) when compared with Sandvik and Fredericks models. This model exhibits the lower cutting force variations between passes (5.20 kgf).
This implemented data acquisition system allowed us to know, in real time, the intensity of the cutting force in conventional lathes. It allowed us to introduce machining strategies in such a way to preserve the cutting tool during the machining utilization, increasing its lifespan and allowing for obtaining products with the best quality. These experimental results can be useful as a manufacturing tool to predict the probability of failure of the cutting tool, and helping to reduce the cost of maintenance. Also important in this context is the possibility of having a mechanism that can help manufacturers to improve sizing of the machines and tools.




























