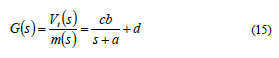1. Introducción
La región amazónica presenta gran potencial para utilizar la generación fotovoltaica, debido a un alto nivel de irradiancia en torno de 5000 a 5300 W/m2. En este sentido, las técnicas de control clásicas y avanzadas se utilizan para controlar la tensión de salida en el sistema autónomo. Muchos trabajos abogan por el uso de un sistema de control robusto, que tienen como propósito garantizar la estabilidad del sistema fotovoltaico autónomo y la seguridad del usuario para una banda de incertidumbres determinada (Jahangir, 2012), (Sahraoui, 2014) (Drid, 2014). Los trabajos de búsquedas en mejoras de la eficiencia en los convertidores son también una de las etapas del sistema, además de otras fuentes alternativas como: energía eólica, energía de gas natural, energía hidroeléctrica y energía solar (Pinto,2016).
Basado en la importancia de la energía solar para la comunidad, por ser limpia y silenciosa, el sentido de la investigación se ha dirigido, a partir de la aplicación de técnicas de control para para el buen desempeño de las variables de salida ante la presencia de perturbaciones como temperatura y sombreado, la teoría de control Fuzzy empleando el modelo Mamdani ha alcanzado las expectativas de rendimiento además, posibilitó la conexión a la red eléctrica del sistema fotovoltaico, creando a su vez la característica de generación distribuida y dando una nueva reconfiguración del sistema eléctrico de potencia, donde el consumidor pasa a tener la capacidad de generar localmente su propio consumo (Fernández, 2014).
Varios trabajos hacen uso de un proyecto de un control PI a través de metodologías de redes neuronales y técnicas de optimización (Saad, 2006) (Bastos, 2014). Otro trabajo que trata de metodologías avanzadas de proyectos de control aplicados en sistemas de distribución de energía se encuentra en (Yazdani, 2009), estos proyectos son basados en sistemas inteligentes de control. Ante estos precedentes de investigación, este trabajo presenta un análisis de la metodología en un ambiente estructurado bajo la plataforma Arduino, en el cual funciona un sistema fotovoltaico aislado controlado por un PI-Fuzzy.
Debido al alto costo de la instauración del sistema fotovoltaico, demostrado con el sistema autónomo en (Pinto, 2016), este trabajo pretende realizar el control y mejorar el desempeño del sistema, en un ambiente que no posea red eléctrica.
Este artículo está organizado de la siguiente manera: en la sección 2 se presenta el modelo matemático de un generador fotovoltaico; en la sección 3 se muestra el proyecto de un controlador PI-Fuzzy; en la sección 4 es presentada la metodología utilizada; en la sección 5 es presentado el análisis de los resultados obtenidos y por último, en la sección 6 se exhiben las consideraciones finales y las conclusiones del estudio desarrollado.
2. Modelo del generador fotovoltaico
2.1. Modelo matemático no lineal del modelo fotovoltaico
El modelo eléctrico equivalente del generador fotovoltaico presenta las pérdidas de voltaje y de corriente, que son las resistencias Rs y Rsh, respectivamente, de acuerdo con la Fig. 1. La resistencia en serie (Rs) representa las pérdidas de calor por efecto Joule que ocurren en las propias células a través de la resistencia eléctrica del material y de la resistencia de los contactos metálicos de la misma. La resistencia en paralelo (Rsh) proviene de las pérdidas acarreadas por corrientes parásitas que circulan en las células debido, principalmente, a las pequeñas imperfecciones en la estructura del material o impurezas (Ding, 2014) (Dyreson, 2014) (Lorent, 2014).
En un circuito ideal, las resistencias Rs y Rsh pueden ser despreciadas, sin embrago se utilizará el modelo de la Fig. 1. Así, la ecuación que expresa la corriente entregada (I pv ) en la carga será dada por las Ec. (1) - (2).
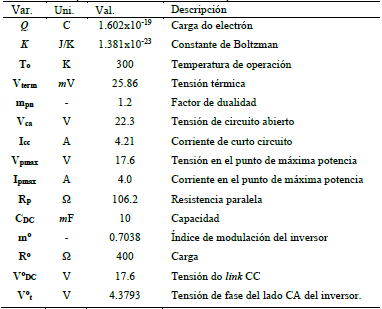
Todos los parámetros utilizados en las ecuaciones anteriores se describen en la tabla 3.
2.2. Curvas características de voltaje, corriente y potencia
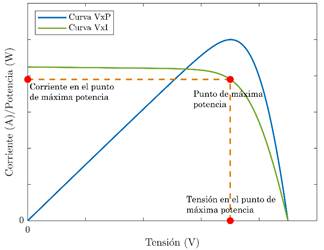
Para que la ecuación (1) sea igual a la ecuación (2), es necesario que las resistencias Rsh y Rs sean infinitas y cero, respectivamente. Valores bajos de Rsh causan una reducción en la corriente debido a la relación entre voltaje y corriente (pérdidas en las células), por el hecho de que parte de la corriente fotogenerada, fluye internamente por el generador fotovoltaico. Valores elevados de Rs aumentan la caída de tensión interna del generador, limitando la corriente fotogenerada y consecuentemente la potencia máxima generada. La Fig. 2 representa la curva característica de corriente, tensión y potencia de un sistema fotovoltaico.
Fuente: Los Autores.
Figura 2 Curva característica de voltaje, corriente y potencia de un panel fotovoltaico.
2.3. Dinámica del sistema fotovoltaico
El modelo dinámico del sistema fotovoltaico se dará por la constitución de un flujo de CC, a través del cual el panel fotovoltaico va a ser cargado, este a su vez será interconectado a un inversor de tensión y así alimentará una carga local. La Fig. 3 representa un diagrama genérico de un sistema fotovoltaico autónomo.
Observando la Fig. 3, se puede obtener la siguiente ecuación para representar la dinámica de un sistema fotovoltaico autónomo.
Considerando que Rs << Rsh (Resistencia en serie mucho menor que la resistencia en paralelo), Se puede escribir la siguiente relación.
Para la representación en espacio de estados, es necesario adoptar las variables de entrada, de estado y de salida a fin de obtener la función de transferencia del sistema linealizado en un punto de operación, considerando lo siguiente:
Variable de entrada - Índice de modulación del variador
Variable de salida - Voltaje de salida de CA del variador
Variable de estado - Voltaje de entrada CC del variador
De esta forma, se verifican las siguientes relaciones.
Para un estudio sobre pequeñas variaciones de las señales, en torno a un punto de operación se realizará la linealización del sistema a través de la serie de Taylor, de esta forma, se obtiene el siguiente sistema linealizado.
A partir de la representación en espacio de estado, se define la siguiente función de transferencia.
Organizando la Ec. (15) se obtiene:
Al definir la función de transferencia del sistema linealizado, es posible proyectar un controlador para un determinado punto de operación del sistema fotovoltaico autónomo.
3. Diseño del controlador PI-Fuzzy
Para el estudio que va a ser implementado en este artículo, se hará una breve introducción de la metodología de control Fuzzy que será utilizada para la realización del control de la tensión CC del Generador Fotovoltaico (GF). En este sentido el sistema Fuzzy está formado por 4 componentes: un procesador ubicado en la entrada que realiza la fuzzificación de los datos de entrada, una base de reglas, una máquina de inferencia para la toma de decisiones y un procesador que proporciona un vector de salida (Wang,1996)(Fernandez,2014).
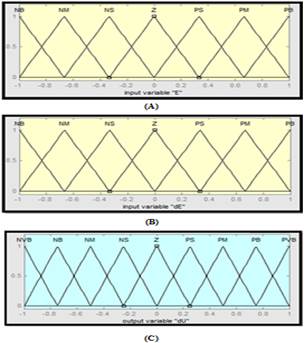
El controlador PI-Fuzzy tiene dos entradas: el error y la derivada del error (variación instantánea del error), y en la salida la derivada de la señal de control (dU) (Wang,1996). En resumen, el controlador PI-Fuzzy hace una búsqueda del valor ideal de la señal de control (U) para ser aplicada en la planta, teniendo como parámetros de referencia el error y la variación del error del sistema. Para el proyecto del controlador PI-Fuzzy, se utilizó el método de Mamdani y las funciones de pertinencias utilizadas para el error y la variación del error fueron triangulares, como se muestra en la Fig. 4.
Fuente: Los Autores.
Figura 4 Función de pertinencia de las entradas y salidas del sistema Fuzzy. (A) - Función de pertinencia de la entrada error. (B) - Función de pertinencia de la entrada derivada del error. (C) - Función de pertinencia de la salida derivada de la señal de control.
Las abreviaturas NVB, NB, NM, NS, Z, PS, PM, PB y PVB significan: Negative Very Big, Negative Big, Negative Medium, Negative Small, zero, Positive Small, Positive Medium, Positive Medium, Positive Big y Positive Very Big. y representan las funciones de pertinencia para el grado de negatividad o positividad de las variables error y derivada del error.
De acuerdo con las funciones de pertinencia presentadas anteriormente, se puede observar que las variables de entrada y salida del sistema Fuzzy admite valores correspondientes al intervalo de [-1, 1]. Por lo tanto, es necesario limitar los valores de las variables dE y E además de ampliar el valor de salida dU para que el sistema opere de la forma deseada. La Tabla 1 presenta la base de reglas constituida para la implementación del controlador Fuzzy. La Fig. 5 presenta un diagrama de flujo del proceso de diseño del controlador PI-Fuzzy.
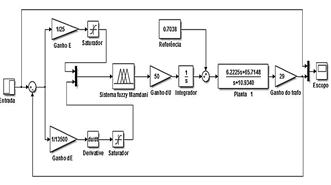
La Fig. 6 muestra el diagrama de bloques del sistema fotovoltaico modelado con el controlador PI-Fuzzy.
4. Metodología
En este trabajo, se desarrolló un modelo matemático que describe adecuadamente la dinámica de un panel fotovoltaico, a continuación, con el objetivo de alcanzar un desempeño deseado, se proyectó un controlador con el fin de realizar la estabilización del bus de CC, así como obtener un rendimiento satisfactorio para el sistema. Inicialmente, se desarrolló un estudio computacional, utilizando el entorno del software MATLAB, para analizar la interacción de las estrategias de control propuestas en el sistema fotovoltaico. A continuación, se desarrollaron las pruebas simuladas y prácticas en un sistema real para verificar las características del panel fotovoltaico, a través de la observación de las curvas de corriente y tensión del sistema, seguidamente, se realizó una evaluación de la dinámica del modelo matemático obtenido, comparando los resultados reales con los resultados simulados. En consecuencia, se desarrolló un sistema embarcado, para implementar los controladores diseñados y aplicarlos en el sistema real. Para la realización de la parte práctica de este estudio, se utilizó el siguiente panel fotovoltaico con la instrumentación desarrollada, como muestra la Fig. 7. La Tabla 2 presenta las especificaciones técnicas del panel utilizado para la realización del estudio. Para el desarrollo del modelo matemático, así como para el desarrollo de la simulación, se utilizó el punto operacional presentado por los parámetros de la Tabla 3.

Fuente: Los Autores.
Figura 7 Sistema fotovoltaico. (A) Panel fotovoltaico Atersa. (B) Banco de lámparas para emulación de la irradiación. (C) Sistema embarcado desarrollado.
Si se utiliza el valor de los parámetros contenidos en la Tabla 3, se puede obtener la siguiente función de transferencia que representa la dinámica del sistema fotovoltaico, como muestra la ecuación 17.
5. Análisis de resultados
5.1. Evaluación experimental del sistema fotovoltaico operando en lazo abierto
Para la realización de la evaluación experimental del comportamiento dinámico del sistema fotovoltaico, se hace necesario la observación del comportamiento de las curvas de tensión y corriente conjuntamente con la asociación de dos módulos fotovoltaicos, inicialmente se observa su comportamiento con estos paneles conectados en serie y en paralelo, con carga de alimentación de una batería de 12V y los módulos se encuentran en la asociación serie, de esta forma el gráfico se inicia con un valor de tensión cercano a 42 V, ver Fig. 8. Teóricamente, el valor de tensión de esta asociación debería ser de 44,6 V, esta diferencia se debe al hecho de que la temperatura de operación del módulo es diferente al del estándar (25°C), pues en el momento de la realización del experimento los sensores térmicos indicaban el valor de 39,8°C, siendo este valor medido en el centro de la parte posterior de cada panel. En el momento en que la llave selectora ajusta la tensión de salida para la batería, la tensión cae y comienza a fluir una corriente de carga por la misma, después de unos segundos, se cambia la asociación de serie a paralelo, doblando el valor de la corriente. Se puede verificar tales situaciones a través de la Fig. 8, donde se observa que la curva de color blanco representa el nivel de tensión y la curva de color rojo representa el nivel de corriente.

Fuente: Los Autores.
Figura 8 Curvas de tensión y corriente según la asociación de los paneles fotovoltaicos.
Se puede observar que hay cuatro transiciones, que se produjeron por las siguientes razones:
5.2. Validación del modelo matemático desarrollado
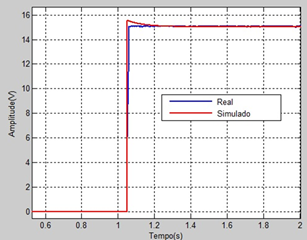
Con el fin de validar el modelo desarrollado, se realizó la prueba de lazo abierto en el sistema real, comparándolo con el comportamiento del sistema simulado. La Fig. 9 presenta el comportamiento de la planta real y del modelo simulado.
Se puede verificar en la Fig. 9, que el modelo desarrollado representa adecuadamente el sistema en cuestión, validando de esta manera el modelo matemático obtenido.
5.3. Evaluación en ambiente computacional del sistema fotovoltaico operando en lazo cerrado con los controladores implementados
Para la aplicación del control de tensión del bus CC, se desarrolló un controlador discreto a través del método indirecto de proyecto de controladores, se proyectó el controlador en el dominio continuo de la frecuencia y luego se transportó el resultado para el dominio de tiempo discreto haciendo uso del método de Tustin, para el diseño del controlador clásico por la técnica de asignación de polos. A continuación, se utilizó el método de Tustin para la obtención del equivalente discreto del sistema, con el tiempo de muestreo de 0.01 segundos, obteniéndose la relación (18). La Tabla 4 representa las especificaciones de rendimiento utilizadas para el proceso de obtención del controlador clásico.
Fuente: Los Autores.
Figura 9 Validación del modelo fotovoltaico desarrollado, comparando ambos modelos tanto el sistema real como el simulado.
Tabla 4 Especificación de rendimiento deseada para el sistema en lazo cerrado malla cerrada.

Fuente: Los Autores.
A continuación, se comparó el controlador clásico con el controlador Fuzzy de baja ganancia. La Fig. 10 representa la respuesta en lazo cerrado de un sistema fotovoltaico, haciendo uso de las dos estrategias de control arriba citadas. En la Fig. 10, se observa que el sistema se inicia en 2 segundos, presentando una tensión de referencia de 127 V, a los 6 segundos se produce un cambio del setpoint a 60 V.

Fuente: Los Autores.
Figura 10 Análisis en ambiente computacional de la variación del setpoint de tensión.
Se observa en la Fig. 10, que el controlador PI-Fuzzy con bajo valor de ganancia, tiene un pequeño retardo para la realización del control durante el arranque, sin embargo, este presenta un valor reducido del máximo sobrepaso y un tiempo de asentamiento menor, cuando comparado con el controlador PI proyectado por la técnica de asignación de polos.
Con el fin de mejorar la respuesta transitoria del sistema con el controlador Fuzzy, se ha incrementado la ganancia estática en una proporción de 10 veces. La Fig. 11 presenta la respuesta del sistema fotovoltaico, haciendo uso de las dos estrategias de control abordadas en este estudio, la estrategia de control Fuzzy y clásica tuvieron sus aumentos estáticos amplificados en una proporción de 10 veces.

Fuente: Los Autores.
Figura 11 Análisis en ambiente computacional de la variación del (setpoint) punto de consigna de tensión.
Se observa en la Fig. 11 que el aumento de la ganancia estática proporcionó una sensible mejora en la respuesta transitoria del sistema, de modo que el controlador mediante la asignación de polos tornó el sistema menos oscilatorio y disminuyó el tiempo de asentamiento, también se observa que dicho aumento de la ganancia en el controlador Fuzzy proporcionó una mejora en la respuesta transitoria y disminuyó el tiempo de retraso durante la partida del sistema. Se verificó una mejora también a través de la disminución del tiempo de asentamiento del sistema.
5.4. Evaluación experimental del sistema fotovoltaico operando en lazo cerrado con los controladores proyectados
Después de un breve análisis y evaluación del comportamiento del sistema en ambiente computacional, se realizó un análisis experimental con relación a la comparación de los resultados presentados por las respectivas técnicas de control.
La Fig. 12 representa la respuesta en lazo cerrado de un sistema fotovoltaico real, utilizando las dos estrategias de control arriba citadas. En esta figura se observa que en el momento de partida del sistema hay un aumento en la tensión, por parte del controlador clásico, mientras que el controlador Fuzzy presenta un menor tiempo de asentamiento inferior al del controlador clásico, ratificando los resultados obtenidos en las simulaciones realizadas con el modelo desarrollado. A continuación, se realizó una variación del punto de consigna (setpoint) del valor de referencia de la tensión, con el objetivo de observar el comportamiento dinámico de los controladores. De este modo se observa que el controlador Fuzzy presentó un mejor desempeño con relación al controlador clásico, presentando bajo sobrepaso, así como menor tiempo de asentamiento, corroborando los resultados obtenidos a través del entorno computacional.
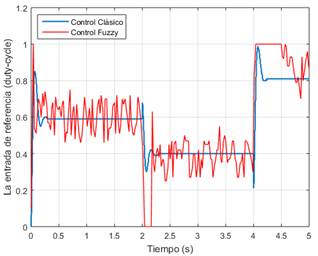
La Fig. 13 representa la señal de control del convertidor de potencia conectado al bus CC, mostrando el ciclo de trabajo de la llave estática.
Fuente: Los Autores.
Figura 13 Evaluación experimental de la señal de control de las técnicas de control abordadas, caracterizando el ciclo de trabajo de la llave estática del convertidor de potencia del bus CC.
Se observa en la Fig. 13, una mayor variación de la señal de control por parte de la metodología Fuzzy en comparación a la clásica, así como una mayor demanda energética. Tal hecho se justifica con el fin de suavizar las oscilaciones de la tensión de salida y garantizar el desempeño deseado a través del controlador implementado.
La Fig. 14 representa la evaluación experimental del error relativo, dado en porciento relacionado a la salida del sistema fotovoltaico. Se observa en la Fig. 14 que el error relativo relacionado al sistema en lazo cerrado con la aplicación del controlador Fuzzy presenta menor amplitud, ratificando el buen desempeño de la técnica de control Fuzzy en comparación a la técnica clásica de control.

Fuente: Los Autores.
Figura 14 Evaluación experimental del error relativo porcentual de la salida del sistema fotovoltaico.
La Tabla 5 presenta un análisis comparativo entre la aplicación de las dos técnicas de control propuestas (Control Fuzzy versus Control Clásico (técnica de asignación de polos), para observar la evaluación de algunos parámetros de desempeño, siendo estos: tiempo de asentamiento, máximo sobrepaso y la función de costo ISE (Integral Square Error).
Tabla 5 Análisis comparativo de los parámetros de desempeño de las metodologías de control empleadas.

Fuente: Los Autores.
En la Tabla 5 se muestran los valores de rendimiento del sistema con ambas estrategias de control aplicadas en este trabajo, así como sus respectivas evaluaciones en ambiente de simulación y experimental, se verificó que el controlador Fuzzy para ambas pruebas tanto experimental como computacional presentó mejores índices de desempeño y de rendimiento, corroborándose de este modo su utilización para aplicaciones en sistemas fotovoltaicos.
6. Conclusiones
Este trabajo presentó una propuesta del modelado de un sistema fotovoltaico autónomo, así como la validación del modelo dinámico propuesto y la realización de una evaluación experimental de las estrategias de control PI clásico (método de asignación de polos) y PI-Fuzzy aplicadas a un sistema fotovoltaico real, con el objetivo de realizar un control de tensión del bus CC y realizar una variación de la tensión de referencia en la salida del sistema. Se realizó un análisis comparativo, a través de pruebas experimentales en un sistema real fotovoltaico con las técnicas de control clásico y control Fuzzy. Los resultados obtenidos demostraron un rendimiento superior del controlador Fuzzy con relación al controlador clásico, en cuanto a la evaluación del comportamiento dinámico del sistema fotovoltaico, en el que el controlador Fuzzy presentó un tiempo de asentamiento inferior al del controlador clásico, así como la reducción de la tensión, cuando se sometió el sistema a la prueba de variación de la tensión de referencia. De este modo, los resultados confirman un mejor rendimiento del controlador Fuzzy para su aplicación en un sistema fotovoltaico autónomo.