INTRODUCTION
Gatifloxacin (1-cyclopropyl-6-fluoro-8-methoxy-7-(3-methylpiperazin-1-yl)-4-oxoquin-oline-3-carboxylic acid; CAS: 112811-59-3) (figure 1) is an antibiotic agent and a member of the fourth-generation fluoroquinolone family. It works by inhibiting the bacterial enzymes DNA gyrase and topoisomerase IV [1,2]. Gatifloxacin is effective against a broad spectrum of bacteria that may cause ocular infections in humans including endopthalmitis and conjunctivitis. Melo et al. found that gatifloxacin was effective against a range of both Gram positive and Gram negative microorganisms including anaerobes when tested in vitro, which transforms this drug into a dangerous agent for the aquatic systems, if used indiscriminately [3].
In addition, the pharmaceutical industry is a potential source of contamination, since most processes, such as synthesis, purification of raw materials, chemical analysis for quality assessment, and pre-formulation and formulation studies, tend to produce large masses of waste containing these chemical agents [4, 5].
In this sense, the development of strategies that lead to the design of more environmental-friendly methodologies, focused on environmental management systems supported by ISO 14001, and leading to promoting the development of cleaner production practices have been consolidated as an important tool for the prevention and correction of contaminating processes [6, 7]. Thus, the generation of experimental data and the development of mathematical models that allow predicting properties such as solubility contribute greatly to reducing experimental tests, which in turn decreases the mass of pollutants (e.g., drugs, solvents, disposable material, and energy) produced in processes of the pharmaceutical industry [8, 9].
In this context, mathematical models tending to predict the solubility of drugs in different solvents and/or cosolvents mixtures at different temperatures have become an important tool for the pharmaceutical industry [10], not only for drugs but also for other large organic molecules, such as polycyclic aromatic hydrocarbons, which, like drugs, are also a source of contamination by the oil industry [11, 12]. Thus, based on thermodynamic properties, models such as the "nearly ideal binary solvent" approach by Acree et al. allow to successfully determine solubility in some types of cosolvent mixtures [13, 14]. Another model, which is an improvement of the previous one, is that proposed by Jouyban et al., which involves polar and non-polar solvents [15, 16]. Other models based on area surfaces, contribution of UNIFAC groups, Hildebrand solubility parameters, and Kirkwood-Buff integrals have been proposed and refined to improve their predictability [17-20].
Thus, based on the solubility data of gatifloxacin in AA-Dimethylformamide + methanol cosolvent mixtures, published by Wu et al. [21], and some data on the physicochemical properties of the drug (table 1) [22], the objective of the present work is perform a thermodynamic analysis and of preferential solvation.
Table 1 Physicochemical information of the gatifloxacin.
| Chemicals | CAS reg. no. | molar mass / g mol-1 | Melting point / K | Melting enthalpy / kJ mol-1 |
| Gatifloxacin | 112811-59-3 | 375.39 | 435.15a | 34.95a |
a Ref [22].
RESULTS AND DISCUSSION
Solubility of Gatifloxacin in DMF + methanol cosolvent mixtures
Figure 2 show the solubility of gatifloxacin (3) in DMF (1) + methanol (2) cosolvent mixtures, in this plot, can look an increase in solubility, as a consequence of an increase in temperature, which implies that the solution process in DMF (1) + methanol (2) cosolvent mixtures is favored by supplying energy to the system. This demonstrates that the process is endothermic [23, 24], where we can obtain the lowest solubility in pure methanol at 273.15 K (1.9 x 10-4) and the maximum solubility in pure DMF (9.891 x 10-3) at 318.15 K.
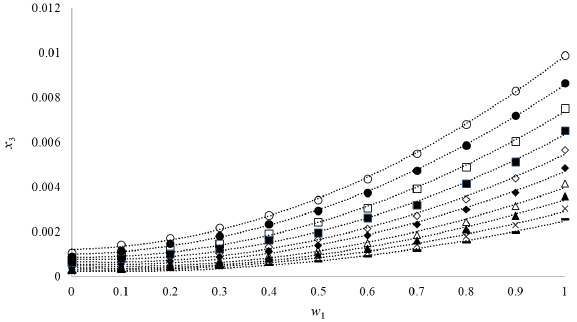
Figure 2 Solubility of gatifloxacin (3) expressed in molar fraction (x3) in DMF (1) + methanol (2) cosolvent mixtures as a function of mass fraction at different temperatures. -: 273.15, x: 278.15 K; ▲ : 283.15 K; A: 288.15 K; ♦: 293.15 K; ◊: 298.15 K; ■ 303.15 K; □: 308.15 K; •: 313.15 K; and o: 318.15 K.
According to Hildebrand's theory, it would be expected that the maximum solubility would be reached in a cosolvent mixture and not in a pure solvent, as it happens in this case, because the polarity of la gatifloxacin (28.08 MPa1/2 [25, 26]) (table 2) is between the polarity of DMF (24.1 MPa1/2 [25]) and the polarity of methanol (29.7 MPa1/2) [25].
Activity coefficients
From the activity coefficients, the possible molecular interactions that govern the process of gatifloxacin solubility in the DMF + methanol cosolvent mixture can be inferior.
Table 3 presents the values of the activity coefficients in the DMF + methanol cosolvent system at nine temperatures calculated according to equation 1 [27], from the solubility data [21] and the ideal solubility calculated according to equation 2, which can be analyzed based on the solute-solute (e33), solvent-solvent (e11), and solute-solvent (e13) molecular interactions using equation 3 [28]:
Table 3 Coefficient activity of gatifloxacin (3) in DMF (1) + methanol (2) cosolvent mixtures at different temperatures and pressure p = 0.1 MPa.
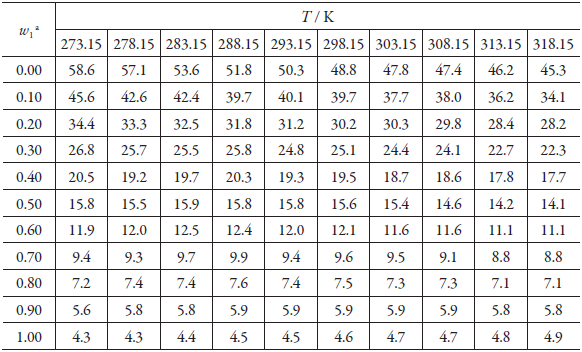
a W 1 , mass fraction of DMF (1) in the gatifloxacin -free DMF (1) + methanol (2) mixture.
here x3 id is the ideal solubility of the solute as mole fraction, Δ fus H is the molar enthalpy of fusion of the pure solute (at the melting point), T fus is the absolute melting point, T is the absolute solution temperature, R is the gas constant (8.314 J mol-1 K-1), and ΔC p is the difference between the molar heat capacity of the crystalline form and the molar heat capacity of the hypothetical super-cooled liquid form, both at the solution temperature. Since ΔC p cannot be easy experimentally determined it is usual assuming that it may be approximated to the entropy of fusion, Δ fus S [29,30].
where V 3 is the molar volume of the supercooled liquid solute, and finally, ф 1 is the volumetric fraction of the solvent. A good approximation, for relatively low solubilities, is that the term V 3 φ 2 1 /RT can be considered a constant, and therefore, ln γ3 depends solely on e 11 + e 33 - 2e13 [31]. The e11 and e 33 terms are unfavorable for drug solubility and the term e13 favors the solubility thereof[32].
In all cases (table 3), the activity coefficients are greater than unity, which according to equation 3 [33], indicates that the solute-solute (e 33) and solvent-solvent (e 11) molecular interactions, which demerit the process of the solution, surpass the solute-solvent interactions, which favor the process.
In general, with an increase in temperature, the activity coefficients decrease and the cosolvent system's polarity decreases; thus, from pure methanol to the pure DMF, the activity coefficients decrease, showing a possible increase in the solute-solvent interactions, due to increased solubility of gatifloxacin (e 13 ).
Thermodynamic functions of solution
The standard thermodynamic functions of the solution (table 4) are calculated from the experimental solubility data and study temperatures. Thus, the mathematical expressions of Gibbs and van't Hoff, under Krug's approach, are presented as follows [4, 34, 35]:
where Thm is the harmonic temperature, Δ soln G° is the standard Gibbs energy of solution, AsolnH° is the standard enthalpy of solution, and Δ soln S° is the standard entropy of solution. ξ H yξ TS <; TS are the enthalpy and entropy contributions to the solution process and the intercept corresponds to the linear equation of the plot ln x 3 vs. (1/T - 1/T hm) [36, 37].
Table 4 Thermodynamic functions of solution of gatifloxacin (3) in DMF (1) + methanol (2) cosolvent mixtures at 294.95 K and pressure p = 0.1 MPa.
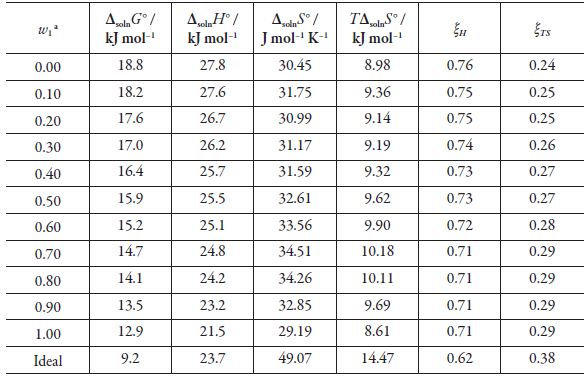
aW1 is mass fraction of DMF (1) in the gatifloxacin-free DMF (1) + methanol (2) mixture.
Gibbs energy is positive in all cases and decreases from pure methanol to pure DMF. As for the standard solution, it is positive in all cases, indicating an endothermic process, and decrease from pure methanol to pure DMF, possibly due to an increase in solute-solvent interactions, which is consistent with the gatifloxacin solubility increase in DMF-rich mixtures and pure DMF.
Regarding the standard solution entropy, it is positive in all cases, presenting an entropic favor to the gatifloxacin solution process in DMF + MeOH cosolvent mixtures.
From the results of equations 8 and 9, it can be concluded that the solution process is favored in all cases by enthalpy. A graphical method that allows corroborating the previously exposed is that developed by Perlovich (figure 3) (all values are within sector I: Δsoln H° > TΔsoln S° > 0 [38, 39]). Thus, the contribution of the solution's standard enthalpy to Gibbs energy values in all cases is greater than 71%, being greater in methanol-rich mixtures and less in DMF-rich mixtures.
Although there is an enthalpy predominance, the solution entropy promotes a decrease in Gibbs energy values, which generally favors the solution process.
Thermodynamic transfer functions
One way to identify the cosolvent effect on the thermodynamic behavior of the solution process is to analyze the transfer functions. Starting from a hypothetical transfer process from a medium of greater polarity to a medium of lower polarity, the thermodynamic transfer functions are calculated as [40]:
where, f represents thermodynamic functions, Gibbs energy, enthalpy, or entropy.
Table 5 shows the most representative values of the gatifloxacin transfer process from pure methanol to pure DMF. From the results of equation 10, a Perlovich plot [39] (figure 4) is drawn, which provides a good analysis of the results.
Table 5 Thermodynamic functions of transfer of gatifloxacin (3) in DMF (1) + methanol (2) co-solvent mixtures at 294.95 K and pressure p = 0.1 MPa.
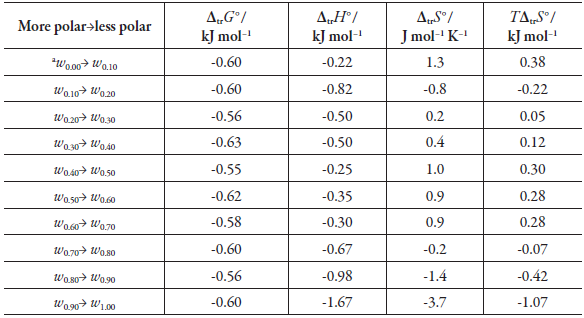
1 wj, mass fraction of DMF (1) in the gatifloxacin-free DMF (1) + methanol (2) mixture. 2.0
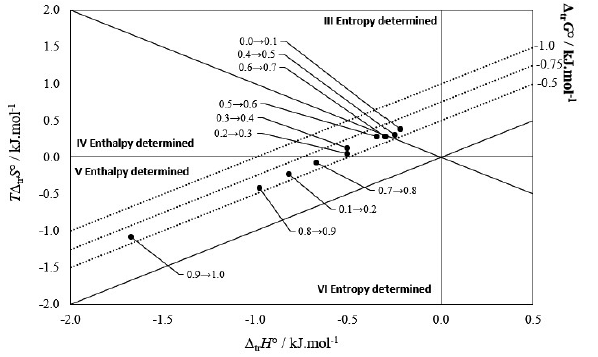
Figure 4 Relationship between the enthalpy (Δtr H°) and entropy (TΔtr S°) terms of the transfer process of gatifloxacin from more polar mixtures to less polar mixtures at 294.95 K. The isoenergetic curves of Δtr G° are represented by dotted lines.
Thus, according to the Perlovich plot [4, 37, 39, 41, 42], from pure methanol to W0J0 (Sector III Δtr H° < 0, TΔtr S° > 0, and |TΔtr S°| > |Δtr H°|) the process is driven by entropy; from w010 to w020 (Sector V Δtr H° < 0, TΔtr S° < 0, and |TΔtr S°| < |Δtr H°|) the process is driven by enthalpy; from w 020 to w 040 (Sector IV Δtr H° < 0, TΔtr S° > 0, and | TΔtr S°| < |Δtr H o |), the process is again driven by enthalpy; from w 0.40 to w 0.50 (Sector III Δtr H° < 0, TΔtr S 0 > 0, and |TΔtr S ° | > |Δtr H o|) the process is driven by entropy; from w0.50 to w0.70 (Sector IV Δtr H° < 0, TΔtr S° > 0, and |TΔtr S°| < |Δtr H >|), the process is driven by enthalpy and from w 0.70 to pure DMF (Sector V Δtr H° < 0, TΔ tr S° < 0, and | TΔ tr S o | < |Δtr H°|) the process continues to be driven by enthalpy.
So, in all cases there is an enthalpy favor (negative enthalpy), therefore there is an enthalpy conduction in the whole process, however, from w a10 to w020 and from w 090 to DMF the entropy is negative, therefore, entropy disadvantages the transfer process. In other cases, entropy is positive, indicating that the solution process is favored by enthalpy and entropy.
Thermodynamic functions of the mixing
The solute behavior in the dissolution process can generally be divided into two stages, the solute fusion and its subsequent mixing with the solvent, so this hypothetical process can be represented according to the following scheme [43, 44]:
In this way, thermodynamic solution functions can be represented by the following equation:
where, f represents the thermodynamic functions (G, H or S) and the subscripts f and mix represent fusion and mixing, respectively.
Thus, the mixing functions are determined as [45]:
where Δf f 0 is replaced by the ideal thermodynamic functions, which are thus calculated as[46]
Table 6 shows the thermodynamic mixing functions; from pure methanol to pure DMF, the mixing Gibbs energy decreases in value as the DMF concentration increases, whereby the DMF addition has a positive cosolvent effect, favoring the solvent-solvent interactions (e13). As for the mixing enthalpy, it is positive from pure methanol to w 1 = 0.8, this factor it does not favor the dissolution process, it is observed that the enthalpy is greater in methanol-rich and intermediate mixtures possibly due to the fact that the formation of the cavity (required for solute accommodation) in these mixtures requires more energy. The foregoing may indicate that MeOH-MeOH interactions are stronger than those of DMF-DMF, In DMF-rich mixtures (0.90 ≤ w 1 ≤ 1.00), the enthalpy is negative, which favors the mixing process.
Table 6 Thermodynamic functions of mixing gatifloxacin (3) in DMF (1) + methanol (2) cosolvent mixtures at 294.95 K and pressure p = 0.1 MPa.
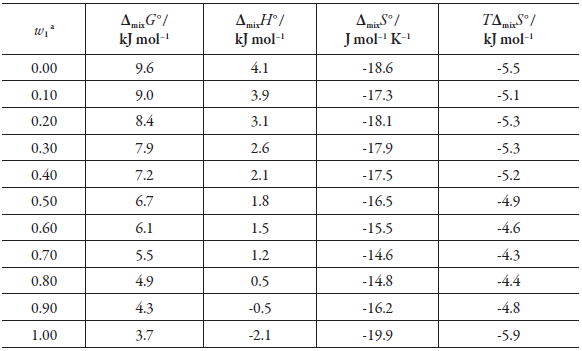
a W1, mass fraction of DMF (1) in the gatifloxacin -free DMF (1) + methanol (2) mixture.
Regarding the entropy of the mixture, it is negative in all cases, which unfavors the mixing process.
From Perlovich's analysis (figure 5), it is concluded that in all cases the process is driven by entropy, both in the sector VII, from pure methanol to w 1 = 0.80 (sector VII: Δmix H° < TΔmix S° and |TΔmixS°| > |Δmix H 0|), and in the sector VI, from W 1 = 0.90 to pure DMF (sector VI: Δmix H°< 0, TΔmixS° < 0, and |TΔmixS°| > Δmix H°|).
Enthalpy-entropy compensation
An analysis that identifies changes in the mechanism that controls the cosolvent action is that of enthalpy-entropy compensation, which is performed by plotting Δsoln H° vs. Δsoln G°, where in most cases, a nonlinear behavior is observed. Thus, this graphic analysis allows to identify the thermodynamic consequences of bond formation and rupture, where the hydrogen bond is the most relevant interaction [42, 47].
The plot interpretation (Δsoln H° vs. Δsoln G°) is based on the sign of the slopes; thus, negative slopes indicate that the process is entropy-driven, which may be a consequence of the system's molecular rearrangement, while positive slopes indicate that the process is enthalpy-driven, which could be a consequence of changes in intermolecular interactions between the drug and solvents through hydrogen bonds and van der Waals forces such as the induced or permanent dipole-dipole interactions, and therefore, can be considered as quantitative indicator of changes in the intermolecular bond energies that occur during the interaction [48-50].
Figure 6 shows the behavior of gatifloxacin enthalpy-entropy compensation in the DMF + MeOH system. Thus, in all cases the solution process is driven by enthalpy.
Preferential solvation
An analysis that allows a more precise evaluation of molecular interactions and solvent composition in the immediate environment of solute molecules, is the mathematical model proposed by Ben-Naim denominating the inverse Kirkwood-Buff integral (IKBI) [51-53], which expresses its results according to the preferential solvation parameters δx 1,3 and δx23, indicates the solute preference (3) for solvent (1) or (2) according to [10, 54, 55]:
where x 1 is the mole fraction of 1 in the cosolvent mixture and x L 1,3 , is the local mole fraction of 1 in the vicinity of the solute (3). If δx13 > 0, the solute is preferentially solvated by 1, and if <δx13 < 0, the solute is preferentially solvated by 2. However, if |<δx13| ≤ 0.01, the values are probably within the error of determination, indicating an insignificant preferential solvation. On the other hand, if <δx1,3 ≈x2, it means that x L 13 = 1 or a complete preferential solvation of 3 by 1 [10, 54].
The application expressions of the IKBI approach given by Ben-Naim are [56, 57]:
where G 1,3 and G 2,3 are the Kirkwood-Buff integrals (in cm3 mol-1) and V cor is the volume of correlation around 3 (gatifloxacin), within which preferential solvation occurs. Thus, G 1,3 and G 2,3 are calculated as [58, 59]:
and the correlation volume is calculated as [54, 60 ,61]:
where K T is the isothermal compressibility of DMF + MeOH mixtures (DMF: 0.698 GPa-1 [62], Methanol: 1.248 GPa-1 [63]), V 1 and V 2 are DMF and methanol Gadžurić et al. [64] and Kijevčanin et al. [65], V3 is the molar volume of gatifloxacin (232 cm3 mol-1), r is the radius of the gatifloxacin molecule (0.4476 nm), and D and Q (in kJ mol-1, as RT) are calculated using equations 21 and 22 [66, 67]:
Δt G°3,2→1+2 is the transfer Gibbs energy of gatifloxacin from the methanol to each DMF + MeOH cosolvent mixture (equation 23), and G E 1,2 is the excess Gibbs energy of the cosolvent mixture of DMF + MeOH free of gatifloxacin (equation 24) [54, 68]:
The values of D, G 1,3 G 2,3, V cor and δx 1,3 are presented in table 7, and the behavior of δx 1,3 is presented in Figure 7. The δx 1,3 values show that the preferential solvation of gatifloxacin by both methanol (from pure methanol to w 1 = 0.25, δx1,3 has negative values) and DMF (From w 1 = 0.25 to pure DMF, δx 1,3 has positive values) is insignificant, because all the δx1,3 values are less than 0.01.
Table 7 Solubility and preferential solvation of gatifloxacin in DMF+ methanol mixtures at 313.15 K.
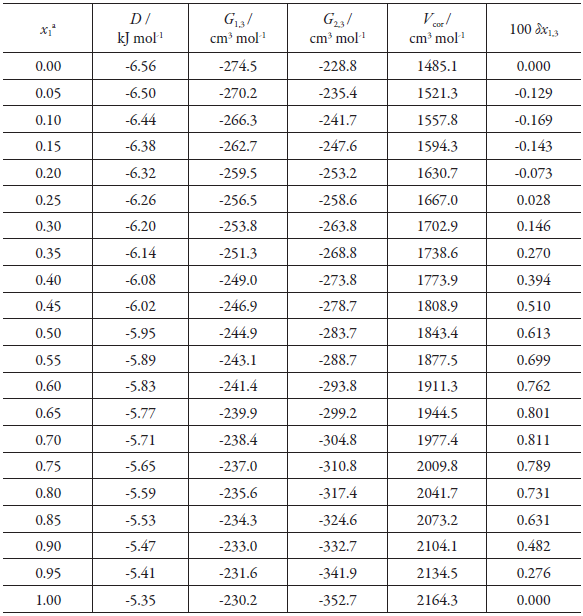
a X 1 , mole fraction of acetonitrile (1) in the gatifloxacin-free DMF (1) + methanol (2) mixture.
It could be expected (however, because the values of <δx1,3 are less than 0.01, the analyzes are not conclusive) that the gatifloxacin, it behaves as a Lewis base against the methanol-rich medium because the methanol (β = 0.62 [69]) has a less basic character than DMF (β = 0.71 [70]) according to the β -scale of Taft and Kamlet, and like a Lewis acid against the DMF. Table 7. Some properties associated to preferential solvation gatifloxacin (3) in DMF (1) + MeOH (2) cosolvent mixtures at 313.15 K and pressure p = 0.096 MPa.
CONCLUSIONS
From thermodynamic analysis and preferential solvation of gatifloxacin in DMF + MeOH cosolvent mixtures, it is concluded that the solution process is endothermic with a marked enthalpy favor, which increases as the polarity of the cosolvent system decreases due to the addition of DMF, presenting a positive cosolvent effect that leads to increased gatifloxacin solubility. Finally, regarding gatifloxacin's preferential solva-tion, the results are not conclusive, because in all cases the values of the preferential solvation parameter are less than 0.01, so that, negligible preferential solvation takes place.



































