Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Entomología
Print version ISSN 0120-0488On-line version ISSN 2665-4385
Rev. Colomb. Entomol. vol.35 no.1 Bogotá Jan./June 2009
Sección Médica
Simulando manejo de Aedes aegypti (Diptera: Culicidae) y sus efectos en una epidemia de dengue
Simulating management of Aedes aegypti (Diptera: Culicidae) and its effects in a dengue epidemic
JONNY EDWARD DUQUE L.1,2, MARIO ANTÔNIO NAVARRO-SILVA1 y DECCY YANETH TREJOS A.3
1 Laboratório de Entomologia Médica e Veterinária, Departamento de Zoologia, Universidade Federal do Paraná. Curitiba - Brasil. Caixa Postal 19020, 81531-980 Curitiba, PR. Telefone: (41) 3361-1640. Fax: (41) 3361-1763. jonnybiomat@ufpr.br; jonnybiomat@hotmail.com. Autor para correspondencia.
2 Programa de becas Prodoc/Capes (Programa de Apoio a Projetos Institucionais com a Participação de Recém-Doutores /Coordenação de Aperfeiçoamento de Pessoal de Nível Superior) do Ministerio da Educaçao, Brasilia D. F., Brasil.
3 Grupo de investigación en Ciencia Matemática y Tecnología. Proyecto Curricular Matemáticas, Universidad Distrital Francisco José de Caldas. Bogotá D. C., Colombia.
Resumen: Se simuló un modelo matemático tipo SEIR (Susceptible, Expuesto, Infeccioso y Removido) que incluye una población de hospederos humanos, vectores del dengue y estrategias de control de Aedes aegypti. Las simulaciones indicaron que las aplicaciones de los insecticidas deben ser combinadas en los estados larvarios y adultos del vector para disminuir rápidamente la epidemia. También, se observó que para no comprometer el control del mosquito, es necesario que los insecticidas sean altamente efectivos, que las aplicaciones tengan alta cobertura de efectividad, y que estén siempre acompañados de remoción constante de criaderos. Se concluye que las densidades del vector deben ser mantenidas próximas a cero en todos los períodos del año para evitar al máximo la coexistencia hospedero - vector.
Palabras clave: SEIR. Resistencia química. Control de mosquitos.
Abstract: A SDIR (Susceptible, Displayed, Infectious and Removed)-type mathematical model was simulated which included a population of human hosts, dengue vectors, and control strategies for Aedes aegypti. The simulations indicated that applications of insecticides should be combined in both the larval and adult stages of the vector in order to quickly reduce the epidemic. In order to avoid compromising control of the mosquito, it is also necessary to use highly efficient insecticides, ensure that applications have highly effective coverage, and that they are always accompanied by constant removal of breeding sites. It is concluded that densities of the vector must be kept close to zero throughout the year to avoid the coexistence of virus and vector.
Key words: SEIR. Chemical resistance. Mosquito control.
Introducción
La dispersión a varios lugares y el aumento de casos de dengue y sus manifestaciones clínicas más graves en las últimas décadas ha sido responsabilizado hasta ahora a factores como la urbanización no planeada, cambios demográficos y la posibilidad que tienen los humanos de migrar en gran escala para cualquier lugar del mundo como consecuencia de las facilidades de transporte aéreo y terrestre (Kroeger y Nathan 2006). A pesar de existir suficiente conocimiento relacionado con esta enfermedad desde hace dos siglos, continua siendo uno de los principales problemas de salud pública que necesita ser solucionado urgentemente (Periago y Guzmán 2007). Dentro de las estrategias de control del dengue, está la reducción de la densidad poblacional del vector Aedes aegypti (Linnaeus, 1762) por medio de la aplicación de productos químicos y biológicos y la eliminación física de criaderos potenciales de las formas inmaduras del vector.
Para existir un brote de dengue, es necesario el contacto entre el vector y una persona portadora del virus en la fase transmisible. Otra posibilidad es que se origine mediante la transmisión vertical, esto es cuando el virus es transferido a las generaciones siguientes del vector sin que haya un contacto con una persona infectada. Según Joshi et al. (2002), esta última forma solo se da en tasas reducidas de transmisión como se ha demostrado en individuos de A. aegypti y su significado para mantener la epidemia es desconocido. Por tanto, es necesario evitar la coexistencia de vectores y personas infectadas, o por lo menos entender hasta qué punto éste puede darse sin el riesgo de brote epidémico.
Entidades de salud de los países donde hay programas de prevención de esta enfermedad hacen esfuerzos significativos para controlar el vector, desafortunadamente, con efectos apenas temporales en la disminución de los casos. El resultado de estos programas se refleja en epidemias con un elevado número de casos después de un periodo de baja incidencia (Duque 2008). Un diseño experimental que explique este fenómeno en gran escala es prácticamente imposible debido a la falta de control de las muchas variables ligadas epidemiológicamente a esta enfermedad, como por ejemplo la cantidad de vectores y personas infectadas necesarias para iniciar un epidemia, el papel de la inmunidad a un serotipo específico del virus, la inmunidad colectiva relacionada con los brotes de la enfermedad, el impacto de las estrategias de control basadas en insecticidas químicos y la remoción de criaderos potenciales del vector.
Una forma más apropiada para entender todas estas variables en conjunto y en escala global es a través de modelos matemáticos (Hasting 1997). Trabajos con diferentes enfoques epidemiológicos y abordajes matemáticos han explicado la dinámica de transmisión del dengue clásico con población humana constante y población humana variable (Esteva y Vargas 1999), incluyendo la transmisión vertical en el mosquito (Esteva y Vargas 2000), la dinámica de transmisión de los diferentes serotipos de virus (Esteva y Vargas 2003), la dinámica de la estructura poblacional (Neil et al. 1999; Pongsumpan y Tang 2003) y patrones espaciales (Bartley et al. 2002). También Derouich y Boutayeb (2006) simularon el efecto de una vacuna hipotética junto a programas de disminución del vector, mostrando ésta como la única posibilidad de erradicación de la enfermedad, toda vez que los tratamientos enfocados en la reducción del vector solamente retardan el surgimiento de la epidemia.
Newton y Reiter (1992), cuestionan el control químico del vector en el estado adulto con aplicaciones de insecticidas ultra bajo volumen (UBV), indicando que con esto solo se consigue un impacto mínimo en la incidencia de la enfermedad y que apenas retardan el surgimiento de la epidemia. En el trabajo de Burattini et al. (2008) se incluyen varios aspectos de Newton y Reiter (1992), como la influencia de la estacionalidad en la relación vector-dengue, diferentes estrategias de control del vector en los estados larvales y adultos, y concluyen que es posible cortar rápidamente la prevalencia nuevos casos de dengue aplicando múltiples métodos de ataque al vector.
Nuestra hipótesis es que en un contexto meramente entomológico, el control del vector está enfocado a la disminución parcial del vector, fallando principalmente en el control de adultos. Dentro de esta idea varios factores tienen diferentes pesos en la efectividad de control y que se expresan negativamente en el aumento de los casos año a año. Así, vemos, aspectos que no permiten éxito en el control de A. aegypti como la resistencia a insecticidas y la baja cobertura de las aplicaciones de insecticidas que permiten que las hembras del mosquito no sean alcanzadas por estos tratamientos (Perich et al. 2000; Castro et al. 2007). El éxito de esta tarea está directamente relacionado con la concientización y el compromiso de la sociedad por medio de acciones individuales y colectivas de eliminación de criaderos del vector. Es evidente que el aumento del número de casos de dengue en los últimos años, confirma que estas acciones están fallando. Una de las posibles soluciones sería una vacuna que confiera inmunidad a toda la población y contra todos los serotipos del dengue DEN-1, DEN-2, DEN-3 e DEN-4 (Gubler 1998), desafortunadamente, esta posibilidad está lejos de ser alcanzada a corto plazo.
Con este escenario de probabilidades en el control entomológico, tenemos como objetivo simular un brote epidémico de dengue incluyendo varias estrategias ligadas a posibles problemas que comprometen el control de vectores, como son la resistencia a insecticidas químicos, baja cobertura de las aplicaciones de los insecticidas y actividades preventivas ejercidas por el hombre para control del vector.
Materiales y Métodos
El modelo de transmisión de dengue propuesto aquí es una modificación del trabajo de Newton y Reiter (1992). Este fue seleccionado por incluir la hipótesis de inefectividad de los insecticidas utilizados para controlar el estado adulto del vector en una epidemia. Se realizaron alteraciones en las ecuaciones originales para observar el comportamiento de las variables en un contexto hipotético con diferentes opciones de tratamiento del vector. Se resaltan escenarios para pensar en resistencia química, efectividad de las aplicaciones de insecticida relacionada con la cobertura de criaderos alcanzados y actividades preventivas ejercidas por el hombre para control del vector, como campañas de limpieza para eliminación de criaderos potenciales del vector.
Se siguen los principios de un modelo tipo SEIR –Susceptibles, Expuestos, Infectados y Removidos– o inmunes al virus. Así, se consideran dos poblaciones: los hospederos humanos (susceptibles, expuestos, infectados y removidos) y los vectores (susceptibles, expuestos, infectados). Las variables del modelo son descritas por ecuaciones diferenciales ordinarias de la forma  = FR x X, donde X es la variable de estado, t es el tiempo y FR es una tasa de incremento. Esta, puede ser constante o depender de otras variables del sistema. La Figura 1 contiene el diagrama de flujo y el sistema de ecuaciones diferenciales ordinarias que describen la dinámica vital de los hospederos humanos, vectores y sus valores son presentados en las tabla 1.
= FR x X, donde X es la variable de estado, t es el tiempo y FR es una tasa de incremento. Esta, puede ser constante o depender de otras variables del sistema. La Figura 1 contiene el diagrama de flujo y el sistema de ecuaciones diferenciales ordinarias que describen la dinámica vital de los hospederos humanos, vectores y sus valores son presentados en las tabla 1.
En la dinámica de transmisión del dengue se incluyen las tasas de incremento de las dos poblaciones, por ejemplo; el término μhH indica el número total de individuos de todas las edades y su sexo, que pueden contagiarse solo con una única cepa de virus y el tiempo medio de vida de un hospedero normal humano  es aproximadamente 68,5 años (Newton y Reiter 1992). Y para el vector está dado por γm M(1-w), que indica el número total de mosquitos (M = Sv + Ev + Iv), que se incrementa con una tasa γm, que es inferida a través de los resultados de Fantinatti et al. (2007). Esta tasa es el resultado de un proceso de colecta de huevos de A. aegypti en campo en algunas ciudades del Estado de Paraná en Brasil y su posterior cría en laboratorio.
es aproximadamente 68,5 años (Newton y Reiter 1992). Y para el vector está dado por γm M(1-w), que indica el número total de mosquitos (M = Sv + Ev + Iv), que se incrementa con una tasa γm, que es inferida a través de los resultados de Fantinatti et al. (2007). Esta tasa es el resultado de un proceso de colecta de huevos de A. aegypti en campo en algunas ciudades del Estado de Paraná en Brasil y su posterior cría en laboratorio.
El tiempo de vida medio el vector  fue estimado con base en nuestra experiencia con datos de cría por generaciones de A. aegypti en laboratorio (datos no publicados). Las tasas de contagio de los hospederos y vectores son los mismos del trabajo de Newton y Reiter (1992), representadas por el contacto de los hospederos susceptibles (Sh), con el vector infectado (Iv), relacionado con la tasa efectiva de contacto con el vector Cvh/M, que es determinada por la probabilidad de transmisión de un serotipo del dengue, hospedero vector (ahv) y la tasa de picadas (Sv) por día (bs), así Cvh = ahv bs .
fue estimado con base en nuestra experiencia con datos de cría por generaciones de A. aegypti en laboratorio (datos no publicados). Las tasas de contagio de los hospederos y vectores son los mismos del trabajo de Newton y Reiter (1992), representadas por el contacto de los hospederos susceptibles (Sh), con el vector infectado (Iv), relacionado con la tasa efectiva de contacto con el vector Cvh/M, que es determinada por la probabilidad de transmisión de un serotipo del dengue, hospedero vector (ahv) y la tasa de picadas (Sv) por día (bs), así Cvh = ahv bs .
El contagio del vector susceptible (Sv), representado por C H, que es determinado por la probabilidad de transmisión de un único serotipo del dengue del vector al hospedero (avh) y la tasa de picada de los (Iv) por día (bi), Chv = avh bs. Los parámetros que indican el control del vector (w) con el insecticida larvario Temefos (abate) e insecticidas para control del vector en el estado adulto (μma), son consideramos como una sumatoria de las acciones de control que son incorporadas al modelo de la siguiente forma: pérdida de potencia o ineficiencia del insecticida como resultado de la resistencia química a insecticidas, porcentaje de cobertura y actividades preventivas ejercidas por los humanos para control del vector (ejemplo, retirada permanente de criaderos potenciales efectuada por la población de forma espontánea). Se consideró la sumatoria de estos parámetros como de 100% de efectividad para demostrar la importancia de entender el control del vector como una acción múltiple de componentes que deben ser cuidadosamente planeados para no comprometer el control del mosquito.
Del sistema de ecuaciones diferenciales propuesto (Fig. 1) se obtiene que la población de mosquitos está dada por:

Donde, M0 es la población inicial de mosquitos. Se incorporó también una tasa de crecimiento del vector como función dependiente de la siguiente forma γm(t) = αexp [-b(A+Bcos(πt / 180) + Tmax)2] (Zotin et al. 1999), donde Tmax es la temperatura máxima (30°C), este parámetro es sugerido como el límite de temperatura para un desarrollo ideal del mosquito, de esta forma se simula el crecimiento continuo del vector, intentando que el crecimiento sea similar a temporadas de alta y baja producción de individuos, como es en condiciones naturales (Duque y Navarro-Silva 2006). La población del vector en el tiempo está dada por

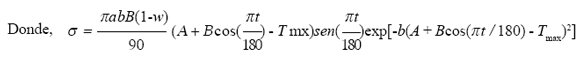
σ : indica la velocidad o variación de la tasa de crecimiento del vector, esto es, , donde
, donde
σ :  representa la variación de la población del vector en cada instante de tiempo t (mosquitos/día). Integrando la ecuación
representa la variación de la población del vector en cada instante de tiempo t (mosquitos/día). Integrando la ecuación
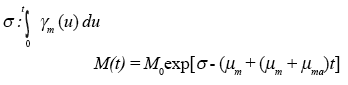
Donde,

Que nos representa la tasa de crecimiento de la población de mosquitos en el intervalo de tiempo [0, t].
Así obtenemos la tasa o número reproductivo básic R0 , dado por

R0 , es la tasa de casos secundarios de la infección del dengue producida por una persona infectada o mosquito infeccioso, depende del producto de los coeficientes de transmisión ChvCvh, esto es, un nuevo caso ocurre solo después de picar el mismo mosquito dos veces. El cual se deduce de las diferentes estrategias de control, si R0 < 1 la epidemia del dengue se extingue. El programa computacional para simular y validar el modelo fue Matlab 6.5 (The Mathworks tm.).
Resultados
En un brote de dengue la necesidad de control del vector es inminente y es primordial entender los alcances y el impacto de las estrategias destinadas a disminuir el evento epidémico. Para esto, fueron simulados los siguientes escenarios de transmisión: la transmisión del dengue sin ningún tipo de control en el vector (Fig. 2A), se caracteriza por la coexistencia del vector y hospedero, donde hay un incremento de los infecciosos (Ih) influenciado por el contacto con los vectores infecciosos (Iv), que decrece a través del tiempo por causa de la inmunidad adquirida al virus.
Ahora, pensando en la aplicación de acciones de control en el inicio de la epidemia, se consideró hipotéticamente una disminución de 70% de efectividad en (w) y 80% (μma) por pérdida de potencia, baja cobertura y poca remoción de criaderos del vector. Resulta que el número de mosquitos infectados (Iv) disminuye; sin embargo, el periodo epidémico se amplía en relación con la no aplicación de control en el vector (Fig. 2B). Esto puede explicarse en términos inmunológicos, donde hay baja inmunidad adquirida, porque el contacto con el vector disminuye.
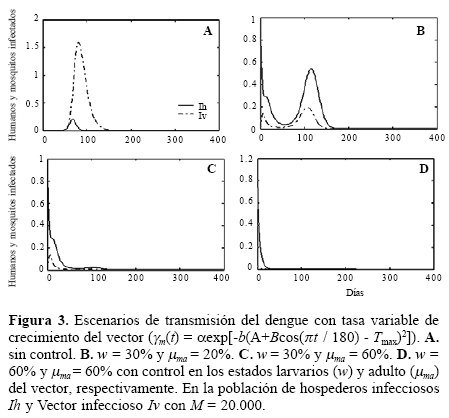
En la Figura 2C, se mantiene la disminución del 70% en (w), se disminuye también a 40% en (μma) y se observa cómo se controla la epidemia. Lo mismo pasa, si este porcentaje para (w) se mantiene con 40% (Fig. 2D). Estas figuras muestran que si fuera aplicado el control solo en las larvas, los adultos del mosquito en ese tiempo permanecen vivos, alimentándose y ovipositando, consecuentemente multiplicando su prole. Si solo se controlan los adultos, las larvas no tratadas restauran nuevamente la población, así un control más efectivo, será con una combinación entre el ataque entre los dos estados, reduciendo rápidamente la epidemia. Las acciones de control se complican si se contempla la posibilidad de resistencia al insecticida en los estados adultos. Utilizando la tasa de crecimiento del vector (γm) en función del tiempo se observa un comportamiento similar. La Figura 3A, tratamiento sin control, es igual a la 2A mientras que la 3B, se presenta como que el control de w y μma es más efectivo en la reducción del número de personas y mosquitos infecciosos Ih e Iv. Puede confirmarse también que el tratamiento en los adultos tiene más impacto en el número de casos que en las larvas (Fig. 3C y 3D).
Ahora, en la Figura 4, se muestra como la densidad del vector en el momento de control es fundamental para el control de la epidemia. En la Figura 2 fueron utilizados valores iniciales de M de 20.000 individuos, pero cuando se comparan en la Figura 4, con un M de 10.000 se observa como con las tasas destinadas al control consiguen disminuir rápidamente el brote epidémico, igualmente cuando se compara la Figura 3 con la 5. En vista de lo anterior, es indiscutible que es necesario evitar la epidemia estableciendo condiciones para mantener el menor número de individuos de relevo del vector, preferiblemente próximos a cero o considerar índices de infestación menores que 1%. Esto es posible si la tasa de incremento del vector es menor que la razón entre las tasas de mortalidad natural y control en el estado adulto entre la pérdida de efectividad del insecticida en el estado larvario, esto es,

Asimismo considerando el surgimiento de la resistencia a insecticidas, serán reducidos más rápidamente y en la secuencia también los hospederos infecciosos.
En relación con el Número Reproductivo Básico (R0) las estrategias de control del vector confirman que el control integrado en larvas y adultos debe ser aplicado al mismo tiempo para que haya una disminución real de la infección (Fig.6).
Discusión
La inclusión de los parámetros de control de larvas (w) y adultos (μma) en el modelo de Newton y Reiter (1992) abren la posibilidad de analizar y predecir circunstancias relacionadas a la aplicación de tratamientos diferenciados a larvas y adultos del vector A. aegypti, así como el análisis del impacto de las posibles combinaciones de estas variables en la reducción del vector y su influencia en la reducción de los casos del dengue. Otros aspectos que se observan en el modelo son las fallas en el control del vector, causadas por la resistencia y baja cobertura de las aplicaciones de insecticidas.
Se resalta que los parámetros destinados al control de larvas (w) y adultos (μma) son considerados como la sumatoria de varios eventos, como la resistencia a insecticidas, efectividad de cobertura de las aplicaciones de los insecticidas y las acciones permanentes de la comunidad en el control de criaderos del vector. La falla de alguno de estos parámetros compromete el control del vector, como se observa en la simulación. Dentro de esta lógica, es inútil el empleo de los insecticidas si no están cubriendo la totalidad de los criaderos, o si existen poblaciones resistentes.
Está comprobado que las aplicaciones de insecticidas UBV es afectada por factores como el refugio de las hembras y la migración a lugares libres de residuos químicos (Perich et al. 2000; Castro et al. 2007). De esta forma, el control integrado del vector, para ser efectivo, debe presentar una combinación de estrategias que eviten este fenómeno y faciliten el contacto directo con los insecticidas. En la actualidad son pocos los estudios que avanzan en esa dirección, sin embargo, algunas estrategias utilizando semioquímicos surgen como una forma sustentable para lograr una mejor cobertura de las aplicaciones de insecticidas (Navarro-Silva et al. 2009).
Así, como Burattini et al. (2008) afirmaron, observamos que la reducción más fuerte del número de enfermos de dengue se alcanza rápidamente con la reducción de los mosquitos en el estado adulto, cuando se compara con tratamientos destinados al control solamente de los estados larvales del vector. Esto implica que no se debe perder la potencia de los insecticidas para atacar el estado adulto, como se ha detectado en los piretroides como la cipermetrina en Cuba (Rodríguez et al. 1999), Brasil (Duque et al. 2004; Cunha et al. 2005) y la deltametrina en Perú (Chávez et al. 2005).
Como fue presentado en las simulaciones, en un evento epidémico la cantidad de individuos de relevo es crucial para la reducción rápida de la epidemia. Tal vez esto sea lo que pasa en las olas epidémicas. Normalmente, en una epidemia las acciones de control son aplicadas con vehemencia en la tentativa de frenar el aparecimiento de más personas infecciosas hasta conseguir en teoría el control de la enfermedad. Posteriormente, se observa un receso epidémico y posteriormente un brote igual o peor que el anterior (Duque 2008). Esto es consecuencia del impacto ejercido sobre las poblaciones del vector, que están sujetas a periodos de menor intensidad de control, permitiendo la dispersión y el aumento poblacional.
Dentro de las limitaciones del modelo podemos mencionar: no se especifica en cada uno de los serotipos de dengue (DEN 1, 2, 3 y 4), ni se abordan aspectos sobre la forma de trasmisión de las manifestaciones más graves de esta enfermedad (dengue hemorrágico). Tampoco es considerada una conexión entre espacio y tiempo que permita hacer predicciones puntuales en relación con una localidad específica; simplemente, porque nuestro interés actual es presentar los diferentes escenarios de control del vector y su influencia en la reducción de los casos de esta enfermedad en un evento epidémico. Con todo esto y a pesar de estas limitaciones, estimulamos a que las investigaciones sobre el control de A. aegypti estimen los parámetros y variables necesarios para validar esta propuesta en localidades específicas.
Se concluye que la inclusión de (w) tasa de control integrado y (μma) tasa de control en el estado adulto del vector en el modelo de Newton y Reiter (1992), abren la posibilidad de analizar y predecir circunstancias relacionadas con la aplicación de tratamientos diferenciados a las larvas y adultos de A. aegypti y su efecto en la epidemia de dengue. Esto no quiere decir que estemos invitando a el uso de insecticidas, todo lo contrario, estamos mostrando como esta estrategia puede influenciar una epidemia y también como su efecto en la reducción de los casos de dengue puede ser interpretado erradamente por el proceso de reducción de los casos por la inmunidad adquirida de la población. Llamamos la atención a que las estrategias esperanzadas en la utilización de insecticidas como único medio pueden solapar la realidad y su efecto apenas será complaciente por el simple acto de hacer una aplicación de un producto químico. Muchas son las variables que influencian el aumento de los casos de dengue y la falla en la ejecución de alguno de estos parámetros, indiscutiblemente compromete las acciones efectivas de combate del vector y también nos alerta que debemos conocer con antelación si los insecticidas han adquirido resistencia antes de la aplicación, especialmente si son dirigidos en los estados adultos.
Para finalizar, se debe tener en cuenta la relación densidad vector-hospedero pues es fundamental para el éxito de los programas de control, esto nos indica la necesidad urgente de implementar metodologías de vigilancia entomológica que detecten rápidamente la presencia del vector. Consideramos que es urgente incluir en los programas de control otros métodos complementares para el monitoreo de mosquitos como trampas para huevos y adultos.
Agradecimientos
Jonny E Duque L, agradece especialmente a CNPQ (Conselho Nacional de Desenvolvimento Científico e Tecnológico) en Brasil, por el apoyo brindado con la beca de doctorado en el periodo 2004-2008. Al Doctor Anibal Muñoz Loaiza Director Grupo de Modelación Matemática en Epidemiologia (GMME) de la Universidad del Quindío, Armenia, Quindío, Colombia por las valiosas sugerencias y aportes matemáticos al trabajo.
Literatura citada
BARTLEY, L. M.; DONELLY, C. A.; GARNETT, G. P. 2002. The seasonal pattern of dengue in endemic areas: Mathematical models of Mechanisms. The Royal Society of Tropical Medicine and Hygiene 96: 387 - 397. [ Links ]
BURATTINI, M. N.; CHEN, M.; CHOW, A.; COUTINHO, F. A. B.; GOH, K. T.; LOPEZ, L. F.; MA, S.; MASSAD, E.. 2008. Modelling the control strategies against dengue in Singapore. Epidemiology and Infection 136: 309-319. [ Links ]
CASTRO, M.; QUINTANA, N.; QUIÑONEZ, M. L. P. 2007. Evaluación de dos piretroides en el control del vector del dengue en Putumayo, Colombia. Revista de Salud Publica 9: 106-116. [ Links ]
CUNHA, M. P. da; LIMA, J. B. P.; BROGDON, W. G.; MOYA, G. E.; VALLE, D. 2005. Monitoring of resistance of resistance to the pyrethroid cypermethrin in Brazilian Aedes aegypti (Diptera: Culicidae) populations collected between 2001 and 2003. Memórias do Instituto Oswaldo Cruz 100: 441-444. [ Links ]
CHÁVEZ, J. C. G.; ROLDÁN, J. R.; VARGAS, F. V. 2005. Niveles de resistencia a dos insecticidas en poblaciones de Aedes aegypti (Diptera: Culicidae) del Perú. Revista Colombiana de Entomología 31: 75-78. [ Links ]
DEROUICH, M.; BOUTAYEB, A. 2006. Dengue fever: mathematical modeling and computer simulation. Applied Mathematics and Computation 177: 528-544. [ Links ]
DUQUE, J. E. L. 2008. Descrição e análise de fatores epidemiológicos, vetoriais e do controle da dengue no estado do Paraná, Brasil. Tese de doutorado. Programa de Zoologia, Curso de pós-graduação em entomologia. Universidade Federal do Paraná. Pag. 150. [ Links ]
DUQUE, J. E. L.; NAVARRO-SILVA, M. A. 2006. Dynamics of the control of Aedes (Stegomyia) aegypti Linnaeus (Diptera, Culicidae) by Bacillus thuringiensis var israelensis, related with temperature, density and concentration of insecticide. Revista Brasileira de Entomologia 50: 528-533. [ Links ]
DUQUE, J. E. L.; MARTINS, F. M.; ANJOS, F. A.; KUWABARA, E. F.; NAVARRO-SILVA, M. A. 2004. Susceptibilidade de Aedes aegypti aos inseticidas Temephos e Cipermetrina, Brasil. Revista de Saúde Publica 38: 842-843. [ Links ]
ESTEVA, L.; VARGAS, C. 1999. A model for dengue disease with variable human population. Journal of Mathematical Biology 28: 220-240 [ Links ]
ESTEVA, L.; VARGAS C. 2000. Influence of vertical and mechanical transmission on the dynamics of dengue disease. Mathematical Biosciences 167: 51-64. [ Links ]
ESTEVA L.; VARGAS C. 2003. Coexistence of different serotypes of dengue virus. Journal of Mathematical Biology 46: 31- 47. [ Links ]
FANTINATTI, E. C. S.; DUQUE, J. E. L.; SILVA, A. M.; NAVARRO- SILVA, M. A. 2007. Abundance and aggregation egg of Aedes aegypti L. and Aedes albopictus (Skuse) (Diptera: Culicidae) in the north and northwest of the State of Paraná, Brazil. Neotropical Entomology 36: 960-965. [ Links ]
GUBLER, D. J. 1998. Dengue and dengue hemorrhagic fever. Clinical Microbiology Reviews 11: 480-496. [ Links ]
HASTING, A. 1997. Population Biology. Concepts and Models. Springer-Verlag. New York, Inc. 220 p. [ Links ]
JOSHI, V.; MOURYA, D. T.; SHARMA, R. C. 2002. Persistence of dengue-3 virus through transovarial transmission passage in successive generations of Aedes aegypti mosquitoes. American Journal of Tropical Medicine and Hygiene 67: 158-161. [ Links ]
KROEGER, A.; NATHAN, M. B. 2006. Dengue: setting the global research agenda. The Lancet 368: 2193-2195. [ Links ]
NAVARRO-SILVA, M. A.; MARQUES, F. A.; DUQUE J. E. L. 2009. Review of semiochemicals that mediate the oviposition of mosquitoes: a possible sustainable tool for the control and monitoring of Culicidae. Revista Brasileira de Entomologia 53 (1): 1-6. [ Links ]
NEIL, M. F.; CHRISTL, A. D.; ROY, M. A. 1999. Transmission dynamics and epidemiology of dengue: Insights from age - stratified Sero - prevalence surveys. Philosophical Transactions of the Royal Society of London Biological Sciences 354: 757- 768. [ Links ]
NEWTON, E. A. C.; REITER, P. 1992. A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) insecticide applications on dengue epidemics. American Journal of Tropical Medicine and Hygiene 47: 709- 720. [ Links ]
PERIAGO, M. R.; GUZMÁN, M. G. 2007. Dengue y dengue hemorrágico en las Américas. Revista Panamericana de Salud Pública 21: 187-191. [ Links ]
PERICH, M. J.; DAVILA, G.; TURNER, A.; GARCIA, A.; NELSON, M. 2000. Behavior of resting Aedes aegypti (Culicidae: Diptera) and its relation to ultra-low volume adulticide efficacy in Panama City, Panama. Journal of Medical Entomology 37: 541-546. [ Links ]
PONGSUMPAN, P.; TANG, I. M. 2003. Transmission of dengue hemorrhagic fever in an age structured population. Journal Mathematical and Computer Modelling 37: 949 - 961. [ Links ]
RODRÍGUEZ, M. M.; BISSET, J. A.; MILÁ, L. H.; CALVO, E.; DIAZ, C.; SOCA, L. A. 1999. Niveles de resistencia a insecticidas y sus mecanismos en una cepa de Aedes aegypti de Santiago de Cuba. Revista Cubana de Medicina Tropical 51: 83-88. [ Links ]
ZOTIN, R. ; BASSANEZI, R. ; YANG, H. M. 1999. Controle ótimo da aplicação de Fungicidas em Áreas Lesionadas por Fungos. XXII Congresso Nacional de Matemática Aplicada e Computacional 22: 1-19. [ Links ]
Recibido: 28-jul-2008 - Aceptado: 23-ene-2009