ARTÍCULO ORIGINAL / ORIGINAL ARTICLE

Efecto de la conductancia de potasio Kv3.1 en la tasa y frecuencia de disparo de un axón no mielinado

Efect of the Kv3.1 potassium conductance in the firing frequency and firing rate of an unmyelinated axón

Oscar Emilio Hernández Bustos¹, Lilibeth Hernández Bustos²

¹ Docente del Departamento de Química y Biología de la Universidad del Norte. Barranquilla (Colombia). ohemandezb@uninorte.edu.co.

² Estudiante de Física, Universidad del Atlántico. Barranquilla (Colombia). mitalily@gmail.com.

Correspondencia: Oscar Emilio Hernández Bustos, Departamento de Química y Biología, Universidad del Norte, km 5, antigua vía a Puerto Colombia. Barranquilla (Colombia). ohernandezb@uninorte. edu.co, oscaremilio.hernandez@gmail.com.

Fecha de recepción: 9 de agosto de 2011

Fecha de aceptación: 12 de septiembre de 2011

Resumen

Objetivo: Determinar la relación entre la conductancia de potasio Kv3.1 y la tasa de disparo (Td) de un modelo neuronal llamado neurona1 formado por un soma, un cuello y un axón no mielinado durante un estímulo de corriente de 10 ms de duración y a 40°c.

Materiales y métodos: A partir del software libre neuron se simuló la propagación de ráfagas de potenciales de acción a través de neuronal, variando la conductancia específica máxima de potasio Kv3.1 (G_Kv31) relativa a la conductancia específica máxima de potasio (G_K) estudiada por a.l. Hodgkin y a.f. Huxley en 1952, de tal forma que G_Kv31+G_K=1.6S/ cm².

Resultados: En una estructura neuronal con las características biofísicas de neuronal, Td varía en forma sigmoidea para 0 < G_Kv31/G_K < 0.455 y decae exponencialmente para 0.455 < G_Kv31/G_K < 15, respectivamente. Para el primer caso, Td aumenta 11 veces más que la frecuencia (f) respecto del número de espigas en cada ráfaga.

Conclusión: La observación de la conductancia de potasio del tipo Kv3.1 en algún tipo de neurona no implica necesariamente la propagación de ráfagas de alta tasa de disparo. Su efecto es más pronunciado (11 veces) en la modulación de Td que en el aumento de f.

Palabras clave: Frecuencia de disparo, tasa de disparo, conductancia de potasio Kv3.1, axón no mielinado.

Abstract

Objective: To determine the relationship between the Kv3.1 potassium conductance and the firing rate (Td) in a neuronal model called neuron1, consisting of a soma, a hillock and an unmyelinated axon, during a constant current stimulus 10ms long and at 40°c.

Methodology: Using the free software neuron, the propagation of action potentials along a neuronal structure called neurona1 was simulated. The maximum Kv3.1 conductance (G_Kv31) relative to the maximum potassium conductance (G_k) studied in 1952 by a.l. Hodgkin and a.f. Huxley and in this paper called HH conductance, was varied such that G_k, +G_Kv3.1= 1.6s/cm2.

Results: In a neuronal structure with the biophysical characteristics of neuronl, Td varies in a sigmoid way for all g_kv31such that 0<G_Kv31/G_k< 0.455 and drops exponentially for all g_kv31such that 0.455<G_Kv31/G_k<15. For the first case, Td is 11 times greater than frequency rate (f) in respect to the number of spikes in every action potential burst.

Conclusion: The observation of Kv3.1 potassium conductance in some types of neurons does not necessary imply the propagation of high rate action potential bursts. Its effect is more pronounced (11 times) in the modulation of Td than in the increase off.

Keywords: Firing frequency, Rate frequency, Kv3.1 potassium conductance, Unmyelinated axon.

INTRODUCCIÓN

En la formación y propagación de potenciales de acción (PA) a través de una neurona están involucradas propiedades de conducción pasivas, como la capacitancia específica de membrana (c ), la resistencia interna o axial (Ri), la resistencia específica de membrana (r_m) y la conductancia específica de fuga, entre otras, y propiedades de conducción activas, entre las que se encuentran las conductancias correspondientes a canales voltaje-dependientes.

De especial interés en este trabajo son los canales de potasio voltaje-dependientes con inactivación del tipo Kv3.1, pertenecientes a la subfamilia Kv3 (1) y, por tanto, implicados en perfiles de descargas neuronales caracterizados por disparos repetitivos o ráfagas de potenciales de acción a altas frecuencias (2, 5). Esto último es conocido como el fenotipo "Fast Spiking" (FS).

En ese mismo orden de ideas, los canales Kv3.1 se activan (en un punto cercano al punto de máxima amplitud de la espiga) y desactivan (aproximadamente -70mV) durante la fase de repolarización, por lo cual, los PA en el fenotipo FS se caracterizan por su corta duración, rápida repolarización (al menos 10 veces más rápido que cualquier otro canal de potasio voltaje-dependiente), breves periodos refractarios e intervalos de posthiperpolarización y amplitudes sin decremento durante una ráfaga (3).

Estos patrones de descarga han sido observados en varios sectores del sistema nervioso central de algunas especies animales; entre estos, en el circuito atencional de aves (6), formado por el tectum óptico, los núcleos Imc, SLu y Ipc (7). En este último fueron detectados los canales Kv3.1 (7), respecto a los cuales puede presuponerse que existen también en el axón correspondiente (8).

En general, la cinética de apertura y cierre de un canal voltaje-dependiente depende de la temperatura (9-12), lo cual posibilita o no el ingreso y salida de la cantidad necesaria de cationes para la formación del PA. Esto es, a mayor temperatura, mayor rapidez de apertura y cierre, y a mayor rapidez de apertura y cierre, menor es el número de iones que pueden pasar a través de ellos hacia el interior o exterior celular. No obstante, las ecuaciones diferenciales que determinan las cinéticas de los canales pueden ser adaptadas para funcionar a cualquier otra temperatura (T), multiplicando las correspondientes tasas de apertura (a) y cierre (β) por el coeficiente térmico (9, 10,13):

Donde Q₁₀ es una medida del incremento de la velocidad de apertura y cierre de un canal iónico, cuando la temperatura aumenta en 10°C respecto de la temperatura de laboratorio T₀.

Para los canales de sodio y potasio voltaje-dependientes, estudiados en 1952 por Alan Lloyd Hodgkin y Andrew Fielding Huxley (14-18) a partir del axón gigante de calmar, y a los cuales nos referiremos en este artículo como "canales al estilo HH" (y a las conductancias correspondientes como, "conductancias al estilo HH"), Q₁₀=3 y T₀=6.3°C (9). Cabe resaltar que los canales Kv3.1 funcionan en el sistema nervioso de aves a 40°C (temperatura interna de las aves).

Una buena alternativa para estudiar la electrofisiología de los canales iónicos es la realización de simulaciones computacionales. Para esto existen varias herramientas; entre las cuales se puede destacar al software libre neuron (19, 22), que a diferencia de otros simuladores neuronales, como nest (23) y génesis (24), por mencionar algunos, tiene la capacidad de simular fenómenos asociados a una sola neurona con total control sobre sus características biofísicas y morfológicas individuales (25); esto se ve reflejado en la tendencia hacia el crecimiento del número de publicaciones (en revistas de reconocido prestigio en neurociencias) por año que usan esta plataforma (26).

Cabe agregar que neuron, por un lado, tiene incorporado, por defecto en su código raíz y en forma de archivos (.mod) en lenguaje de programación nmodl (27), la cinética de los canales de sodio y potasio al estilo HH y la correspondiente corrección de las tasas de apertura y cierre (Kα y kβ respectivamente) para adaptarlas a temperaturas diferentes de 6.3°C; entre estas, T = 40°C (28,29); por otro lado, existe una base de datos de software libres en lenguaje hoc y nmodl (30) que modelan la cinética de otros tipos de canales; entre estos, la de los Kv3.1 (31).

Para el estudio del fenotipo FS, a continuación se introducen, con significados particulares en este trabajo, los conceptos de tasa de disparo y frecuencia de disparo (ver figura 1).

Tasa de disparo (Td): Hace referencia al número de espigas de potenciales de acción (N) que se disparan durante un tiempo igual a la duración de un largo estímulo (t_est) (ver figura 1). Para su cálculo se empleará la siguiente fórmula:

Frecuencia de disparo (f): Es el número promedio de potenciales de acción (N) que se disparan durante el tiempo de duración de la ráfaga (t_bur). Se calcula de la siguiente forma:

Dado que t_est > t_bur, Td < f, para que Td = f, la ráfaga debe tener una duración de t_est ms.

Por todo lo anterior, el objetivo de este trabajo es determinar la relación entre la conductancia de potasio del tipo Kv3.1, relativa a la conductancia de potasio al estilo HH, y la tasa de disparo de un modelo neuronal formado por un soma, un cuello y un axón no mielinado, durante un estímulo de corriente de 10ms de duración y a 40°C de temperatura.

MATERIALES Y MÉTODOS

Como medio para probar los algoritmos y métodos desarrollados en este trabajo se realizó un modelo de estructura neuronal en lenguaje hoc (32), al que se llamó "neuronal", que reproduce en forma aproximada la morfología de las secciones: soma, cuello axonal y axón principal de las neuronas del núcleo Ipc de las aves (7, 8). No obstante, el interés principal de este trabajo se enfocó en el estudio del papel de los canales Kv3.1 en la propagación de ráfagas de potenciales de acción a través de un largo axón (2500 µm) y no en la realización de un modelo biofísico y morfológico funcional de las neuronas del Ipc. En general, a partir de simulación computacional con el software libre neuron se estudió, la respuesta del extremo distal de neuronal para T=40°, a un largo estímulo de corriente (pulso cuadrado) de 10ms de duración y 15nA de amplitud, aplicado en su extremo proximal (ver figura 2).

En concordancia con lo expresado en el párrafo anterior, las 3 secciones de neuronal comparten la misma biofísica, esto es, las mismas magnitudes para los parámetros de conducción pasivos y activos. Precisando de una vez, se mantuvieron constantes (con valores arbitrarios) para todas las simulaciones: la conductancia específica máxima de sodio al estilo HH (G_Na=4S/ cm²), la conductancia específica máxima de fuga (G_fuga=0.0004S/cm²: en código neuron, por defecto para un axón gigante de calamar, gl_hh=0.0003S/cm² sumado con g_ pas=0.0001S/cm²), Ri=40Qcm, c_m=1µF/cm², el parámetro de discretización nseg para el soma, el cuello axonal y el axón (nseg =1, nseg_cuello =1 y nseg_axon =250 respectivamente), el instante de tiempo al cual se aplicó el estímulo de corriente (t_del=2ms), el intervalo de tiempo para la realización del muestreo virtual (dt=0.0065ms) y los potenciales de equilibrio para el Na+ y K+ a +50mV y -83.1mV, respectivamente. Las conductancias específicas máximas de potasio al estilo HH (G_K) y Kv3.1 (G_Kv31) fueron variadas en cada simulación de tal forma que

Donde p_gk = G _Kv31 / G_K, esto es, conductancia específica máxima de potasio Kv3.1 relativa a la conductancia específica máxima de potasio al estilo HH. La constate 1.6 se escogió, debido a que para G_Kv31 + G_K >1.6 S/cm², se observa un comportamiento que no sigue la tendencia de los gráficos 1 y 2 (observándose 1 o 2 espigas), lo cual será materia de estudio en trabajo posteriores.

Gillies y David Willshaw el cual hace parte de los métodos del artículo "Membrane channel interaction underlying rat thalamic projection neuron rhythmic and bursting activity". Esta cinética incluye la corrección de las tasas de apertura y cierre a partir del coeficiente térmico k, esto es, ka y kβ, para Q₁₀=1.7 y T₀=32 (31, 33).

Por último, con el propósito de analizar las diferentes respuestas de neurona!, se realizaron a partir del software QtiPlot (34) los siguientes gráficos:

Tasa de disparo respecto de p_gk para los intervalos 0<p_gk<0.455 y 0.455<p_gk<15. En cada uno se ajustaron curvas que permitieron cuantificar la evolución de las variables Td y f con el incremento relativo de la conductanda específica máxima de potasio del tipo Kv3.1 respecto de la conductancia específica máxima de potasio al estilo HH, esto es: G_Kv3.1/G_K.

Tasa y frecuencia de disparo respecto del número de espigas de las ráfagas que dieron origen a los gráficos del ítem anterior, con el propósito de determinar la relación entre la aparición de nuevas espigas y la variación de Td y f.

RESULTADOS

En concordancia con la secuencia planeada en la sección de "Materiales y métodos", inicialmente se estudió la respuesta de neurona! (Td y f) a un largo estímulo de corriente de 10ms de duración y 15nA de amplitud. En el gráfico 1 se puede observar una relación sigmoidea entre la tasa de disparo del axón durante los 10ms de duración del estímulo y la razón p_gk=G_Kv3.1/G_K, para 0<p_gk<0.455. La curva ajustada corresponde a la función de Boltzmann:

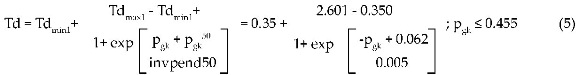
En esta ecuación podemos comprobar, en primer lugar, que el intervalo de valores posibles para Td es (0.350kHz, 2.601kHz) para p_gk (0, 0.455). Es importante resaltar que en una estructura neuronal con las características de neuronal, por más que aumente G_Kv31 respecto de G_K, la tasa de disparo no aumentará por encima de 2.601kHz, y por más que disminuya, esta tasa no será menor que 0.350kHz. En segundo lugar, para p_gk=0.062, inv.pend50=0.005 proporciona una medida del inverso de la pendiente de la recta tangente en el punto de inflexión (p Td50) = (0.062, 1.475kHz), donde Td=Td50 es el valor a mitad de rango. De este modo, si inv.pend50 fuese mayor, en este punto, la curva crecería con más lentitud y, por tanto, la variación de la tasa de descarga del axón con las características geométricas y de conducción similares a las de neuronal sería menor. Una variación de Ap_gk=0.003 causaría un aumento aproximado en la tasa de disparo de ATd=0.338kHz.

El significado de la constante inv.pend50 = 0.005 se puede determinar derivando la ecuación 4 y luego reemplazando p_gk=0.062; con esto obtenemos la ecuación (6).

Esto es, la máxima variación de la tasa de disparo de neuronal es 112.650kHz y se da cuando la conductancia específica máxima de potasio Kv3.1 es 0.062 veces mayor que la conductancia específica máxima de potasio al estilo HH.

A diferencia de la curva del gráfico 1, el gráfico 2 muestra una relación de decaimiento exponencial entre la tasa de disparo del axón de neuronal y p_gk para valores tales que 0.455<p_gk<15. La ecuación 7 se ajustada a esta curva.

A partir de esta ecuación se puede observar que para una conductancia específica máxima de potasio del tipo Kv3.1, 2.590 veces mayor que la conductancia específica máxima de potasio al estilo HH, la tasa de disparo del axón Td=1.680kHz es un 37% de TdR=2.021kHz. Este último es la amplitud del rango de valores de Td (desde 0.932kHz hasta 2.953kHz) respecto de la curva ajustada (ver gráfico 2).Td=2.953kHz (para p_gk=0) es un valor extrapolado a partir de la ecuación 7 (ver punto cuadrado en la parte superior del gráfico 2).

Hasta el momento solo hemos analizado la tasa de disparo de neuronal respecto de la proporción de conductancias específicas máximas de potasio p_gk. En el gráfico 3 se puede observar la relación entre la frecuencia y la tasa de disparo con el número de espigas en cada ráfaga (N), a partir de las cuales se realizó el gráfico 1 (algunas de éstas se pueden observar en el gráfico 4). A pesar de que en cada caso (ver gráficos 4A-E) se aprecia un aumento en el número de espigas en forma proporcional a G_Kv31, la variación de la tasa de disparo es aproximadamente 11 veces mayor que la variación de la frecuencia respecto de N (ver pendientes de las ecuaciones ajustadas 8 y 9 a las líneas 1 y 2 del gráfico 3 respectivamente). Esto es, el aumento en la conductancia específica máxima Kv3.1 respecto de G_K causa un incremento notorio en el número de espigas disparadas durante los 10ms (Td aumenta en 0.1kHz por cada nueva espiga en la ráfaga) de duración del estímulo y pequeños incrementos, apenas apreciables, en la frecuencia de las ráfagas (f aumenta en 0.009kHz por cada nueva espiga en la ráfaga).

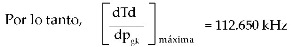
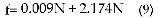
Por lo anterior, manteniendo constante la suma de conductancias específicas máximas de potasio G_K y G_Kv31 (ver ecuación 4) y variando solo la razón entre ellas, la frecuencia y la tasa de disparo de axones no mielinados (con propiedades de conducción similares a neurona!), durante el tiempo de duración de un largo estímulo (10ms) de 15nA de amplitud, varían en forma proporcional al número de espigas en cada ráfaga de PA y, por tanto, al aumento relativo (a G_K) de la conductancia específica máxima de potasio del tipo Kv3.1 (para 0<p_gk<0.455, ver gráfico 3).

En general, los resultados de los gráficos 1, 2, 3 y 4 ponen en evidencia, en forma novedosa, que el efecto principal de los canales de potasio del tipo Kv3.1 (para un intervalo de valores G_Kv3.1), más que dar paso a descargas de alta frecuencia, es permitir que se dispare un mayor número de espigas de potenciales de acción en un tiempo determinado, esto es, modular la tasa de disparo neuronal.

Las líneas ajustadas en el gráfico 3 (ver ecuaciones 8 y 9) se interceptan en el punto (23.699, 2.369). Es decir, cuando la ráfaga alcanza un número aproximado de 24 espigas, coinciden la tasa y la frecuencia de disparo. Esto se da cuando la actividad neuronal alcanza la máxima tasa de disparo que se puede alcanzar (ver gráfico 1) para una conductancia específica máxima Kv3.1 con respecto a la conductancia específica máxima de potasio al estilo HH.

DISCUSIÓN

Entre los resultados y aportes más importantes de este trabajo se pueden resaltar, en primer lugar, los gráficos 1 y 2, que constituyen una importante relación cuantitativa de la tasa de disparo de un axón no mielinado respecto de la razón entre las conductancias específicas máximas de potasio del tipo Kv3.1 y al estilo HH, para una estructura neuronal con características similares a neurona! y a una temperatura ambiente de 40°C. Estos gráficos muestran que la observación de conductancia de potasio del tipo Kv3.1 en una estructura neuronal no necesariamente significa que esta dé paso a la propagación de ráfagas de potencial de acción de alta frecuencia y/o tasa de disparo. Para el caso de una estructura neuronal con características similares a neuronal, la observación de ráfagas con alta tasa de disparo depende de la proporción p_gk=G_Kv31/G_K.

En segundo lugar, el gráfico 3 demuestra que el papel principal de la conductancia de potasio del tipo Kv3.1, más que facilitar la propagación de ráfagas de potencial de acción de alta frecuencia, es posibilitar su propagación con un mayor número de espigas, es decir, causar un incremento (modular) en la tasa de disparo neuronal (ver ecuaciones 8 y 9).

En general, todos los resultados de este trabajo constituyen un elemento de juicio para que, a partir de registros experimentales, se presuponga o no la existencia de canales del tipo Kv3.1 en membranas neuronales, con miras al desarrollo de modelos funcionales, teóricos y computacionales que expliquen la forma de un tipo de descarga de espigas de potenciales de acción en ráfaga.

Este trabajo puede ser extendido explorando la respuesta de neurona! a diferentes temperaturas, buscando si existe o no algún tipo de relación entre esta y la forma de las curvas Td vs. p_gk correspondientes, además de la relación entre la frecuencia de disparo y p_gk. También se podría estudiar la forma como se relacionan la pendiente de las líneas ajustadas en el gráfico 3 con T.

CONCLUSIONES

La variación de la tasa de disparo respecto de la proporción (p) entre las conductancias específicas máximas de potasio del tipo Kv3.1 y al estilo HH en neuronas con una biofísica similar a la de neurona! aumenta en forma sigmoidea para p_gk < 0.455 y decae exponencialmente para p_gk>0.455, es decir:

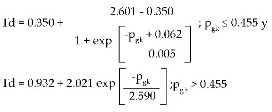
Estas ecuaciones demuestran que la magnitud de la conductancia Kv3.1 no siempre es proporcional a la tasa de disparo neuronal. Un axón con mayor conductancia de potasio, del tipo Kv3.1, que otro no siempre da paso a una mayor tasa de descarga. La observación de ráfagas con alta tasa de disparo en estructuras neuronales con características de conducción similares a neurona! depende de la proporción p_gk=G_Kv31/G_K.

Los canales de potasio del tipo Kv3.1 pueden dar paso (para 0<p_gk<0.455) al aumento en el número de espigas de potencial de acción presente en una ráfaga, es decir, incrementar la tasa de disparo neuronal. Este incremento, para una estructura neuronal con las características de neurona!, es aproximadamente 11 veces más grande que el correspondiente a la frecuencia de disparo respecto del número de espigas en cada ráfaga, lo cual se puede observar en las pendientes de las ecuaciones Td = 0.100N y f = 0.009N+2.174, es decir, el efecto principal de los canales de potasio del tipo Kv3.1, más que dar paso a descargas de alta frecuencia, es modular la tasa de disparo neuronal.

Conflicto de intereses: Ninguno.

Financiación: Universidad del Norte.

REFERENCIAS

(1) Miller C. An overview of potassium channels family. Genome Biology 2000; 1(4): 1-5.        [ Links ]

(2) Gan L, Kaczmarek LK. When, Where, and How Much? Expression of the Kv3.1 Potassium Channel in High Frequency Firing Neurons. Developmental Neurobiology 1998; 37: 69-79.        [ Links ]

(3) Rudy B, McBain CJ. Kv3.1 channels: voltage - gated K+ channels designed for high - frequency repetitive firing. Trends in Neurosciences 2001; 24(9): 517 - 526.        [ Links ]

(4) Wang LY, Gan L, Forsythe ID, Kaczmarek LK. Contribution of Kv3.1 potassium channel to high-frequency firing in mouse auditory neurons. Journal of Physiology 1998; 509(1): 183-194.        [ Links ]

(5) Bean BP. The action potential in mammalian central neurons. Nature Reviews 2007; 8: 451 - 65.        [ Links ]

(6) Marin G, Mpodozis J, Sentis E, Ossandon T, Letelier JC. Oscillatory busts in the optic tectum of birds represent re-entrant signals from the nucleus isthmi pars parvocellularis. Journal of Neuroscience 2005; 25 (30): 7081-89.        [ Links ]

(7) Wang Y, Luksch H, Brecha NC, Karten HJ. Columnar projections from the cholinergic nucleus isthmi to the optic tectum in chicks (Gallus gallus): A possible substrate for synchronizing tectal channels. The Journal of Comparative Neurology 2006; 494: 7-35.        [ Links ]

(8) Hernández O. Simulación de la propagación del potencial de acción en geometrías complejas: Aplicación al circuito atencional itsmo - tectal de aves. [Tesis]. Santiago de Chile; 2009.        [ Links ]

(9) Fitzhugh R. Theoretical effect of temperature on threshold in the Hodgkin-Huxley nerve model. The Journal of General Physiology 1966; 49: 989 -1005.        [ Links ]

(10) Rattay F, Aberham M. Modeling Axon Membranes for Functional Electrical Stimulation. ieee Transactions on Biomedical Engineering 1993; 40(12): 1201- 9.        [ Links ]

(11) Somero G. Temperature Adaptation of Enzymes: Biological Optimization Through Structure-Function Compromises. Annual Review of Ecology and Systematics 1978; 9: 1- 29.        [ Links ]

(12) Hodgkin A, Katz B. The effect of temperature on the electrical activity of the giant axon of the squid. Journal of Physiology 1949; 109: 240-9.        [ Links ]

(13) Plonsey R, Barr RC. Bioelectricity: A quantitative approach. 3^a ed. New York, USA: Springer; 2007.        [ Links ]

(14) Hodgkin A, Huxley A, Katz B. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. Journal of Physiology 1952; 116: 424-48.        [ Links ]

(15) Hodgkin A, Huxley A. Currents carried by sodium and potassium ions. Journal of Physiology 1952; 116: 449-72.        [ Links ]

(16) Hodgkin A, Huxley A. The components of membrane conductance in the giant axon of Loligo. Journal of Physiology 1952; 116: 47396.        [ Links ]

(17) Hodgkin A, Huxley A. The dual effect of membrane potential on sodium conductance in the giant axon of Loligo. Journal of Physiology 1952; 116: 497-506.        [ Links ]

(18) Hodgkin A, Huxley A, Katz B. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology 1952; 117: 50044.        [ Links ]

(19) Hines M, Carnevale N. neuron: a Tool for Neuroscientists. The Neuroscientist 2001; 7: 123-35.        [ Links ]

(20) Hines M, Carnevale N. Discrete event simulation in the neuron environment. Neurocomputing 2004; 58-60: 1117 - 22.        [ Links ]

(21) Hines M, Carnevale N. The neuron Book. Cambridge: Cambridge University Press; 2005.        [ Links ]

(22) NEURON for empirically-based simulations of neurons and networks of neurons. Disponible en: http://www.neuron.yale.edu/neuron/. [Consultado el 10 de mayo de 2011].        [ Links ]

(23) NEST initiative. Disponible en: http://www.nest-initiative.org/index.php/. [Consultado el 10 de mayo de 2011].        [ Links ]

(24) GENESIS Sim.org. Disponible en: http://genesis-sim.org/. [Consultado el 17 de mayo de 2011].        [ Links ]

(25) Hines M, Carnevale N. The NEuRoN Book. Cambridge: Cambridge University Press; 2005. p. 1-31.        [ Links ]

(26) Research reports that have used neuron. Disponible en: http://www.neuron.yale.edu/neuron/static/bib/usednrn.html. [Consultado el 10 de mayo de 2011].        [ Links ]

(27) Hines ML, Carnevale NT. Expanding neuron's Repertoire of mechanism with nmodl. Neural Computation 2000; 12: 839851.        [ Links ]

(28) Archivo .mod que modela la cinética de los canals de potasio al estilo HH. Disponible en: http://www.neuron.yale.edu/svn/neu-ron/nrn/trunk/share/demo/release/khh-chan.mod. [Consultado el 10 de mayo de 2011].        [ Links ]

(29) Archivo .mod que modela la cinética de los canals de sodio al estilo HH. Disponible en: http://www.neuron.yale.edu/svn/neuron/nrn/trunk/share/demo/release/nachan. mod. [Consultado el 10 de mayo de 2011].        [ Links ]

(30) ModelDB. Disponible en: http://senselab.med.yale.edu/modeldb/. [Consultado el 10 de mayo de 2011].        [ Links ]

(31) Archivo .mod que modela la cinética de los canals de potasio Kv3.1. Disponible en: http://senselab.med.yale.edu/modeldb/showmodel.asp?model=74298&file=\sth-model\Kv31.mod. [Consultado el 10 de mayo de 2011].        [ Links ]

(32) Hines M, Carnevale N. The neuron Book. Cambridge: Cambridge University Press; 2005. p. 343-362.        [ Links ]

(33) Gilles A., Willshaw D. Membrane channel interactions underlying rat subthalamic projection neuron rhythmic and bursting activity. Journal of Neurophysiology 2006; 95: 2352-2365.        [ Links ]

(34) QtiPlot - Data Analysis and Scientific Visualisation. Disponible en: http://soft.proin-dependent.com/qtiplot.html. [Consultado el 10 de mayo de 2011].        [ Links ]