Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.53 Medellín July/Sept. 2010
Strategy based on genetic algorithms for an optimal adjust of a support vector machine used for locating faults in power distribution systems
Estrategia basada en algoritmos genéticos para el ajuste óptimo de una máquina de soporte vectorial utilizada para localización de fallas en sistemas de distribución de energía eléctrica
Jaime Gutiérrez Gallego, Juan Mora Flórez*, Sandra Pérez Londoño
Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad (ICE3). Pereira, La Julita, Universidad Tecnológica de Pereira, Programa de Ingeniería Eléctrica. Pereira, Colombia.
Abstract
This paper presents a hybrid alternative to obtain a low computational cost strategy used to adjust the parameters of a Support Vector Machine based fault locator. The proposed strategy to determine the best parameters is based on the Chu Beasley Genetic Algorithm. The fault locator is tested in the IEEE 34 bus feeder, using a database of 2,180 registers of single phase, phase to phase, double phase to ground and three phase faults, obtained from simulation in ATP and Matlab. As results, the best alternatives for all of these four types of faults give an average cross validation error of 0.3%.
Keywords: Classification, fault location, genetic algorithms, power distribution systems and support vector machines
Resumen
En este artículo se presenta la selección de los parámetros de un localizador de fallas basado en máquinas de soporte vectorial, utilizando una estrategia híbrida de bajo costo computational fundamentada en el algoritmo genético de Chu Beasley. El localizador propuesto se prueba en el sistema de distribución IEEE de 34 nodos, donde los resultados muestran errores de validación cruzada promedio para las mejores alternativas de 0,3%, considerando los casos analizados con una base de datos de 2.180 registros fallas monofásicas, bifásicas, bifásicas a tierra y trifásicas. La base de datos de prueba se obtiene mediante simulación con ATP y Matlab.
Palabras clave: Algoritmos genéticos, clasificación, localización de fallas, máquinas de soporte vectorial y sistemas de distribución de energía eléctrica
Introduction
Frequent shunt faults cause supply interruptions that are responsible of poor continuity indexes affecting the quality of power. Fault locators help to reduce the effect on the frequency and duration indexes in three ways: First, fault location helps to speed up the restoration process; second, by locating the fault it is possible to perform switching operations to reduce the faulted area, and finally, location of non permanent faults possibilities scheduled maintenance tasks to avoid future faults [1, 2, 3].
Very good approaches have been proposed for locating faults in power transmission systems, but these algorithms are not useful in radial systems, specifically in distribution systems due to some distinctive characteristics of the last, such as: a) single end measurements; b) presence of single and double phase laterals; c) variable tapped loads; and d) lines with heterogeneous sections (different conductor gauges, overhead lines and underground cables, among others) [1, 3, 4].
Fault location in power distribution systems is mainly based on methods which use the impedance calculation during fault situation, as seen from the substation. The main disadvantages are associated to the multiple estimation of the fault location and the high model dependency [4, 5, 6]. On the other hand, many researchers have recently addressed the fault location problem using knowledge- discovering techniques, based on exploiting the existence of previous experiences and contextual information. In Mescal et al. [7] an approach to locate faults in power distribution systems using Neuronal Networks (NN) is proposed but, the multiple estimation problem is not analyzed. Additionally, an approach which uses Support Vector Machines (SVM) and NN to determine the fault distance is proposed by Thukaram et al. [8], where the multiple estimation problem is considered by patrolling the protective devices located along the feeders. Finally, G.Morales et al. [9] use a learning algorithm based on SVM to locate faults, but despite of the good results, the setting process depends of an extensive test which is computationally expensive, considering the search space given by the infinite interval of the classifier parameters (two real and positive numbers).
According to the above described, this paper is oriented to use the fault databases to determine the zone of the fault, avoiding the multiple estimation problem. The fundamental idea is to use the SVM as a classification technique (SVM-c) to obtain the zone at the power system where a fault is located. Additionally, the Chu Beasley Genetic Algorithm (CBGA) is used to determine the optimal set of configuration parameters of the SVM-c, for 15 possible combinations of descriptors used as inputs. The proposed descriptors are the variations of voltage, current, apparent power and system reactance, obtained from measurements of voltage and current in the fault database.
Basic fundamental aspects
One of the learning algorithms to data analysis is the SVM, which is based on quadratic programming, several clearly defined constrains and kernel transformations. The setting parameters of the SVM could be selected based on the prior knowledge of the user, but normally, it is not an optimal solution, and it is the main reason why the Genetic Algorithms (GA) are here also used. Considering the previoully explained, this section is devoted to present the basis of these two techniques, where several bibliographical references are used, because a detailed explanation about such techniques is out of the scope of this paper. Useful references for SVM and GA are presented in [10, 11, 12, 13].
Support vector machines used for classification (SVM-c)
SVM-c are based in the statistical learning theory and can be viewed as a binary classification technique, resulting from the development of NN and its combination with the optimization, kernel and generalization theories [10, 11].
Linear case
Having n training elements xi. in a N dimensional space, each element has its respective label y to designate members of the same class (+1 or -1) as it is presented in (1).
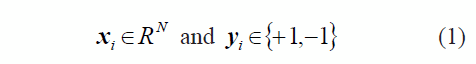
The goal is to find an optimal separation hyperplane (OSH) H:y=w.x+b=0, which has the maximum margin to the training nearest pattern, forcing the generalization of the learning machine as in figure 1 [11]. Weight (w) and bias (b) control the function and those data points that the margin pushes up against are called "support vectors" (k, l, m and n).
Figure 1 Separating hyperplanes
To find the OSH is necessary to solve the optimization problem presented in (2), considering that margin is inversely proportional to (w.w)1/2.

Soft margin
The previously presented is based on the non existence of mixed classes. To cope with this circunstance, the strategy is reformulated by considering relaxation variables (ξ) in the optimization problem to define what is known as a "soft margin". Thus, the optimization problem presented in (2) is now given as (3), where C is the error penalization constant.
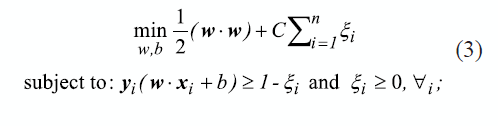
Kernel based SVM-c
In the case of non-linear separable feature sets, it is possible to transform the input into a new higher dimension space, where the data is linearly separable. The transformation function F(.) is defined in terms of inner products of the input data in the original classification space. Thus, it is not necessary to specify F(.); instead of it, kernel functions are used to perform the transformation and the inner product in the transformed space in a single step. Linear classification algorithms can be extended to non-linear cases by using an appropriate kernel function [10]. When a Radial Basis Function (RBF) is chosen as kernel function, two SVM-c parameters (constant C and kernel parameter s) have to be determined.
Chu Beasley Genetic Algorithms (CBGA)
A GA is a well known technique used to find exact or approximate solutions to optimization and searching problems. These algorithms are categorized as global hyper-heuristics search and are a particular class of evolutionary algorithms that use techniques inspired by biology such as inheritance, mutation, selection and crossover [12].
GAs are implemented as a computer simulation in which a population of abstract representations (chromosomes or the genotype of the genome) of solution candidates (individuals) to an optimization problem evolves toward better solutions. The evolution usually starts from a population of randomly generated individuals and happens in periods which are called as generations. In each generation, the fitness of every individual in the population is evaluated; multiple individuals are stochastically selected from the current population based on their fitness, and modified to obtain a new population. This last population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population.
The CBGA is a modified version of the basic GA oriented to maintain the diversity among the population individuals. It is an elitist algorithm considering that a parent is replaced by a descendent if and only if the last has a better objective function. In addition, each one of the population individuals have to be different from the other individuals (diversity), avoiding the premature convergences to local suboptimal solutions. Figure 2 shows a basic representation of the CBGA functioning [13].
Additionally an aspiration criterion is considered for including an individual which did not met the diversity, if and only if this objective function is better than the best of the population. In this case, all the individuals which not meet the diversity criterion, considering the new member included by the aspiration criterion, have to be removed. All of the removed members have to be replaced in the next generation, to maintain constant the population size. CBGA only changes a single individual in each generation while the basic approach modifies the entire population.
Figure 2 Chu-Beasley algorithm basic functioning
Proposed hybrid fault location approach
Most of the power distribution utilities have installed event recorders but do not have enough of automatic strategies to handle the stored information and as a consequence it is not adequately used causing a not effective improvement process [14]. The basic structure of the proposed approach is oriented to use all of the information stored in databases for locating the faulted zone. The core of the locator is the SVM-c, the inputs are usually called descriptors which corresponds to the information obtained from the currents and voltages stored in the fault database, and finally, the configuration parameters are selected by using a searching technique as the CBGA.
Methodology
The proposed strategy consists on four stages which are presented in figure 3. It is devoted to iteratively test several SVM-c configuration parameters proposed by the CBGA until the optimal configuration is obtained. The SVM-c configuration parameters are two, the penalization constant C and the parameter s considering a RBF kernel.
Figure 3 Four stages strategy to develop a SVM-c based fault locator
Stage I. Input data adjustment
This stage is subdivided in three steps and it is mainly devoted to adjust the measurements of voltage and current at the power substation.
Step one. Data handling
It is oriented to subdivide the power distribution system to determine which nodes belong to each class (zone). This helps the assignation process which relates the faults and the zones.
Having correlated the fault registers with the respective zone, a characterization of the measurements of voltage and current is proposed to obtain descriptors used as input training set of the fault locator. A set of descriptors based on the variations of the fundamental component of current and voltage are then obtained. Variations of the fundamental component of phase current (ΔI), phase voltage (ΔV), phase reactance (ΔX) and apparent power (ΔS) are proposed as descriptors. These are defined as the subtraction of rms values during the fault and pre-fault steady states [9]. As basic information, variations at the three phases are used as descriptors, to consider the distance of the fault, fault type, mutual coupling and the fault resistance influences.
Step two. Normalization of descriptors
The training set is normalized to avoid miss adjustments caused by high variations on the descriptor values. This normalization is in the interval [0, 1] as proposed in (4).

Step three. Diversification
This step is oriented to distribute adequately the training data (descriptors) and then subdivide it in v subsets. These subsets are later used in v-fold cross validation and that is the reason of why each of the subsets requires information related to faults located in each one of the zones proposed for the analyzed power system.
Stage II. Genetic algorithm for adjustment the SVM-c parameters
The proposed CBGA has a similar structure of a basic GA. The main differences are two: a) only one of the individuals is changed on each iteration, and b) all the individuals have to maintain a diversity degree to assure a correct coverage of the solution space. The steps to develop the proposed algorithm are following presented.
Step one. Coding and scaling
The proposed genetic algorithm possibilities a coding strategy using binary, integer real variables, depending on the problem needs. In this specific case where the parameter values are real numbers, the codification is performed by the definition of an interval of E and F real and positive numbers, uniformly distributed in the solution space for C and s parameters, respectively.
According to previous studies, the solution space in this type of problems is defined by the interval 24<C<230 and 2-6<σ<26 [15]. Finally, the population or solution alternatives is then given by each one of the individuals, defined by the ordered pair of SVM-c parameters (C,σ).
Step two. Initial population
In most of the cases, the CBGA starts an iterative process by generation of an initial population using random approaches. In the proposed approach, this strategy is complemented by the deterministic addition of some individuals considered as feasible and quasi optimal solutions.
Step three. Selection
Although in the classical references there are proposed several parent selection alternatives, in this approach the tournament selection is picked [13]. This basically consists in a selection of the alternative which has the best objective function from the k individuals randomly selected. The value of k could varies depending on the size of the population and then according to the problem of fault location a value of k=2 is selected. Then two tournaments are used to select the two parents which are used in the following step.
Step four. Crossover
Having selected two parents, the following step is combining them to obtain two descendents. In the crossover process, it is necessary to define the gen where it is performed and considering that the individual has only two positions (C and σ), the process is simple by the randomly selection of one them. Although normally it is defined a crossover probability rate, in this specific approach it is not defined, due the reduced size of the individual (two gens). As results, two descendents are obtained and only one is randomly selected and next used.
Step five. Mutation
In this approach, the mutation is defined by the variation in one of the two gens randomly selected. This variation consist in the addition or subtraction of a randomly quantity which is in the interval determined by a predefined percentage of the maximum possible value of the gen.
Step six. Decision criterion
Considering the proposed coding strategy used in the approach, the new descendent could substitute the individual which has the worst objective function if and only if the descendent has better objective function and meets the diversity criterion.
Stage III. Training the SVM-c
Defined structure of the SVM-c
As presented in section two, basic SVM-c is oriented to a bi-classification scheme, but the problem of fault location in power distribution systems is a multi-classification approach. In order to solve this problem is necessary to use the generalization of the SVM-c by defining a global classification function from a set of bi-classification functions, using decomposition and reconstruction strategies. The selected decomposition technique is one versus one and the simple voting is the reconstruction technique here used [10, 11].
Objective function definition as the classification error
Using a set of descriptors as inputs of the SVM-c as it was described in the stage I, and one of the individuals of the population defined by the CBGA presented in the stage II to set the parameters C and σ, the training stage is started. These all stages are devoted to obtain the best configuration parameters, determined by the minimum cross validation error in the faulted zone estimation.
Considering that it is not known beforehand which parameters are the best for the SVM-c, consequently the model selection (parameter evaluation) has to be done using cross validation. In v-fold cross-validation, first a subdivision of the training set into v subsets of equal size is performed. Sequentially each subset is tested using the SVM-c trained on the remaining v-1 subsets. Thus, each instance of the whole training set is predicted once, so the cross-validation error is estimated as it is presented in (5). T is the number of fault data in each subset, (v-fold)* T is the total training faults using in this stage and j identifies the evaluated individual.

Stage IV. Error evaluation and optimal parameters
15 different input sets are obtained from the combination of the four basic descriptors presented in stage I (ΔI, ΔV, ΔX and ΔS). For each one of these sets, the optimal values of the SVM-c parameters are obtained by using the CBGA and by the definition of the objective function as the minimization of the cross validation error in equation (5). Once the stop criterion of the genetic algorithm is reached, the best parameters are those which give a lower error.
Test and result analysis
Power distribution system used in tests
The 24.9 kV IEEE 34-bus feeder presented in figura 4 is used to test the fault location approach [16]. The proposed system contains a three phase main feeder, single-phase laterals, multiple conductor gauges, single and three phase tapped loads.
Figure 4 IEEE 34-bus test feeder
Description of the tests
The fault location defined as a classification problem, requires of a zone definition of the analyzed circuit which is presented in figure 4. The dataset used in the v-fold validation process considers 660 single phase faults, 570 phase to phase faults, 570 double phases to ground faults and 380 three phase faults. The used descriptors or inputs of the SVM-c are defined by the set composed of the 15 possible combinations of ΔI, ΔV, ΔX and ΔS.
For testing, an initial CBGA population is composed by 30 individuals, a 4-fold cross validation is used and the values of the integer constants to define the search space are defined as E=F=500.
Results
As result of the combination of the GA and the cross validation strategy, the best SVM-c parameters in the case of each one of the 15 defined set of descriptors and for four different fault locators are obtained. Table 1 presents the best SVM-c configuration parameters.
Table 1 Best SVM-c configuration parameters obtained using a CBGA and cross validation
The SVM-c adjusted using the parameters presented in table 1 is tested in a 4-fold cross validation process. The error estimated as in equation (5) is presented in table 2.
According to the results presented in table 2, the cross validation errors are small and variant depending of the set of descriptors used as inputs. In such tests were only one descriptor is used as input, the errors are relatively high, especially in the case on single phase, phase to phase and double phase to ground faults (maximum error of 16.6%). However if more than one descriptor is used as input, errors drastically decrease in most of the cases. In the case of three phase faults, it is notice how in the most of the tested circumstances the cross validation error is zero. As a summary, the best alternatives for all of the four types of faults (these highlighted using bolded numbers in table 2) give an average cross validation error of 0.3%. These results offer an interesting alternative for adjusting and selecting the descriptors at the input on the SVM-c, in order to reach a very good performance in the proposed situation.
Table 2 4-fold cross validation errors obtained in the faulted zone location using a SVM-c
Analysis
A simple strategy to determine the error nature and as a consequence the performance of the SVM-c is called confusion matrix, which simply relates the real faulted zone location and those faulted zones determined by the locator. As a consequence, a perfect prediction is obtained in the case of having a diagonal confusion matrix, which means that all of the data corresponding to a specific zone is located in the same zone by the proposed SVM-c locator. Table 3 shows the confusion matrix in the case of single phase faults, considering the best result obtained which is presented in table 2. In addition also in table 3 and in parenthesis, the confusion matrix in the case of single phase faults, considering the worst result obtained is given.
In the case of zero error which is obtained in the best case, the confusion matrix is completely diagonal, as it is presented in table 3
In the worst case for the single phase fault locator the highest cross validation error is 6.21%, and according to table 3 (on parenthesis) it is noticed how 41 faults of 660 single phase faults are wrong classified or recognized in a different faulted zone. All of the faults which are not recognized in the real faulted zone were recognized in a closest neighboring zone and these are outside of the diagonal and also on parenthesis. As example, there are 110 faults in zone four but only 102 of them were recognized in this real zone, 5 in zone three and 3 in zone six. Zones three, four and six correspond to neighboring parts of the power distribution system. All of the errors are due to faults which really belong to a zone, but are located in a neighboring zone, according to the system division presented in figure 4. The last circumstance evidences the necessity for defining an additional index to the proposed in (5), to give a confidence degree which helps to solve the problem of wrong classified faults; then this aspect is evidenced as a further research.
Table 3 Confusion matrix in case the best (worst) results obtained for the single phase fault locator presented in table 2
Finally and as a comparison of the obtained methodology and the proposed in [15], in this reference an extensive test is performed by the definition of a feasible interval of C and σ and all of the individuals (C, σ) in this interval are tested. In The proposed approach a guided search is performed avoiding the extensive tests and additionally having obtained better results.
Conclusions
This paper proposes a straightforward strategy which uses a Chu Beasley Genetic Algorithm for performing an oriented search in the optimization space, aimed to select the best parameters of a SVM-c based fault locator. The strategy is oriented to test each one of the population individuals from the genetic algorithm in the SVM-c and the cross validation error is then defined as objective function. The genetic algorithm evolves until the lowest cross validation error is obtained. This strategy is repeated to consider 15 different set of descriptors at the SVM-c input.
Additionally, several tests were presented considering four different fault locators according to the possible types of shunt faults in power distribution systems. The results show perfect performance in case on single, double phase to ground and three phase faults, and a minimum error of 1.05% in the case of phase to phase faults, considering test in the IEEE 34 bus feeder.
Finally as it was demonstrated, the proposed approach contributes to improve the power continuity indexes in distribution systems, by the opportune zone fault location.
References
1. IEEE Std 37.114. IEEE Guide for Determining Fault Location on AC Transmission and Distribution Lines. Power System Relaying Committee. 2004. pp. 1-36. [ Links ]
2. T. Short. Electric Power Distribution Handbook. CRC press. New York. Vol. 1. 2003. pp. 8-30. [ Links ]
3. J. Mora, G. Carrillo, B. Barrera. "Fault Location in Power Distribution Systems Using a Learning Algorithm for Multivariable Data Analysis". IEEE Transaction on PowerDelivery.Vol. 22. 2007. pp. 1715-1721. [ Links ]
4. J. Mora-Florez, J. Meléndez, G. Carrillo-Caicedo, "Comparison of impedance based fault location methods for power distribution systems," Electric Power Systems Research. Vol. 78. 2008. pp. 657-666. [ Links ]
5. K. Srinivasan, A. St-Jacques. "A new fault location algorithm for radial transmission lines with loads". IEEE Transactions on Power Delivery. Vol. 4. 1989. pp. 1676-1682. [ Links ]
6. A. Girgis, C. Fallon, D. Lubkeman. "A fault location technique for rural distribution feeders" IEEE Transactions on Industry and Applications. Vol. 26. 1993. pp. 1170-1175. [ Links ]
7. A. Mescal, A. Al-Shaher, S. Manar. "Fault location in multi-ring distribution network using artificial neural network". Electric Power Systems Research. Vol 64. 2003. pp. 87-92. [ Links ]
8. D. Thukaram, H. Khincha H. Vijaynarasimha "Artificial Neural Network and Support Vector Machine Approach for Locating Faults in Radial Distribution Systems". IEEE Transactions on Power Delivery. Vol. 20. 2005. pp. 710-721. [ Links ]
9. G. Morales, J. Mora, S. Pérez. "Learning-based strategy for reducing the multiple estimation problem of fault zone location in radial power Systems" IET Generation, Transmission and Distribution. Vol. 3. 2009. pp. 346-356. [ Links ]
10. C. Burges. A tutorial on Support Vector Machines for Pattern Recognition. http://www.kernel-machines.org/. Consultada el 15 de septiembre de 2008. [ Links ]
11. S. Bernhard, S. Alex. Learning with Kernels Support Vector Machines, Regularization, Optimization and Beyond. Ed. MIT Press. Cambridge. 2002. pp. 24-69. [ Links ]
12. A. Eiben, J. Smith. Introduction to Evolutionary Computing (Natural Computing Series). Ed. Springer Verlag. Heidelberg. 2003. pp. 37-69. [ Links ]
13. S. Sivanandam, S. Deepa. Introduction to Genetic Algorithms. Springer Verlag. Heidelberg. 2003. pp. 19-78. [ Links ]
14. P. Anderson. Analysis of faulted power systems. Ed. The Iowa State University Press. NewYork. 1995. pp. 56-127. [ Links ]
15. J. Mora. "Localización de Fallas en Sistemas de Distribución de Energía Eléctrica usando Métodos Basados en el Modelo y Métodos Basados en el Conocimiento". Tesis Doctoral. University of Girona. España. 2006. pp. 81-86. [ Links ]
16. IEEE Distribution System Analysis Subcommittee. Radial Test Feeders. IEEE Standards Board. (http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders.html). 1993. Consultada el 08 de mayo de 2009. [ Links ]
17. J. Dagenhart. "The 40-Ground-Fault Phenomenon". IEEE Transactions on Industry Applications. Vol. 36. 2000. pp. 30-32. [ Links ]
(Recibido el 03 de Junio de 2009. Aceptado el el 25 de febrero de 2010)
*Autor de correspondencia: teléfono: + 57 + 6 + 321 58 82, correo electrónico: jjmora@utp.edu.co (J. Mora-Flórez)