Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.56 Medellín Oct./Dec. 2010
Optimización de parámetros en los métodos Scan generalizados
Parameter optimization in general Scan methods
Laureano Rodríguez Corvea1*, Gladys Casas Cardoso2, Pavel Silveira Díaz3, Félix Arley Díaz Rosell3, Ricardo Grau Abalo2
1Departamento de Informática, Facultad de Ciencias Médicas de Sancti Spiritus, Olivos III, Circunvalación Norte, Sancti Spiritus, Cuba
2Laboratorio de Bioinformática, Centro de Estudios de Informática, Facultad de Matemática, Física y Computación, Universidad Central "Marta Abreu" de Las Villas, Cuba
3Departamento de Matemática, Facultad de Matemática, Física y Computación, Universidad Central "Marta Abreu" de Las Villas, Cuba
Resumen
El presente trabajo muestra una aplicación del diseño experimental al análisis de los parámetros de las técnicas Scan Lineal de detección de conglomerados, en su variante clásica y borrosa. Se utiliza un diseño experimental no paramétrico. El objetivo fundamental es estudiar la posible influencia de los valores de los parámetros: ancho de la ventana móvil y paso del Scan en ambas variantes del método, para obtener valores óptimos o cercanos a los óptimos.
Palabras clave:Método Scan, lógica difusa, diseño experimental no paramétrico.
Abstract
The present work shows an application of Experimental Design to the methods for disease cluster detection: Classic Scan and Fuzzy Scan. A non parametric experimental design for two factors is used. The fundamental target is to study the influence of the values of the parameters: the length width and the Scan step in order to determine optimum values.
Keywords:Scan method, fuzzy logic, non parametric experimental design.
Introducción
El desarrollo y la aplicación a problemas médicos de técnicas de detección de conglomerados, han crecido exponencialmente en las últimas décadas, [1-3]. Procedimientos con propósitos específicos como los métodos Scan [4-9], constituyen buenos ejemplos de ello. Estos métodos se han continuado desarrollando y se han reportado en la literatura varias generalizaciones [10-12]. Además, su campo de aplicación ha pasado de la medicina, a problemas de ingeniería, [13] pasando por nuevos campos como la Bioinformática [10]
El proyecto del genoma humano ha identificado miles de genes presentes en el núcleo de las células humanas y ha establecido la localización que ocupan estos genes en los 23 pares de cromosomas del núcleo. Los datos obtenidos a partir de la secuenciación del genoma humano pueden ayudar a relacionar las enfermedades hereditarias con genes concretos situados en lugares precisos de los cromosomas. Estas investigaciones proporcionan un conocimiento sin precedentes de la organización esencial de los genes y de los cromosomas. Muchos científicos creen que la identificación de la dotación genética humana revolucionará el tratamiento y prevención de numerosas enfermedades humanas [12], ya que penetrará en los procesos bioquímicos básicos que las sustentan.
Para ayudar a los investigadores a determinar el sentido de este aluvión de datos, se utilizan cada vez más instrumentos informáticos, como sistemas de información y gestión de bases de datos e interfaces gráficas de usuario, sistemas estadísticos y algoritmos inteligentes entre muchos otros [13].
Por otra parte, la teoría de la lógica borrosa ha constituido toda una revolución en el campo de las matemáticas [14]. Se han formalizado nuevas disciplinas como la teoría de control borroso, las probabilidades y la estadística borrosa, la optimización borrosa, por sólo mencionar algunas. El cúmulo de aplicaciones también ha crecido de manera notable en los últimos años y sigue en ascenso. La bioinformática no constituye una excepción.
Este trabajo se ubica en la intersección de todas estas áreas. Su objetivo fundamental es realizar un estudio de simulación en las diferentes variantes de los métodos Scan Generalizado [15], para analizar la influencia de los parámetros en su capacidad de respuesta. En investigaciones anteriores se ha probado la superioridad del Scan generalizado borroso sobre el clásico [16-18], pero una mala elección de los parámetros puede conllevar a respuestas erróneas en ambas técnicas. Es por ello que el investigador debe conocer las ventajas y las limitaciones de los métodos que usa, a fin de no arribar a falsas conclusiones.
Experimentación
A continuación se presenta el método Scan Generalizado, luego el método Scan Borroso y por último el diseño del experimento realizado.
El método Scan generalizado
Para lograr la generalización del método Scan, se realiza una transformación al método clásico, [15]. En vez de trabajar sobre datos tipo fecha como inicialmente fue concebido, la técnica Scan trabaja con una cadena binaria, donde el valor uno representa la categoría que interesa, y el valor cero representa todo lo demás. El método tratará de determinar si existen conglomerados de unos dentro de la cadena binaria que se le presenta [15, 19-21].
El método Scan generalizado es similar al Scan clásico; se fija un tamaño de ventana la cual se mueve sobre la cadena binaria con un paso determinado, se calcula el número máximo de uno de cada una de las ventanas formadas (w), siendo éste el estadígrafo del método y el cálculo de la significación se realiza utilizando la fórmula aproximada de Naus, ver ecuación (1) [7].

Para el Scan Lineal Generalizado Q* puede aproximarse para cualquier L>2 a partir de sus valores con L=2 y L=3, ver ecuación (2).

Para el Scan Circular Generalizado Q* puede aproximarse para cualquier L>2 a partir de sus valores con L=2, L=3 y L=4, como se muestra en la ecuación (3).

En [15] se encuentra la generalización del método Scan en sus dos variantes Lineal y Circular. Los resultados del método Scan dependen de dos parámetros: el ancho de la ventana móvil y el paso con el que avanza dicha ventana. De forma general resulta muy difícil determinar cuáles son los valores apropiados para estos parámetros. Si el problema que se quiere resolver es por ejemplo de diagnóstico médico quizás no sea tan complicada la elección de estos valores, pues existe personal médico altamente calificado y especializado en el conocimiento de determinadas afecciones que pueden brindar con bastante precisión ideas acertadas acerca de los valores posibles a utilizar.
Si por el contrario nos enfrentamos a situaciones más complicadas, o a problemas de los que se tenga menos conocimiento previo, sí será muy difícil la elección adecuada de los valores de los parámetros. Un ejemplo de tal situación lo constituyen los problemas de bioinformática.
En un experimento con datos simulados [20], se demuestra que los resultados de los métodos Scan dependen muy fuertemente de los valores de sus parámetros: ancho de la ventan móvil y paso del movimiento. Para mejorar estos resultados, se aplican algunos elementos de la teoría de la Lógica Borrosa. Surge así el método Scan borroso.
El método Scan borroso
El método de Scan Borroso en sus variantes Lineal y Circular considera la ventana móvil como una ventana borrosa en la que se suavizan sus bordes con alguna función de pertenencia. Ese hecho trae modificaciones importantes con respecto al método original, pues el estadístico de Naus: cantidad máxima de casos en una ventana (w), es ahora un valor real y no entero como antes.
Para suavizar los bordes de la ventana móvil sobre una secuencia binaria, se introducen términos adicionales en sus extremos. A la cantidad de términos adicionales en uno de los extremos se le denominará grado de suavizamiento empleado [16-18]. Los valores de la ventana móvil de tamaño k: se calculan como se explica en la ecuación (4):

Donde:
t = tamaño de la ventana móvil
g = grado de suavizamiento
Scan Lineal
Secuencia analizada:
S1, S2, S3,
.Sn
i <1 entonces Si = 0
i >n entonces Si= 0
Scan Circular:
Secuencia analizada:
S1, S2, S3, . . . . . . . . . . . . , Sn, Sn+1, Sn+2, . . . . , S n + t-1.
Donde Sn + i = Si para i = 1, 2, . . . . t-1
i <1 entonces S i = S n-1
i > n+t-1 entonces Si = S i-n
La concepción utilizada por Naus [7], para el cálculo de la significación del test, necesitan ser modificadas porque se basan en distribuciones de Poisson y esta se define sólo para variables discretas.
Para ello se utilizaron las siguientes variantes, que aparecen explicadas en [17, 18]:
1. El valor real obtenido en el estadígrafo se aproxima al entero más próximo. Las funciones de probabilidad y de distribución de Poisson se utilizan repetidas veces en el cálculo de la significación según Naus, luego el error que se comete con la aproximación pudiera propagarse de manera significativa [17, 18].
2. Utilizar una aproximación basada en las distribuciones de Poisson y Uniforme. Esta forma de calcular la significación utiliza una distribución de Poisson hasta la parte entera del estadístico. La parte fraccionaria se aproxima utilizando una distribución continua uniforme.
Sea k.f el estadígrafo real (k parte entera y f parte fraccionaria) y 1 como parámetro de la distribución de Poisson, entonces la función de densidad de la distribución uniforme se define como se explica en (5):

Para calcular las fórmulas de Naus es necesario introducir leves transformaciones en el cálculo de las mismas. Estos cambios aparecen explicados en detalles en [17].
3. Para calcular la significación del estadígrafo real se usan dos funciones de interpolación de grado cuatro. Con los valores enteros alrededor del estadígrafo se obtienen las dos funciones de interpolación: una relacionada con la probabilidad de Poisson y la otra con su distribución acumulativa. De esta forma se calculan aproximadamente el valor de la probabilidad y de la distribución acumulada necesarias en la fórmulas de Naus, las cuales deben ajustarse para que puedan utilizar las nuevas funciones [17, 18].
El resultado obtenido está particionado en dos subconjuntos borrosos identificados por las etiquetas: "no significativo" y "significativo". Cada una de estas particiones le corresponde una función de inclusión o pertenencia tipo S, ver figura 1.
Estas particiones toman valores en el intervalo [0,1], son particiones completas y no hay solapamiento entre ella ver figura 1. Por lo explicado se usa un desborrosificador por máximo [22], es decir el método da como resultado final a la partición que alcanza mayor valor al evaluarla en sus funciones de membresía.
Diseño del experimento
Si se conocen cuáles efectos producen sobre la respuesta los parámetros: paso del Scan y tamaño de la ventana móvil, y su interacción, se podrán orientar valores adecuados de estos parámetros para optimizar el método Scan. Esto puede lograrse con un experimento factorial que permite estudiar simultáneamente varios factores y sus interacciones, de modo que los tratamientos se forman por todas las posibles combinaciones de los niveles de los factores [23].
Los parámetros no siguen una distribución normal y es conocido que, en las versiones de paquetes estadísticos como el SPSS (Statistical Package for the Social Science), no están implementadas las posibilidades de hacer análisis de varianza multifactorial no paramétricos. Las alternativas clásicas para resolver problemas de este tipo se basan en el uso de Técnicas de Análisis de Datos Cualitativos (Categóricos). Si en particular la variable dependiente puede ser dicotomizada, o discretizada en categorías nominales, puede utilizarse la Regresión Logística Binaria o Multinomial que permite detectar efectos de factores principales o de interacciones. Cuando todas las variables predictivas son categóricas, se puede pensar en el uso de procedimientos Loglinear o Probit del SPSS.
En los trabajos [16-18] se demuestra la superioridad del Scan Borroso sobre el Scan Generalizado por lo que se necesita un análisis de varianza con apenas dos factores en un diseño equilibrado y las alternativas anteriormente mencionadas no producen resultados suficientemente buenos, por lo que se necesita hacer un análisis de varianza no paramétrico bifactorial, capaz de detectar la posible influencia de cada uno de los dos factores principales así como su interacción
Análisis bifactorial no paramétrico
Existe un fundamento teórico de cómo puede realizarse un tal análisis en el caso de diseños equilibrados. La idea esencial fundamentada por R. R. Sokal and F. J. Rohlf, 1995 [24] fue elaborar un Análisis de Varianza Bifactorial No Paramétrico ranqueando la variable dependiente, como lo hace el test de Kruskal-Wallis. Se utilizan las sumas de cuadrados de la variable dependiente ranqueada y se recalculan los grados de libertad de cada factor y su interacción para ofrecer finalmente una significación de cada efecto. Si algún factor tiene más de dos niveles, se pueden utilizar tests de comparaciones múltiples clásicos que se basan fundamentalmente en rangos para obtener subconjuntos homogéneos, por ejemplo, el test de Dunnet C, válido incluso ante falta de homogeneidad de varianzas.
Algoritmo para un análisis bifactorial no paramétrico.
1. Ranquear la variable dependiente.
2. Aplicar el Análisis de Varianza sobre la variable dependiente ranqueada, para obtener la suma de cuadrados (SC) por cada factor y su interacción, así como sus grados de libertad.
3. Calcular el CMT (Cuadrado Medio Total)
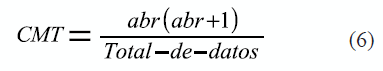
Donde,
a: es el número de niveles del primer factor b: es el número de niveles del segundo factor
r: es el número de réplicas de cada combinación
4. Calcular el estadígrafo H para cada factor y la interacción

5. Calcular la significación de cada H utilizando la distribución de Chi-cuadrado, teniendo presente los grados de libertad del factor o de la interacción analizada. (La variable H tiene distribución Chi-cuadrado).
Para facilitar el trabajo con el algoritmo anterior se han programado tres funciones simples en el paquete Mathematica 6,0 una de ellas utiliza el contexto de ANOVA dentro del paquete de Análisis de Varianza, para realizar el análisis paramétrico a la variable ranqueada.
A continuación se muestra la implementación de las cláusulas fundamentales del ANOVA bifactorial no-paramétrico en el paquete Matemática:

La función RankValues tiene el parámetro:
values: lista de valores de la variable dependiente que serán ranqueados.
La función test tiene los siguientes parámetros:
nrep: Representa el número de réplicas (constante en cada combinación de valores de los factores)
lfl: Niveles del factor 1
lf2: Niveles del factor 2
namef1: Nombre del factor 1
namef2: Nombre del factor 2
sqsumf1: Suma de cuadrados del factor 1
sqsumf2: Suma de cuadrados del factor 2
sqsumf1f2: Suma de cuadrados de la interacción
La función BifactorialNonParamANOVA tiene los siguientes parámetros:
nrep, lf1, lf2, namef1, namef2: Como en la función test
data: Conjunto de datos de la forma mostrada en 1 del Resumen Práctico
Una vez cargadas las funciones 1, será invocada la función BifactorialNonParamANOVA con los parámetros correspondientes a cada análisis. En nuestro ejemplo, sería así:
BifactorialNonParamANOVA [{ { 1,1,100.}, { 1,2,100.},{ 2,1,100.},{ 2,2,100.},{ 3,1,86.}, { 3,2,84.85},{ 1,1,100.},{ 1,2,99.3},{ 2,1,100.}, { 2,2,100.},{ 3,1,81.65},{ 3,2,78.95},{ 1,1,99.15}, { 1,2,87.1},{ 2,1,99.9},{ 2,2,96.25}, { 3,1,74.1},{ 3,2,68.2}},3,3,2,"Ventana","Paso"] La respuesta del Mathematica será como la siguiente:

Generación de secuencias
Para probar el experimento se generaron verdaderos y falsos conglomerados utilizando secuencias aleatoria de ceros y unos, generados según una distribución de Bernoulli. Se definen diferentes tamaños para el largo de la secuencia: n = 10.000, 100.000 y 1 000.000 [20]
Para generar verdaderos conglomerados se siguen los siguientes pasos:
-Un quinto de la población se genera con una probabilidad grande de presencia de unos (categoría de interés). Esta probabilidad la puede manejar el usuario.
-El resto de la población es generada con una probabilidad pequeña de presencia de unos (categoría de interés).
- En el conjunto de menor probabilidad de unos se determina una posición aleatoria y se inserta en ella el conjunto de mayor cantidad de unos. De esta forma se obtiene una secuencia de ceros y unos que tiene al menos un conglomerado.
Para generar falsos conglomerados se genera la población con una probabilidad de 0,2 de presencia de unos (categoría de interés).
Se generan conjuntos de verdaderos y falsos conglomerados de 1000 elementos cada uno en las secuencias de tamaño anteriormente descrita.
Resultados y discusión
Dada un tamaño de ventana móvil y un paso, el método Scan clasifica si en una secuencia existe al menos un conglomerado de la categoría de interés o no, por lo que nos interesa es medir la influencia que producen dichos parámetros en su desempeño. Por tal razón la información analizada es la exactitud obtenida utilizando el conjunto de verdaderos y falsos conglomerados de cada una de las poblaciones. Con el objetivo de generalizar los resultados en las distintas poblaciones el tamaño de la ventana se trabajan en porcentaje con relación al tamaño de la secuencia.
Se conoce que en el Método Scan las curvas de desempeño del clasificador con respecto al parámetro ventana tiene un comportamiento cuadrático fundamentalmente para la primera mitad de la secuencia, para la segunda mitad el desempeño es pequeño y va decreciendo hasta ser nulo a medida que la ventana se acerca al final de la secuencia [20]. Para el análisis de los resultados se fija el tamaño de la ventana alrededor de los niveles: 6%, 25% y 50%.
Se realizan varios experimentos con los factores ventana y paso, con el objetivo de verificar como influyen los factores en cada experimento por separado. El factor paso influye en el valor de comienzo del factor ventana móvil, por lo que los niveles de los factores de cada experimento son detallamos en la tabla 1.
Como se ha demostrado el parámetro suavizado puede influir en los resultados, por lo que es controlado en experimentos para suavizado 0 (Scan Clásico Generalizado) y suavizado 4 (Scan Borroso). Cada experimentos tienen tres replica cada una con probabilidades diferentes de presencia de la categoría de interés en el conglomerado (probabilidad de 0,9, 0,7 y 0,5)
En las figuras 2 y 3 se ilustra que el método Scan Lineal y el método Scan Circular en sus variantes clásica y borrosa, tienen un comportamiento similar en su desempeño en todas las secuencias teniendo en cuenta que:
-El factor ventana móvil aumenta su respuesta al cambiar sus valores del 6 % al 25 % y disminuye su respuesta al variar sus valores del 25% al 50 % en todos los experimentos.
-El factor paso en el primer experimento (paso con niveles iguales a 1 y 2 respectivamente) tiende a mantener la respuesta al variar de un nivel al otro, en los experimentos restante este factor disminuye la respuesta de significación al pasar del nivel bajo al alto. A medida que el paso aumenta la respuesta disminuye más rápidamente.
En el Scan Lineal y Scan Circular para cada población la variante suavizada obtiene mejores resultados que la variante clásica, observe como para todos los niveles del factor ventana la variante borrosa obtiene mejores resultados que la variante clásica, destacándose que el nivel inferior de la ventana en la variante suavizada es la que obtiene un notable aumento de los resultados comparados con los restantes niveles, estos resultados concuerdan con los planteados en [16-18]
En la tabla 2 se presenta la significación de los factores ventana, paso y la interacción de ellos en cada uno de los experimentos de las diferentes poblaciones, se concluye que el total de casos bien clasificados es afectado en todos sus experimentos significativamente por el factor ventana con una confiabilidad de 90%. Mientras que el factor paso solo afecta el tercer experimento (paso con niveles iguales a 1 y 25 respectivamente) de todas las poblaciones significativamente con una confiabilidad de 90%; por lo que se corrobora que a medida que el paso crece afecta desfavorablemente el desempeño del clasificador. La interacción no afecta significativamente a ningún experimento.
Ejemplo en bioinformática
La Epilepsia Progresiva Miclónica de tipo Unverricht-Lundborg (EPM1) es una enfermedad congénita autosómica recesiva. La causa de esta enfermedad es una mutación en el gen (CSTB) que codifica un inhibidor de la cistein proteasa, la cual consiste en la repetición anormal (35-70 veces) del dodecámero (CCCCGCCCCGCG) que se encuentra repetido de dos a tres veces en la región 5' del gen en los individuos sanos [25]
El gen Cystatin B (CSTB) mapeado en locus 21q23.3, se expresa mediante una secuencia binaria de la siguiente forma: los dodecámeros de interés (CCCCGCCCCGCG) se representan por unos y el resto de los dodecámeros por ceros. Posteriormente, a esta secuencia binaria se le aplica el método Scan Lineal Generalizado en sus variantes clásica y borrosa con suavizado tres, además los parámetros "ventana móvil" y "paso" pueden tomar diferentes valores.
Observe en la tabla 3 cuando el parámetro "paso" es igual a uno con cualquier valor de la "ventana móvil", para los pacientes sanos no se obtiene significación. Sin embargo para los pacientes enfermos se obtiene significación en todos los casos de ambas variantes, excepto para la variante clásica que no detecta enfermos en las ventanas móviles pequeñas, es decir clasifica a un enfermo como sano, no aconsejable en el campo médico. Esto demuestra la superioridad del método borroso.
Cuando el valor del parámetro "paso" es igual a cinco la "ventana móvil" se mueve más rápido, lo que implica menor complejidad algorítmica, pero tiene el inconveniente de que se pierden datos al moverse la ventana, por esa razón los resultados son menos confiables que cuando el valor del "paso" es uno. Obsérvese que existen diferencias en los valores de las probabilidades lo que no afectan los resultados finales, excepto para "ventanas móviles" pequeñas, por ejemplo, cuando el "paso" toma valor seis se detecta al sano (CCCCGCCCCGCG)3 como enfermo.
Conclusiones
Las variantes clásica y borrosa de los métodos de Scan Lineal y Circular se caracteriza por:
-Afectar las respuestas al variar el tamaño de la ventana.
-Respuestas pobre o nula para valores grande del factor ventana.
-Mejores resultados para ventanas de tamaños cercanos al 25 % de la población
-La variante borrosa aumenta considerablemente su respuesta para valores pequeño del factor ventana con respecto a la variante clásica.
-Los métodos tienden a mantener respuestas similares para valores pequeños del factor paso, pero a medida que el paso aumenta disminuye la respuesta de los métodos, siendo estas diferencias significativas cuando el paso es grande.
- Los métodos en una misma secuencia obtienen mejores respuesta en su variante borrosa que la clásica con respecto al factor ventana o paso. [20]
Referencias
1. G. Jacquez, L. W aller, R. Grimson, D. Watenberg. "A k-nearest neighbor test for space-time interaction". Stat. in Med. Vol. 15. 1996. pp. 1934-49. [ Links ]
2. M. D. Joner, W. H. Woodall, M. R. Reynolds. "Detecting a rate increase using a Bernoulli scan statistic". Statistics in medicine. Vol. 27. 2008. pp. 2555-2575 [ Links ]
3. R. Marshall. "A review of methods for the statistical analysis of spatial patterns of disease". J. of the Royal Stat.l Soc. Assoc. Vol. 154. 1991. pp. 421-441. [ Links ]
4. J. Glaz. "Aproximations for the tail probabilities and moments of the Scan statistics". Statistics in medicine. Vol. 12. 1993. pp. 1845-1852. [ Links ]
5. J. Glaz, N. Balakrishnan. "Scan Statistics and Applications". Birkauser. Statistics for Industry and Technology. Ed. Hardcover. Boston. 1999. pp. 269- 284. [ Links ]
6. J. Glaz, J. Naus, S. Wallenstein. Scan Statistics. Ed. Springer Verlag. 2001. pp. 81-96.7. [ Links ]
7. J. I. Naus. "Approximations for distributions of Scan statistics". Journal of the American Statistical Association. Vol. 77. 1982. pp. 177-183. [ Links ]
8. M. Kulldorff, F. Mostashari, L. Duczmal, K. Yih, K. Kleinman, R. Platt. "Multivariate scan statistics for disease surveillance". Statistics in Medicine. Vol. 26. 2007. pp. 1824-1833. [ Links ]
9. C. E. Priebe, J. M. Conroy, D. J. Marchette, Y. Park. "Scan Statistics on Enron Graphs". Computational & Mathematical Organization Theory. Vol. 11. 2005. pp. 229-247. [ Links ]
10. C. Langrand. "Scan Statistics: definición y ejemplos". Seminario ANY 2005. Ed. Université Sciences et Technologies de Lille (Lille-1). Universidad Politécnica de Cataluya. España. 2005. pp. 1-11. [ Links ]
11. A. W. Martin. "A Generalised Scan Statistic Test for the Detection of Clusters". International Journal of Epidemiology. Vol. 10. 1981. pp. 289-293. [ Links ]
12. R. Nussbaum, L. Peltonen. "Genetics of disease: Recent advances in the genetics of human disease offer something new for every scientific interest ". Current Opinion in Genetics & Development. Vol. 17. 2007. pp. 163-165. [ Links ]
13. P. Baldi, S. Brunak. Bioinformatics: the machine learning approach. 2 ed. Ed. MIT Press. New York. 2001. pp. 47-241. [ Links ]
14. L. A. Zadeh. "Nacimiento y evolución de la Lógica Borrosa, el soft computing y la computación con palabras: un punto de vista personal". Psicothema. Vol. 8. 1999. pp. 421-429. [ Links ]
15. L. Rodríguez, G. Casas, R. Grau, M. Pupo. "Generalización de dos métodos de detección de conglomerados. Aplicaciones en Bioinformática". Revista de Matemática: Teoría y Aplicaciones. Vol. 15 2008. pp. 27 - 40. [ Links ]
16. L. Rodríguez, G. Casas, R. Grau. "Linear Fuzzy Scan Method to Detect Clusters. A Bioinformatic Application". XIV Latin Ibero-American Congress on Operations Research (CLAIO 2008).Ed. Cartagena de Indias. Colombia. 2008. pp. 536-540. [ Links ]
17. L. Rodríguez, G. Casas, R. Grau, O. Gómez. "Approximations for the distribution of Fuzzy Scan Statistics". Investigación Operacional. Vol. 30. 2009. pp. 131-139. [ Links ]
18. L. Rodríguez, G. Casas, R. Grau, Y. Martínez. "Fuzzy Scan Method to Detect Clusters". International Journal of Biomedical Sciences. Vol. 3. 2008. pp. 111-115. [ Links ]
19. L. Rodríguez, G. Casas, R. Grau. "Aplicación de los métodos Scan en Bioinformática". Uciencia 2006. II Conferencia Científica. Ed. UCI. La Habana. 2006. pp. 13-18. [ Links ]
20. L. Rodríguez, G. Casas, R. Grau. "Validación del método Scan Generalizado con verdaderos falsos conglomerados". X Congreso Nacional de Matemática y Computación. Ed. Holguín. Holguín (Cuba). 2007. pp. 21-24. [ Links ]
21. L. Rodríguez, G. Casas, R. Grau, G. Cardoso, S. Ortega, M. Pupo. "Scan Statistics. Bioinformatics Applications". First International Workshop on Bioinformatics Cuba-Flanders. Ed. UCLV. Santa Clara (Cuba). 2006. pp. 33-39. [ Links ]
22. B. Martín del Brío, A. Sánchez. Redes Neuronales y Sistemas Difusos. 2a ed. Ed. Alfaomega. México. 2005. pp. 241-341. [ Links ]
23. D. C. Montgomery. Diseño y Análisis de Experimentos. Ed. Limusa. México. 2008. pp. 686. [ Links ]
24. R. R. Sokal, F. J. Rohlf. "The principles and practice of statistics in biological research". Biometry. 3a ed. Ed. W. H. Freeman and Company. New York. 1995. pp. 123-234. [ Links ]
25. K. Alakurtti, E. Weber, R. Rinne, G. Theil, D. Lindhout, P. Salmikangas, P. Saukko, U. Lahtinen. "Loss of lysosomal association of cystatin B proteins representing progressive myoclonus epilepsy, EPM1, mutations". Hum Genet.Vol. 13. 2005. pp. 208-215. [ Links ]
(Recibido el 9 de Agosto de 2008. Aceptado el 31 de agosto de 2010)
*Autor de correspondencia: teléfono: + 53 + 422 815 15, fax: + 53 + 422 816 08, correo electrónico: corvea@uclv.edu.cu. (L. Rodríguez Corvea)