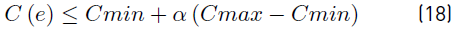1. Introduction
Today, we are surrounded by Electrical and Electronic Equipment (EEE) that make it easier to perform daily tasks, these are made up of a combination of parts and elements that operate with electricity and perform several jobs and certain functions. When the owner considers that their useful life is over, they are discarded and they turn into Waste Electrical and Electronic Equipment (WEEE).
In 2013, the law 1672 in Colombia was created, and later in 2017, the National Policy for the Integrated Management of WEEE was approved. Those agreements give differentiated and comprehensive treatment to wastes and set a goal to have in year 2032 a system for collecting WEEE for 90% of types of electrical and electronic equipment as a solution to the approximately 275,000 tons of electronic waste produced annually [1].
This research seeks to develop a WEEE collection optimization model, which can be modeled as a localization and routing problem, divided into two phases. In the first phase, the aim is to locate stationary points in the communes, so that users can access them easily and quickly to deposit the corresponding waste in special containers. In addition, and as a novelty in this phase to each located point different devices for the collection are assigned.
In the second phase, the corresponding collection routes are designed through the established points, with the objective criteria of minimizing transportation costs. And, a GRASP algorithm is implemented to obtain good solutions that allow the creation of a WEEE collection network.
Through of the world, the generation of WEEE has become a problem of increasingly alarming proportions. According to [2], "WEEE is one of the fastest-growing streams due to its short product life cycles (PLCs) and the rapid changes in consumer preferences regarding its availability".
The present work seeks to design a WEEE collection network for the city of Bucaramanga, analyzing communes 6, 7 and 8 of this city as a case study, taking into account current regulations regarding the collection of electronic waste, with the aim of optimizing the costs associated with the implementation of the system.
For this project, it is planned to collect only WEEE categories 3, 5 and 6 according to European Union directives, corresponding to batteries, lamps and EEE with dimensions less than 50 cm.
Our research is an initial work for a big project that the City of Bucaramanga is planning, because in the future, the idea is to replicate this work in all 16 communes of city. Thus, if we think about the complex future model, working with a metaheuristic technique such as GRASP over an exact technique is considered a widely reasonable idea.
2. Literature review
In the literature, the problem has been studied from various approaches. Various authors such as [3] state that the success of an efficient WEEE collection model depends, to a large extent, on the user's perception of the value of the electrical or electronic equipment (EEE). When an EEE has lost value for the user and it decides to throw EEE away, frequently is not found a disposal site or program for the device and ends up disposing that with conventional garbage, which aggravates the contamination problem [4].
For this reason, mathematical optimization models have been created in the literature, such as one developed by [5] in which they developed a mixed integer programming model that sought to optimize the structure of the collection network by minimizing the costs of collection, with transportation costs, daily operation costs and storage costs of electrical and electronic waste.
Since 2005, many authors such as [6] have worked on this topic like supply chain reverse design for WEEE collection. In 2018, several authors, such as [7], were working on this topic in the same way, incorporating additional elements to modeling.
Many authors such as [8] have focused their work on the allocation and location of pickup points. In the same way, [9] worked a case study in Denmark where they integrated optimal location of municipal points with manufactures enterprises. And, [10] developed a stochastic model that evaluated the best location of collection and storage points with possibility of interchange among them.
Other authors such as [11] have worked on the design of collection routes between waste collection points. They presented a model for optimizing the WEEE transport network, and they considered vehicle capacity and the fuel consumption costs associated, with objective criteria to minimize costs and carbon dioxide emissions. For the solution of optimization models applied to real contexts, the use of metaheuristics like the genetic algorithms is the most frequent in the literature. For example, [12] designed a genetic algorithm to solve the optimization WEEE collection network in Opole, Poland. Another outstanding work is the one carried out by Mar-Ortiz [13] in which the authors worked a model of routing of vehicles with time windows for a case of WEEE.
3. Location of collection points and allocation of containers problem
In order to find the best collection points, a model based on the facility location problem (FLP) is proposed, widely studied in the literature. A mixed integer linear programming model is formulated with the objective criteria to minimize the costs associated with the installation of containers and the distance to be traveled by users from their homes to the assigned collection point. The potential points are made up of a series of public interest points such as schools, community action boards, immediate action centers (IACs) and shopping centers, the latter under the extended responsibility status of the producer and marketer, must offer users the means to dispose of WEEE.
The mathematical model, in addition to determining the collection points, assigns the demand generation centers and determines the number of containers, of each type, to be installed at each point, complying with a series of restrictions. The mathematical model developed is described below:
Indexes
i = WEEE generation points i (1, 2..., n)
j = location points j (1, 2, ..., m)
t = Type of WEEE t (1, 2, 3)
Variables
B tj = Number of containers type t ubicated in the spot j
Parameters
M = Maximum cost of going from a generation point to a location point.
U = Large integer number.
Dti = Demand of WEEE type t generated in point i.
Pt = Cost of container t.
Capt = Capacity in Kg of the container assigned for WEEE type t.
Cosij = Cost of going from generation point i to location point j.
Cp = Point opening cost.
Objective function
Restrictions
Equation (1) represents the objective function that minimizes the costs associated with the distance traveled by the user, the opening costs of the point and the cost of the containers to be installed. Restriction (2) causes points Y1, Y2, and Y3 to be opened and assigned users and containers (This points have to be opened because in the real case studied in this paper, these points are created and used for collection several years ago), restriction (3) ensures that all WEEE generation points must be served by a location point, restriction (4) indicates that the associated cost for the distance travelled from a generation point to the assigned location point does not exceed the established limit, restriction (5) indicates that a location point will only be opened if there is a waste demand associated with that location, restriction (6) defines that containers must be assigned if the point is opened. In the last restrictions [(5) and (6)] U as Large integer number, which gives a possibility to activate the binary variables.
The restriction (7) refers to the capacity of the containers installed at each point shall be greater than the associated demand for each type of WEEE allocated to it. Finally, restriction (8) indicates the binary character of variables X, Y, while restriction (9) indicates the integer positive nature of variable B.
3.1 Computational results for location of collection points and allocation of containers problem
The entire mixed linear programming model was programmed in the GAMS optimization software. Initially there were 26 potential collection points and the algorithm selected 12 points of them. And the same time, the algorithm assigned users and containers to them according to the established restrictions. Table 1 lists the selected points.
4. Routes collection problem
In order to comply with the planning horizon of the 4 fortnightly routes project, the segmentation of the target territory is carried out. After that, the CVRP model proposed and our GRASP algorithm are explained.
4.1 Territory segmentation
There are several methods of segmentation, which could be hierarchical, partitioner or density, which vary according with group zones. The partitioning algorithm K-means, proposed by James MacQueen in 1967, which consists of 3 main steps [14], is used to perform the segmentation of the territory under study:
Initialization phase: K-means places k points in the space where the vertices meet. The determined points represent the initial centroids of the groups.
Assignment phase: at this stage the algorithm assigns each vertex to the group with the nearest centroid. To do this, the distance between the vertex and each centroid is measured. The most commonly used distances is Euclidean, but in this paper distances obtained by Google Maps are used.
Update phase: after all the vertices have been assigned to each initial centroid, its location changes, therefore, the algorithm recalculates the position of the k centroids.
The proposed algorithm is programmed in Matlab version R2018a through the function [idx, C] = kmeans (X,k) with the use of non-Euclidean distances, it is computed by the Google Maps API, from which a system of coordinates (x, y) with origin (x=0, y=0) is designed in the Metropolitan Clean Point and the distances in meters corresponding to the defined axes are found. Different comparisons and adjustments are made to choose the best segmentation of the case study area.
4.2 Routing modelling
The CVRP is one of the most studied extensions of the vehicle routing problem in the literature, whose objective is to design routes that visit all customers minimizing the associated costs without exceeding the capacity of the vehicles. For the present research work, the mathematical model for the collection of WEEE in Galicia, Spain proposed by [15] is taken as a base, because this work developed a GRASP algorithm for a VRP problem similar to ours. The transport network is represented by a graph G = (V, A), where V= {0,1, 2, 3..., n} expresses the set of vertices or nodes and A = {(i, j); i, j ∈ V} refers to the set of arcs through which the vehicles will make their journeys taking into account that i≠ j. This graph is directed with asymmetric distances between each node i and j.
The vertices 0 and n+1 represent the initial and final node corresponding to the Clean Point from where the vehicles will depart and where they will later finish their journey, therefore, no arc can begin at vertex n+1 nor end at vertex 0. The rest of the vertices represent the points located with the location model as well as the fixed points corresponding to the residential complexes to which containers are assigned according to their demand. We have a fleet of K vehicles with limited capacity C.
Each vertex should be visited only by one vehicle per route, considering that the demand of each point must be less than the capacity of the vehicle.
The mathematical formulation of the CVRP is presented below:
Parameters
K = Number of vehicles of equal capacity.
C = Vehicle capacity.
Dit = Quantity of WEEE t in kilograms generated at node i.
Cosij= Cost per distance to go from node i to node j.
Variables
Objective function
Restrictions
The target function (10) is the sum of the associated costs with the total distance travelled between all nodes. Restriction (11) indicates that each collection point must be served by a single vehicle, where j ϵ Δ + (i) represents the complete networks starting from node i and ending in node j. The restriction (12) ensures that each vehicle can only reach one collection point j from the starting point and the restriction (13) states that each route has only one point that reaches the depot, so these equations restrict the number of journeys the vehicle makes to one.
The restriction (14) states that the number of vehicles entering a node is the same as the number leaving, ensuring that each node is served only once. The restriction (15) indicates that the sum of the total amount of WEEE collected per route is less than the capacity of the vehicle. The restriction (16) is used for elimination of subtours. Finally, restriction (17) shows the binary nature of the variable X ijv .
4.3 GRASP Algorithm for CVRP solution
We used a GRASP algorithm combined with exchange operators and 2-opt to obtain the best possible solutions for our case study. GRASP is an iterative method, developed in the 1980’s, in which each iteration has two phases, a construction phase and a local search phase. In the first phase the aim is about to build feasible solutions, and in the second phase the goal is to find a minimum (or maximum depending on the optimization criterion) from the solution built [16]. The algorithm has the following phases for each iteration:
1. Construction Phase
1.1. Solution initiation phase, with evaluation of incremental costs C(e) and determination of Cmax and Cmin.
1.2. Building a RLC shortlist of candidates
1.3. Random selection of the elements of the RLC to fill the feasible routes
2. Local search phase
2.1. Application of exchange operator 1-1 and operator 2-opt to improve the solution
2.3. Comparison of the solutions obtained
2.4. Updating the best solutions
For the construction of the shortlist of candidates, the algorithm calculates (Equation (18)] the maximum and minimum incremental costs of the input matrix and finds the value of the evaluation Greedy function:
The degree of randomness of the Greedy function is controlled by the parameter α, which after the application of tests with several instances is adjusted to the value of 0.1. Values that are less than the Greedy function will enter the restricted candidates list (RCL), from which a node is randomly selected, inserted into the path and removed from the input matrix. The process is repeated until the capacity of the vehicle is occupied, at which point the route is closed by returning to the starting node and a new route is opened if there are still unassigned vertices. When all points have been assigned to a route, the construction phase ends.
In order to improve the solutions obtained in the construction phase, for the local search, the 1-1 inter-route exchange operator is implemented, which selects two nodes at random from two different routes and exchanges them verifying compliance with the restrictions. After each route, the 2-opt exchange operator is applied to improve the total cost of the routes obtained. The algorithm runs until the limit of the 100 established iterations is reached and returns the best routes obtained.
To analyze the performance of our proposed algorithm, we tested it with 15 literature instances proposed by [17]. And, we compared our results in the same table with solutions obtained for GRASP algorithm of [18] also with solutions obtained with DELS algorithm of [19] and CLOVES algorithm of [20]. The comparisons are shown in Table 2.
The results of our algorithm did not get a better solution than others, however, it offers good solutions for studied instances. Then we conclude that our algorithm is suitable to continue to the next step of our research.
4.4 Computational results of GRASP algorithm in our case study
To define the WEEE collection routes in the target zone, the GRASP algorithm with local search developed for each of the designed clusters is applied. The application of the algorithm requires as input data the matrix of costs by distance and the demands of the points for each grouping of nodes. There are 4 clusters that include the points obtained from the localization model plus the residential complexes defined as fixed points, to which a maximum of one vehicle is assigned. For the target area of the case study, it is proposed to launch two weekly routes to collect the estimated fortnightly demand. The Table 3 summarizes the results obtained for each cluster showing the total cost associated with the distance travelled and the amount of WEEE collected per route.
The solutions obtained using our proposed algorithm presents good results compared with other of literature, when in average only a 7.3% is the GAP with then.
5. Conclusions
The application of exact techniques and metaheuristic algorithms for the solution of combinatorial optimization problems applied in real contexts allows good solutions in an acceptable computational time.
In the present study, for allocation and location problems, we used a MILP and found an optimal solution using GAMS software. Our next step is to take in the future all of 16 communes of Bucaramanga and work with our model again.
Further for the routing problem, our segmentation technique of K-means obtaining good results.
The use of the GRASP algorithm with local search operators to solve the CVRP formulated in the case study made it possible to minimize the costs associated with the collection of WEEE at the selected collection points. And, our algorithm was tested with other references providing good solutions for studied instances.
Metaheuristics techniques for routing and other problems have been extensively studied in the literature and the current trend is the development of hybrid algorithms that combine one or more techniques, in order to provide high quality solutions to the different variants of VRP applied to real contexts.