1. Introduction
Controllers are a vital part of industrial processes, and plants around the world use predominantly proportional-integral-derivative (PID) controllers to keep important process variables at desired setpoints. It is estimated that over 90% of control loops employ PID control, quite often with the derivative gain set to zero, i.e., PI control[1]. Although academic research in control theory has developed tools for tuning controllers and measuring performance, only about 32% of control loops have acceptable performance, and 36% of the processes are operating in open-loop because of problems with the controller[2].
Tuning equations are a tool to adjust controller parameters, which, due to their versatility and generalization capabilities, provide a way to optimize the response of processes finding specific parameters according to performance requirements. For example, to preserve the integrity of actuators, some parameters can be found to minimize the variation of the controller output[3]. Tuning equations for a PID controller based on Internal Model Control (IMC), where the IAE is minimized for a second-order inverse response system with a time delay have been developed[4]. Also, tuning equations for PID controllers to be implemented in photobioreactors, by optimizing the IAE and variance for both controller output and process variables have been investigated[5]. For instance, tuning equations to optimize the process performance using PID controllers for heat exchangers and thermal processes have been used[6].
New tuning approaches for PID controllers include the use of genetic algorithms to obtain controller parameters[7], and metaheuristic algorithms like swarm optimization, which use as a performance index the IAE[8]. In other swarm intelligence algorithms, the estimated mathematical models of systems or processes can be used to modify the parameters of PID controllers. These adaptive control strategies can be implemented in commercial programmable logic controllers (PLC)[9, 10].
No doubt, control loops are the most critical components in automation systems. Energy and raw material consumption, operation safety, product quality, and thus, the financial profitability are directly or indirectly linked to the performance of process control systems[11]. Hence, a vital interest for any company must be to reach, restore, and maintain top performance of control loops. However, most of the process control systems currently used are complex, usually comprising many hierarchical levels; thus, it is almost impossible for plant personnel to maintain them on top performance. Additionally, determining a feasible operating region within acceptable variable ranges and optimal performance is a difficult task in process engineering; therefore, several works investigate the correlation between performance criteria and controller parameters or structure. For instance, using the knowledge from the feasible operating region to design the controller structure for a flash distillation process, where the improved design outperforms the classical configuration[12].
The use of the design of experiments (DoE) methods, such as the response surface methodology, as a design tool, is widely accepted to be a powerful approach to simultaneously optimize complex processes in terms of various response variables, for instance, system performance and energy consumption[13, 14]. The response surface methodology can also be used together with simulation studies to investigate the effects that factors have upon response variables[15].
In this work, a novel experimental-based approach to reach an optimal performance is proposed. The core of our method is DoE. The flow control process from the TecQuipment's Process Trainer is used in a two-stage method: first, a two-level factorial experiment design with n factors (2n) was applied to compare different control schemes. The scheme comparison is carried out in terms of energy consumption and closed-loop performance. For the best relative scheme, a central composite face-centered (CCF) design was completed obtaining controller parameters which optimize performance, in terms of the integral absolute error (IAE) index, while operating in a region of lowest energy consumption. Notice that it is not necessary to develop a complex first principle model of the process to be controlled, enabling the use of our approach in industrial process plants. This work’s main motivation was to propose an experimental approach to find a controller parameter within an acceptable search space, which yielded an optimal system response regarding variables related to the system outputs. In the case presented, using the response surface methodology and defining the limits of the search space with a traditional tuning method, optimal controller parameters were found with respect to the response variables IAE and energy consumption.
2. Methodology
In this section, a case study is presented, where a control scheme is selected, and the optimal tuning of a flow control loop is performed, for which experimental data collected from plant operating conditions.
2.1 System description
The prototype plant CE117 Process Trainer from TecQuipment (see Figure 1] was utilized to validate the proposed approach.
The CE117 Process Trainer is a fully integrated laboratory-scale process control plant equipped with valves, pumps, power supplies, and ancillaries to allow the implementation of flow, level, temperature, and pressure control strategies. More precisely, in the flow control loop, the prototype plant consists of a reservoir tank from which water is lifted by a hydraulic pump (P1) into a process tank; in this line, a servo-controlled proportional valve (V1) and a flow transmitter (FT) are situated. Additionally, after the pump, there is a process loop bypass valve (V2), which will be used within the framework of this study to simulate disturbances due to leaks. The piping and instrumentation diagram (P&ID) describing the process under study is presented in Figure 2. The drivers of the components of the plant use analog signals with a range from 0.0 to 10.0 Volts. Further technical data are presented in Table 1.
2.2 Control Schemes
Two actuator-based control strategies were considered for the flow control loop of the process: in the first one, the actuator of the final control element is the pump (P1). In contrast, in the second one, both the pump (P1) and the proportional valve (V1) are considered as actuators. In both cases a proportional-integral (PI) controller was considered.
Control schema 1: in this scheme, the hydraulic pump is driven by the PI controller while the proportional valve is held open with its driver at a constant value of 8.0 V; in Figure 3, a piping and instrumentation diagram of this scheme is presented.
Control schema 2: in this case, both the pump and the proportional valve drivers are manipulated by PI controllers, with flow being the controlled variable in both cases. The piping and instrumentation diagram of this strategy is shown in Figure 4.
2.3 Benchmark Process
To evaluate the control strategies regarding both energy consumption and closed-loop performance, a setpoint signal consisting of a sequence of three steps with amplitudes of 5.0 L/min, 2.0 L/min, and 3.0 L/min, respectively, with a total duration of 150 seconds was established as the benchmark. Figure 5 shows the setpoint signal. To assess energy consumption, a Belkin WeMo Insight Switch is used to obtain two instantaneous power measurements during each cycle.
The power measurements are averaged and multiplied by the process duration to calculate energy consumption (Ec) in [W/h]; this is one of the process variables analyzed in the DoE. Considering that the energy consumption of the pump is significantly higher than that of the valve, the controller for the valve is tuned and kept invariant throughout this work. In contrast, the controller for the pump is investigated using the proposed methodology.
2.4 Tuning for the Valve PI-Controller
A process step test was carried out as follows: 1) with the system in open loop, a step change in the manipulated variable was applied. It is important to remark that the magnitude of the change should be large enough to generate a measurable change in the transmitter signal, in this case, a change in the valve driver is made from 2.0 V to 9.0 V, while keeping the pump driver at 8.0 V. 2). The response of the transmitter output signal is recorded, making sure that the resulting plot of the controlled variable versus time covers the entire test period from the introduction of the step test until the system reaches a new steady state. Using the output response of the plant, i.e., liquid flow as a time series, the dynamic behavior of the system can be identified. In this case, the maximum rate of change can be observed as soon as the input step was applied, with a small time-delay. This response can be modeled as a first-order system plus dead time; for this reason, a linear model was identified with a First-Order-Plus-Dead-Time (FOPDT) structure using the MATLAB System Identification Toolbox. The model is described by the transfer function in (1), and the model and real plant response are plotted in Figure 6.
The model was then used to find the parameters for the PI Controller of the valve. With the help of the interactive PID-Tuner interface in Matlab, the gains in the controller are tuned to obtain closed-loop stability, adequate performance, and robustness[16]. In a parallel configuration, the gains for the PID are set to kc = 3.0 and ki = 1.9, which results in a not too aggressive control of the flow via the valve. For a unit step, the closed-loop model had a rise time under 3 seconds, a settling time under 10 seconds with an overshoot of less than 3%.
A FOPDT model is obtained for the pump (2), with a procedure like the one used to obtain the valve model, varying the pump driver from 2.0 V to 7.0 V.
For the pump, tuning is accomplished using the rules of Internal Model Control[17]. Before presenting this procedure, the DoE methodology must be introduced, considering that the value of the tuning parameter is selected according to the experimental conditions described in the DoE methodology.
2.5 DoE Methodology
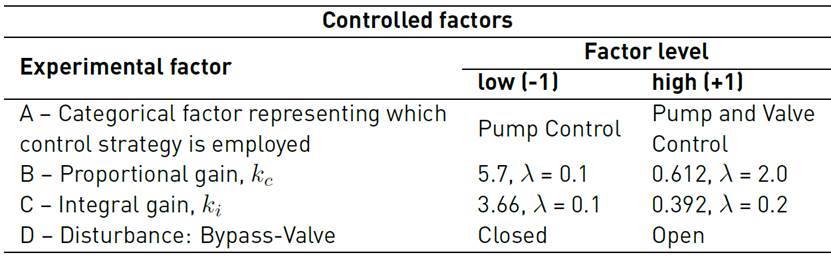
A full factorial (24, n = 1) experiment with two levels for each factor is conducted initially to screen for significant factors. The experimental conditions are shown in Table 1. Based on the results, a Central Composite Face-centered (CCF) is carried out and examined in section 3, to determine optimum areas of operation from which a new operating point is proposed and tested in the real plant.
The coded (1) and (-1) PI-controller gains k c and k i , in a parallel configuration, are obtained by varying the parameter λ from the tuning rules by internal model control[17-19]. Both values for the parameter λ (0.1 and 2.0) yield acceptable process closed-loop performance. The equations for a PI-Controller are given by Equation (4), and ki = kcτ in the PI parallel configuration. The values of kp = 0.760, τ = 1.560 and t0 = 0.200 refer to the FOPDT model in (3) and (4).
Thus, the natural values for Factors B and C, are found and shown in Table 2 for the complete set of Factors.
3. Experiments
The factorial experimental design and the results for both process variables are presented in Table 3, in the randomized order of the runs. Data analysis was performed using the software Statgraphics Centurion XVII.
3.1 Screening energy consumption
Before discussing the results of the analysis of variance (ANOVA), the assumptions of normality, homogeneity of variance, and independence of the residuals were tested for both process variables (Appendix).
Consequently, after examining the normal probability plot of the ANOVA, interactions with a low level of significance were removed from the analysis of variance sequentially. Factor B, its interactions, and the interaction between Factor C and D are excluded from the ANOVA, thus remaining with the factors shown in the ANOVA results in Table 4.
From the ANOVA results, the factors with higher effects are A and D, which can also be seen in Figure 7.
It could be inferred apriori that Factor D plays a significant role in energy consumption. When the bypass valve is opened, to maintain the same flow setpoint, a higher energy input is necessary. For Factor A, the performed analysis suggests that the pump and valve control scheme has lower energy consumption. It furthermore shows that the integral gain on the controller affects both controller schemes differently in terms of energy consumption.
3.2 Screening closed-loop performance
A similar procedure is conducted with the results of the ANOVA using the normal probability plot for the IAE, and sequentially excluding interactions and factors with low levels of significance. It is concluded that based on the conducted experiment, only Factor B has a significant effect on the closed-loop performance in terms of the IAE, as can be seen in the Pareto in Figure 8.
3.3 Central Composite Face-centered (CCF) DoE
According to Montgomery[14], the Response surface methodology (RSM) is a set of powerful statistical techniques that can be used to model problems where one or many independent variables are influenced by several other variables. The analysis of problems using this method can optimize these response variables, where the analytical nature between the response variables and the independent variables is unknown. Normally, a low order polynomial in the region of interest defined by the independent variables is used to investigate the relationship. The CCF is a class of DoE and is the most popular design structure to identify second-order models, where the curvature of the independent variable is of interest.
Based on the conclusion drawn from the previous screening experiment, the relation between factors B and C for the pump and valve control scheme is further explored, i.e., Factor A equals 1 and fixing the bypass valve to closed; thus, Factor D equals -1. A CCF design is completed with axial points located at the centers of the faces of the squared region, defined by the experimental conditions used in the screening experiment, with two central points. The new experimental conditions associated with Factors C and D equal to zero are found by interpolating the parameter λ from the tuning rules by internal model control (IMC). For the region between the coded values -1 and 1 and natural values 0.1 and 2.0, respectively, the center yields for the coded value 0, the natural value λ = 0.95. Following the IMC tuning rules with the new parameter λ, the new levels for the factors are found to be kc = 1.210 and ki = 0.774. The CCF design with the values for the output variables is presented in Table 5.
Using the ANOVA results to analyze the response variable energy consumption, first interactions among factors are sequentially eliminated, and the ultimately factor B is removed from the analysis of variance. It is clear that the information extracted from the ANOVA, presented in Table 6, indicates that the Integral Constant of the PI-Controller significantly affects the consumption of energy. That can be explained with the impact of changing the slope with which the response moves towards the reference, when this tracking is slow for small values of the parameter K i , in this case towards the point Factor C equal to 1, consumption increases as seen in Figure 9.
Adjusted R-Squared = 68.33 %
The results of the ANOVA for the IAE response, after removing the interactions with a low level of significance, are shown in Table 7. The response surface plot resulting from the regression model of the analysis is shown in Figure 10.
Adjusted R-Squared = 77.10 %
3.4 Analysis of the results
The operating conditions that minimize the estimated IAE are shown in Table 8, with their coded values, and in Table 9, their mapped natural values are listed.
The found optimal operation conditions are then tested in the real process, obtaining the results for Energy consumption and IAE shown in Table 10.
The closed-loop response of the real system using the optimal operating conditions for the controller gains is shown in Figure 11, and the authors qualify it as an excellent performance. The control effort for the pump and the proportional valve using the controller gains for the optimal operating condition are shown in Figure 12.
The closed-loop performance of the experimental condition corresponding to the CCF run number 8 is better in terms of the IAE; However, its energy consumption is higher since consumption is highly correlated to the control effort of the pump. In Figure 13, the control effort for both experimental conditions, CCF-Run 8, and the optimal operating point are presented. Notice that the pump control effort for the experimental condition deemed optimal by the regression model and the response surface methodology is considerably lower than the control effort for the CCF-Run 8.
4. Conclusions
The response surface methodology (RSM) is a mighty collection of techniques that, if used appropriately, become tools to optimize complex processes where several response variables are affected by numerous identified factors. The statistical information abstracted from the data collection representing a stochastic and even dynamic process allows the methodology’s user to explore the true response function. Regression models manage to extract the natural error of the system and perform system optimization without analytically determining the complicated relationship between response variables and factors of influence.
An objective parameter to compare the energy consumption of two different control architectures was proposed. Following a DoE approach for the assessment, two-level factorial experiments were used for screening Factors, and a comparison of controller schemes was completed in a real process.
Within this work, the RSM was used successfully to minimize two variables of interest, Energy consumption, and closed-loop performance, of a specific process, by exploring the gains in a controller as Factors. The found optimal operating condition is tested in the real system. The regression model predicted at the optimal operating conditions an
 =15.33, and the real system responded with an IAE=15.92. The difference between them is only 3.8%, with energy consumption considerably lower than most of the operating conditions explored in the data collection process. This is a clear indication of the benefits of the proposed approach.
=15.33, and the real system responded with an IAE=15.92. The difference between them is only 3.8%, with energy consumption considerably lower than most of the operating conditions explored in the data collection process. This is a clear indication of the benefits of the proposed approach.
The regression model from the proposed methodology found controller parameters, which were used as a new experimental condition. Subsequently, using these parameters for the controller, the response showed a lower control effort than all the other experimental conditions. This was because the control effort for the pump in this new experimental condition required a lower voltage causing lower energy expenditure. The proportional gain was set close to one of the boundaries causing a fast response to the step changes followed by a smooth error elimination phase whose rate depends on the integral time.