In some articles published the Benford´s or first-digit Law was proposed as a cost effective tool to evaluate data in biomedicine, medicine and public health ^{1), (2), (3), (4), (5), (6} (see Figure 1). Its use could be very important in sanitary emergencies as COVID-19 epidemic, when rapid evaluation of epidemiological surveillance systems require to be evaluated ⁷. Since the use can be controversial when only few data are available (n<7), we developed a new exact test to screen the fulfilment of Benford distribution. Under this law, the expected number digits for sample sizes varying from n=1 to 6 are in Table 1. In this case we assume that data come from an independent sequence of events (i.e., the occurrence of any particular digit doesn’t depend on the occurrence of any previous one). For this particular case, it can be used according with the known probabilities given by Benford, and using it as the scenario corresponding to the H0: “the data are Benford’s law distributed”. It can be expressed with the equation:

Where

Figure 1 Fulfilment of Benford´s law of data on COVID-19 outbreak from Chinese provinces, regions and cities - situation report 17 (n=34). 

Table 1 Expected occurrence of first digits following Benford distribution with small sample sizes 

Table 2 Fulfillment of Benford distribution by American countries reporting few data during the influenza A(H1N1) outbreak (epidemiological weeks 13-47, 2009). 

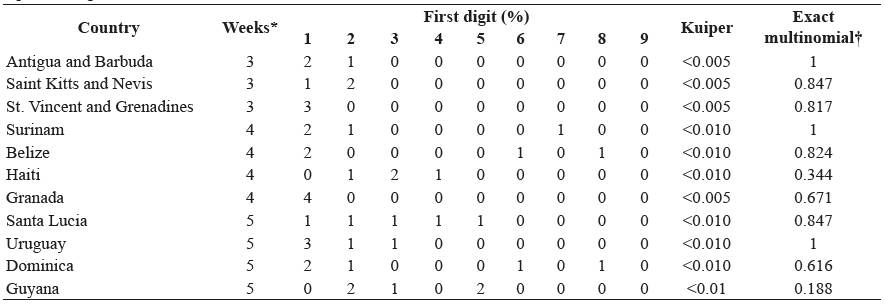
* Only weeks with report (one or more cases) to the Pan American Health Organization.

† estimated with EMT package.

Naturally, data coming from no-Benford distribution are less probable to appear distributed like that, and consequently are more likely to reject the H₀. Thus, the analysis does not depend on the sample size.

To observe the performance of this test we used data with small sample sizes (n<7) from a previous publication ⁶. This test was implemented in the R package, using the code: dmultinom(x = c(#1,#2,#3,#4,#5,#6,#7,#8,#9), size = NULL, prob = c(0.301, 0.176, 0.125, 0.097, 0.079, 0.067, 0.058, 0.051, 0.046)), where #i represents the absolute frequency of the correspondent digit i=1,.. 9. With this procedure we obtained exact probabilities. After, p values were calculated with the EMT package developed by Menzel⁸ using the code: observed <- c(4,1,0,0,0,0,0,0,0) # observed data: underH0 <- c(0.301, 0.176, 0.125, 0.097, 0.079, 0.067, 0.058, 0.051, 0.046) # underH0 out <- multinomial.test(observed, underH0) # p.value, where #i represents the absolute frequency of the correspondent digit i=1,.. 9. Comparisons with Kuiper´s tests were realized ⁹.

With the new statistical test is possible to extend the use of Benford´s law to biomedical, medical and public health areas with small sample sizes.