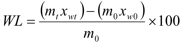INTRODUCTION
Mango (Mangifera indica L. Filipino variety) is one of the most likeable tropical fruits around the world, due to its taste, smell, color, and nutritional value. It is widely used as a fresh fruit, ripe, and in processed products as ingredient in fruit salad, ice cream, jam, yoghurt, and cakes, among others 1. However, green mango is also used as a fresh and processed product. In some countries, mango is used to prepare different processed products as drinks, cocktails, candy, processed meats and vinegar (chutney) and powered products 2,3.
In Colombian the consumption of fresh green mango (also known as mango “biche”) is quite popular, and is consumed with lemon juice, salt, and honey. The acidity, color, and texture of the green fruit, provides to the consumers, agreeable taste. However, its high humidity content (0.83 ± 0.03 wb) and high water activity (aw), (0.983 ± 0.005) 4, makes of mango a highly perishable fruit, thus requiring conservation alternatives 5. Osmotic dehydration (OD) is an interesting alternative for the conservation of diverse vegetal products, since it is a non-thermal and low-cost process 6. The technique consists in partial water removal from a product soaked in a hypertonic solution; this removal is due to the driving force resulting from the difference of osmotic pressure and aw existing between the medium and the product to be dehydrated 7,8. Along OD, three simultaneous current flows take place: a water flow from the product’s interior toward the surrounding medium, a flow of solids, from the osmotic solution (OS) toward the product, and a third flow from inherent solutes of product (sugars, organic acids, minerals, and vitamins) toward the OS, which is quantitatively smaller 9. In OD, binary OS have been traditionally used (solute + water) and ternary OS (2 solutes + water), however, more water removal can be achieved using ternary OS, which leads to the improved organoleptic properties of dehydrated products 10-12. Sucrose and NaCl are widely used in binary and ternary solutions to osmotically dehydrated products such as apple 13, melon 14, tomato 12, carrot 15, and banana (16. Scientific literature reports several studies with different conditions of process of OD of ripe mango 1,7,9,17-19. However, no research about green mango OD has yet been reported. The purpose of this study was to evaluate the dehydration kinetics (in terms of water loss, solutes gain, and weight reduction) and the quality parameters, aw, and volume in green mango samples (Mangifera indica L.), along the OD process, using ternary solutions of sucrose at 40% and NaCl at 3, 6, and 9%.
MATERIALS AND METHODS
Samples preparation
Green mango samples (Mangifera indica L. Filipino variety), with maturity scale zero, and with similar characteristics (color, and size) were used. The fruit was purchased at a local market in the municipality of Palmira (Valle del Cauca Department - Colombia), washed with potable water, peeled with a stainless steel knife, and cut into cylindrical samples (15mm diameter and 15mm height), perpendicular to the axial axis of the fruit by using a cylindrical stainless steel punch.
The OD Process
Ternary OS were prepared in distilled water, NaCl, and commercial sucrose, with a volume of 10 L each. Four OS, one sucrose solution at 40% (40°Brix) (w/w) without the addition of NaCl, and three sucrose OS at 40% (w/w) with NaCl addition (w/w) in concentrations of 3, 6, and 9% were used. OS of 40ºBrix + 0% NaCl (40-0), 40ºBrix + 3% NaCl (40-3), 40ºBrix + 6% NaCl (40-6), and 40ºBrix + 9% NaCl (40-9) were obtained. The samples were immersed in the different OS at 30 ± 0.5ºC which had been prepared in plastic container. Then OS were constantly shaken at 800 rpm by using a mechanical shaker (Ika Labortech Nik, US), in order to prevent crusting resulting from the presence of the solutes in the surface of the samples. The ratio fruit - OS, in terms of weight, was 1:20 to guarantee a constant concentration of the OS along OS 20,21, thus avoiding reduction in the driving force of the osmotic process 22.
In each osmotic process samples were taken out at different times of OD (15, 30, 60, 90, 180, 240, and 300 m.), in other to verify weight (m), soluble solids (x s ), humidity mass fraction (x w ), a w , and volume (V). Once the samples were taken out of the OS, they were quickly washed with distilled water, in order to eliminate external remnants of OS, and immediately dried, using absorbent paper. Three replicates of each treatment were performed.
Mass transfer kinetics
The weight reduction (WR), water loss (WL), and solutes gain (SG) of the samples by means of Equations 1, 2, and 3, respectively were calculated.
Where m is the mass of the sample, and x w and x s are the humidity mass fraction and soluble solids fraction of green mango, respectively. Subindexes 0 and t refer to the initial condition of the fruit (fresh state) and to its condition after certain time t of OD, respectively. For each osmotic treatment, mass balances were performed using equation 4, in which the summation of the net losses and gains of water and solutes (Equations 2 and 3, respectively) are compared with the weight reduction of the samples (Equation 1)
Effective Diffusion (D ef )
In order to calculate water D efw and solid D efs, the analytic solution of Fick’s second law was used. The Fick’s second law was applied to finite cylindrical geometry, diameter 2r and height 2l, which is solved by means of Newman’s rule, considering the juxtaposition of a finite cylinder (Equation 5) and finite plane plate (Equation 6) 23:
Where x jt ; x j0 , and x je are the humidity content (x wt ; x w0 and x we ) or solutes contents (x st ; x s0, and x se ) of the samples. Subindixes 0, t, and e are the initial time of the fruit (fresh fruit), at a time t of OD and the equilibrium condition, respectively. r is the radio of the cylinders. δ are the roots of Bessel function, first class, and zero order. And Foj is number of Furrier to mass transfer, for water (Fo w ) and solids (Fo s ) (Equation 7). D ef j is the effective diffusivity(m2/s) of each component (D ef w y D ef s ) and l is half the height of thecylinders studied.
From the conjugation of 5 and 6 Equations, the number of Fourrier, for each OD time, was calculated. And by means of a Fo vs. t graph, D ef was determined. D ef was isolated from the slope of straight line 16,24.
Analytical determinations
In order to calculate WR, the samples were weighed before and after OD, using an analytical balance (Mettler Toledo AB204 Model, 0.001g precision). The humidity content (MC) through the gravimetric method 20.013 of the AOAC for sugar-rich fruits was measured. x s were determined by measuring the refractive index of the liquid phase extracted from the samples, using a refractometer (Attago RX-7000) at 20° C, with a ± 0.5° precision. The a w was measured with a Dew Point Hygrometer (AquaLab 4TE), with a 0.0003 sensibility. The volume of the samples was calculated by using a digital gauge. With the gauge the height and diameter in three points at 120° of the circumference of the samples were measured. The measure of the volume was used to determine the Shrinking Coefficient (SC), based on Equation 8, which relates the volume of the cylindrical samples before (V o ) and after a time t of OD (V t ) 25.
Statistical Analysis
The effects of the concentration of the osmotic solutions on OD kinetics, aw and volume of green mango samples was found by means of a fully random variance analysis (ANOVA), with 95% confidence. The analyses were run by using the SPSS 18.0.0 (PASW Statistics 18) statistics program.
RESULTS
The fresh green mango samples showed an average 90.27 ± 1.10% MC; soluble solids of 7.33 ± 0.43% and a w of 0.9969 ± 0.0022. The values correspond to the average of 12 lots.
Mass transfer kinetics
The evolution of WL and SG in dehydrated green mango samples subject to different osmotic treatments is depicted in Figure 1. For a better visual effect of the curves, error bars in each point are not shown. Yet, the standard deviation fluctuated from 0.05 to 2.04% for WL and 0.10 to 1.91% for SG.
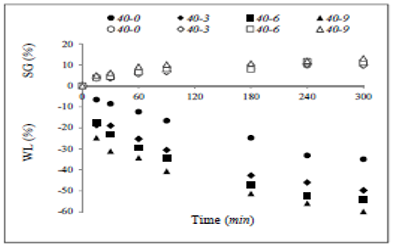
Figure 1 Water loss kinetics (Black symbols) and solutes gain (white symbols) of dehydrated green mango samples treated in different osmotic solutions.
Figure 2, depicts the evolution of WR in the different treatments along the osmotic process. As can be noted, there was weight loss in all the treatments along OD time. The ANOVA showed a significant effect (p<0.05) of NaCl addition on WR.
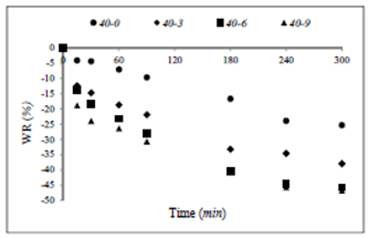
Figure 2 Weight reduction as a function of OD time for green mango samples in different ternary solutions.
Figure 3, depicts the relationship between WR and (WL+SG) (material balance). The curve slopes adjusted to the experimental points showed values close to one in the different treatments (varying from 0.9006 to 1.0067).
Water activity variation
Figure 4, shows the changes in a w in osmotically dehydrated green mango samples in different treatments. The statistical analysis showed a significant effect (p<0.05) of NaCl solution concentration on a w . At the end of the OD process (300 min.), the samples binary treatment (40-0) reached a w value of 0.9828 ± 0.0008, while the ternary samples (40-3, 40-6 and 40-9) reached values of 0.9709 ± 0.0007, 0.9309 ± 0.0052 and 0.9063 ± 0.0001, respectively.
Determination of Shrinking Coefficient (SC)
In Figure 5 the SC of the green mango samples at different times of OD in binary and ternary solutions are depicted.
When comparing the different treatments, significant differences (p<0.05) are found between treatments 40-0 and 40-3, and between treatments 40-3 and 40-9, while there was no statistically significant difference (p>0.05) between the other treatments. Although there was no difference between the ternary and the binary treatments, binary treatment 40-0 (dotted line in Figure 5.) shows slightly lower values of SC when compared with ternary treatments, thus reaching a value of 0.3137 ± 0.0067 at the end of the process, while ternary treatments reach values higher than 0.3638.
Estimation of Effective Diffusitivity (D ef )
Table 1, depicts the values of the effective diffusion coefficients in the osmotic processes, for water transport (D efw ) and solids transport (D efs ). In calculating these coefficients, the first five terms in each series were considered (Equations 5 and 6), in order to obtain greater convergence of model convergence 33. The mass fractions of water and/or soluble solids of the different OS were used (since when t → ∞; x w fruit = x w OS and x s fruit = x s OS ).
Table 1 Humidity diffusion coefficients (D efw ) and solutes diffusion coefficients (D efs ) along OD of green mango samples in different ternary solutions.
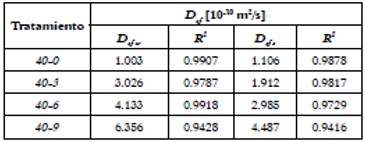
The diffusion coefficients for water varied from 1.003 to 6.356 x10-10 m2/s and from 1.006 to 4.487 x10-10 m2/s for solids. Both coefficients (D efw and D efs ) showed a magnitude order of 10-10 m2/s. The ANOVA showed a statistically significant effect (p<0.05) of the NaCl concentration of the OS on the D efw and D efs .
DISCUSSION
Mass transfer kinetics
As expected, WL and SG increased in all the osmotic treatments, along process time. A significant effect (p<0.05) of NaCl addition to the sucrose solution at 40°Brix on WL was observed, because a higher salt concentration yielded a higher WL, during all process time. At the end of the OD process (5h), the samples in treatment 40-0 reached WL equivalent to 34.94 ± 0.80%, and when adding 3, 6, and 9 of NaCl to the OS of 40-0, the WL increased to 49.80 ± 0.32, 54.16 ± 1.67 and 59.82 ± 1.18%, respectively. Similar findings have been reported for different osmotically dehydrated vegetables (12, 14, 15, 26). This behavior suggests a synergic effect between sucrose and NaCl in the ternary solution, with an osmotic potential greater than that of the binary solution 18. Sacchetti et al.27 report that the chemical potential of ternary solutions increases with the increase of the solutes concentration. Therefore, the addition of NaCl provides a larger gradient of osmotic pressure, which intensifies the driving force necessary for mass transfer in the OD 12. As to the specific influence of NaCl, it can produce some structural changes in the cell membrane of the fruits, raising its permeability 26. Lenart and Flink 28 found that since the molecular weight of NaCl (58.49 g/mol) is lower than that of sucrose (342.29 g/mol), NaCl is easily dissolved through the cytoplasmic membrane of vegetable cells, thus creating concentration gradients in the vacuoles and cytoplasm, which allows for more water extraction from the cells 14,29. On the other hand, sucrose molecules easily accumulate on the cytoplasm surface, hampering mass transfer (known as “Crusting Phenomenon”). In ternary solutions, however, the presence of NaCl prevents this phenomenon and, consequently, facilitates water flow 27-29.
In the case of SG (Figure 1), all treatments show soluble solids gains along OD. However, and according to the ANOVA and Tukey assay/test, there was a statistically significant different (p<0.05) only between the treatment with a more-concentrated OS (40-9) and the other treatments (40-0, 40-3 and 40-6). At the end of the process (300 min), the sucrose treatment (40-0) reached 10.86 ± 0.97% of SG, while the ternary treatments 40-3, 40-6 and 40-9 reached SG of 9.87 ± 0.62, 11.05 ± 0.56 and 13.10 ± 1.66%, respectively. It can be said that in all treatments there were fast SG in the first 90 min of the process. The rapid SG at the beginning of the process may be due to the high driving force existing between the OS concentration and the liquid phase concentration of the fresh sample 30. Likewise, the slow SG following the first 90 minutes of the process may be caused by the presence of sucrose on the surface of the fruit, which prevents solutes from getting in 31, and probably provokes the crusting phenomenon 28.
WR (Figure 2) is a parameter including the net balance of flow of water loss and solute gains along the osmotic process. Therefore, the sum of these two countercurrent flows leads to the net mass variation of the dehydrated samples 32.
The ANOVA showed a significant effect (p<0.05) of NaCl addition on WR, which means that the greater the NaCl concentration, the higher the WR. At 300 min of OD, binary treatment 40-0 yielded the smallest WR of 25.32 ± 0.02%. Rodrigues and Fernandes 14 and Bambicha et al.33 report similar findings in watermelon and pumpkin, respectively. Referring to Figure 3, the values for R 2 (from 0.9927 to 0.9994) indicate the reliability of the experimental data of the osmotic process.
Water activity variation
It is observed that the dehydrated samples with ternary solutions showed greater decrease in aw, when these are compared with the samples the binary treatment.
The variation in the a w (Figure 4) are associated with the WL and SG explained in Figure 1, above. According to 34, a w can be reduced by increasing the concentration of solids in the liquid phase of the samples, be it through water extraction or through the addition of new solutes, and the existence of salt in the hypertonic solution obstructed the formation of compact surface layer, permitting higher rates of solid gain and water loss. The increase in salt concentrations lowered the water activity of the solution with elevated driving (osmotic) force. Similar findings are reported for osmotically-dehydrated potato 30.
Determination of Shrinking Coefficient (SC)
Low values of SC indicate a greater volume loss, while high values indicate lower volume changes or lower shrinking associated to higher conservation of the integrity of the dehydrated product.
There is significant decrease of the SC in all the treatments along the OD time. This behavior is associated with water loss and solute gains along the osmotic process. Viberg et al.35 indicated that the deformation of the product in the OD process depends on the flows of water and solutes inside the product. Mayor and Sereno 36, argues that the shrinking of a dehydrated product increases with the volume of water extracted from it, since at a greater water extraction there are higher concentration tensions, which weakens the product’s structure.
The samples in ternary treatments underwent slightly less volume changes than the ones in binary solutions (40-0). These findings suggest that the combination of NaCl and sucrose in the OS leads to a protecting effect of the solid structure of the product, which would imply that a solutes mixture accelerates mass transfer kinetics and reduces a w, without contributing to the shrinking of osmotically dehydrated green mango. Similar findings for have been reported for pumpkin OD 37.
Estimation of Effective Diffusitivity (D ef )
Coefficients D efw and D efs showed a magnitude order of 10-10 m2/s, which is within the interval of dehydrated foods (10-12 y 10-8 m2/s) 8. Similar results have been reported for other osmotically dehydrated fruits and vegetables, such as pineapple 38, apple 39, yellow pitahaya 6 and banana 16. A good linear adjustment of treatments 40-0, 40-3 and 40-6 is evident, with R 2 values higher than 0.97, as well as a reasonable adjustment of treatment 40-9 which is higher than 0.94. Both diffusion coefficients increase as the NaCl concentration of the OD increases, facilitating the mass transfer of water and solutes of the food. In other words, there is a decrease in the matrix resistance of the green mango samples to diffuse water and solutes. Chiralt et al.40 found that a greater concentration of solutes in the OS increases the effective diffusion coefficient. At the same time, the synergic effect between sucrose and NaCl to increase the diffusion coefficients of the mango samples treated in the ternary OS, noticeable in comparison with what was found when they were dehydrated in a binary solution. Mercali et al.16 contend that the presence of NaCl in the OD affects the mechanism involved in the simultaneous elimination flows of water and solutes infiltration, thus affecting the diffusion coefficients.
When comparing the diffusion coefficients of water and solutes in the ternary treatments, it is observed that the ones for Defw higher than those for D efs , which indicates a greater speed (less resistance) in water transport. Qi et al.41 state that the addition of NaCl to the osmotic medium that already contains sucrose reduces the formation of the dense superficial layer that limits water transport. This behavior suggests that in the OD mango matrixes in ternary solutions water transport predominates over solids transport. As to binary treatment (40-0), the D efs coefficient was slightly higher than the D efw coefficient. This may be explained in light findings by Nsonzi y Ramaswamy 42 who think that there may be a progressive formation of sucrose layer on the surface of the food which hampers water exit from the sample along the osmotic process crusting phenomenon.
CONCLUSIONS
This research showed that binary (sucrose + water) and ternary (NaCl + sucrose + water) solutions, are suitable for dehydrating green mango (Mangifera L. Filipino Var.), however, the ternary solutions were more effective, due to the green mango samples had higher WL, SG and WR, decreased aw, less loss of volume, and higher water and solutes diffusion coefficients. In all the treatments, water loss was greater than the solute gains, (maximum 62% loss in treatment 40-9); this suggests that ternary solutions in OD could be a technique for optimum processing of green mango samples, serving as pre-treatment for other agro-industrial process.