Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.31 Bogotá Jan./Jun. 2010
Renovación priorizada de redes de distribución utilizando el concepto de potencia unitaria
Prioritized Renewal of Water Distribution Networks Using Unitary Power Concept
Juan Saldarriaga
MSc. in Hydraulic Engineering. Director, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA). Profesor titular, Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes. Bogotá D.C., Colombia. jsaldarr@uniandes.edu.co
Susana Ochoa
Estudiante MSc. en Ingeniería Civil. Investigadora, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes. Bogotá D.C., Colombia. s.ochoa24@uniandes.edu.co
Mario Moreno
MSc. en Ingeniería Civil con énfasis en Recursos Hídricos. Investigador, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA). Profesor instructor, Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes. Bogotá D.C., Colombia. mariomo@uniandes.edu.co
Natalia Romero
Estudiante doctoral, University of Cornell, Ithaca, USA. Investigadora, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes. Bogotá D.C., Colombia. n.romero32@egresados.uniandes.edu.co
Óscar Cortés
MSc. en Ingeniería de Sistemas. Investigador, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes. Bogotá D.C., Colombia. oj.cortes43@egresados.uniandes.edu.co
Recibido 21 de Octubre de 2008, modificado 23 de Septiembre de 2009, aprobado 30 de Marzo de 2010.
RESUMEN
La operación de redes de distribución de agua potable involucra dos asuntos con grandes repercusiones económicas: la renovación y rehabilitación de tuberías, y la reducción del Índice de Agua No Contabilizada (IANC). Este trabajo presenta un algoritmo que, con base en el concepto de potencia unitaria, permite priorizar los tubos por renovar, de tal modo que se reduzca la potencia disipada y el IANC, se mantenga el plano de presiones nivelado y se encuentre la situación ideal para realizar la renovación en términos de beneficios económicos. Se presentan dos casos de estudio en los cuales la metodología propuesta probó ser eficiente al hallar esquemas de renovación rentables e hidráulicamente óptimos.
PALABRAS CLAVES
Potencia unitaria, redes de distribución, renovación, resiliencia.
ABSTRACT
Water Distribution System operation involves two issues that have large economic repercussions: pipe renewal and rehabilitation and reduction of Non-Revenue Water (NRW). This paper presents an algorithm that, based on the unitary power concept, selects the most important pipes to be replaced in order to reduce the dissipated power and the NRW, while keeping the pressure surface levelld. Additionally, the proposed methodology finds an ideal renewal scheme in terms of economic benefits and profitability. This paper includes two case studies in which the proposed methodology proved to be successful, achieving renewal schemes both profitable and hydraulically optimum.
KEY WORDS
Renewal, resilience, unitary power, water distribution networks.
INTRODUCCIÓN
Con el paso del tiempo, las redes de distribución de agua potable sufren deterioro, lo que desemboca en problemas de capacidad hidráulica reducida, pérdidas de agua, interrupciones en el servicio, deficiencia en la calidad del fluido, entre otros. Adicionalmente, la demanda de agua aumenta con el tiempo y se generan nuevos inconvenientes, como las bajas presiones en los nodos de servicio que son generalmente resueltas mediante el incremento de la cabeza de energía a la entrada del sistema, lo cual, a su vez, aumenta las fugas en la red. Para superar estas dificultades y asegurar continuidad, eficiencia y economía en la operación de redes, es necesario contar con una estrategia de renovación y rehabilitación efectiva. Esta estrategia debe tener en cuenta criterios hidráulicos, económicos, de confiabilidad y calidad del agua [1]; además, dado que los recursos económicos disponibles son limitados, dicha estrategia debe también ayudar a priorizar la inversión que se haga en las redes [2].
En las últimas décadas, se han desarrollado diferentes aproximaciones para solucionar el problema de renovación y rehabilitación de redes de distribución. De acuerdo con [1], estas aproximaciones se pueden clasificar en tres tipos: guías generales de rehabilitación y renovación, modelos de priorización y modelos de optimización. Gran parte de las metodologías desarrolladas hasta la fecha tiene un fundamento principalmente económico y la manera de evaluar la necesidad de mantenimiento y renovación de una tubería es función de la estimación de la tasa o probabilidad de daño, la cual se obtiene a partir de análisis estadísticos sobre patrones históricos de daño [3, 4, 5, 6, 7, 8].
El presente trabajo propone una nueva aproximación al problema de la renovación de redes, que se puede clasificar como un modelo de priorización cuyos principales propósitos son la reducción de fugas, el mejoramiento del desempeño hidráulico y el aumento en la confiabilidad del sistema. A pesar de que las fugas no constituyen un asunto muy relevante en los países desarrollados, éstas son aún un problema significativo en los países en desarrollo, pues en ellos el Índice de Agua No Contabilizada (IANC) puede alcanzar fácilmente valores de hasta 50% [9]. Lo anterior genera grandes desperdicios de agua, energía y químicos de tratamiento; aumenta el riesgo de contaminación del agua debido al contacto con el ambiente [10]; menoscaba la calidad del servicio, produce un impacto negativo en el ambiente y hace más crítico el problema de escasez de recursos hídricos [1].
Para reducir las fugas y mejorar el desempeño hidráulico y la confiabilidad del sistema, la metodología propuesta utiliza la potencia unitaria (PUTi) como criterio para seleccionar los tubos más importantes que deben ser renovados. La potencia unitaria de un tubo i corresponde al producto del caudal que fluye por el tubo multiplicado por la pérdida de energía que tiene lugar en el mismo. Estrictamente hablando, corresponde a la potencia por unidad de peso disipada por fricción y pérdidas menores en esa tubería (nuevo concepto introducido en el presente trabajo). En cada iteración del algoritmo desarrollado, el tubo con mayor PUTi es sustituido por un nuevo tubo con mayor diámetro; el exceso de presión generado con el cambio de tubería se compensa al disminuir la altura piezométrica de la fuente de abastecimiento, de tal forma que el nodo más crítico del sistema tenga exactamente la presión mínima requerida. Así, al reemplazar tuberías y al disminuir la energía en la fuente de manera iterativa, la metodología propuesta pretende reducir y nivelar las presiones a lo largo de la red; esto reduce significativamente las fugas y mejora la eficiencia energética y la confiabilidad del sistema.
DEFINICIONES
POTENCIA UNITARIA DEL TUBO i (PUTi)
La PUTi se define como el caudal que pasa por el tubo i multiplicado por la diferencia entre las alturas piezométricas del nodo inicial y del nodo final del tubo.

ÍNDICE DE RESILIENCIA (Ir)
El Ir es un indicador de la capacidad de una red de distribución para soportar fallas repentinas; este índice fue introducido por Todini [11] y ha sido ampliamente aceptado en la comunidad científica internacional como medida de la confiabilidad de una red de distribución. El Ir se fundamenta en la relación existente entre la resiliencia de un sistema y la cantidad de energía que éste disipa: a menor energía disipada, mayor será la capacidad de respuesta del mismo, debido a que tiene mayor cantidad de energía disponible. En general, un mayor valor del Ir corresponde a sistemas con mayor energía disponible y, por lo tanto, con mayor capacidad de soportar y superar fallas repentinas.
Para determinar el Ir se deben tener en cuenta las fugas en el sistema; éstas son simuladas mediante emisores, cuyo caudal de salida es función de la altura piezométrica en el nodo elevada a un exponente, tal como se muestra a continuación:

donde qf,i representa el caudal de fuga en el nodo i; Cf y xf corresponden, respectivamente, al coeficiente y exponente de emisor o fuga; y hi es la altura piezométrica en el nodo i. Según [10], Cf refleja el tamaño y forma del orificio, y xf la "elasticidad" de éste ante la presión interna; además, ambos parámetros (i.e. Cf y xf) se relacionan. En la modelación de fugas, se emplea normalmente un valor del exponente de emisor (xf) de 0,5, el cual corresponde a orificios de tamaño fijo.
La ecuación utilizada para calcular el Ir considerando las fugas en el sistema es la siguiente:

donde Qi y Hi corresponden al caudal y a la altura piezométrica de cada uno de los ne embalse de la red; qi y hi son el caudal y la altura piezométrica en cada uno de los nn nodos de consumo de la red; y hi,req es la altura piezométrica mínima requerida en cada nodo.
PORCENTAJE DE POTENCIA CONSUMIDA (PPC)
El PPC es una medida de la eficiencia energética del sistema; indica el porcentaje de la energía total disponible que es utilizada para suplir el servicio [10]. En general, mayores valores del PPC corresponden a una mayor eficiencia energética de la red.

En esta ecuación, zmin corresponde a la cota mínima de todos los nodos de la red.
ÍNDICE DE AGUA NO CONTABILIZADA (IANC)
El IANC corresponde al porcentaje de agua que se pierde en fugas o que no se encuentra registrado por la micromedición de un sistema de agua potable.
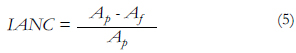
donde Ap es el volumen de agua producido por unidad de tiempo y Af es el volumen de agua facturado por unidad de tiempo.
COSTO DE REHABILITACIÓN POR METRO LINEAL DE TUBO i (Cri)
Puede estimarse mediante la siguiente función (derivada para redes colombianas):
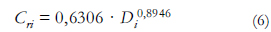
donde Di es el diámetro de la tubería i en mm y Cri es el costo en dólares de 2007 de la tubería i.
RENTABILIDAD (r)
Para analizar la rentabilidad del proyecto, es indispensable determinar el período de amortización de la inversión, el cual corresponde al lapso en el que se espera recuperar el capital invertido en la renovación de tuberías. Para los ejemplos desarrollados, se adoptó un período de amortización de 5 años, un lapso apropiado para recuperar la inversión y que además coincide con el tiempo que comúnmente tardan en aparecer fugas en las tuberías de distribución de agua potable. Teniendo en cuenta que el análisis debe hacerse a largo plazo, la ecuación que define el punto óptimo de inversión es la siguiente:
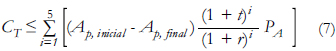
En la anterior ecuación, CT corresponde al costo total en renovación (en dólares de 2007) que se requiere hasta realizar cierto número de cambios de tuberías, AP es el volumen de agua que entra al sistema (calculado para un año), t corresponde a la inflación (alrededor del 6% para Colombia) y PA es el precio por metro cúbico de agua (precio únicamente asociado al costo marginal de producción del agua potable). En general, una buena rentabilidad (r) para una inversión en el sector de servicios públicos se ubica entre el 10% y el 15%.
PROCEDIMIENTO
Los datos de entrada que se tienen para la aplicación de la metodología propuesta son: diámetros comerciales y rugosidades de los tubos con los que se puede renovar la red de distribución existente; costo del agua; coeficientes para determinar el costo de renovación; rentabilidad esperada por la empresa; y período de amortización de la inversión. La metodología se aplica idealmente a una red calibrada, cuyos nodos tienen asignados los exponentes y coeficientes de emisor que representan las fugas del sistema. En las redes analizadas en esta investigación se asignó un IANC uniforme (del 50%), para el cual se estimaron los valores de los coeficientes y exponentes de emisor. El algoritmo desarrollado para llevar a cabo la renovación priorizada de una red de distribución con base en el concepto de potencia unitaria (PUTi) es el siguiente (este algoritmo se implementó en el programa REDES [12]):
1. Se analiza hidráulicamente la red y se incrementa al siguiente diámetro comercial el diámetro del tubo cuyo PUTi sea mayor.
2. Si el tubo ha sido cambiado anteriormente, los coeficientes de emisores en sus nodos no deben ser modificados. Si no ha sido cambiado, se debe observar cuántos tubos llegan al nodo inicial y se debe restar al coeficiente emisor de este nodo la parte que, proporcionalmente, le corresponde al tubo cambiado. El mismo procedimiento se realiza para el nodo final del tubo.
3. Se analiza hidráulicamente la red teniendo en cuenta el cambio realizado en el Paso 2.
4. A la altura piezométrica en el embalse se le resta la diferencia entre la presión mínima en los nodos y la presión mínima requerida (i.e. se resta el exceso de presión que se produjo en la red el aumento de diámetro realizado en el Paso 2).
5. Se calculan los indicadores (Ir, PPC). Igualmente, se estima el costo por reemplazo de tuberías y el beneficio económico generado por el ahorro en agua logrado con los cambios realizados hasta este punto.
6. El proceso finaliza cuando la diferencia entre el valor presente del beneficio y el costo de renovación sea menor que cero, con lo cual la inversión deja de ser económicamente viable, o cuando se cumplan los criterios de parada que el usuario haya definido previamente (e.g. presupuesto máximo disponible para la renovación, rentabilidad mínima admisible). Si ninguna de estas condiciones se cumple, se regresa al Paso 1 y se repite el proceso.
CASOS DE ESTUDIO
RED HIPOTÉTICA R28
La primera red analizada es una red teórica, compuesta por 67 tubos, 39 nodos y un embalse con una altura piezométrica de 100 m.c.a. Esta red tiene una longitud total de tuberías de 9750 m y una demanda media de 0,072 m3/s. Las tuberías son de PVC con rugosidad de 0,0015 mm y diámetros que varían entre 50 mm (2") y 200 mm (8").
Figura 1. Red hipotética R28 con identificador de tubos
SECTOR 35 [13]
Sector 35 es una zona hidráulica del Distrito Capital de Bogotá, Colombia. Su ubicación dentro de la ciudad se presenta en la Figura 2. Bogotá está ubicada sobre una meseta a 2592 m.s.n.m. Esta red está compuesta por 1289 tubos, 1190 nodos y un embalse (tubo de 1800 mm (72") de diámetro) con una altura piezométrica de 2639,77 m.s.n.m. Todos sus componentes tienen un rango de cotas muy homogéneo. Sector 35 tiene una longitud total de tuberías de 39426 m y una demanda media de 0,0605 m3/s.
Figura 2. Ubicación de la red Sector 35 en Bogotá D.C.
RESULTADOS
Todas las redes fueron inicialmente llevadas a su punto límite de presión bajo el escenario de un IANC de 50%, representado en una asignación homogénea de coeficientes emisores en todos sus nodos. Este punto inicial fue diseñado en cada red para un exponente de fuga xf de 0.5, 0.8, 1.0 y 1.5; para cada valor de xf estudiado, se ajustaron los coeficientes emisores de tal forma que el IANC fuera siempre el mismo (50%).
RED HIPOTÉTICA , R28
Es importante destacar que esta red cuenta con una demanda muy alta para la longitud de tubería existente. En la Figura 4 se muestra la variación de la rentabilidad, del Ir, del IANC y del PPC, y el incremento marginal del PPC a medida que aumenta el número de cambios de tubos en la red.
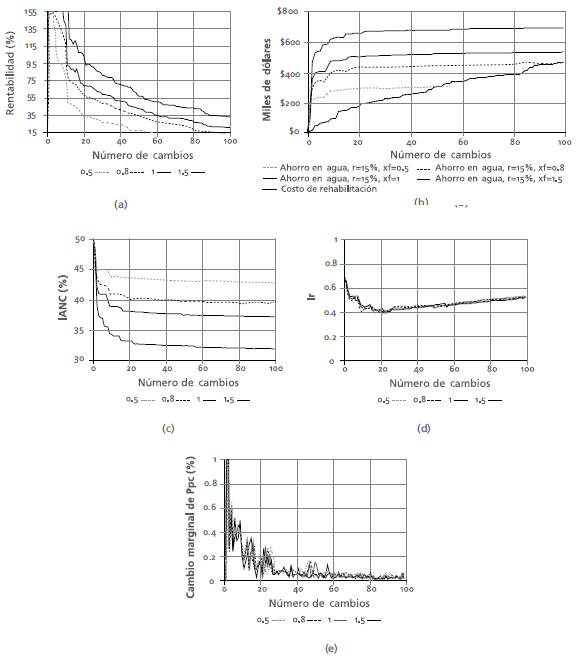
Figura 3. Resultados red R28: (a) rentabilidad, (b) Ir, (c) IANC y PPC, (d) incremento marginal de PPC vs. Número de cambios (para xf = 0,5; período de amortización = 5 años)
En la Figura 3(a) se puede observar que los cambios sobre esta red son muy rentables; esto se debe al alto caudal que maneja. En cuanto al Ir, en la Figura 3(b) se puede ver que este índice aumenta ligeramente al realizar los cambios de tuberías y bajar la altura piezométrica del embalse, tal como se explicó en el procedimiento. El resultado esperado con respecto al Ir era que, al asignar a todos los nodos la presión mínima, éste disminuyera; por lo tanto, es paradójico que el Ir tienda a aumentar. Sin embargo, si se analiza cómo al ir eliminando las grandes diferencias de presión la red se va liberando de patrones rígidos de dirección de flujo, se entiende por qué una red más uniforme puede conservar su resiliencia a pesar de manejar presiones muy bajas en la mayoría de sus nodos. En la Figura 3(c) se muestra que el IANC disminuye de manera considerable, especialmente con los primeros cambios, y que el porcentaje de potencia consumida (PPC) incrementa, lo que indica que se logra un aumento en la eficiencia de la red en cuanto al consumo de energía. La Figura 3(d) puede ser empleada como un indicador del momento en que es conveniente detener la rehabilitación; en ella se ve que, alrededor de los 50 cambios, se produce el último pico en el incremento marginal de PPC, por lo que éste podría considerarse como un punto apropiado para detener el proceso de cambios de tuberías.
SECTOR 35 [13]
Sector 35 es una red con demandas y longitud de tubos altas. En las siguientes figuras se presentan los resultados obtenidos para la red Sector 35; para la cual se hizo además un análisis de sensibilidad para diferentes valores del exponente del emisor xf. La Figura 4(a) y la Figura 4(b) muestran la evolución de la rentabilidad, del valor del ahorro en agua y del costo de rehabilitación a medida que se incrementa el número de cambios.
Figura 4. Resultados red Sector 35: (a) rentabilidad, (b) valor del ahorro en agua y costo de la rehabilitación, (c) Ir, (d) IANC y (e) cambio marginal de PPC vs. Número de cambios (para diferentes xf)
Se puede observar que tanto la rentabilidad como el valor del ahorro en agua cambian significativamente con los diferentes valores del exponente del emisor; en general, a mayor exponente del emisor, mayor es el valor del ahorro en agua y, por lo tanto, mayor es la rentabilidad. Esto se debe a que orificios con altos exponentes de emisor generan caudales de fuga muy grandes; así, al cambiar tuberías con grandes fugas, el ahorro en agua es importante. Otro indicador que tiene una fuerte dependencia del tipo de orificio es el IANC. La Figura 4(c) ilustra cómo, a medida que el xf crece y los orificios son más flexibles, el IANC se puede reducir más con el mismo número de cambios. Este fenómeno explica la mayor rentabilidad en proyectos de rehabilitación de redes con orificios más flexibles.
A diferencia de los indicadores mencionados, existen dos variables que no parecen depender de la variación del xf. La Figura 4(d) y la Figura 4(e) presentan la evolución del Ir y del incremento marginal de PPC con el número de cambios de tuberías. En estos gráficos se puede observar que el tipo de fuga u orificio no afecta significativamente la potencia empleada y disipada por la red (Ir y PPC).
Al realizar el análisis económico del proceso de rehabilitación sobre esta red, se concluyó que el punto óptimo de inversión eran los primeros 55 cambios de tuberías, debido a que a partir de este punto dejan de producirse mejoras significativas en la eficiencia energética de la red y la rentabilidad comienza a ser baja. La Figura 5 presenta el plano de presiones iniciales de la red Sector 35 y la Figura 6, el plano de presiones después de los 55 cambios. Al compararlas se puede ver que la metodología propuesta logró uniformizar significativamente el plano de presiones de la red, lo cual tiene grandes beneficios en términos de eficiencia energética.
Los resultados obtenidos para Sector 35 son buenos e indican que la metodología de renovación basada en la potencia unitaria PUTi puede ser ideal para redes de gran tamaño y aproximadamente horizontales. Se planteó entonces la siguiente hipótesis: la rentabilidad de esta propuesta metodológica para rehabilitar redes radica principalmente en la relación existente entre la longitud de tuberías de la red y la demanda base. Esta hipótesis se comprobó con otras redes reales y se determinó que en redes con demandas pequeñas y gran longitud de tuberías es difícil obtener rentabilidades aceptables.
Figura 5. Plano de presiones inicial de Sector 35
Figura 6. Plano de presiones de Sector 35 después de los 55 cambios
CONCLUSIONES
La aplicación del concepto de potencia unitaria como mecanismo de selección de tubos que se renovarán resulta bastante eficiente en redes de gran tamaño y con longitud de tubería corta en relación con la demanda total. Además de generar esquemas de renovación rentables en estas redes, la metodología disminuye su vulnerabilidad y mejora sustancialmente su eficiencia energética, dado que se alcanza un incremento significativo en el Ir y el PPC, que son indicadores de la confiabilidad y eficiencia energética de la red.
Si bien en redes con gran longitud de tuberías y bajas demandas no es posible lograr que la renovación sea rentable, la metodología propuesta consigue disminuir considerablemente el IANC, lo cual genera grandes beneficios sociales y ambientales.
La rentabilidad de la rehabilitación de una red puede variar considerablemente con el tipo de orificio o fuga; por lo tanto, es importante que la red se encuentre calibrada antes de aplicar la metodología propuesta.
Redes de distribución con superficies de presiones uniformes son más flexibles en cuanto a patrones o rutas de flujo se refiere, lo anterior permite manejar menores presiones en los nodos de servicio, manteniendo un índice de resiliencia (i.e. un nivel de confiabilidad) aceptable. Dado que la metodología propuesta hace uniforme el plano de presiones de la red, los esquemas de renovación que se alcanzan con ésta tienen un Ir aceptable (que incluso puede ser mayor que el Ir inicial de la red) y presiones pequeñas, lo cual lleva a una disminución del caudal de fuga (puesto que éste es proporcional a la presión en los nodos).
El algoritmo de selección de tubos por reemplazar con base en el concepto de potencia unitaria es un algoritmo simple y corto, razón por la que su tiempo de ejecución es muy pequeño en comparación con otras metodologías de renovación existentes.
La metodología propuesta constituye una herramienta útil y eficiente para la planeación y ejecución de obras de renovación de redes de distribución, pues consigue optimizar la inversión en términos económicos y mejora enormemente el comportamiento hidráulico y la eficiencia energética de las redes.
REFERENCIAS BIBLIOGRÁFICAS
[1] M.O. Engelhardt, P.J. Skipworth, D.A. Savic, A.J. Saul and G.A. Walters. "Rehabilitation Strategies for Water Distribution Networks: A Literature Review with a UK Perspective". Urban Water. Vol. 2, No. 2, 2000, pp. 153-170. [ Links ]
[2] D. Halhal, G.A. Walters, D. Ouzar and D.A. Savic. "Water Network Rehabilitation with a Structured Messy Genetic Algorithm". ASCE Journal of Water Resources Planning and Management. Vol. 132, No. 3, 1997, pp. 137– 146. [ Links ]
[3] U. Shamir and C.D.D. Howard. "An Analitical Approach to Scheduling Pipe Replacement". Journal AWWA, Vol. 71, No. 5, May 1979, pp. 248 – 258. [ Links ]
[4] A.J. Ketler and I.C. Goulter. "An Analysis of Pipe Breakage in Urban Water- Distribution Networks". Can. Journal of Civil Engineering. Vol. 12, 1985, pp. 286 – 293. [ Links ]
[5] J.H. Kim and L.W. Mays. "Optimal Rehabilitation Model for Water-Distribution Systems". Journal of Water-Distribution System, ASCE, Vol. 120, No. 5, September/October 1994, pp. 674 – 692. [ Links ]
[6] C.R. Schneiter, Y.Y. Haimes, D. Li and J.H. Lambert. "Capacity Reliability of Water Distribution Networks and Optimum Rehabilitation Decision Making". Water Resources Research, Vol. 32, No. 7, July 1996, pp. 2271 – 2278. [ Links ]
[7] G.V. Longanathan, S. Park and H.D. Sherall. "Threshold Break Rate for Pipeline Replacement in Water Distribution Systems". Journal of Water Resources Planning and Management, July/August 2002, pp. 271 – 279. [ Links ]
[8] Y. Kleiner, B.J. Adams and J.S. Rogers. "Water Distribution Network Renewal Planning". Journal of Computing in Civil Engineering, ASCE, Vol. 15, No. 1, January 2001, pp. 15 - 26. [ Links ]
[9] B. Kingdom, R. Liemberger and P. Marin. "The Challenge of Reducing Non-Revenue (NRW) Water in Developing Countries. How the Private Sector can Help: A Look at Performance-Based Service Contracting". Water Supply and Sanitation Sector Board Discussion Paper Series, Paper No. 8, December 2006. [ Links ]
[10] A.F. Colombo and B.W. Karney. "Energy and Costs of Leaky Pipes: Toward Comprehensive Picture". Journal of Water Resources Planning and Management. ASCE Vol. 128, No. 6. November/ December 2002, pp. 441 – 450. [ Links ]
[11] E. Todini. "Looped Water Distribution Networks Design Using a Resilience Index Based Design". Urban Water, Vol. 2, September 2000, pp. 115 – 122. [ Links ]
[12] CIACUA. Programa REDES. Bogotá: Centro de Investigaciones en Acueductos y Alcantarillados, CIACUA, Universidad de los Andes, 2006. [ Links ]
[13] CIACUA. Proyecto Plano Óptimo de Presiones, Fase I. Bogotá: Centro de Investigaciones en Acueductos y Alcantarillados, CIACUA, Universidad de los Andes, 2001. [ Links ]