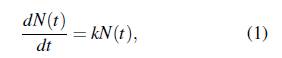1 Introducción
En el transcurso de la historia la humanidad ha pasado por muchas enfermedades víricas, y a pesar de los avances médicos y tecnológicos de las sociedades modernas, estas se han mostrado vulnerables ante la velocidad de contagio del SARS-COV-2. Los datos de brotes tempranos por Covid-19 siguieron en gran medida un crecimiento exponencial [1], evidenciando el poder de transmisión del virus.
En un planeta globalizado es inevitable que los factores asociados a este tipo de dinámica de crecimiento incrementen el riesgo de propagación del SARS-COV-2. En este sentido, el aumento de la población, la creciente urbanización, el turismo de masas, la migración, entre otros factores, determinan el curso de la trasmisión de enfermedades producidas por patógenos, este es el caso del Covid-19. Se sabe que la tasa de casos importados es relativamente baja comparada con la tasa de propagación comunitaria. Sin embargo, cualquiera de estas tasas puede impulsar el desarrollo del brote exponencial. Más aún, entre mayor sean las tasas más rápido iniciará el crecimiento exponencial [3]. En consecuencia, de no haber tomado medidas estrictas de mitigación, el brote se hubiese desarrollado exponencialmente [2].
Una característica que ha incidido en el desarrollo de esta pandemia es la infección subclínica (individuos infecciosos antes de presentar síntomas, e individuos asintomáticos), lo que indudablemente ha causado grandes dificultades para controlar los contagios por Covid-19 [4]. Es decir, la infección subclínica representa uno de los mayores inconvenientes para la identificación de posibles casos diarios confirmados, lo que podría generarar sesgos en el rastreo de casos que jamás fueron confirmados y retrasos en los reportes de casos positivos.
El Ministerio de Salud y Protección Social de Colombia reportó el primer caso de Covid-19, como importado, el 6 de marzo de 2020 en Bogotá D.C. [5]. A partir de esta fecha los casos reportados por Covid-19 empezaron a aumentar significativamente, aunque no de manera exponencial (Figura 2). Las medidas de prevención adoptadas en el país lograron disminuir la velocidad de propagación aplazando el pico de contagios. Sin embargo, la tendencia creciente de contagios diarios conllevó al trabajo conjunto entre las autoridades encargadas de la salud y la economía en Colombia a fin de contener los efectos adversos de la pandemia [6]. Los cuales fueron determinantes a la hora de identificar periodos de crecimiento exponencial, tal y como se verá más adelante.
Existen varios trabajos donde se estudia la curva de contagios, por lo general se enfocan en los casos totales, y en determinar cuál es el modelo que mejor la describe [7, 8]. Se conocen varias técnicas para modelar matemáticamente la dinámica de la Covid-19, una de ellas y la mas sencilla está basada en el ajuste de modelos predictivos de crecimiento poblacional del tipo logístico o exponencial. Estos modelos pueden ser aplicados para analizar el crecimiento de la cantidad de personas infectadas por una enfermedad contagiosa [7]. El objetivo de utilizar esta modelación matemática, consiste en obtener los parámetros de los modelos que mejor se ajusten a los datos reales y predecir la dinámica de contagio.
En este trabajo se utiliza el modelo de Malthus para determinar y analizar los periodos de crecimiento exponencial. La estimación de los parámetros se realiza ajustando el modelo a los datos de la epidemia mediante el enfoque estándar de mínimos cuadrados no lineales [7, 8]. Para la validación del modelo se tendrá en cuenta el coeficiente de determinación R2, la distribución normal de los residuos, y la no indicación de una auto-correlación [9].
Aunque, el análisis estadístico de los datos de contagios diarios por Covid-19 durante la primera ola en Colombia no muestran un crecimiento exponencial a largo plazo, este no se descarta debido a la indisciplina y la falta de acatamiento de las medidas de confinamiento combinados con el sesgo estadístico de las mediciones [8]. Precisamente, este trabajo mostró la existencia de periodos cortos de crecimiento exponencial, por lo general con rangos entre 4 y 5 días, a excepción del quinto periodo con un rango de 36 días (Figura 7).
En la Figura 15 se aprecia que desde el registro del primer paciente con Covid-19, ha venido aumentando la positividad de las muestras tomadas. A partir de mayo se observa como esta supera el 10%, y aunque no existe una respuesta clara frente a cuántas pruebas se deben realizar, la Organización Mundial de la Salud sugiere que los países deben realizar pruebas con el fin de mantener las tasas de positividad por debajo del 10% [6]. Pero, el hecho de que el porcentaje este por debajo de lo recomendado, no significa que el país dejó de presentar crecimientos exponenciales, tal y como se podrá observar en el primer periodo.
De hecho, dentro de la dinámica de transmisión del Covid-19, se ha verificado que la fase de crecimiento exponencial es determinante para conocer la velocidad de propagación del virus [3]. En este aspecto, el interés de este trabajo radica en determinar las tasas de crecimiento y los periodos en los cuales se ha desarrollado esta fase en Colombia.
2 Metodología
Para llevar a cabo este estudio se utilizarán datos disponibles en el sitio web de la universidad Johns Hopkins (la cual sigue en tiempo real la pandemia), la página oficial de la OMS, entre otras. Los datos disponibles en las paginas mencionadas anteriormente se descargan en archivos de formato Excel, con el propósito de crear una base de datos sobre los casos de contagio confirmados diariamente en Colombia. Es importante aclarar que en la página web de la universidad Johns Hopkins se reportan datos desde el 22 de enero de 2020.
Luego, en Excel se crean gráficas de dispersión con líneas suavizadas y marcadores, con el fin de evidenciar empíricamente periodos de crecimiento durante la ola epidemiológica, con rangos mayores o iguales a cuatro días, que puedan ser, o no exponenciales. De esta menera se identifican los posibles periodos de crecimiento exponencial, con su respectiva ecuación (donde incluye su tasa de crecimiento) y coeficiente de determinación (R2).
Como ya se ha demostrado, la propagación de la Covid-19 puede tener un crecimiento exponencial respecto a los casos diarios. En [10], se utiliza la teoría de Malthus para estimar la tasa de crecimiento de nuevos casos diarios de infección por la Covid-19. De manera similar, en este trabajo se aplica el modelo de Malthus y regresiones para estimar las tasas y períodos de crecimiento exponencial de nuevos casos diarios por el nuevo coronavirus que se han presentado en la primera ola epidemiológica en Colombia.
Para ello se supone que N(t) es el tamaño de una población contagiada por Covid-19 en el tiempo t, y que la variación instantánea de la población con respecto al tiempo es proporcional a la población actual, entonces se obtiene la siguiente ecuación diferencial del modelo de crecimiento exponencial (modelo de Malthus)
donde k es la tasa intrínseca de crecimiento de contagios. Suponiendo que en el tiempo inicial la población es N0, se obtiene la siguiente condición inicial
La solución del problema de valor inicial definido por las ecuaciones (1) y (2) está dada por
Para la obtención de los parámetros se aplica logaritmo natural en ambos lados de la ecuación (3) y se llega a la relación lineal entre lnN(t) y t dada por
La ecuación (4) es útil para determinar los parámetros k y N0 a partir de una colección de datos de campo o de laboratorio {ti,N(ti)}.
La estimación de los parámetros se realiza ajustando los modelos a los datos de la epidemia mediante el enfoque estándar de mínimos cuadrados no lineales [7, 8]. De esta forma la ecuación (3) se linealiza en (4) tomando la forma de una ecuación lineal (Y = b + αX), donde, los valores de t corresponden a la variable independiente X, ln N(t) a la variable dependiente Y, y k a la pendiente α.
El modelo se valida por medio del coeficiente de determinación (R2). Por lo general, los periodos cortos tienen un R2 superior a 0,9, sobre todo aquellos que tienen rangos menores a los cinco días.
Para comprender la utilidad de R2 consideremos el siguiente ejemplo: un químico, encargado de realizar una calibración lineal de una pieza de equipo de alta precisión, ciertamente espera experimentar un valor R2 muy alto (quizás superior a 0,99), mientras que un científico del comportamiento, que maneja datos afectados por la variabilidad en el comportamiento humano, puede sentirse afortunado de experimentar un R2 tan grande como 0,70 [9]. En este sentido, se tiene en cuenta un promedio de los valores anteriormente mencionados; por lo tanto, R2 deberá ser mayor o igual a 0,80.
Sin embargo, esto no asegura que el modelo ajustado sea el indicado para los datos obtenidos. Entonces, se tiene en cuenta conocimientos de regresión lineal simple para validar el modelo exponencial. En el modelo de regresión lineal, sus residuos deben tener una distribución normal, además no debe haber indicios de auto-correlación [9]. De esta manera, se tiene en cuenta el valor p arrojado en Statgraphics, en el análisis de varianza (ANOVA), en la prueba de ajuste de bondad Kolmogorov-Smirnov y el del estadístico Durbin-Watson.
3 Análisis de Varianza
Para probar que la línea encontrada en el análisis de regresión se ajusta aceptablemente a los datos, se realiza la prueba de análisis de varianza. El modelo consiste en encontrar la media de los datos de Y, luego separar la diferencia de cada dato menos la media en dos tramos, es decir, la distancia de la media al valor de la regresión (modelo) y la distancia entre el valor de la regresión y el dato (error). Como se mencionó anteriormente, es de particular interés en éste análisis su valor p asociado. Si el valor p es menor a 0.05 (se opera con un nivel de significancia del 95%), lo cual indica la existencia de la relación estadística de la forma específica entre X y Y [11].
El resultado obtenido con el análisis de varianza no garantiza o no valida el modelo ajustado (en este caso el exponencial), por lo tanto, se requiere analizar los gráficos de residuos, y para ello se hace uso del test de Durbin-Watson.
3.1 Test de Durbin-Watson (D)
El Test de Durbin-Watson permite evaluar la existencia de autocorrelación en una Regresión lineal. El estadístico de Durbin Watson es una medida de la correlación serial en los residuos. Si los residuos varían aleatoriamente, el valor puede ser cercano a 2 (resultado ideal). Un valor p pequeño indica una tendencia no aleatoria en los residuos, para unos datos que corren sobre el tiempo. Es decir, un valor p por debajo de 0.05 (si se opera con un nivel de significancia del 95%) indica una posible autocorrelación serial [11]. Por lo tanto, se espera que el valor p sea mayor a 0,05.
3.2 Prueba de Kolmogorov-Smirnov (S)
La prueba de Kolmogórov-Smirnov es una prueba no paramétrica que determina la bondad de ajuste de dos distribuciones de probabilidad entre sí. En términos sencillos, con esta prueba se acepta o rechaza la idea de que los residuos provienen de una distribución normal. Cuando el valor p es mayor ó igual a 0,05, no se puede rechazar la idea de que los residuos provienen de una distribución normal con 95% de confianza [11].
En resumen, solo se analizan los modelos de crecimiento exponencial que cumplan las siguientes condiciones: 0.8 ≤ R2 ≤ 1; una relación estadísticamente significantes entre Y y, X; un valor p brindado por la prueba de bondad de ajuste Kolmogorov-Smirnov mayor a 0,05; un valor p brindado por el estadístico de Durbin-Watson mayor a 0,05.
4 Resultados y discusiones
En la Figura 2 se muestran los casos diarios por Covid-19 reportados en Colombia desde la aparición del primer caso hasta culminar el mes de octubre de 2020. En ella, además, se indica la ubicación de cada periodo de crecimiento exponencial (rectagulos rojos) durante la primera ola epidemiológica.
Observe que entre los meses mayo y junio existen dos periodos de crecimiento exponencial que se traslapan, esto sucede por conveniencia de ajuste, ya que de la manera en que están presentados, los periodos tienen un mejor coeficiente de determinación. La Figura 1 resalta el hecho de que en Colombia se logran identificar 10 periodo de crecimiento exponencial en la primera ola epidemiológica.
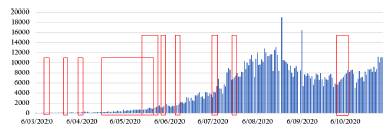
Figura 1 Periodos de crecimiento exponencial de los casos diarios reportados durante la primera ola epidemiológica en Colombia.
El país pasó por un periodo de crecimiento de 134 días (Figura 2). Sin embargo, el modelo exponencial no es el adecuado para ajustar este periodo, lo que evidencia el hecho, de que un R2 alto, no significa que el modelo sea el mas adecuado. La razón por la cual este modelo no puede ser validado, es el valor p del estadístico de Durbin-Watson y el de la prueba de bondad ajuste Kolmogorov-Smirnov, ya que son menores a 0,05 (Tabla 1), lo que sugiere la existencia de una posible correlación serial con un nivel de confianza del 95,0% (Figura 3).
De ahora en adelante se presentan periodos de crecimiento exponencial validados, es decir, que cumplen con todos los requisitos que se mencionaron con anterioridad. Los primeros tres periodos, cuentan con tasas de crecimiento altas, evidenciando el impacto de virus en la etapa temprana de propagación, cuando las medias sanitarias y de aislamiento no son lo suficientemente rigurosas. La Figura 4 muestra el primer periodo de crecimiento exponencial, entre el 13 y el 16 de abril de 2020, para este período, los datos se ajustaron mediante la regresión y1 = exp(-26,7592 + 0,5535x1) con un coeficiente de determinación R2 = 0,9710. En consecuencia, la tasa de crecimiento es k1 = 0,5535, lo que implica que por cada 10 personas que se expusieron al virus aproximadamente 5 fueron contagiadas.
En este periodo de cuatro días, se puede resaltar lo determinante de la migración en la propagación del virus, con 33 casos importados (Tabla 2), representando el 68,75% de los casos totales durante el periodo.
En este caso, se logran identificar 88 casos importados de Covid-19 (Tabla 3). La Figura 5 muestra que el segundo periodo se presenta entre el 26 y el 29 de abril de 2020. En este caso, los datos se ajustan a la regresión exponencial y2 = exp(-27,9046 + 0,4859x2) con un R2 = 0,9400. En consecuencia, la tasa de crecimiento es k2 = 0,4859 lo que implica que por cada 10 personas aproximadamente 4 personas se infectaron.
El siguiente periodo (Figura 6) se encuentra a tan solo 10 días del anterior, exactamente entre el 5 y el 8 de mayo de 2020, con una tasa de crecimiento (k3 = 0, 4491) superior al 40% . El ajuste a la regresión exponencial y3 = exp(-28,9501 + 0,4491x3) es de R2 = 0,9453. En este periodo los casos importados por Covid-19 aumentan a 95 (Tabla 4), lo que sugiere, que la migración fue un factor fundamental en la propagación del virus al inicio de la ola epidemiológica.
Ante el continuo incremento de casos, en Bogotá D.C en conjunto con otras ciudades decidieron realizar un simulacro de cuarentena obligatoria del 20 al 23 de marzo. Las medidas de aislamiento fueron efectivas, pero no suficientes para controlar la propagación, razón por la cual se establece aislamiento preventivo obligatorio, a partir del 24 de marzo [12].
Debido a los casos importados, Colombia solicita apoyo internacional para enfrentar la coyuntura de inmigrantes provenientes de Venezuela [13]. De ahí en adelante se observa que las tasas de crecimiento exponencial son mas bajas, de la misma forma, los casos importados por Covid-19 disminuyen, lo cual demuestra la efectividad del confinamiento y las medidas de prevención. Por otro lado, a partir del 9 hasta el 12 de abril se celebró semana santa, lo que significó reuniones familiares y circulación de la población a sitios de descanso, a pesar de las medidas implementadas por el estado. Además, la flexibilidad de la medida de confinamiento del 28 de abril permitió a algunos sectores de la economía reactivar sus labores dejando un saldo de aglomeraciones en ciudades como Bogotá y Barranquilla, sobre todo en el sistema de transporte publico, que encendieron las alarmas ente posibles aumentos en los contagios [14].
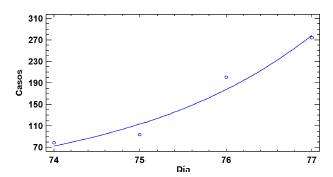
El incremento continuo de casos generados en semana santa aunado con la reactivación económica, generaron un periodo de crecimiento exponencial con un rango de 37 días, específicamente del 21 de abril al 27 de mayo de 2020 (Figura 7). El cual tiene un ajuste a la regresión exponencial y4 = exp( 1, 2945 + 0,0452x4) de R2 = 0,8815, y una tasa de crecimiento k4 = 0,0452.
Como se mencionó anteriormente el 28 de abril las empresas del sector manufacturero y de la construcción (más de 4.000 empresas), retornan a sus actividades, bajo protocolos obligatorios impuestos por el estado [15]. De esta manera, se observa el impacto de infección por Covid-19 en el regreso de algunas actividades laborales en el periodo anterior, especialmente en el de crecimiento exponencial identificado del 19 al 30 de mayo de 2020, tal y como se muestra en la gráfica de la Figura 8. Este se caracteriza por tener un ajuste a la regresión exponencial y5 = exp(-2,1247 + 0, 0728x5) de R2 = 0, 8563. Además, la tasa de crecimiento en este periodo es k5 = 0,0728, lo que evidencia un aumento en comparación con el periodo anterior.
Para los siguientes periodos las tasas de crecimiento sobrepasan el 10%, lo cual resulta alarmante, ya que el país ha venido con un aumento casi constante de los casos diarios reportados por Covid-19.
El 10 de mayo de 2020 en Colombia se celebró el día de las madres, lo que lo suscitó en una gran cantidad de contagios. Para el 11 de mayo la Policía Metropolitana atendió 608 fiestas por alteración de la tranquilidad e impuso 762 comparendos por incumplimiento a las medidas de aislamiento, toque de queda y ley seca [16] . Dicha celebración junto a la flexibilidad del aislamiento, revela un periodo de crecimiento exponencial entre el 1 y 4 de junio de 2020 (Figura 9). En la regresión exponencial y6 = exp(-12,8829 + 0,1520x6) los datos se ajustaron con R2 = 0, 9937. La tasa de crecimiento en este periodo es k6 = 0,1520, es decir, de cada 1000 personas expuestas al virus, al menos 150 resultaron contagiadas.
La migración nuevamente resultó un factor de preocupación, ya que además del incremento de los casos reportados, genera sesgos y por ende varios casos fueron reportados con retraso o incluso jamás se lograron identificar. En la Tabla 7 se observa que los casos importados disminuyo a 13; sin embargo, el 15 de mayo de 2020, durante el programa Prevención y Acción con el presidente, el ministro de Salud y Protección Social, anuncio la reunión con el gobierno de Brasil con el objetivo de establecer un plan de acción en la zona fronteriza frente a la pandemia de Covid-19, y que les permitiera a los dos países actuar de manera integral sobre los efectos de la pandemia en el Amazonas que había reportado 1003 casos hasta la fecha.
De esta manera los acontecimientos anteriormente mencionados generaron un periodo de crecimiento exponencial del 11 al 14 de junio (Figura 10). En este periodo los datos se ajustaron a la regresión exponencial y7 = exp(-9,8509 + 0,1217x7) con un R2 = 0, 9788. En consecuencia la tasa crecimiento es k7 = 0,1217, es decir, que de 1000 personas expuestas al virus al menos 100 fueron contagiadas.
En la Figura 11 se aprecia que desde el registro del primer paciente contagiado por Covid-19, el 6 de marzo 2020, el número de pruebas PCR aumento significativamente, alcanzando en el mes de julio el pico de muestras totales y pruebas positivas. Para el mes de octubre estas presentan una disminución; en este sentido los casos positivos guardan la misma relación que las muestras totales [19].

Figura 11 Gráfica realizada con datos obtenidos del Instituto Nacional de Salud. En ella se observa las muestras (curva superior) realizadas comparada con las pruebas que resultaron positivas (curva inferior) diariamente.
El día 19 de junio en Colombia se realizó el primer día sin IVA, lo que ocasionó aglomeraciones en los principales centros comerciales de cada ciudad, esta interacción social generó un nuevo periodo de crecimiento exponencial, con un rango de cinco días, con una tasa de crecimiento k8 = 0,1763. La gráfica de la Figura 12 muestra dicho periodo, en el cual, los datos se ajustan a la regresión exponencial y8 = exp(-21,1853 + 0,1763x8) con un R2 = 0,9360. Cabe destacar, que no todos los contagios se dieron el 19 de junio, sin embargo, en este día se desató una gran cantidad de contagios que impulsaron la propagaron el virus, sobrepasando, nuevamente, cifras de meses anteriores respecto a los casos diarios por Covid-19.
Por otra parte, el estado presentó nuevas flexibilizaciones de las medidas, tales como la salida a parques de niñas, niños y adolescentes a partir del 1 de junio en el periodo de aislamiento inteligente [20]. Sin embargo, el Gobierno Nacional extendió la emergencia sanitaria hasta el 31 de agosto, y entre las medidas se determinó la ampliación del aislamiento preventivo en personas mayores de 70 años, con ciertas salida a la calle bajo condiciones definidas [21]. Además, se autorizó la apertura gradual de centros comerciales en todo el país siempre y cuando cumplan con los protocolos de bioseguridad obligatorios [22]. Adicionalmente, en el mes de junio hubo tres lunes festivos.
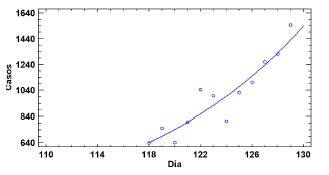
Teniendo en cuanta los factores hasta el momento mencionados y el incremento de casos diarios reportados por Covid-19, se puede identificar entre el 20 y 23 de julio un periodo de crecimiento exponencial (Figura 13). En este periodo, el ajuste de la regresión exponencial y9 = exp(-1,0698 +0, 0549x9) es de R2 = 0, 9862. Ademas, se puede evidenciar una disminución en la tasa de crecimiento k9 = 0,0549.
A principios de agosto hubo un aumento de los casos diarios por Covid-19, sin embargo, después de cinco meses no se logró identificar un periodo de crecimiento exponencial, incluso a partir del 29 de agosto de 2020 empiezan a decrecer hasta finales de septiembre. Razón por la cual, nuevos sectores empiezan a reabrir como es el caso de la reactivación del transporte aéreo [23]. De la misma forma, se toma la decisión de hacer la reapertura de ocho parques naturales [24]. El Ministerio de Salud y Protección Social entregó nuevos parámetros de bioseguridad para la prevención de la transmisión del Covid-19 en salas de cine, teatros, autocines y auto eventos, además, Centros de estética y cosmetología cuentan con protocolo de bioseguridad [25].
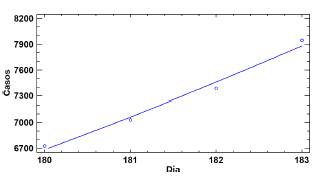
Adicionalmente, en el mes de septiembre empiezan a organizarse diferentes manifestaciones, por el descontento con el gobierno y abuso de autoridad por parte de la policía nacional; esto impulso a miles de personas a movilizarse por las principales ciudades generando aglomeraciones e incumpliendo con las medidas de aislamiento [26]. Dichos factores se relacionan con el último periodo de crecimiento exponencial en la primera ola epidemiológica del país. La gráfica de la Figura 14, muestra dicho periodo con un rango de 9 días, donde, los datos se ajustan a la regresión exponencial y10 = exp(-4,5063 + 0,0521x10) con R2 = 0,9859, dejando una tasa de crecimiento k10 = 0,0521.
En gráfica de la Figura 15, se presenta la positividad de las pruebas PCR en el transcurso de la primera ola, las franjas horizontales corresponden a las tasas de los crecimientos exponenciales estimados. En ella se observa que al inicio la positividad es menor a la tasa de crecimiento, pero a medida que transcurre el tiempo y las muestras aumentan, los papeles se invierten. Al inicio de la pandemia, la cantidad de pruebas realizadas no era significativa comparada con la dinámica de la propagación del virus, resulta evidente que las tasas de crecimiento sobrepasen la positividad. Al aumentar el tamaño de las muestras incrementó la positividad; no obstante, debido a las estrategias implementadas por el gobierno para mitigar los contagios [27], los periodos de crecimiento exponencial fueron menos frecuentes, mas cortos y con tasas de crecimiento mas pequeñas.
5 Conclusiones
La tasa de crecimiento más alta fue k1 = 0,5535 y corresponde al primer periodo de crecimiento exponencial, donde las medidas de prevención no eran estrictas (Gráfica 4). En contraste, la tasa de crecimiento más baja es de k10 = 0,0521, y pertenece al último periodo de crecimiento exponencial en la primera ola epidemiológica. Además, el primer periodo se caracteriza por su rango de 4 días, mientras el ultimo cuenta con un rango de 9 días. No obstante, no se puede concluir que a mayor rango menor tasa de crecimiento y esto queda evidenciado en el periodo más grande de crecimiento exponencial del 21 de mayo al 27 de junio, es decir un rango de 37 días.
Los principales factores que incidieron en el aumento de casos y por ende a un crecimiento exponencial, fueron la flexibilización de aislamiento obligatorio a preventivo [28], y la falta de acatamiento de las medidas preventivas, ya que aproximadamente el 25% de las personas que resultan positivas probablemente no realizarían la cuarentena [19]. La celebración de semana santa, del día de la madre y las actividades durante los días festivos generaron nuevos contagios que conllevaron a un crecimiento exponencial. El día sin IVA generó aglomeraciones que terminaron por aumentar los casos diarios. Por otra parte, hubo factores inevitables como la migración y el retorno obligatorio al trabajo de miles de ciudadanos para los cuales no les fue posible el teletrabajo.
El pico de positividad se alcanzó el 20 de julio de 2020, sin embargo, no se relacionó con ningún periodo de crecimiento exponencial. Además, no se encuentran fundamentos para establecer una relación de crecimiento directa entre la positividad y el crecimiento exponencial. De hecho, paso todo lo contrario, a medida que la positividad aumentaba los periodos de crecimiento exponencial eran menos frecuentes (Figura 15).
El total de casos reportados por Covid-19 hasta el 31 de octubre fue de 1.074.184, y los casos reportados diariamente en los periodos de crecimiento exponencial fue de 160.888, lo que corresponde al 14.9% de los casos reportados en la primera ola epidemiológica. Por otra parte, la tasa de crecimiento exponencial promedio es k = 0,2164. Los periodos de crecimiento exponencial fueron decisivos en la posición de Colombia, con respecto a los casos de Covid-19 a nivel mundial, como se sabe, Colombia es uno de los países con más número de contagios en el mundo, ocupando hasta finales de octubre el sexto puesto de los países con más infectados por Covid-19.
Por lo tanto, no resulta extraño encontrar periodos de crecimiento exponencial durante la primera ola epidemiológica en Colombia