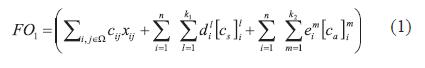Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Desarrollo
Print version ISSN 0122-3461On-line version ISSN 2145-9371
Ing. Desarro. no.28 Barranquilla July/Dec. 2010
ARTÍCULO CIENTÍFICO / RESEARCH ARTICLE
Optimización de redes de comunicación
por cable, un enfoque multiobjetivo
Combinatorial optimization for cable
communication network design, a
multi objective approach
Luís Fernando Galindres G*, Antonio H. Escobar Z**, Ramón A. Gallego Rendón R.***
Universidad Tecnológica de Pereira (Colombia)
* Ingeniero de Sistemas, M. Sc. (c) Universidad Tecnológica de Pereira. Pereira, Colombia. lugal@utp.edu.co
** Ingeniero Electricista, Ph. D. Profesor de la Universidad Tecnológica de Pereira. escobar@utp.edu.co
*** Ingeniero Electricista, Ph. D. Profesor de la Universidad Tecnológica de Pereira. ragr@utp.edu.co
Correspondencia: Universidad Tecnológica de Pereira, vereda la Julita, Pereira (Colombia). Tel.: 313-7122, Ext. 105.
Fecha de recepción: 23 de noviembre de 2009
Fecha de aceptación: 8 de octubre de 2010
Resumen
Este artículo resuelve el problema de la optimización de redes de comunicaciones por cable usando optimización multiobjetivo. El método usado en la solución del modelo matemático es un algoritmo especializado basado en el método Non-Dominated Sorting Genetic Algorithm (NSGA II). El modelo matemático planteado utiliza dos funciones objetivo: el costo de inversión y un indicador relacionado con la operación de la red. En la solución del problema son obtenidos frentes dominantes que proporcionan información al diseñador de la red acerca de cómo debe ser la configuración de mínimo costo y que cumpla con los requerimientos mínimos de señal en los nodos de conexión de los usuarios. Para esto se usa un sistema de prueba de la vida real.
Palabras clave: algoritmos evolutivos, optimización combinatorial, optimización multiobjetivo, redes de comunicación por cable.
Abstract
This paper solves the optimization problem of communication networks by cable using a multi objective algorithm. The mathematical model is solved using a methodology based on the Non-dominated Sorting Algorithm (NSGAII). The mathematical model uses two objective functions, one is the investment costs and the other is an indicator related to the network operation. The problem solution is a Pareto front that consider information about the network design, showing a set of network configuration with minimum cost and minimum requirements of signal levels in the costumer connection nodes. For that, a real life test system is used.
Key words: Cable communication Network, Combinatorial Optimization, Evolutive Algorithms, Multiobjective Optimization, Optimization Methods. Propylene.
1. INTRODUCCIÓN
El diseño de redes de comunicación por cable está asociado a la solución de un problema de optimización a través del cual se busca determinar la topología radial óptima de la red, con uno o varios objetivos definidos. Encontrar la topología óptima requiere evaluar implícita y/o explícitamente todas las topologías radiales posibles del sistema. Una forma de caracterizar el problema consiste en encontrar un árbol del grafo asociado a la red, que minimice la inversión, y el sobrante dé señal en los nodos y/o maximice la confiabilidad y que, además, satisfaga restricciones de operación como, por ejemplo, las asociadas a nivel de señal, capacidad de los circuitos y relaciones físicas que debe satisfacer la señal. Dado que la solución del problema debe ser un árbol del grafo, por causa de la exigencia de radialidad la configuración final contendrá solo aquellos caminos de conexión candidatos que permitan satisfacer todas las condiciones del problema al tiempo que representan la alternativa de más bajo costo de inversión. En este trabajo se explora la posibilidad de determinar un conjunto de soluciones usando un enfoque multiobjetivo, que garantiza que la señal se encuentra dentro de los niveles permitidos, al mismo tiempo que minimiza el nivel de señal sobrante en los nodos, respecto al nivel mínimo exigido.
El modelo matemático asociado al problema de optimización resultante hace parte de la categoría de problemas de programación no lineal enteros-mixtos (PNLEM), que se caracterizan por ser no lineales, poseer variables enteras y continuas, y en los cuales aparece el denominado fenómeno de "explosión combinatorial" [1] cuando aumenta el tamaño del sistema. Para un número grande de alternativas resulta prohibitiva su solución a través de técnicas de optimización exactas, porque en estos casos se convierte en un problema NP-completo, es decir, un problema que no puede resolverse en tiempos de cómputo polinomiales. La exigencia de radialidad es un factor adicional en el proceso de solución del problema. Para un número grande de alternativas y de nodos se requiere el uso de técnicas metaheurísticas para encontrar soluciones subóptimas de buena calidad. Debe tenerse en cuenta que las técnicas metaheurísticas no garantizan la solución óptima global, aunque eventualmente pueden encontrarla, según el tipo de problema analizado.
Tradicionalmente, el problema de redes de comunicación por cable se ha resuelto usando técnicas de optimización monoobjetivo, donde el único objetivo es la minimización de los costos de inversión [2], [3]. Por otro lado, el problema de optimización de la red de comunicaciones de la vida real es un problema que busca la maximización o minimización simultánea de varios objetivos, por lo que se constituye en un problema multiobjetivo [4], donde generalmente los objetivos se encuentran en conflicto. Dentro de los objetivos más comunes se encuentran: minimizar el costo de inversión, maximizar aspectos relacionados con la calidad de la señal y maximizar la confiabilidad del sistema. La optimización multiobjetivo es adecuada para resolver problemas con objetivos en conflicto, como cuando se desea simultáneamente minimizar el costo de inversión y maximizar la confiabilidad del sistema, ya que mejorar la confiabilidad implica una mayor inversión y reducir la inversión está asociada a una menor confiabilidad. Algo similar ocurre entre el costo de inversión y la calidad de la señal, ya que una topología de bajo costo, que conecte a todos los nodos, operará cerca de sus mínimos operativos, suministrando a los usuarios señales suficientes pero cerca al límite inferior. De otro lado, una señal de alta calidad en todos los nodos estará asociada a un mayor nivel de inversión.
En este trabajo se implementa una solución basada en el algoritmo multiobjetivo denominado NSGA-II (Non-Dominated Sorting Genetic Algorithm II). Una descripción detallada de este algoritmo puede ser encontrada en la referencia [5]. Como sistemas de prueba se utilizan los escenarios reportados en la referencia [2].
2. FORMULACIÓN MATEMÁTICA DEL PROBLEMA
Se plantean dos objetivos: el primero hace referencia a costos de inversión y el segundo, al nivel de señal sobrante en los nodos respecto al nivel mínimo exigido. Al incluir este nivel de señal excedente en el problema de optimización se direcciona el proceso de búsqueda hacia regiones donde se minimiza este excedente y en que pueden existir soluciones de menor costo de inversión.
Función objetivo asociada al costo de inversión: este objetivo busca determinar la cantidad mínima de cable coaxial y de elementos para división de señal (acopladores direccionales y divisores de señal) que permitan conectar todos los nodos de la red a un punto donde se encuentra disponible la señal, cumpliendo con el requerimiento de radialidad. Esta función objetivo será denominada FO1, y su formulación matemática es la siguiente:
Donde xij es una variable binaria que define si existe o no conexión entre los nodos i-j a través de cable coaxial, cij costo del cable coaxial entre los nodos i-j, dil es una variable binaria que define si existe o no un divisor del tipo l, [cs]il es el costo del divisor del tipo l localizado en el nodo i, eim es una variable binaria que define si existe o no un acoplador de señal del tipo m localizado en el nodo i, [ca]im es el costo del acoplador de señal del tipo m localizado en el nodo i. Para cada problema se deben definir los tipos de divisores y acopladores que se van a considerar así como también sus costos y sus características operativas. Finalmente, n es el número de nodos del sistema y W es el conjunto de caminos candidatos donde se pueden hacer conexiones usando cable coaxial.Función objetivo asociada a nivel de señal: este objetivo determina la diferencia entre el nivel de señal existente en la entrada de los amplificadores y el nivel de señal mínimo permitido. El nivel de señal se calcula considerando los diferentes parámetros de diseño de redes de banda ancha que lleva en cuenta la atenuación en los tramos y el efecto de los divisores y acopladores sobre el nivel de señal. El flujo de señal se basa en un método de barrido que parte del nodo fuente hasta llegar a los nodos finales, ver referencia [7]. Se determina la cantidad de señal a la entrada de cada amplificador (nodo) y se minimiza la diferencia entre el nivel de señal existente y el nivel mínimo permitido. Esta función objetivo denominada FO2, es formulada como la minimización de la señal sobrante, en decibeles, respecto al mínimo requerido. La función matemática que resulta de plantear este objetivo es la siguiente:
Donde ri corresponde a la cantidad de señal (en decibeles) que existe en el nodo i, por encima del nivel de señal mínimo requerido en dicho nodo. FO2 es el valor acumulado de señal sobrante en los n nodos del sistema.
Modelo de optimización propuesto: en la optimización multiobjetivo se procesan las funciones objetivo directamente con sus respectivas unidades y no son necesarios los parámetros de conversión y unificación de unidades ni los factores de peso que son necesarios en la optimización monoobjetivo cuando se intenta combinar varios objetivos en una única función. Otra característica de la optimización multiobjetivo es que, a diferencia de la optimización monoobjetivo, no existe una única solución que minimice y maximice simultáneamente todos los objetivos si se trata de analizar los que están en conflicto. En este artículo, la inclusión del segundo objetivo tiene como propósito direccionar el proceso de búsqueda hacia regiones de mejor calidad en cuanto involucra un factor que no está siendo evaluado explícitamente en la optimización monoobjetivo. A través de la optimización multiobjetivo se determina un conjunto de soluciones no dominadas con respecto a cualquier otra alternativa del conjunto de solución. Estas soluciones son definidas en el contexto de la optimización multiobjetivo como soluciones no dominadas o soluciones Pareto-óptimas. La selección de una solución particular de este conjunto depende de las características del problema y es tomada por un decisor [6] con base en criterios técnicos, económicos o subjetivos. En la práctica, en problemas tipo NP-completos se recurre al uso de técnicas metaheurísticas multiobjetivo para generar el conjunto de soluciones Pareto-óptimas, o un conjunto de soluciones cercanas a las soluciones Pareto-óptimas.
Un problema de optimización multiobjetivo consiste en encontrar un vector de variables de decisión (solución) que satisface un conjunto de restricciones de igualdad y/o desigualdad, y optimiza una función vectorial cuyos elementos representan las funciones objetivo. Estas funciones corresponden a los criterios de optimalidad, usualmente en conflicto. El problema multiobjetivo de optimización de redes de comunicación por cable que se analiza en este trabajo se define matemáticamente de la siguiente forma:
Para el problema anterior, (5) representa la restricción del número máximo de divisores permitidos por nodo. En es caso solo se considera la posibilidad de colocar un divisor por nodo.
En forma similar, (6) representa la restricción del número máximo de acopladores permitidos por nodo. En este caso solo se considera la posibilidad de colocar un acoplador por nodo. En un mismo nodo puede existir un divisor y un acoplador. k1 y k2 representan los tipos de divisor y acoplador definidos antes de resolver el problema.
La restricción (7) se refiere a que cada configuración debe ser radial; no deben existir lazos ni tampoco deben existir nodos sin conectar, lo que se logra definiendo F caminos o trayectorias. El concepto anterior se amplía en [7].
La restricción (8) corresponde a n-1 ecuaciones que describen el problema de flujo de señal. La restricción (9) corresponde a n inecuaciones de la forma (dbi ≥ 0), cantidad de decibeles en el nodo i.
En la restricción (10), fmin representa la frecuencia mínima de operación, fmax representa la frecuencia máxima de operación), foper representa la frecuencia de trabajo, la restricción (11) muestra que en el nodo i debe existir una cantidad mínima de señal con la que se garantiza su calidad.
En la restricción (12), ri representa el sobrante de señal en el nodo i.
3. CODIFICACIÓN E IMPLEMENTACIÓN DEL MÉTODO DE SOLUCIÓN
En la representación de una solución candidata se utiliza codificación binaria. Los nodos representan el punto de entrada a cada amplificador o a un elemento de división de señal, las ramas representan el trayecto entre dos nodos. Cada solución se identifica por un arreglo de unos y ceros, donde uno (1) en la posición i del arreglo significa que la rama i está conectada y hace parte del árbol; por el contrario, (0) en la misma posición significa que la i-ésima rama está desconectada. La figura 1 muestra un sistema típico de 8 nodos y 10 ramas. El vector que se presenta a continuación representa una propuesta topológica para el sistema mostrado en la figura 1 y es el siguiente: [ 1 1 1 1 0 1 1 0 1 0 ]
El flujo de señal y el estado de las señales se evalúa usando un algoritmo de flujo de señal. La población inicial tiene en cuenta la condición de radialidad y se genera mediante un algoritmo aleatorio. La descripción completa de este algoritmo puede ser observada en [8]. El algoritmo NSGA-II se fundamenta en el tradicional método de algoritmos genéticos así como en el concepto de dominancia y elitismo. Una visión más detallada de estos aspectos puede ser observada en [9].
Para la recombinación se implementó una forma especializada que se denomina tipo II y descrita en [7]. Con lo anterior se garantiza radialidad de las configuraciones candidatas (individuos). Finalmente, la mutación utiliza una estrategia conservando la radialidad de las configuraciones tal como es propuesta en [7], [8].
4. TÉCNICA DE SOLUCIÓN
La optimización multiobjetivo está asociada a un alto costo computacional, en el caso de problemas NP-completos, por lo que la utilización de las denominadas técnicas exactas se hace compleja sobre todo cuando el espacio de soluciones crece [10]. Por lo anterior se plantean las soluciones heurísticas estocásticas que alcanzan buenas soluciones en tiempos de computación razonables, en las que se incluyen los algoritmos evolutivos (AE). Una extensión de estos algoritmos surge como una excelente alternativa para la solución de los problemas multiobjetivo, y se les denomina MOEAs. En este trabajo se utiliza el algoritmo NSGA-II.
La optimización multiobjetivo deberá cumplir dos características que son esenciales para su buen desempeño: la primera, obtener un frente aproximado al frente Pareto-óptimo al final del proceso y, la segunda, mantener la diversidad de la población en el espacio objetivo durante el proceso [11].
El algoritmo NSGA-II muestra un buen comportamiento con respecto a estas dos características: presenta un frente de Pareto de muy alta calidad, que se distribuye adecuadamente en el espacio de solución de las funciones objetivo [12]. La solución en la optimización multiobjetivo se presenta como el mejor conjunto de soluciones xi no dominadas, lo que se denomina frente óptimo de Pareto FP* como se describe en [13].
El algoritmo NSGA-II (Non-Dominated Sorted Genetic Algorithm versión II) fue mostrado por Deb como una versión mejorada del algoritmo NSGA presentado por Srinivas y Deb [9].
5. PRUEBAS Y RESULTADOS
Para verificar el desempeño del algoritmo NSGA II se utilizó un sistema real correspondiente a la ciudad de Pereira (Colombia), cuyos datos aparecen en [7]. Los parámetros usados en el algoritmo fueron los siguientes:
La figura 2 muestra el frente de Pareto obtenido usando el algoritmo NSGA-II en las generaciones 50 y 200, respectivamente.
Una de las características del algoritmo NSGA II es permitir que en cada generación más individuos hagan parte del frente de Pareto. En la generación 1000 hacen parte del frente 145 de los 200 individuos de la población. En la figura 3 se muestra el frente de Pareto para la generación 1000 y el frente de Pareto final que se obtiene en la generación 1160.
La metodología propuesta establece un conjunto de soluciones de calidad con información, que incluye el costo de la solución y la calidad de la señal, a fin de que el diseñador de este tipo de redes tome la mejor decisión.
En la optimización multiobjetivo se utilizan diferentes métricas que miden la calidad del frente obtenido, y que se clasifican según varias características:
- ¿Qué tan cerca está el frente obtenido con respecto al óptimo global (supone que se conoce el óptimo global)?
- ¿Cómo es la distribución de las soluciones en todo el frente?
- Métricas que combinan los dos factores anteriores.
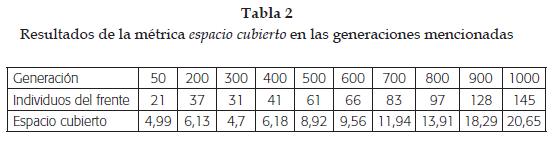
En este artículo se utiliza la métrica correspondiente al segundo punto, llamada espacio cubierto, que determina el tamaño del conjunto global en el espacio de las funciones objetivo. En las referencias [14] y [15] se encuentra información detallada sobre métricas en optimización multiobjetivo.
En la tabla 2 se muestra la variación de esta métrica a través de las diferentes generaciones.
En el problema propuesto se observa que en la medida en que se avanza en el número de generaciones, el frente se distribuye adecuadamente tal como se puede observar en las figuras 2 y 3. También se observa cómo el número de individuos de soluciones no dominadas se incrementan. El espacio cubierto se incrementó con el número de generaciones, lo que refleja una mayor cobertura en el espacio de solución.
6. CONCLUSIONES
Fue resuelto el problema de redes de comunicación por cable usando una técnica de optimización multiobjetivo denominada NSGA II. La implementación del multiobjetivo ofrece resultados que cumplen con los objetivos propuestos, es decir, mínima inversión y niveles adecuados de señal para los usuarios de la red.
La metodología propuesta es una herramienta de gran utilidad en el diseño de las redes de comunicación por cable, pues identifica configuraciones de mínimo costo con niveles de señal apropiados para el usuario.
Se encontró que el uso del algoritmo NSGA II cumple con los dos objetivos principales de una optimización multiobjetivo: encontrar un conjunto de soluciones de buena calidad y mantener la diversidad de la población tanto como sea posible. El algoritmo NSGA II permite hallar un amplio frente de Pareto final con muy buenas soluciones derivadas de los conjuntos de soluciones no dominadas y del factor de elitismo que posee este algoritmo.
La metodología propuesta presenta un comportamiento que puede ser considerado satisfactorio para el problema planteado, ya que se obtiene un frente con muchas soluciones, diversificadas y de calidad adecuada.
En este trabajo se propone una metodología con base en el algoritmo multiobjetivo NSGA II; en futuros desarrollos recomienda el estudio de otros objetivos como la disponibilidad del servicio la realización de análisis comparativos con otros algoritmos multiobjetivo.
Referencias
[1] R.A. Gallego, A.H. Escobar y E.M. Toro, Técnicas Metaheurísticas de Optimización. Pereira, Colombia: Universidad Tecnológica de Pereira, 2008, pp. 1-360. [ Links ]
[2] L.F. Galindres, R.A. Gallego y A.H. Escobar, "Técnica de optimización combinatorial aplicada al diseño de redes de comunicación por cable", Scientia Et Technica, n.° 39, pp. 332 - 337, 2008. [ Links ]
[3] H. Chou, G. Premkumar and Chao-HsienChu, "Genetic Algorithms for Communications Network Desing - An Empirical Study of the Factors that Influence Performance", IEEE Transaction on Evolutionary Computation, vol. 5 no.3, pp. 236-249, 2001. [ Links ]
[4] C. Coello. (2003). Evolutionary Multiobjective Optimization: Current and Future Challenges. [Online]. Disponible: http://delta.cs.cinvestav.mx/~ccoello/conferences/coello-wsc7.pdf.gz. [Acceso: Marzo 2009]. [ Links ]
[5] K. Deb, Multi-Objective Optimization using Evolutionary Algorithms, vol. I. Kanpur: Wiley, 2001, pp. 179-183. [ Links ]
[6] K. Miettinen, Nonlinear Multiobjective Optimization, vol. I. Jyvaskyla: Kluwer Academic Publishers, 1999, pp. 14-15. [ Links ]
[7] L.F. Galindres y E. Toro, "Optimización de redes de Comunicación utilizando Algoritmos Genéticos". Tesis de grado, Universidad Tecnológica de Pereira, 2003. [Online]. Disponible: http://www.utp.edu.co/~planeamiento/prod_aca/tesis/OPTIMIZACION_REDES_COMUNICACION_AG.pdf pp. 114-139 [Acceso: Marzo 2009]. [ Links ]
[8] J.C. Jaramillo, J.A. Orozco, R.A. Gallego and R.A. Romero, "Modified Genetic Algorithm for Network Reconfiguration in Distribution System", Memorias del IV Induscon 2000, Porto Alegre, Brasil, pp. 386 - 391, 2000. [ Links ]
[9] K. Deb, Multi-Objective Optimization using Evolutionary Algorithms, vol. I. Kanpur: Wiley, 2001, pp. 209-218. [ Links ]
[10] M.T. Jensen, "Reducing the run-time complexity of Multiobjective EAs: The NSGA-II and other algorithms", IEEE Transactions on Evolutionary Computation, vol. 7, pp. 503-515, 2003. [ Links ]
[11] M. Laumanns, L. Thiele, K. Deb and E. Zitzler. (2008, jun.). Combining Convergence and Diversity in Evolutionary Multi-Objective Optimization, [Online]. Disponible: ftp://ftp.tik.ee.ethz.ch/pub/people/laumanns/LTDZ2002b.pdf. [Acceso: Marzo, 2009] [ Links ]
[12] K. Miettinen, Nonlinear Multiobjective Optimization, vol. I. Jyvaskyla: Kluwer Academic Publishers, 1999, pp. 5-14. [ Links ]
[13] K. Deb, Multi-Objective Optimization using Evolutionary Algorithms, vol. I. Kanpur: Wiley, 2001, pp. 33-46. [ Links ]
[14] C. Coello. (2005, jul.). Introducción a la optimización multiobjetivo usando Metaheurísticas. [Online]. Disponible: http://elavio2005.uniandes.edu.co/MiniCursosTutoriales/Coello3.pdf [Acceso: Septiembre, 2009] [ Links ]
[15] C. Crosan (2003). Performance metrics for multiobjective optimization evolutionary algorithms. [Online]. Disponible: http://www.cs.ubbcluj.ro/~cgrosan/grosanCAIM.pdf [Acceso: Septiembre, 2009] [ Links ]