INTRODUCCIÓN
La alometría es el estudio del tamaño y sus consecuencias (Gould, 1966), es decir, las proporciones entre las medidas lineales de las plantas y las medidas de área o volumen obedecen a una regla que es la misma para todas las poblaciones que viven en las mismas condiciones. Dichas medidas morfométricas están relacionadas entre ellas, generando relaciones alométricas que hacen que el desarrollo de una se pueda expresar proporcionalmente con el desarrollo de otras partes del organismo (Mora-Delgado, 2018). Esta relación, se deriva del desarrollo ontogenético de los individuos, que es el mismo para todos, excepto la variabilidad asociada con la historia personal de cada uno; este es el principio básico de la alometría, que predice una medida de un atributo basado en otra medida (Picard et al. 2012). Esta relación expresa proporcionalidad entre los aumentos relativos de las medidas (Huxley, 1924; Gayon, 2000). En este orden, una ecuación alométrica es una fórmula que formaliza esta relación cuantitativamente.
Varios investigadores han hecho reportes sobre modelos alométricos para predecir biomasa aérea en especies leñosas, como los reportados por Segura & Andrade (2008) e Iglesias & Barchuk (2010); unos pocos están dedicados a formular ecuaciones para predecir biomasa forrajera de especies usadas en el trópico americano, entre ellos, los más relevantes, son los estudios con Morus alba (Armand, 1994), Acacia pennatula y Guazuma ulmifolia (López-Merlin et al. 2003) y Cercidium floridum Benth. Ex A. Gray, en el subtrópico mexicano (Guillén et al. 2007); sin embargo, solo se encontró un reporte específico con T. diverifolia, realizado en Cuba, en el cual, se hizo un seguimiento durante dos años para describir, mediante diferentes criterios estadísticos, el comportamiento de algunos componentes morfológicos de esta especie y determinar los modelos de crecimiento de mejor bondad de ajuste (Ruiz et al. 2012). El estudio concluye que la información obtenida sugiere un camino para investigaciones futuras, relacionadas con la producción de biomasa.
Tithonia diversifolia es una asterácea arbustiva utilizado como forraje para el ganado, sea en pastoreo o para corte y acarreo, por lo cual, la predicción de su desarrollo constituye un conocimiento práctico, para la toma de decisiones. Ciertas etapas del desarrollo de las especies animales y vegetales se han modelado exitosamente con ecuaciones exponenciales o lineales, que tienen la habilidad de imitar importantes procesos físicos, químicos o biológicos y describir cómo y porqué resulta una respuesta particular; la mayoría de los modelos de crecimiento de cultivos caen dentro de esta categoría de ecuaciones (Santiago-García, 2016; Gálvez et al. 2010). Así, el cálculo del crecimiento la biomasa producida por el arbusto representa una información útil para el planificador agropecuario. Tal cálculo podría ser estimado a partir de otras medidas lineales del arbusto, para poder predecir la producción de biomasa, sin tener que cosecharla. Algunas ecuaciones determinísticas han sido usadas para estimar biomasa y, a partir de ella, calcular el volumen de carbono capturado en un sistema forestal o para una especie específica (Riofrío et al. 2013).
Las mediciones de la altura de los arbustos relacionadas con el área de dosel, se pueden usar en la estimación del volumen de biomasa aérea, proveyendo así una herramienta práctica para describir la producción de biomasa de los arbustos. En este sentido, Thorne et al. (2002) evaluaron una técnica para estimar el volumen (V) del dosel de arbustos, usando la fórmula V = 2/3 π H (A/2 x B/2) (siendo H, la altura total del arbusto y, A y B, los diámetros mayor y menor de la elipse, que forma la proyección de la copa del arbusto), derivada de la fórmula básica del volumen elipsoidal. En la figura 1, se hace una interpretación gráfica de esta fórmula en una imagen de T. diversifolia, donde los diámetros se representan con D1 y D2 y la altura por H.
Antes, otros autores habían usado fórmulas matemáticamente equivalentes, para estimar volumen de dosel. Algunos de ellos, usaron la fórmula del volumen rectangular V = (H x W x L), siendo H, la altura; W, el ancho y L, el largo (Uresk et al. 1977) y también la de un cilindro elíptico (V = π (H) [eje mayor/2 x eje menor/2], siendo H, nuevamente la altura; esta fórmula fue usada para estimar volumen de dosel de diferentes especies de arbustos (Lyon, 1968; Peek, 1970; Wambolt et al. 1994); sin embargo, estas fórmulas suelen brindar grandes errores en el cálculo del volumen de dosel, porque presentan, usualmente, formas esféricas y elipsoidales, por lo tanto, la fórmula de volumen rectangular suele sobreestimar el volumen; en el mismo sentido, la forma cilíndrica elíptica no integra distancias radiales cambiantes a lo largo de los ejes verticales de las plantas (Thorne et al. 2002). Por otra parte, la fórmula de volumen cónico, V = (π r2 H) / 3, en la cual, r es el radio y H, la altura del arbusto (Bryant & Kothmann, 1979), puede subestimar el volumen de dosel. Predecir la biomasa con mecanismos no destructivos constituye una ayuda para los manejadores de fincas e investigadores agropecuarios y justifica esta investigación, dado el ahorro de tiempo y de recursos, en los procesos de investigación y productivos. Por lo anterior, el objetivo de este estudio fue producir una ecuación confiable para estimar la biomasa de las plantas de Tithonia diversifolia, de forma no destructiva, usando mediciones del dosel como variables independientes, para generar una ecuación alométrica, con el fin de proporcionar un método rápido, para estimar la biomasa forrajera.
MATERIALES Y MÉTODOS
El estudio, se llevó a cabo usando la base de datos de monitoreo de un cultivar de T. diversifolia, de la colección del programa de Hortalizas de la Universidad Nacional de Colombia, sede Palmira. La misma fue establecida en octubre de 2012, con materiales provenientes de 43 localidades del sur occidente de Colombia (Valle del Cauca, Caldas, Quindío, Risaralda y Tolima), mediante siembra de cangres de 60cm de largo cada uno, a una densidad de 1m de distancia entre sitios, 2m entre surcos y cinco sitios por cada introducción (10 plantas). Se hizo un corte de uniformización a los 4 meses, podando a 40cm todas las plantas. El área experimental tuvo una superficie de 880m2, en un diseño de surcos cada 2m y distancia entre plantas de 1m, para un total de 440 unidades experimentales. El cultivo estaba establecido en un lote de la finca experimental de la Universidad Nacional de Colombia -CEUNP-Palmira; 24°C, 1.000m s.n.m., precipitación anual 1.020mm y humedad relativa 72%, en el municipio de Palmira, Colombia; con una estación seca de julio a agosto, pertenece a la zona climática cálido-moderada de la formación Bosque Seco Tropical (BS-T), con predominio de suelos vertisoles (epiaquert ustico) (Acosta et al. 1997).
De noviembre a diciembre de 2013, se muestrearon 30 arbustos de T. diversifolia en etapa de pre-floración. Para ello, se hizo una cosecha de biomasa (hojas más tallos menores a 1cm de diámetro) cada 60 días, durante el periodo experimental. Para poder correlacionar las medidas lineales del dosel con el peso de la biomasa, se hicieron sucesivos cortes del forraje. Así, se tomó el promedio de todos los cortes manuales de la copa completa a 40cm del suelo, pesando, cada vez, con una balanza portátil digital, marca MC® China. Este procedimiento permitió obtener la biomasa fresca de cada planta, la cual, fue secada en una estufa de secado Binder® serie FD 53, a 120°C, por 24 horas, para obtener la biomasa de materia seca (MS).
Los componentes del volumen del dosel, se midieron tomando lecturas de la altura y de dos diámetros al 50% de la altura de T. diversifolia. La altura del dosel (m), se determinó midiendo desde el suelo hasta la rama más alta de material vegetal fotosintéticamente activo. Se tomó la medida del área del dosel, mediante dos diámetros del área de la copa, definida como la extensión más amplia de material vegetal fotosintéticamente activo, que intersecta un plano que pasa horizontalmente, a través de la planta, al 50% de la altura de la planta; se tomaron perpendicularmente en ángulo recto el uno al otro. Cada diámetro, se dividió entre dos para desarrollar la ecuación y estimar el área de una elipse, siendo AD = π (D1 / 2 x D2 / 2) [Ecu. 1], donde, D1 y D2 son los diámetros. El volumen del dosel (VolE), se estimó aplicando las mediciones de altura y 2 diámetros, a una modificación de la fórmula básica del volumen elipsoidal VolE = 2/3 π HD (D1/ 2 x D2 / 2) [Ecu. 2], donde, HD es la altura del dosel y, D1 yD2 son los dos diámetros perpendiculares.
A esta fórmula, se le realizó una modificación para ajustarla, con base en una estimación del valor de la densidad de dosel, con lo cual, se propone trabajar con la fórmula modificada: VolEA = DD (2/3 π HD (D1 / 2 x D2 / 2)) [Ecu. 3], donde, DD es densidad del dosel. Dicha densidad del dosel, se estimó cualitativamente, mediante la clasificación visual de la copa de los arbustos y mediante una calificación del grado de oclusión. Para eso, se estimó la densidad del dosel con una tarjeta de transparencia de follaje de USDA Forest Service (2010), así, DD se usó como factor de ponderación en la fórmula del volumen de dosel.
Las variables más correlacionadas con la biomasa fueron seleccionadas, utilizando coeficientes de correlación de Pearson (R). La producción de biomasa, se estimó mediante las ecuaciones de los modelos Lineal (ŷ = α + βX); Potencial (ŷ = αXβ); Polinómico (ŷ = -α+βX-γX2); Monomolecular (ŷ= α(1-β)-γX); donde, ŷ es la variable de respuesta y, α, β y γ, los parámetros a determinar, mediante el desarrollo de las anteriores ecuaciones. Los datos fueron corridos en el software Infostat (Di Rienzo et al. 2008). Estos modelos, se compararon en función de los valores de R y los estadísticos Bayesiano (BIC) y Akaike (AIC), siendo las ecuaciones con mejor ajuste aquellos que presentan menores valores en estos parámetros (Sakamoto et al. 1986). En sentido jerárquico, se consideró el menor valor del criterio de Akaike (AIC), el menor valor de raíz media del cuadrado del error (RMSE) y el mayor coeficiente de determinación (R2) (Riofrío et al. 2013).
RESULTADOS Y DISCUSIÓN
Las medidas lineales y sus derivados tienen una variación importante, comprensible en el caso de una colección de material genético de diferente origen. La variabilidad también se refleja en la dispersión de los valores expresados en los promedios, valores mínimos y máximos de los datos paramétricos, como se presenta en la tabla 1.
Tabla 1 Estadística descriptiva parámetros lineales morfométricos y sus combinaciones en Tithonia diversifolia.

DE: Desviación Estándar.
Las matrices de correlación (Tabla 2) indican que el volumen ajustado y la biomasa son los parámetros más interesantes para construir ecuaciones de regresión y de predicciones de la biomasa forrajera, dado el alto coeficiente de Pearson, que indica una alta asociación entre estas dos variables.
Tabla 2 Coeficiente de correlación de Pearson entre variables, medidas en plantas de Tithonia diversifolia.

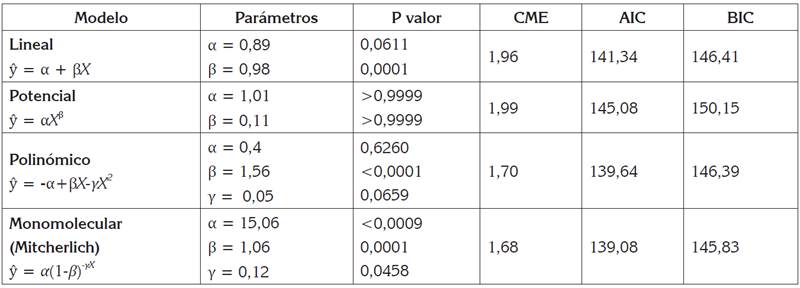
Una vez corridos los datos en ecuaciones de regresión no lineal y lineal, se encontró que los modelos polinómico y monomolecular tuvieron el mayor ajuste; sin embargo, entre estos dos, el modelo Ӯ = 15,06 (1-1,06) -0,12X es el que mejor predice la biomasa, dado que los estadísticos AIC y BIC sugieren que este es el que presenta mejor bondad de ajuste. Como se puede ver en la tabla 3, los modelos lineal y potencial fueron los que presentaron menor ajuste, aunque el R2 (0,80), sugiere una alta predecibilidad de la biomasa forrajera, mediante la medición del volumen estimado, a partir de la medición de la altura de dosel, dos diámetros perpendiculares y un factor de ajuste dado por la densidad de dosel.
Tabla 3 Ecuaciones y estimadores estadísticos derivados del análisis de regresión no lineal entre el volumen ajustado, para predecir la biomasa de dosel de Tithonia diversifolia.
En la figura 2, se representa la curva de regresión no lineal, en la cual, se puede observar los resultados de la modelación, donde se puede detallar que los valores estimados de biomasa están muy cerca de los valores observados. El coeficiente R2 indicó que las estimaciones tenían una precisión del 80%; es notoria una ligera disminución de la pendiente, a media que aumenta el volumen.
Si bien, hay varios reportes sobre modelos alométricos para predecir biomasa aérea, son escasos los estudios dedicados a formular ecuaciones para predecir biomasa forrajera. Aunque no se han reportado modelos específicos para predecir la producción de biomasa forrajera de T. diverifolia, en Cuba, se hizo un estudio durante dos años, en condiciones de secano, para describir, mediante diferentes criterios estadísticos, el comportamiento de algunos componentes morfológicos de esta especie y determinar los modelos de mejor bondad de ajuste; el estudio concluye, que la información obtenida abre un camino para investigaciones futuras, relacionadas con la producción de biomasa (Ruiz et al. 2012).
Este estudio reporta el comportamiento del peso total en 1m lineal de la planta, representado con mejor ajuste en un modelo ajustado (R2 = 0,83), que explicó el aumento de esta variable hasta las 18 semanas, con un incremento quincenal promedio fue de 216,38g.
En otras especies, se han reportado modelos alométricos para predecir el volumen y la biomasa y por extensión; estas ecuaciones constituyen la base para estimar carbono almacenado en agroforestales (Segura & Andrade, 2008). Así, Iglesias & Barchuk (2010) reportaron modelos de regresión para estimar la biomasa aérea total de seis especies arbustivas y arbóreas de la familia Fabaceae, nativas del Chaco Árido. Estos modelos incluyeron distintas combinaciones del diámetro a la base (DAB) y la altura de los individuos. Todos ellos predijeron aceptablemente la biomasa por especie, si bien el de regresión lineal que utiliza el DAB, como variable independiente, presentó el mejor ajuste.
Armand (1994) utilizó el volumen del dosel para estimar la biomasa de Chamaecyfisus proliferus, Gledifsia friacanthos, Medicago arborea, Robinia pseudoacacia y Morus alba, obteniendo una ecuación de alta predictibilidad (MSE = 0,64 (V0L)0,884), donde MSE es materia seca, con una buena correlación (R = 0,96). Esta ecuación sirvió, por muchos años, para generar medidas de biomasa, ya que se basa en parámetros fácilmente medibles y porque es un indicador rápido y confiable para estimar la fitomasa de las especies arbóreas (Etienne, 1989).
Por su parte, Guillén et al. (2007) obtuvieron ecuaciones de predicción de la producción de forraje de Cercidium floridum Benth. Ex A. Gray, en el desierto de Sonora (México), en mediciones durante dos años consecutivos; este estudio, se basó en la medición de altura de la planta, diámetro de tallo, diámetro mayor de la corona, diámetro menor de la corona y volumen. Como variables dependientes, se cuantificaron el peso seco de las hojas, peso seco de los tallos y peso seco total. Los modelos obtenidos fueron elegidos con base en los coeficientes de determinación (R2) más altos y al valor del error estándar (EE). La ecuación que mejor estimó el peso seco total estuvo mejor definida por las variables diámetro mayor de la corona, volumen y altura.
Por otra parte, mediciones de diámetro a altura de pecho (DAP) fueron suficientes para estimar la biomasa aérea de especies forrajeras, como Gliricidia sepium y Leucaena leucocephala. El estudio de Gómez-Castro et al. (2010) estima el almacenamiento de carbono de Gliricidia sepium y Leucaena leucocephala, a partir de la cuantificación de biomasa aérea (BA), fraccionada en biomasa de tallo, de ramas y de follaje; a su vez, las mediciones de diámetro a la altura del pecho (DAP), altura total del árbol y los pesos de tronco, ramas y follaje, se ajustaron a una serie de modelos exponenciales y logarítmicos, predictores de la biomasa aérea (BA). Para el caso de L. leucocephala, el modelo de mejor ajuste tuvo fue LN (BA) = -1,46+1,69 LN (DAP) y para G. sepium, el modelo BA = 3,27e0,075(DAP).
Esto contrasta con lo encontrado en nuestro estudio, en el cual, la biomasa aérea total seca fue determinada a partir de la medición del volumen de dosel, estimado mediante el producto de la altura del dosel por los dos diámetros, divididos entre dos y multiplicados por π.
En síntesis, se sabe que la tendencia es a buscar ecuaciones predictores específicas para las diferentes especies, por lo que este trabajo constituye un aporte de a la predicción de la biomasa de T. diversifolia. En este sentido, este estudio cumple con una función básica de la alometría, que radica en predecir una medida de un atributo basado en otra medida (Picard et al. 2012).
Este trabajo constituye un avance en el uso de una ecuación alométrica, basada en mediciones lineales, que permite facilitar la estimación de la biomasa de especies arbustivas, para evitar técnicas destructivas. Se demuestra la factibilidad de realizar estimaciones fiables de la biomasa de T. diversifolia con modelos que utilizan pocas variables de fácil medición, en este caso, el volumen de dosel estimado, mediante el producto de la altura del dosel, por los dos diámetros, divididos entre dos y multiplicados por π, al cual, se aplica un factor de ajuste determinado por la densidad de dosel, según fórmula para calcular área de un dosel elipsoide.
Dada la relación entre el volumen, la producción de biomasa y el almacenamiento de carbono, se recomienda realizar estudios adicionales de modelación de la capacidad de almacenamiento de carbono de esta especie, en los tejidos leñosos.
















