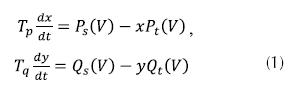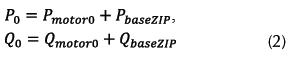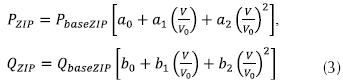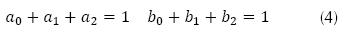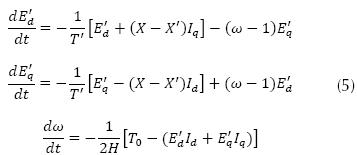DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a13

Obtención de modelos de carga compuestos en sistemas de potencia para análisis dinámico: revisión y aplicación

Composite load models in power systems for dynamical analysis: review and application

Sandra Milena Pérez Londoño*,
Luis Fernando Rodríguez García**,
Juan José Mora Flórez***

* Ingeniera electricista, magíster en Ingeniería Eléctrica, doctora en Ingeniería. Docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: saperez@utp.edu.co
** Ingeniero electricista, magíster en Ingeniería Eléctrica. Investigador de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: luferodriguez@utp.edu.co
*** Ingeniero electricista, magíster en Potencia Eléctrica, magíster en Tecnologías de la Información, doctor en Tecnologías de la Información; docente de la Universidad Tecnológica de Pereira. Pereira, Colombia. Contacto: jjmora@utp.edu.co

Fecha de recepción: 12 de marzo de 2014 Fecha de aceptación: 19 de enero de 2015

Citation / Para citar este artículo: Pérez Londoño, S. M., Rodríguez García, L. F., & Mora Flórez, J. J. (2015). Obtención de modelos de carga compuestos en sistemas de potencia para análisis dinámico: revisión y aplicación. Revista Tecnura, 19(44), 171-189. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a13

Resumen

En este artículo se presenta una revisión de las metodologías principales empleadas en la obtención de modelos de carga compuestos en sistemas eléctricos de potencia. Como estrategia de presentación de esta investigación, inicialmente se realiza la descripción y clasificación de las metodologías empleadas para obtener los modelos de carga compuestos, de sus diferentes modificaciones y de la utilización de nuevas herramientas durante los últimos años, de acuerdo con la información disponible en más de 60 referencias encontradas en las principales bases de datos. Las ventajas del modelo de carga compuesto se comprueban en la parte final del artículo, en donde se compara su comportamiento con el modelo de carga estático y se hace un análisis de la capacidad de generalización ante diferentes perturbaciones del sistema de potencia. Este trabajo sirve como una referencia útil en la discusión relacionada con aplicaciones del modelado de carga en los sistemas eléctricos de potencia.

Palabras clave: estimación de parámetros, modelado de carga, simulación de sistemas de potencia, sistemas eléctricos de potencia.

Abstract

This paper is oriented to present a review of different approaches commonly applied to obtain composite load models used in electric power system studies. As presentation strategy, there is initially a detailed description and classification of the methodologies used to obtain composite load models, their different modifications and the use of new tools during the last years, according to the available information from more than 60 references found in databases. The advantages of composite load model are evaluated and highlighted at the final part of this paper, where its behavior is compared to the static load model and an analysis of the generalization capability considering different power system disturbances is presented. This research work is a useful reference in the discussion associated to applications of load modeling in electric power systems.

Keywords: electric power systems, load modeling, parameter estimation, power system simulation.

Introducción

En los sistemas eléctricos de potencia el modelado de la carga representa un gran desafío, debido a su naturaleza compleja y variante en el tiempo, comparativamente con otros componentes como generadores o líneas de transmisión, para los cuales existen modelos ampliamente analizados y empleados satisfactoriamente.

En los últimos treinta años se ha realizado una considerable cantidad de investigaciones en el área del modelado de carga, incluyendo tres recomendaciones del grupo de trabajo en modelado de IEEE (IEEE Task Force on Load Representation for Dynamic Performances, 1993) (IEEE Task Force on Load Representation for Dynamic Performances, 1995a) (IEEE Task Force on Load Representation for Dynamic Performances, 1995b), además de muchos artículos en donde se han presentado diversas propuestas en cuanto a modelos matemáticos, enfoques y metodologías. Aun así, esta sigue siendo un área de constante y vigente investigación. Actualmente, la inclusión de nuevos tipos de cargas en los sistemas eléctricos de potencia (cargas electrónicas, generación distribuida, entre otras), también ha influido en que esta sea un área de creciente interés por parte de los investigadores, para definir modelos que se adapten a las características propias de este tipo de cargas (Department of Energy and Climate Change (DECC), 2010).

Para la definición de los modelos de carga se han considerado tanto las características de las cargas (estáticas o dinámicas), como las metodologías que se han empleado para su obtención (enfoque basado en componentes o en mediciones) (Kundur, 1993). Para el caso específico del modelado dinámico de carga, se han empleado los modelos de recuperación exponencial y el modelo compuesto, siendo este último uno de los más analizados, debido a que más de 60% de la potencia total demandada en los sistemas eléctricos de potencia corresponde a los motores y, por tanto, es razonable incluir su comportamiento dinámico en el modelo de la carga para estudios de estabilidad en sistemas eléctricos (Ornata & Uemura, 1998) (Ma, He, & Hill, 2006).

En el transcurso de los últimos años se han empleado diversas técnicas para el modelado de carga, desde metodologías que abordan la inteligencia artificial (Chen & Mohler, 2003) (Wang, Li, Su, & Xia, 2006) (Abdelaziz, Badr, & Younes, 2007) (Li, Wang, & Li, 2008), hasta metodologías de optimización (Wu, Wen, Nuttall, Shimmin, & Cheng, 2003) (Wen, Jiang, Wu, & Cheng, 2003) (Shi & He, 2003) (Knyazkin, Cañizares, & Söder, 2004) (Ju, y otros, 2007), que mejoran las propuestas clásicas empleadas en la implementación de los modelos. Sin embargo, del trabajo de revisión (Milanovic, Yamashita, Martinez, Djokie, & Korunovic, 2013), se observa cómo la utilización de los modelos de carga dinámicos es bastante baja, comparativamente con los modelos estáticos, a pesar de que su imposibilidad de reflejar las condiciones reales de la carga ya ha sido analizada y reportada en una gran cantidad de artículos (Mauricio & Semlyen, 1972).

Por otra parte, debido al auge de los sistemas de monitorización de área amplia (WAMS), la tendencia en el modelado de carga está encaminada a la incorporación de la información recopilada por estos sistemas para el desarrollo y perfeccionamiento de los modelos de carga en los sistemas eléctricos. La disponibilidad de estas mediciones en los sistemas eléctricos de potencia permite monitorizar permanentemente el comportamiento de las cargas ante los eventos que ocurren en la operación del sistema. Sin embargo, estas mediciones también se pueden utilizar para propósitos de sintonización de modelos de carga, empleando metodologías de estimación. En la representación de la carga para propósitos de análisis dinámico, los modelos compuestos siguen siendo ampliamente aplicados y aceptados, dado que sus resultados presentan mejor precisión en comparación con otros modelos de carga, como los modelos con ecuaciones de diferencia (Shi, Peng, & Liu, 2012).

Ante este panorama, es importante contar con un análisis completo de la bibliografía disponible, que recoja información sobre el estado del arte de las diferentes metodologías empleadas en la obtención de modelos de carga dinámicos, con el fin de proponer nuevas estrategias que suplan o re-fuercen los enfoques tradicionales. Para tal fin, en este artículo se hace una revisión actualizada sobre las diferentes metodologías empleadas en la obtención de modelos dinámicos de carga, específicamente relacionadas con el modelo de carga compuesto. Además, y como complemento de la investigación, se presenta la aplicación de una metodología basada en mediciones para obtener un modelo de carga compuesto, basada en un algoritmo evolutivo; el desempeño del modelo obtenido se compara con un modelo de carga estático y adicionalmente se analiza su capacidad de generalización ante diferentes condiciones de operación.

CONCEPTOS BÁSICOS SOBRE MODELOS DE CARGA

Definición de carga

De acuerdo con (Rifaat, 2004), un elemento de carga se define como un dispositivo o componente de un sistema de potencia que consume, genera o controla la potencia real o reactiva; es sensible ante variaciones transitorias, dinámicas o de estado estable en la tensión de la barra donde se encuentra conectada con otros elementos, y este a su vez a una fuente de energía eléctrica. Es importante tener en cuenta que la carga no solo la conforman los dispositivos (como lámparas, motores, sistemas de aire acondicionado, por mencionar algunos), sino también hacen parte los transformadores a nivel de sub-transmisión, alimentadores primarios y secundarios, capacitores en paralelo y reguladores de tensión, entre otros.

Clasificación de modelos de carga

Para representar el comportamiento de la carga se emplean modelos, que mediante expresiones matemáticas describen las características de la potencia activa y reactiva de la carga respecto a la variación de la tensión y la frecuencia en la barra donde se encuentra conectada (Choi B. , y otros, 2006). Por simplificación, en varios estudios la frecuencia se considera constante y por tanto, los modelos solo dependen de la tensión (Kundur, 1993). De acuerdo con la forma de las expresiones matemáticas, los modelos de las cargas se clasifican en modelos estáticos y modelos dinámicos. El comportamiento en el dominio del tiempo de las cargas estáticas se representa adecuadamente por una función algebraica de la tensión y/o la frecuencia. De esta forma, se describen los modelos exponencial y polinomial o ZIP (Z, impedancia constante, I, corriente constante I y P, potencia constante) (Kundur, 1993). Las cargas dinámicas requieren un modelado explícito con ecuaciones que reflejen la dependencia de las variables con el tiempo, como en el caso de motores de inducción y síncronos. Generalmente para su representación se utilizan ecuaciones de diferencia y/o diferenciales, como el modelo utilizado en la ecuación (1).

donde P_s y Q_s representan las potencias real y re-activa de la carga en estado estable como función de la tensión V. A su vez, P_t y Q_t representan las potencias en estado transitorio como función de la tensión. T_p y T_q son las constantes de tiempo para las potencias activa y reactiva, x e y son las variables de estado para las potencias activa y reactiva, respectivamente.

Entre los modelos de carga dinámicos se encuentran el de recuperación exponencial y el modelo compuesto (Kundur, 1993). De acuerdo con la naturaleza y características de las cargas, el primero se emplea generalmente para cargas que no responden inmediatamente ante variaciones en la tensión como equipos de calefacción e iluminación, y el segundo se aplica para cargas con un considerable número de motores de inducción (Maitra, Gaikwad, Pourbeik, & Brooks, 2008) (Choi B. , y otros, 2006). En los sistemas eléctricos de potencia, la mayoría de componentes dinámicos son motores de inducción, los cuales representan un alto porcentaje de la potencia total consumida por las cargas. Por tanto, una representación mediante modelos compuestos puede aproximarse a la composición real de la carga, dado que el modelo compuesto hace parte de aquellos modelos que tienen un claro significado físico (al incluir en su composición un motor de inducción conectado en paralelo con una carga estática), comparativamente con modelos de carga de tipo “caja negra”, que no lo hacen (Song, Cotilla-Sanchez, & Brekken, 2013). Por otra parte, las aplicaciones desarrolladas con el modelo compuesto, han demostrado una buena descripción del comportamiento dinámico de la carga, específicamente para la respuesta de la potencia reactiva en estudios relacionados con estabilidad, comparativamente con modelos dinámicos de carga típicos (Peng, Yan-hong, Guoqiang, & Rui, 2005). Las razones anteriores hacen del modelo de carga compuesto uno de los más empleados y por tanto, esta revisión bibliográfica se centra en su estudio.

Este modelo, a diferencia de los otros modelos dinámicos de carga, ha sido uno de los más utilizados, debido a que tiene un claro significado físico. En su estructura combina un modelo ZIP, para representar el comportamiento estático de la carga, con un modelo de tercer orden de motor de inducción que representa el componente dinámico de la carga, que generalmente se conectan en paralelo, como se ilustra en la figura 1.

Modelo de carga compuesto (Shi & He, 2003)

Un modelo de carga compuesto combina en paralelo un modelo estático ZIP con un modelo de tercer orden de motor de inducción, como se ilustra en la figura 1, y se define como modelo de carga ZIP-IM. Es importante aclarar que a nivel de distribución, en la revision blibliográfica se encuentra la definición de un modelo compuesto como una combinación solamente de potencia constante, corriente constante e impedancia constante (Kalesar & Seifi, 2010) (Abul'Wafa, 2012). El modelo considerado en este artículo se centra en la definición inicial.

La potencia total consumida en la barra de carga de la figura 1 se puede calcular como una combinación de una parte estática y una dinámica del modelo, según la ecuación (2).

Con P₀ y Q₀ corresponden a la carga activa y re-activa inicial de la barra respectivamente, y P_motor0 y Q_motor0 son las potencias activa y reactiva inicial consumida por el motor.

La componente estática puede ser modelada a partir de la ecuación (3).

Donde P_baseZIP, Q_baseZIP representan la potencia activa y reactiva de la carga estática en estado estacionario, V₀ es la tensión de la carga en estado estacionario, a₀ y b₀ son las componentes asociadas a carga de potencia constante, a₁ y b₁ son las componentes asociadas a carga de corriente constante y a₂ y b₂ son las componentes asociadas a carga de impedancia constante. Adicionalmente, se debe cumplir la ecuación (4).

Para la componente dinámica del modelo se emplea un modelo de tercer orden de un motor de inducción, cuyas ecuaciones se presentan en la ecuación (5).

Donde las corrientes de eje d y eje q y algunos parámetros se presentan en la ecuación (6).

Donde E'_d es la fuerza electromotriz interna en el eje directo d, E'_d es la fuerza electromotriz interna en el eje en cuadratura q, ω es la velocidad del rotor, I_d e I_q son las corrientes del estator en el eje d y q respectivamente, U_d y U_q son las tensiones en terminales del eje d y del eje q. R_s , X_s , X_m , R_r y X_r son la resistencia del estator, la reactancia del estator, reactancia de magnetización, resistencia del rotor y reactancia del rotor respectivamente, y finalmente, H corresponde al coeficiente de inercia.

La potencia activa y reactiva consumida por el motor puede calcularse según la ecuación (7).

De acuerdo con las ecuaciones (2) a (7), el modelo de carga compuesto requiere 11 parámetros para su definición [R_r, X_s, X_r, R_r, X₀, H₀, T₂, a, a, b₀, b₂], los cuales se pueden obtener mediante algo-ritmos de estimación que emplean mediciones de tensiones o potencias del sistema o se definen a priori empleando parámetros típicos (Pereira, y otros, 2002) (IEEE Task Force on Load Representation for Dynamic Performances, 1995b). A continuación se presenta una revisión bibliográfica en donde se resaltan las metodologías más representativas basadas en mediciones, empleadas para la obtención del modelo de carga descrito.

REVISIÓN BIBLIOGRÁFICA DEL MODELO DE CARGA COMPUESTO

Evolución del modelo de carga compuesto

Ante la pobre representatividad y la mala precisión de los modelos de carga estáticos empleados para reproducir el comportamiento dinámico en los sistemas reales, surgieron diferentes modelos, entre ellos el modelo compuesto. Esta situación se evidenció en los estudios de validación realizados sobre los eventos del 10 de agosto de 1996 y el 4 de agosto de 2000 ocurridos en Estados Unidos. Ambos eventos estuvieron relacionados con la aparición de oscilaciones no amortiguadas, después de la salida de algunos elementos del sistema (líneas, generadores) y una serie de eventos en cascada, que condujeron posteriormente a un colapso y al aislamiento de grandes partes del sistema. Dichos eventos demostraron la necesidad de replantear los modelos de generadores y de modelos de carga estáticos existentes en el WSCC (Western Systems Coordinating Council), por modelos dinámicos, ya que con la representación original no es posible obtener una correlación entre los registros de datos y las simulaciones (Kosterev, Taylor, & Mittelstadt, 1999) (Pereira, Kosterev, Mackin, Davies, Undrill, & Zhu, 2002). En (Pereira, y otros, 2002) se propuso un modelo de carga compuesto (80% parte estática y 20% motor de inducción), el cual fue adoptado y utilizado para todas las cargas en el sistema WSCC. Los autores concluyen que la utilización de este modelo no se puede generalizar y que es susceptible de ser mejorado. La actualización del modelo anterior se hizo unos años más tarde en (Kosterev & Meklin, 2006) y (Kosterev, y otros, 2008), por parte del WECC (Western Electricity Coordinating Council, sucesor del WSCC). Allí se presenta un mejoramiento sustancial respecto al modelo anterior, en cuanto a la representación detallada de los componentes de carga en una barra dada. Entre sus ventajas más representativas se encuentra la inclusión en el modelo, de una impedancia para representar la distancia eléctrica entre la barra de transmisión y el usuario final. Adicionalmente, se considera la representación de la diversidad en la composición y en las características dinámicas de varios equipos, mediante la inclusión de cuatro tipos de motores. En la figura 2 se ilustra la estructura del modelo mejorado.

Existen numerosas referencias en donde se ha empleado el modelo de carga compuesto, así como también muchas metodologías empleadas para su ajuste. Por ejemplo, se ha empleado el enfoque basado en componentes o en mediciones para obtener los parámetros del modelo compuesto (Kundur, 1993). Para obtener un modelo de carga empleando el enfoque basado en componentes se requiere conocer en forma detallada la composición y la mezcla de la carga, lo cual generalmente es difícil de obtener. Por otra parte, el enfoque basado en mediciones es mucho más versátil, debido a que emplea las medidas obtenidas en el sistema para estimar los parámetros de una estructura definida previamente. A continuación se presentan algunas de las referencias más sobresalientes, que han empleado el enfoque basado en mediciones en la obtención de los modelos de carga compuestos, en los últimos años.

Obtención del modelo de carga compuesto empleando mediciones

En este enfoque se utilizan las mediciones adquiridas de la barra de carga para obtener el modelo. Inicialmente se selecciona una estructura para representar el comportamiento de la carga, cuyos parámetros son desconocidos. Posteriormente se emplea una metodología de estimación para determinar los parámetros mediante la minimización de la diferencia entre la respuesta del modelo estimado y las mediciones de la barra de carga (IEEE Task Force on Load Representation for Dynamic Performances, 1993) (Kundur, 1993). Las metodologías que se han empleado para estimar los parámetros del modelo compuesto de carga han sido numerosas, tanto lineales como no lineales, entre ellas se encuentran: algoritmos de mínimos cuadrados, técnicas de optimización lineal y no lineal, algo-ritmos evolutivos (Ju, y otros, 2007), entre otros. A continuación se presentan algunas de ellas.

Empleando el enfoque basado en mediciones y una metodología mixta de técnicas de identificación no lineal con modelos de predicción del error, en (Wang, Jiang, Chang, & Liu, 1994) se desarrolló un modelo de carga compuesto dependiente de la frecuencia, cuyos componentes son un circuito RC en paralelo con un circuito equivalente de un motor de inducción. Sin embargo, en este artículo no se hizo una comparación del desempeño entre el modelo compuesto dependiente de la frecuencia y el modelo convencional compuesto ante grandes excursiones de frecuencia, tensión y corriente, impidiendo verificar la validez del modelo.

En (Kao, 2001) se analiza el impacto de diversos modelos de carga (modelo dinámico de carga, compuesto y exponencial), sobre el amortiguamiento de las oscilaciones inestables de baja frecuencia ocurridas en el sistema de potencia de Taiwán, mediante el análisis de los valores propios. Allí se demuestra que el modelo compuesto, en comparación con los otros modelos, permite un mayor amortiguamiento de las oscilaciones.

Ante la influencia de los motores de inducción en el comportamiento dinámico y transitorio de los sistemas eléctricos, se han empleado técnicas para modelar un conjunto de estos elementos, mediante la obtención de un modelo equivalente por medio de la agregación de motores (Nozari, Kankam, & Price, 1987). Pero aun así, no se ha documentado por qué, mediante la representación de la carga dinámica por un motor de inducción o la combinación de este con una impedancia constante en paralelo, no se consigue una respuesta dinámica adecuada de la potencia reactiva (Xin-ran, Ren-mu, & Zhou, 1999) (Wei-guo, Ren-mu, & Tie-Qiang, 2002). Por esta razón, los autores en (Shi & He, 2003) proponen un modelo de carga compuesto mejorado, en donde consideran para la parte estática un modelo ZIP, junto con un modelo de un motor de inducción, que se valida con datos obtenidos de registros de perturbaciones transitorias.

En (De Tuglie, Patrono, & Torelli, 2005) se identifican los parámetros de un modelo compuesto de carga heterogéneo en su composición (carga dependiente del voltaje como parte estática y un motor de inducción como parte dinámica), utilizando mediciones de tensión en los nodos de carga para el modelo adaptativo, desarrollado de acuerdo con la teoría de la sensibilidad. La metodología requiere que el sistema de potencia sea excitado por perturbaciones derivadas de eventos normales del sistema y por contingencias.

Uno de los primeros artículos en donde se construye un modelo de carga compuesto (ZIP y motor de inducción) mejorado, basado en mediciones de campo corresponde a (He, Ma, & Hill, 2006), ya que la mayoría de las aplicaciones del modelo empleaban parámetros por defecto, obtenidos generalmente del software LOADSYN (General Electric Company, 1987). La metodología que se propone determina los parámetros del modelo empleando la técnica de identificación multi-curva y adicionalmente se analiza la capacidad de generalización de este modelo, mediante la técnica de validación cruzada.

En (Choi B.-K. , y otros, 2006) se presenta el desarrollo de tres modelos de carga compuestos, GZIP (modelo genérico ZIP – motor de inducción de tercer orden), Exp-IM (modelo exponencial – motor de inducción) y Z-IM (carga estática como impedancia constante y motor de inducción), cuyos parámetros fueron estimados con el algoritmo de mínimos cuadrados no lineal. Los autores concluyen que existen ciertos parámetros que se ven afectados por las condiciones de carga del motor de inducción, por lo cual es necesaria su actualización ante diferentes condiciones de operación. Aunque los tres modelos reproducen satisfactoriamente los comportamientos de potencia activa y reactiva, el modelo GZIP entrega los mejores resultados.

Uno de los problemas y retos que se presentan con el enfoque basado en mediciones en la obtención del modelo de carga radica en la gran cantidad de información que se registra y concentra en las bases de datos del sistema. Por tanto, es necesario disponer de herramientas de depuración que permitan reducir el esfuerzo computacional. En (Ma, He, & Hill, 2006), los autores proponen un modelo de carga basado en vectores de soporte que permiten obtener modelos con una gran capacidad de generalización, a partir de solo un pequeño subconjunto de las bases de datos.

En (Maitra, Gaikwad, Pourbeik, & Brooks, 2008), se empleó una metodología paramétrica no lineal, para definir estructuras compuestas del tipo (ZIP + motor de inducción). Los autores concluyen que los modelos estáticos no son apropiados para capturar la respuesta real del sistema; a su vez, que los modelos de carga obtenidos en una misma sub-estación, en el mismo instante del día e igual estación no presentan mayores variaciones entre sí.

Adicionalmente, se presenta en (Ma, Zheng, Tang, & Dong, 2009) la validación del modelo compuesto (ZIP + motor de inducción de tercer orden) obtenido mediante mediciones de campo, en donde los autores concluyen que el tamaño de la perturbación incide en gran manera en la validez del modelo de carga para determinados análisis. Se emplea un algoritmo de identificación multi-curva para minimizar los efectos del ruido sobre los resultados.

A la fecha, se han publicado muchos artículos sobre modelado de carga compuesta; sin embargo, casi todos se fundamentan en ecuaciones de carga cuyos parámetros pueden ser estimados mediante ajuste de curvas, como ya se mencionó. Debido a la complejidad asociada con las actuales cargas electrónicas, en las cuales existe una relación no lineal entre la potencia con la tensión y la frecuencia, en (Keyhani, Lu, & Heydt, 2004) se propone un modelo compuesto de carga basado en redes neuronales recurrentes. Para lograr la adecuada representación del comportamiento de las cargas empleando redes neuronales, es preciso disponer de una base de datos extensa, y por esta razón los autores entrenan con datos de simulación, que se complementan posteriormente con mediciones en línea.

Una de las conclusiones relevantes acerca de la aplicación de las redes neuronales artificiales (RNA) sobre el modelado de cargas se encuentra en (Li, Wang, & Li, 2008), donde los autores señalan que no son adecuadas para describir las características dinámicas del modelo de carga compuesto, debido a las características del algoritmo y a la estructura de la red. Por esto, los autores proponen un modelo de carga compuesto basado en la red artificial Elman con una estructura interna de realimentación.

Como ya se mencionó, una de las limitaciones que presenta el enfoque basado en mediciones es el esfuerzo computacional requerido en la estimación de modelos de carga que contengan una gran cantidad de parámetros, considerando además el tamaño actual de los sistemas de potencia y el número de cargas. El número de parámetros por determinar tiene un impacto significativo en la precisión de la metodología de estimación. Para resolver este problema, se han aplicado técnicas basadas en sensibilidad para determinar cuáles parámetros del modelo permanecen invariantes ante diversas perturbaciones, lo que permite reducir el número total de parámetros por identificar, mejorando la velocidad y precisión en la estimación como en (Xu, Si, & Qian, 2011) y (Ju, Qin, Wu, Xie, & Ning, 2011). En (Chen, Ju, Shao, & Wu, 2007) se propone la identificación de los parámetros de un modelo compuesto que comprende la red de distribución y la potencia de carga. Los autores concluyen que la constante de inercia tiene poco efecto sobre la estimación de los otros parámetros clave, en comparación con la reactancia de la red de distribución. En (Ju, y otros, 2007), los autores basados en análisis de sensibilidad del modelo de carga compuesto concluyen que los parámetros tales como porcentaje del motor en la carga total, reactancia de dispersión del estator y el deslizamiento inicial del rotor juegan un papel importante tanto en la dinámica del modelo como en la del sistema de potencia y, por tanto, es necesario estimarlos. En cambio, otros parámetros asociados al circuito del rotor o a la característica mecánica de la carga pueden considerarse constantes, debido a su poca influencia sobre la dinámica del motor, como se concluye en (Chen, y otros, 2010). Como una alternativa al esfuerzo computacional que representa la estimación de parámetros de un modelo de carga no lineal, en (Li, Xie, Yan, & Han, 2007) se propone la utilización del modelo Volterra y de patrones de clasificación, para realizar una rápida identificación en línea de los parámetros dominantes de un modelo de carga compuesto. En el año 2008, mediante mediciones de campo (Ma, Han, He, Dong, & Hill, 2008), demuestra cómo reducir el número de parámetros a estimar para mejorar la eficiencia del modelo de carga, empleando el método de la perturbación para determinar las trayectorias de sensibilidad de los parámetros del motor equivalente. Un enfoque alternativo para la reducción de esfuerzo computacional se propone en (Guoping, Jun, & Xiangsheng, 2011), a partir de métodos de agrupamiento como el algoritmo C means difuso, para la clasificación de barras e identificación de modelos de carga. Como referencia reciente, en (Son, y otros, 2014), los autores determinan cuáles parámetros del modelo de carga compuesto pueden ser ajustados en valores fijos, mediante un análisis de sensibilidad basado en las matrices Hessianas necesarias para aplicar el método de Levenberg—Marquardt.

En el área de las microredes, en (Diaz, González, Gómez, & Diez, 2010), se analiza la influencia del modelo de carga compuesto en el comportamiento oscilatorio de las mismas; adicionalmente, se comparan los resultados con los obtenidos al considerar solo modelos de carga estáticos. Una de las conclusiones obtenidas en este artículo resalta la reducción que se presenta en el margen de cargabilidad de la microred al incluir motores de inducción en el modelo de carga.

Con la creciente penetración de energías renovables, la estructura de las redes de distribución se hace más dinámica y esto puede representar una mayor complejidad en el análisis de sistemas de gran dimensión. Como una alternativa a esto, en (Zali & Milanovic, 2013) se propone un modelo equivalente dinámico de estas redes, que presente características similares al sistema original y permita reducir el tamaño de las redes actuales para el caso de estudios específicos. La estructura del modelo equivalente dinámico seleccionada es un conjunto generador-convertidor (para representar microturbinas o turbinas eólicas) en paralelo con un modelo de carga compuesto.

Por otra parte, la aplicación de algoritmos evolutivos no ha sido ajena a la obtención de los modelos de carga compuestos, debido a que han demostrado ser una herramienta útil para dar solución a problemas de optimización en otras áreas (McDonnell, Reynolds, & Fogel, 1995) (Yu & Gen, 2010) (Lee, Gonzales, Periaux, & Srinivas, 2011). Específicamente, para el modelado de carga compuesto se encuentran las siguientes referencias:

En (Ma, He, & Hill, 2006) se empleó una metodología híbrida entre algoritmos genéticos (AG) y el método de búsqueda Simplex, para determinar un conjunto óptimo de parámetros del modelo compuesto. Inicialmente, con el AG se obtienen unos valores óptimos de los parámetros iniciales y posteriormente se emplea el método de búsqueda Simplex para construir el modelo. En (Ma, He, & Hill, 2007) se utilizan los AG para estimar trece parámetros de un modelo de carga compuesto basado en mediciones, el cual fue comparado después con un modelo obtenido con el método de mínimos cuadrados no lineales. Con mediciones en el sistema de transmisión, se presenta en (Zhang & Bai, 2008) la obtención de modelos de carga compuestos. Como el problema de estimación de parámetros para este caso es no lineal, se emplea un método con algoritmos genéticos, en el cual se mejora la dirección de búsqueda óptima, la forma de mantener a los mejores individuos y una estrategia de emigración que permite evitar la convergencia a soluciones locales. Se comparan los resultados obtenidos respecto a los entregados con el método de Levenberg-Marquardt (LM). Los autores concluyen que se debe ser prudente con la propuesta realizada, ya que aunque los resultados numéricos entregados por el algoritmo genético son una buena aproximación, este requiere más tiempo computacional que el algoritmo LM. Para redes eléctricas a gran escala, se muestra en (Han, Ma, He, & Dong, 2009) el desarrollo de un modelo de carga basado en mediciones de campo. Inicialmente se hace una clasificación de los nodos para determinar la ubicación adecuada de los dispositivos de medición. Después se estiman los parámetros de un modelo ZIP en paralelo con un motor de inducción, empleando un híbrido entre AG y método de búsqueda Simplex. El algoritmo genético se aplica inicialmente para determinar las regiones en las que se puede encontrar el óptimo (definido como el conjunto de parámetros) y posteriormente se emplea el método de búsqueda Simplex para determinar su valor. En (Choi, Chiang, & Yu, 2009) se muestra la estimación de los parámetros de un modelo de carga compuesto, mediante optimización basada en Trust-Tech. La estimación de parámetros se plantea como un problema de optimización no lineal con restricciones. Los autores concluyen que la metodología se puede aplicar exitosamente en la estimación de parámetros del modelo compuesto planteado, ya que la técnica permite obtener múltiples mínimos locales, de los cuales se puede determinar el valor óptimo. Los autores en (Choi & Chiang, 2009) proponen como alternativas al problema de múltiples soluciones que se pueden presentar, reducir el número de parámetros del modelo de carga (ZIP o exponenciales), mediante la formulación de un problema de programación cuadrática con restricciones lineales, más que como mínimos cuadrados no lineales. En (Wang, Han, & Ma, 2010) se hace un análisis de sensibilidad sobre los parámetros; aquellos más sensibles son identificados utilizando AG y los menos sensibles son ajustados a valores fijos.

Además de la aplicación de AG, se encuentran técnicas nuevas como el Harmony Search Algorithm que están siendo adaptadas para su aplicación al modelado de carga compuesta en redes de distribución (Alinejad, Akbari, & Kazemi, 2012). Por otra parte, debido a la disponibilidad de mediciones sincronizadas, se proponen nuevos enfoques en (Najafabadi & Alouani, 2012), para el desarrollo de modelos a partir de la estimación en línea, para suplir los problemas de la estimación convencional fuera de línea (requerimientos de esfuerzo computacional y memoria).

Como una aplicación de PSO (Particle Swarm Optimization) en la obtención de modelos de carga compuestos, se encuentra (Rodriguez, Perez, & Mora, 2013), en donde se propuso una modificación al algoritmo original, consiguiendo mejorar las soluciones obtenidas por este. El algoritmo genera una población inicial, la cual se desplaza a través del espacio de soluciones a partir de la información de las mejores soluciones encontradas por cada partícula y por el enjambre en su conjunto. Una dificultad del algoritmo PSO original es que las velocidades de desplazamiento de las partículas en el espacio de soluciones decrecen a medida que avanza el proceso iterativo; en este escenario, el algoritmo se enfoca en una búsqueda local; sin embargo, se limita para encontrar soluciones en regiones no exploradas. Por tanto, se implementa un mecanismo denominado reinicio de velocidad, que permite generar un conjunto nuevo de velocidades cuando estas son menores a una tolerancia, lo que finalmente ayuda al algoritmo a determinar posibles soluciones óptimas en otras regiones del espacio de soluciones.

Como referencias actuales se encuentra (Aree, 2014), en donde se presenta una metodología para incorporar las características no lineales de las cargas reales en el análisis de flujo de carga, mediante modelos compuestos. En contraste con el cálculo convencional de flujos de carga, en esta propuesta se obtienen mejores resultados debido al reajuste en forma separada de las potencias activa y reactiva de cada motor y carga estática, ante variaciones de tensión durante el proceso iterativo.

Por último, se aprecia en la revisión de la literatura un reciente interés por considerar el efecto de los motores de inducción en la estabilidad a corto plazo, debido a su rápida tendencia de restauración de potencia consumida ante un evento. Es así como en (Xu, y otros, 2014) se propone una metodología para determinar la ubicación óptima de compensación dinámica de reactivos, considerando cargas compuestas.

APLICACIÓN DE MODELADO DE CARGA COMPUESTA BASADO EN MEDICIONES

Desarrollo de un modelo de carga compuesto a partir de mediciones

Con el fin de validar la respuesta del modelo de carga compuesto, ampliamente analizada en la revisión bibliográfica de este artículo, en esta sección se presentan los resultados del modelo estimado, al utilizar los datos obtenidos de las simulaciones realizadas sobre el sistema IEEE de 30 barras (University of Washington, 1999). Con el fin de simular un efecto dinámico en la respuesta de la carga, el sistema IEEE de 30 barras se modifica mediante la inclusión de motores de inducción (con torque mecánico constante), en la barra 29 del sistema. Los parámetros del modelo de carga se estiman empleando el algoritmo mejorado de optimización por enjambre de partículas (PSO) presentado en (Rodriguez, Perez, & Mora, 2013) y explicado en la sección anterior. Para estimar los parámetros del modelo se utiliza la información de la magnitud y el ángulo de tensión, potencia activa y reactiva en la barra de carga, obtenidos en el caso de una falla trifásica de 200 ms en la línea que conecta las barras 25 y 27. Se considera la presencia de ruido en las mediciones, con el fin de representar condiciones cercanas a las reales en los equipos de medición. La señal de ruido que se agrega es una señal aleatoria, generada mediante una distribución normal, la cual tiene media cero y desviación estándar de 0,005.

Los resultados de la estimación y su comparación con las mediciones de la respuesta de la carga se muestran en la figura 3. Para cuantificar el error en la estimación se emplea la ecuación (8).

Donde N es el número de muestras de la ventana de tiempo a analizar, 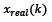corresponde a la medición en el instante corresponde a la estimación del modelo de carga en el instante k. Este indicador se calcula de manera independiente para la potencia activa y reactiva.

Los resultados de la estimación muestran que la respuesta del modelo de carga compuesto se ajusta de manera satisfactoria a los datos adquiridos del sistema de potencia, y la presencia de ruido en estos no presenta efectos considerables en la respuesta del modelo de carga. En la tabla 1 se presenta el conjunto de parámetros que se obtienen al final del proceso de optimización.

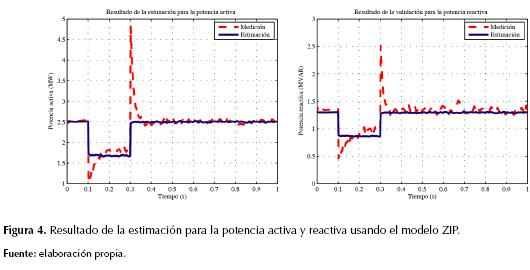
Para mostrar la importancia de la utilización de modelos dinámicos de carga, se propone a modo de comparación la estimación de un modelo de carga estático del tipo ZIP para emular la respuesta de la carga en la barra 29. Los resultados de la estimación se muestran en la figura 4 y el conjunto de parámetros obtenidos, en la tabla 2.

A diferencia del modelo de carga compuesta, el desempeño del modelo ZIP es deficiente para reproducir el comportamiento dinámico de la carga, específicamente en su parte transitoria, ya que la respuesta del modelo depende únicamente de la tensión instantánea del modelo de carga y no tiene en cuenta otros tipos de variables dinámicas que caracterizan las cargas. La tabla 3 presenta un comparativo del desempeño del modelo compuesto y el modelo ZIP empleando en la ecuación (8).

El indicador de error demuestra el resultado visualizado en la figura 4, en donde los errores en el modelo ZIP se duplican en comparación con el modelo compuesto, tanto para potencia activa como potencia reactiva. Esto confirma como ya se ha reportado en algunas referencias (Kundur, 1993), (Choi B.-K. , y otros, 2006), que la utilización del modelo ZIP no es apropiado para representar respuestas dinámicas significativas de la carga ante perturbaciones en el sistema.

Validación de la capacidad de generalización del modelo compuesto

Una de las principales preguntas que se hacen al obtener un modelo de carga está relacionada con su capacidad de generalización, es decir, si el modelo es válido para otras condiciones de operación diferentes a las cuales fue ajustado. Para analizar esta característica del modelo de carga compuesto obtenido, se hace una prueba de validación cruzada para comprobar la precisión del modelo. Se obtienen mediante simulación datos de la respuesta de la carga de la barra 29 en magnitud de tensión, ángulo de tensión, potencia activa y potencia reactiva, ante 4 diferentes perturbaciones (falla trifásica, salida de transformador, pérdida de excitación de un generador y salida de línea). La prueba de validación cruzada se desarrolló de la siguiente manera.

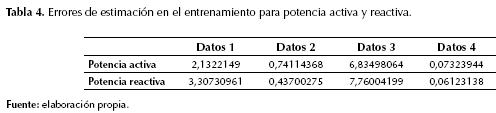
Inicialmente se obtiene el modelo de carga utilizando el conjunto de datos de la primera perturbación. Una vez desarrollado el modelo, se valida su respuesta con los datos de las demás perturbaciones, obteniendo para cada caso un error de validación. El procedimiento se repite desarrollando el modelo con el siguiente conjunto de datos y luego validando su respuesta con los conjuntos de datos restantes. La tabla 4 resume los errores obtenidos durante el desarrollo de los modelos de carga con cada uno de los conjuntos de datos de perturbaciones.

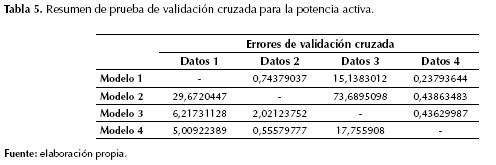
En la tabla 4, los datos 1 y 3 corresponden a perturbaciones severas (falla trifásica y pérdida de excitación), mientras que los datos 2 y 4 corresponden a perturbaciones leves (salida de transformador y salida de línea). El ajuste del modelo es mejor cuando los efectos transitorios son suaves, como es el caso de las perturbaciones pequeñas; sin embargo, errores bajos no garantizan que el modelo responda satisfactoriamente ante diversas condiciones de operación, esto es, no garantiza su capacidad de generalización. En las tablas 5 y 6 se presentan los errores de validación cruzada para cada conjunto de datos de entrenamiento. Las filas representan los datos empleados para la obtención del modelo, y las columnas representan el error de validación del modelo con los otros conjuntos de datos.

De las tablas 5 y 6, se observa que los errores en los modelos obtenidos con datos de perturbación severa (modelos 1 y 3), cuando se validan con datos de perturbación leve (datos 2 y 4) son menores en comparación con la situación contraria, en donde los modelos desarrollados con datos de perturbación leve (modelos 2 y 4) se validan con datos de perturbación severa (datos 1 y 2). Esta afirmación se puede corroborar cualitativamente con los siguientes casos puntuales de las pruebas de validación. Inicialmente, se ilustra el caso de la validación con los datos de perturbación leve (conjunto de datos 4), cuando el modelo se obtiene con los datos de perturbación severa (conjunto de datos 1). La figura 5 muestra la respuesta en potencias activa y reactiva cuando se efectúa la salida de la línea 27-30; además se presenta la respuesta del modelo de carga. También se observa en este caso que la respuesta se ajusta de manera adecuada a los datos y la respuesta se aproxima al comportamiento transitorio de la carga.

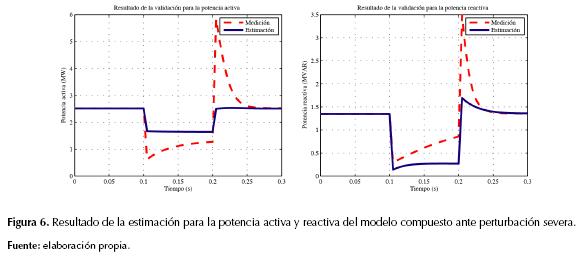
Sin embargo, es importante analizar la situación contraria. Ahora se muestra el caso de la prueba de validación con una perturbación severa (conjunto de datos 3), cuando el modelo se obtiene con datos de una perturbación leve (conjunto de datos 4). La figura 6 presenta la respuesta del modelo de carga y del sistema, cuando se pierde la excitación del generador síncrono. En este caso, la perturbación es severa considerando la magnitud de la desviación en las potencias.

De acuerdo con las figuras anteriores, así como con los resultados de las tablas 5 y 6, es evidente que existen errores considerables entre los datos adquiridas del sistema con la respuesta del modelo de la carga. Debido a que el entrenamiento se hace con datos de una perturbación leve, el modelo de carga no captura el comportamiento dinámico que presenta la carga cuando las variaciones de tensión son severas. Por tanto, la validación presenta errores superiores en comparación con el caso anterior. A partir de la prueba de validación, se destaca la importancia de la utilización de datos adecuados de la respuesta real de la carga en el sistema de potencia, con el fin de que el modelo represente mejor su comportamiento. Las mediciones por emplear dependen también de la estructura del modelo de carga, aunque en el caso del modelo compuesto es deseable utilizar mediciones de perturbaciones en donde las variaciones de tensión sean superiores a 20% de la tensión nominal, de acuerdo con los resultados presentados en la tabla 4.

Conclusiones

En este documento se presenta una recopilación de algunas de las metodologías utilizadas para la obtención de modelos de carga compuestos, con el fin de facilitar el análisis de las tendencias en cuanto a enfoques y nuevas propuestas en la temática de estudio. Esta área de investigación, aunque ha sido tratada hace más de tres décadas, continúa vigente debido a que involucra características dinámicas y complejas del sistema de potencia y de su creciente necesidad de mejor representación de fenómenos físicos.

Como aporte adicional, se presentó un modelo compuesto basado en mediciones (datos obtenidos bajo simulación), que permite reproducir satisfactoriamente la respuesta de una carga dinámica ante una perturbación, comparativamente con un modelo estático. Posteriormente, se comprueba que la capacidad de generalización del modelo compuesto obtenido depende del tipo y magnitud de la perturbación que fue empleado para la estimación. Cuanto mayor sea la variación de tensión empleada en la estimación, el modelo presentará más posibilidades de representar las características de la carga bajo otras variaciones. Esta conclusión obliga a considerar una limitación que presentan los modelos de carga compuestos, que emplean las mediciones obtenidas en condiciones operativas normales y, por tanto, es preciso disponer de herramientas de monitorización permanente en el sistema para lograr capturar respuestas transitorias de mayor magnitud. Esto puede conseguirse mediante la utilización masiva de la información suministrada por los sistemas de monitorización de área amplia en los sistemas de potencia.

Referencias

Abdelaziz, A.; Badr, M., & Younes, A. (Nov. 2007). Dynamic load modeling of an Egyptian primary distribution system using neural networks. International Journal of Electrical Power & Energy Systems, 29(9), 637-649.         [ Links ]

Abul'Wafa, A. (2012). A network-topology-based load flow for radial distribution networks with compo site and exponential load. Electric Power Systems Research, 91, 37-43.         [ Links ]

Alinejad, B.; Akbari, M., & Kazemi, H. (2012). PMU-based distribution network load modelling using Harmony Search Algorithm. Proceedings of 17th Conference on Electrical Power Distribution Networks, pp. 1-6.         [ Links ]

Aree, P. (2014). Power Flow Computation Considering Nonlinear Characteristics of Composite Load Model. Proceedings of the International Electrical Engineering Congress (iEECON), pp. 1-4.         [ Links ]

Chen, D., & Mohler, R. (July 2003). Neural-Network-Based Load Modeling and its Use in Voltage Stability Analysis. IEEE Transactions on Control Systems Technology, 11(11), 460-470.         [ Links ]

Chen, Q.; Ju, P.; Shao, Z.-Y., & Wu, F. (2007). Electrical Load Modeling with Considering Distribution Network. Proceedings of 2007 iREP Symposium Bulk Power System Dynamics and Control, pp. 1-6.         [ Links ]

Chen, Q.; Ju, P.; Shi, K.; Tang, Y.; Shao, Z., & Yang, W. (2010). Parameter estimation and comparison of the load models with considering distribution network directly and indirectly. International Journal of Electrical Power and Energy Systems, 32(9), 965-968.         [ Links ]

Choi, B., & Chiang, H. (May 2009). Multiple Solutions and Plateau Phenomenon in Measurement-Based Load Model Development: Issues and Suggestions. IEEE Transactions on Power Systems, 24(2), 824-831.         [ Links ]

Choi, B.; Chiang, H., & Yu, D. (2009). Trust-Tech based Parameter Estimation and its Application to Power System Load Modeling. Proceedings of IEEE PES General Meeting. Calgary.         [ Links ]

Choi, B.; Chiang, H.; Li, Y.; Li, H.; Chen, Y.; Huang, D., & Lauby, M. (Aug. 2006). Measurement-based Dynamic Load Models: Derivation, Comparison and Validation. IEEE Transactions on Power Systems, 21(3), 1276-1283.         [ Links ]

Choi, B.-K.; Chiang, H.-D.; Li, Y.; Chen, Y.-T.; Huang, D.-H., & Lauby, M. (2006). Development of Composite Load Models of Power Systems using On-line Measurement Data. Proceedings of IEEE PES General Meeting. Montreal.         [ Links ]

De Tuglie, E.; Patrono, G., & Torelli, F. (2005). A sensitivity-based approach for static and dynamic load parameter estimation. Proceedings of IEEE Russia Power Tech. St. Petersburg.         [ Links ]

Department of Energy and Climate Change (DECC). (2010). Energy Trends: Electricity and Electricity Consumption in the UK. National Statistics Publications.         [ Links ]

Diaz, G.; González, C.; Gómez, J., & Diez, A. (2010). Composite Loads in Stand-Aline Inverter-Based Mi-crogrids-Modeling Procedure and Effects on Load Margin. IEEE Transactions on Power Systems, 25(2), 894-905.         [ Links ]

General Electric Company (1987). EPRI Final Report EL5003: Load modeling for powerflow and transient stability computer studies.         [ Links ]

Guoping, S.; Jun, L., & Xiangsheng, L. (2011). Load clustering and synthetic modeling based on an improved fuzzy C means clustering algorithm. Proceedings of 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, pp. 859-865. Shandong.         [ Links ]

Han, D.; Ma, J.; He, R.-M., & Dong, Z.-Y. (2009). A Real Application of Measurement-Based Load Modeling in Large Scale Power Grids and Its Validation. IEEE Transitions on Power Systems, 24(4), 1756-1764.         [ Links ]

He, R.-M.; Ma, J., & Hill, D. (May 2006). Composite Load Modeling via Measurement Approach. IEEE Transactions on Power Systems, 21(2), 663-672.         [ Links ]

IEEE Task Force on Load Representation for Dynamic Performances. (May 1993). Load representation for dynamic perfomance analysis. IEEE Transactions on Power Systems, 8(2), 472-482.         [ Links ]

IEEE Task Force on Load Representation for Dynamic Performances. (Feb. 1995a). Bibliography on load models for power flow and dynamic perfomance simulation. IEEE Transactions on Power Systems, 10(1), 523-538.         [ Links ]

IEEE Task Force on Load Representation for Dynamic Performances. (Aug. 1995b). Standard Load Models for Power Flow and Dynamic Performance Simulation. IEEE Transactions on Power Systems, 1302-1313.         [ Links ]

Ju, P.; Qin, C.; Wu, F.; Xie, H., & Ning, Y. (2011). Load modeling for wide area power system. Electrical Power and Energy Systems, 33, 909-917.         [ Links ]

Ju, P.; Wu, F.; Shao, Z.-Y.; Zhang, X.-P.; Fu, H.-J.; Zhang, P.-F.; . . . Han, J.-D. (Sept. 2007). Composite load models based on field measurements and their applications in dynamic analysis. IET Generation, Transmission and Distribution, 1(5), 724-730.         [ Links ]

Kalesar, B., & Seifi, A. (2010). Fuzzy load flow in balanced and unbalanced radial distribution systems incorporating composite load model. Electrical Power and Energy Systems, 17-23.         [ Links ]

Kao, W. (Aug. 2001). The Effect of Load Models on Unstable Low-Frequency Oscillation Damping in Taipower System Experience w/wo Power System Stabilizers. IEEE Transactions on Power Systems, 16(3), 463-472.         [ Links ]

Keyhani, A.; Lu, W., & Heydt, G. (2004). Composite Neural Netwrok Load Models for Power System Stability Analysis. Proceedings of IEEE Power Systems Conference & Exposition, pp. 1159-1163.         [ Links ]

Knyazkin, V.; Cañizares, C., & Söder, L. (May 2004). On the Parameter Estimation and Modeling of Aggregate Power System Loads. IEEE Transactions on Power Systems, 19(2), 1023-1031.         [ Links ]

Kosterev, D., & Meklin, A. (2006). Load Modeling in WECC. Proceedings of Power Systems Conference and Exposition PSCE, pp. 576-581.         [ Links ]

Kosterev, D.; Meklin, A.; Undrill, J.; Lesieutre, B.; Price, W.; Chassin, D., . . . Yang, S. (2008). Load Modeling in Power System Studies: WECC Progress Update. Proceedings of PES General Meeting, pp. 1-8.         [ Links ]

Kosterev, D.; Taylor, C., & Mittelstadt, W. (Aug. 1999). Model validation for the August 10, 1996 WSCC system outage. IEEE Transactions on Power Systems, 14(3), 967-979.         [ Links ]

Kundur, P. (1993). Power System Stability and Control. New York: McGraw-Hill.         [ Links ]

Lee, D.; Gonzales, L.; Periaux, J., & Srinivas, K. (Apr. 2011). Efficient hybrid-game strategies coupled to evolutionary algorithms for robust multidisciplinary design optimization in aerospace engineering. IEEE Transactions on Evolutionary Computation, 15(2), 133-150.         [ Links ]

Li, L.; Xie, X.; Yan, J., & Han, Y. (2007). Fast Online Identification of the Dominant Parameters of Composite Load Model Using Volterra Model and Pattern Classification. Proceedings of IEEE PES General Meeting, pp. 1-8.         [ Links ]

Li, X.; Wang, L., & Li, P. (2008). The Study on Composite Load Model Structure of Artificial Neural Network. Proceedings of 3rd International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. NanJing. pp. 1564-1570.         [ Links ]

Ma, J.; Han, D.; He, R.-M.; Dong, Z.-Y., & Hill, D. (2008). Reducing Identified Parameters of Measurement-Based Composite Load Model. IEEE Transactions on Power Systems, 23(1), 76-83.         [ Links ]

Ma, J.; He, R., & Hill, D. (May 2006). Load Modeling by Finding Support Vectors of Load Data from Field Measurements. IEEE Transactions on Power Systems, 21(2), 726-735.         [ Links ]

Ma, J.; He, R.-M., & Hill, D. (2007). Measurement-based Load Modeling using Genetic Algorithms. Proceedings of IEEE Congress on Evolutionary Computation, pp. 2909-2916.         [ Links ]

Ma, J.; Zheng, X.-Y.; Tang, Y.-H., & Dong, Z.-Y. (2009). Validating Measurement-Based Composite Load Model. Proceedings of 8th International Conference on Advances in Power System Control, Operation and Management, pp. 1-6.         [ Links ]

Maitra, A.; Gaikwad, A.; Pourbeik, P., & Brooks, D. (2008). Load Model Parameter Derivation Using an Automated Algorithm and Measured Data. Proceedings of IEEE PES Conversion and Delivery of Electrical Energy in the 21st Century, pp. 1-7.         [ Links ]

Mauricio, W., & Semlyen, A. (Nov. 1972). Effect of load characteristics on the dynamic stability of power systems. IEEE Transactions on Power Apparatus and Systems, 14(3), 2295-2304.         [ Links ]

McDonnell, J.; Reynolds, J., & Fogel, D. (1995). Special Session on Applications of evolutionary computation to biology and biochemistry. MIT Press.         [ Links ]

Milanovic, J.; Yamashita, K.; Martinez, S.; Djokie, S., & Korunovic, L. (Aug. 2013). International Industry Practice on Power System Load Modeling. IEEE Transactions on Power Systems, 28(3).         [ Links ]

Najafabadi, A., & Alouani, A. (2012). Real time estimation of sensitive parameters of composite power system load model. Proceedings of 2012 IEEE Power and Energy Society Transmission and Distribution Conference and Exposition. Orlando. pp. 1-8.         [ Links ]

Nozari, F.; Kankam, M., & Price, W. (Nov. 1987). Aggregation of Induction Motors for Transient Stability Load Modeling. IEEE Transactions on Power Systems, 2(4), 1096-1103.         [ Links ]

Ornata, T., & Uemura, K. (Nov. 1998). Aspects of Voltage Responses of Induction Loads. IEEE Transactions on Power Systems, 13(4), 1337-1344.         [ Links ]

Peng, W.; Yan-hong, W.; Guo-qiang, H., & Rui, M. (2005). Study on the Reduction of Identified Parameters of the Power Load's Aggregated Motor Model with the AIm of Sustaining Its Representabilidad. Proceedings of IEEE PES Transmission and Distribution Conference and Exhibition: Asia and Pacific.         [ Links ]

Pereira, L.; Kosterev, D.; Mackin, P.; Davies, D.; Undrill, J., & Zhu, W. (Nov. 2002). An Interim Dynamic Induction Motor Model for Stability Studies in the WSCC. IEEE Transactions on Power Systems, 17(4), 1108-1115.         [ Links ]

Rifaat, R. (2004). On Composite Load Modeling for Voltage Stability and Under Voltage Load Shedding. Proceedings of IEEE PES General Meeting, pp. 1603-1610).         [ Links ]

Rodriguez, L.; Perez, S., & Mora, J. (2013). Particle Swarm Optimization applied in Power System Measurement-Based Load Modeling. Proceedings of IEEE Congress on Evolutionary Computation, pp. 2368-2375. Cancún.         [ Links ]

Shi, G.; Peng, G., & Liu, X. (2012). Comparative Research on Power Load Modeling Method in Power Electrical System. Proceedings of Fifth International Conference on Intelligent Computation Technology and Automation (ICICTA), pp. 455-458.         [ Links ]

Shi, J., & He, R. (2003). Measurement-based load modeling-model structure. Proceedings of IEEE Power-Tech Conference. Bologna.         [ Links ]

Son, S.; Lee, S.; Choi, D.; Song, K.; Park, J.; Kwon, Y., . . . Park, J. (2014). Improvement of Composite Load Modeling Based on Parameter Sensitivity and Dependency Analyses. IEEE Transactions on Power Systems, 242-250.         [ Links ]

Song, J.; Cotilla-Sanchez, E., & Brekken, T. (2013). Load Modeling Methodologies for Cascading Outage Simulation Considering Power System Stability. 1st IEEE Conference on Technologies for Sustainability (SusTech), pp. 78-85.         [ Links ]

University of Washington. (1999). Electrical Engineering. Obtenido de http://www.ee.washington.edu/ research/pstca/.         [ Links ]

Wang, J.; Han, M., & Ma, J. (2010). A New Identification Strategy for Improving Convergence Stability of Load Model Parameters. Proceedings of International Conference on Electrical and Control Engineering, pp. 45-148.         [ Links ]

Wang, J.; Jiang, H.; Chang, C., & Liu, A. (Feb. 1994). Development of a frequency-dependent composite load model using measurement approach. IEEE Transactions on Power Systems, 9(3), 1546-1556.         [ Links ]

Wang, J.; Li, X.; Su, S., & Xia, X. (2006). Research on Dunamic Load Modeling Using Back Propagation Neural Network for Electric Power System. Proceedings of International Conference on Power System Technology, pp. 1-4.         [ Links ]

Wei-guo, W.; Ren-mu, H., & Tie-Qiang, W. (2002). The induction motor model to reflect dynamic mechanism of synthetic load. Automation of Electric Power Systems, 26(4), 23-27.         [ Links ]

Wen, J.; Jiang, L.; Wu, Q., & Cheng, S. (2003). Power System Load Modeling by Learning Based on System Measurements. IEEE Transactions on Power Delivery, 18(2), 364-371.         [ Links ]

Wu, Q.; Wen, J.; Nuttall, K.; Shimmin, D., & Cheng, S. (2003). Power System Load Modeling by Evolutionary Computation Based on System Measurements. Electric Power Components and Systems, 31(5), 423-439.         [ Links ]

Xin-ran, L.; Ren-mu, H., & Zhou, W. (1999). The General Induction Motor Model and its description ability for synthetic loads for electric power system. Journal of North China Electric Power University, 26(1).         [ Links ]

Xu, Y.; Dong, Z.; Meng, K.; Yao, W.; Zhang, R., & Wong, K. (2014). Multi-Objective Dynamic VAR Planning Against Short-Term Voltage Instability Using a Decomposition-Based Evolutionary Algorithm. IEEE Transactions on Power Systems, 29(6), 2813-2822.         [ Links ]

Xu, Y.; Si, D., & Qian, Y. (2011). Research on Feasibility of Composite Load Modeling Based on WAMS. Proceedings of 2011 Asia-Pacific Power and Energy Engineering Conference, pp. 1-4. Wuhan.         [ Links ]

Yu, X., & Gen, M. (2010). Introduction to Evolutionary Algorithms (Decision Engineering). London: Springer-Verlag.         [ Links ]

Zali, S., & Milanovic, J. (2013). Generic Model of Active Distribution Network for Large Power System Stability Studies. IEEE Transactions on Power Systems, 28(3), 3126-3133.         [ Links ]

Zhang, P., & Bai, H. (2008). Derivation of Load Model Parameters using Improved Genetic Algorithm. Proceedings of International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, pp. 970-977.         [ Links ]