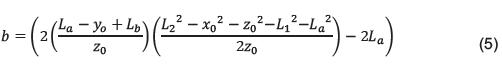¹Ph.D. Automática y Robótica. M.Sc. Ing. Electromecánico. Docente Universidad de Pamplona. Programa de Ing. Mecatrónica. Pamplona, Colombia.
cesarapc@unipamplona.edu.co
²M.Sc. (c) Ing. Mecánico. Docente Universidad de Pamplona. Programa de Ing. Mecánica. Pamplona, Colombia.
edisonmartinez@unipamplona.edu.co
³Ph.D. (c). M.Sc. Ing. Electrónico. Investigador Universidad Politécnica de Madrid, Docente Universidad Nacional de Colombia. Programa de Ing. Mecatrónica. Bogotá, Colombia.
pfcardenash@unal.edu.co

Fecha de recepción: 19 de enero de 2011 Fecha de aprobación: 30 de junio de 2011

RESUMEN

Este artículo presenta el cálculo óptimo de las dimensiones de un robot paralelo tipo delta basado en el menor consumo de energía. También incluye la descripción de la plataforma experimental, y un análisis cinemático y dinámico. El algoritmo de optimización (algoritmos genéticos), tiene en cuenta restricciones tales como: cubrimiento de un espacio de trabajo semiesférico de un radio específico y el análisis de interferencias.

Palabras clave: robots paralelos, optimización, diseño verde, algoritmos genéticos.

ABSTRACT

This paper presents an optimal dimension estimation of a Delta parallel robot based on a lower energy consumption. It also presents the description of the experimental platform, kinematic and dynamic analysis. The optimization algorithm (genetic algorithms) takes into account restrictions, such as covering a semi-spherical workspace with a specific radius and the interference analysis.

Key words: parallel robots, optimization, green design, genetic algorithms.

INTRODUCCIÓN

El interés mundial en las tecnologías verdes crece continuamente. Una de las principales razones de este incremento, es la concientización de las personas sobre el buen trato del medio ambiente. Las industrias se han dado cuenta que el desarrollo de productos sostenibles no sólo ayuda al medio ambiente, sino que les produce retribuciones económicas.

La robótica y la automatización como era de esperarse, no se han quedado atrás en el desarrollo de productos que contribuyan con este objetivo [1]. La nueva era de robots plantea fundamentos en un consumo mínimo de energía [2], [3], [4] y [5], uso de materiales reciclables, actuadores silenciosos y con elevados niveles de eficiencia, etc. [6], [7], [8], [9] y [10].

El grupo de automatización y control (A&C), de la Universidad de Pamplona, se encuentra desarrollando diversos dispositivos robóticos en los cuales se ha planteado el objetivo de usar o generar técnicas de diseño de productos sostenibles. Por ejemplo: en este trabajo, se presenta una optimización dimensional de los eslabones de un robot paralelo tipo delta [11], con el fin de consumir la menor cantidad de energía en el desarrollo de una trayectoria predefinida que cubre unos puntos significativos del espacio de trabajo para el cual se está diseñando el robot. La optimización basada en energía, garantiza un reducido consumo de corriente eléctrica, colaborando con el medio ambiente y haciendo más rentables los procesos en los cuales utiliza el robot.

Por otra parte, debe tenerse en cuenta que uno de los factores que más influye en el consumo de energía del robot, es el tamaño de los eslabones del mismo y por lo cual, el diseño de un robot basado en una optimización de energía, tenderá a generar dimensiones reducidas, lo cual implica un menor consumo de materia prima en su construcción y contribuye con el medio ambiente. Además, los materiales seleccionados para construir el robot, son en su mayoría: aluminio, acrílico y fibra de vidrio debido por ser reciclables.

El artículo se encuentra dispuesto de la siguiente forma: en la sección dos, se hace una descripción del robot paralelo y la plataforma experimental. En la sección tres, se presenta el análisis cinemático de la estructura paralela que se utiliza para obtener el espacio de trabajo. La sección cuatro, presenta el modelo dinámico usado para calcular la potencia y la energía. La sección cinco, explica las restricciones utilizadas para verificar que los prototipos de los robots tengan la capacidad de cubrir el espacio de trabajo impuesto. La sección seis, exhibe las técnicas de optimización planteadas para calcular las dimensiones del robot. La sección siete, expone los resultados obtenidos y un análisis de los mismos, y por último, en la sección ocho se presentan las conclusiones del trabajo.

1. DESCRIPCIÓN DEL ROBOT

El diseño del robot paralelo tipo delta [11] hace parte una plataforma experimental que tiene como objetivo facilitar la enseñanza de diversos temas tales como: robots paralelos, control cinemático y dinámico de robots, sistemas avanzados de control, teleoperación de robots, teniendo en cuenta el retardo en el canal de comunicaciones, etc.

En la figura 1. Se puede apreciar el diagrama esquemático de la plataforma, que se puede describir en dos partes fundamentales: Una de ellas, está conformada por el robot paralelo, un sistema de control de bajo nivel, un sistema de comunicaciones, un sistema de protección y tratamiento de emergencias.

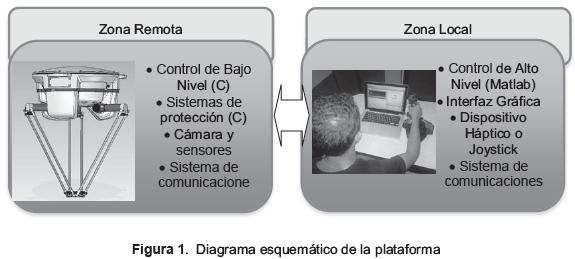
El control a bajo nivel, se encarga de controlar los accionamientos del robot, de tal forma que se pueda lograr las referencias o señales dadas por el control a alto nivel. A su vez, el control a bajo nivel se encarga de capturar y transmitir las medidas de los sensores. El control a bajo nivel tiene tres modos de operación: control por corriente, por velocidad y por posición. Estos modos de operación aportan la flexibilidad necesaria para implementar los principales esquemas de control de alto nivel.

El sistema de protección y tratamiento de emergencias, se encarga de verificar continuamente los movimientos del robot, evitando las colisiones y posibles daños de sus propios componentes. Este sistema se implemento, teniendo en cuenta que la plataforma se utilizará para la corroboración experimental de diferentes sistemas de control diseñados por estudiantes, por lo cual, pueden contener errores que desestabilizan los accionamientos del sistema. Este sistema debe ser capaz de detectar las posibles anomalías o emergencias y tratarlas en forma adecuada para evitar daños al robot. Todos los algoritmos de control de bajo nivel, el sistema de comunicaciones y el sistema de protección y tratamiento de emergencias, fueron implementados con el fin de ejecutar un gran número de operaciones con una frecuencia muy alta.

La otra parte de la plataforma experimental está compuesta por el controlador de alto nivel, el sistema de comunicaciones y opcionalmente, dispositivos de entrada con o sin reflexión de fuerzas. Con el fin de facilitar el aprendizaje de los estudiantes, se eligió Matlab (R) como el software para implementar el control a alto nivel, que permite la implementación rápida de diversos controladores y el uso de diversos tipos de librerías que facilitan crear controladores con mucha complejidad, tales como controladores robustos, adaptativos, deslizantes, no lineales, difusos, neuronales, híbridos, etc.

La comunicación entre las dos partes de la plataforma se hace, enviando mensajes y utilizando el protocolo de datagramas de usuario (Comunicación UDP). Este tipo de comunicación es muy rápida y permite ubicar las dos partes de la plataforma sobre el mismo computador o si se desea, se puede ubicar en diferentes computadores conectados por medio de una red LAN.

Uno de los objetivos de seleccionar este tipo de comunicación, es poder montar en el laboratorio de robótica de la Universidad, un módulo que contenga el robot y sus accesorios físicos, de forma que los estudiantes de diferentes universidades, por medio de un sistema de gestión de usuarios, puedan acceder a él y corroboren el sistema de control que estén diseñando.

Los estudiantes sólo requirieren poseer Matlab ( R) que es una herramienta muy común hoy en día, en el campo de la ingeniería. La idea es que los estudiantes bajen de Internet una plantilla elaborada en simulink, que contiene los bloques correspondientes al modelo cinemático y dinámico de robot, la interfaz gráfica y el bloque de comunicación con el robot real. De esta forma, por medio de unos interruptores en simulink, los usuarios podrán seleccionar dos modos de funcionamiento: modo simulación y modo experimental. Así, una vez los estudiantes hayan construido los controladores y los hayan simulado exitosamente, se podrán conectar con el laboratorio de la Universidad por Internet, y realizar las pruebas experimentales.

Opcionalmente, en el caso de tener la plataforma experimental alojada en dos computadores ubicados en lugares separados, se usará una cámara para que el usuario pueda ver los movimientos del robot. El envío de las imágenes provenientes de la cámara, se puede realizar en línea o fuera de línea, dependiendo de los retardos en el canal de comunicaciones con el cual se desee trabajar. En caso de enviarse las imágenes fuera de línea, el usuario podrá observar los movimientos del robot por medio del bloque de la interfaz gráfica implementada para interactuar con simulink.

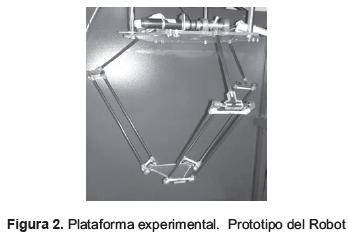
En la figura 2, se muestra el prototipo del robot Delta construido que tiene la característica de que sus eslabones (barras de fibra de vidrio), son intercambiables, con el fin de modificar sus dimensiones.

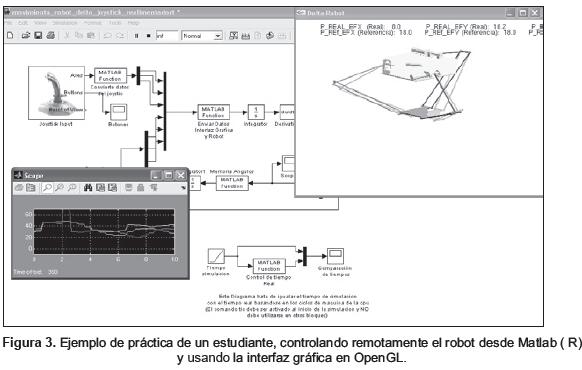
En la figura 3, se ilustra un ejemplo de una práctica realizada por estudiantes, donde el usuario controla el robot de forma remota, y se aprecia: el diagrama de bloques en Simulink ( R), utilizando algoritmos de tiempo real (Soft Real Time - basado en el conteo de ciclos de CPU), y una aplicación desarrollada en OpenGL que permite visualizar el estado del robot real y de las referencias de una forma muy rápida para disminuir el período de los ciclos de funcionamiento del sistema de control.

2. ANÁLISIS CINEMÁTICO DE LA ESTRUCTURA PARALELA

La figura 4(a) muestra el esquema simplificado de un robot tipo Delta, que consiste de dos plataformas: la fija, en donde se ubican los actuadores que para este tipo de robot son motores rotativos, colocados a la misma distancia del centro O, en los puntos 1, 2 y 3, y la plataforma móvil que porta el efector del robot, ubicado en forma adecuada en el centro del triángulo.

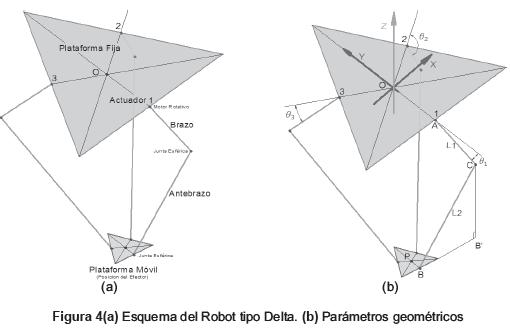
Las dos plataformas están unidas entre sí, por tres estructuras de barras idénticas conformadas por un brazo solidario en cada uno de los motores y por un antebrazo que está unido al brazo y a la plataforma móvil, por medio de juntas esféricas.

El problema cinemático en un robot, es encontrar la relación de la posición del efector final y los ángulos (o posiciones), de los actuadores; en el caso del Robot tipo Delta, el análisis cinemático inverso busca encontrar la relación entre la posición de la plataforma móvil, específicamente el punto P [X₀, Y₀, Z₀], y los ángulos de los brazos θ1, θ2 y θ3 donde están colocados los motores, como se muestra en la figura 4(b). El brazo tiene una longitud L1 y el Antebrazo L2. Se toman los puntos A, B y C, como referencia para el análisis.

Cinemática inversa. Su objetivo es encontrar el ángulo de cada actuador, conociendo la posición del efector final; este problema se produce cuando se tienen las coordenadas de un objeto que se quiere manipular, y se desea saber el ángulo que debe suministrar el sistema de control a cada motor.

Debido a la restricción de la junta A, el brazo describe una circunferencia de radio L1, mientras que con respecto del punto B, el punto antebrazo puede describir una esfera de Radio L2. La intersección de la circunferencia y la esfera se produce en dos puntos, se toma como solución el punto con menor valor en la coordenada Y. Al determinar la posición del punto C, se puede obtener el ángulo 01 del actuador, como se muestra en la figura 5.

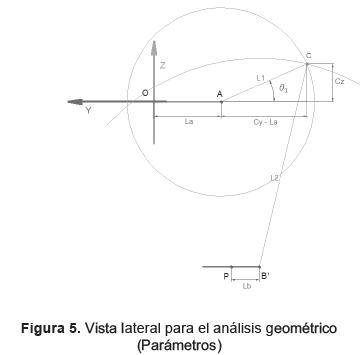
Coordenadas del Punto P, B, A y B'.

Con las coordenadas de los puntos descritos, se plantea un sistema de dos ecuaciones no lineales que permita encontrar la posición del punto C, con la cual se puede calcular el ángulo que forma el brazo con el plano horizontal, y se obteniene así, la solución esperada. Sistema de ecuaciones:

Solucionando este sistema de ecuaciones (1) y (2), se llega a la siguiente ecuación cuadrática (3) que nos sirve para definir la solución.

Donde los valores de a, b y c son:

Cuya solución general es la forma mostrada en la ecuación (7).

Que tiene sentido sólo cuando el argumento de la raíz cuadrada es positivo; de las dos posibles soluciones, se toma la menor de las dos. El valor del ángulo del brazo 1 se calcula con la fórmula (8)

Para los otros brazos, se usa la matriz de rotación con un ángulo de 120° para el brazo 2 y 240° para el 3. Esta matriz de rotación permite girar el sistema de coordenadas, de manera que se pueda usar la solución descrita para el cálculo de los restantes ángulos. Esta solución se validó con una aplicación en Matlab ( R).

3. MODELO DINÁMICO DEL ROBOT TIPO DELTA

Para la evaluación dinámica de la estructura paralela, se usa el modelo dinámico Lagrangiano, en donde los pares de cada motor, se calcula como una función de las masas de las barras, las inercias asociadas con las mismas y las inercias propias de los motores.

Los coeficientes 1, 2 y 3 son los multiplicadores de Lagrange y se obtienen al solucionar el siguiente sistema de ecuaciones.

Donde:

4. VERIFICACIÓN DEL ESPACIO DE TRABAJO IMPUESTO

Los robots paralelos se caracterizan por tener grandes prestaciones en cuanto a velocidad, rigidez, alta relación entre la capacidad de carga y peso del propio robot, lo cual ha impulsado significativamente sus aplicaciones en las últimas décadas. Sin embargo, estos robots presentan una desventaja frente a los robots seriales y en su reducido espacio de trabajo.

El robot paralelo con configuración Delta es muy usado en la industria; por esta razón, se han realizado múltiples investigaciones en cuanto su diseño [12], [13] y [14]. Algunos de los resultados más relevantes radican en sustituir en las articulaciones rotacionales por actuadores lineales [15]. Aunque estas sustituciones producen una ampliación del espacio de trabajo, reducen en forma significativa, la velocidad del efector final, lo cual se debe a que los actuadores lineales no suelen alcanzar velocidades altas. Por esta razón, en este artículo se hace una optimización de la estructura tipo delta sin modificaciones, con el fin de obtener la relación entre los diferentes parámetros dimensionales del robot, manteniendo sus prestaciones de alta velocidad que son las que lo caracterizan.

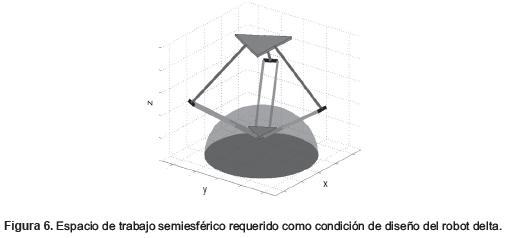
Con el fin de realizar una optimización de las dimensiones del robot se decidió establecer un espacio de trabajo semiesférico, que resultaría muy útil en la mayoría de aplicaciones donde suele utilizarse este tipo de robot. El objetivo consistirá en diseñar un robot que pueda posicionar su efector final en cualquier punto dentro de esta media esfera. En la figura 6, se puede apreciar el robot con el efector final situado en un punto dentro de la semi-esfera.

Además de las comprobaciones matemáticas correspondientes a la cinemática del robot, es necesario corroborar las colisiones del robot en cada uno de los puntos requeridos, con el fin de verificar que el efector final del robot realmente pueda situarse en la posición señalada. En la figura 7, se aprecia un ejemplo de un punto en donde las condiciones matemáticas correspondientes a la cinemática inversa se cumplen; sin embargo, incurre en interferencias entre sus propios eslabones. Si se le pidiese al robot ir a dicho punto, incurriría en una colisión.

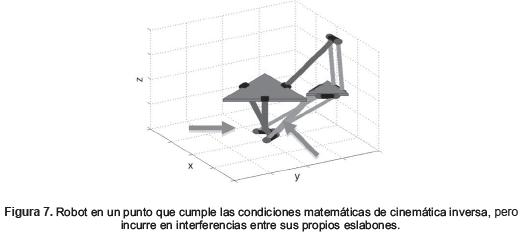
Las dimensiones de los robots que cumplen con las condiciones cinemáticas y no incurren en colisiones en todos los puntos del espacio de trabajo requerido, son seleccionados dentro del conjunto de prototipos aptos para realizar la optimización.

5. OPTIMIZACIÓN DE LAS DIMENSIONES DEL ROBOT

Uno de los objetivos principales de este trabajo, es obtener las dimensiones de un prototipo de robot, de tal forma que consuma la menor cantidad de energía para recorrer una trayectoria dentro del espacio de trabajo común. La idea es que las dimensiones del robot sean las más adecuadas, y consuma la menor cantidad de energía al realizar el recorrido. Esto se hace, teniendo en cuenta los requerimientos actuales de la industrial en los cuales se exige que los productos sean sostenibles {greendesign). Adicionalmente, el robot se construirá en la medida de lo posible, con materiales reciclables y/o no dañinos para el medio ambiente.

La trayectoria consiste en una serie de espirales que cubren puntos significativos dentro del espacio de trabajo, iniciando por el límite exterior del mismo y luego, tomando zonas internas; el tamaño del espacio de trabajo usado es una semi-esfera de una unidad de diámetro que se adecúa a las dimensiones normalizadas del robot.

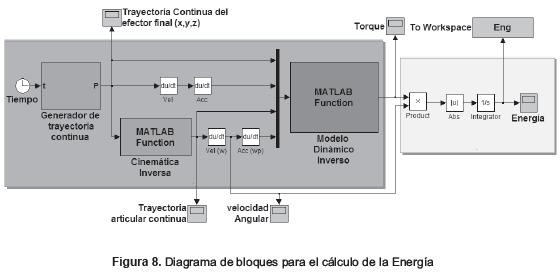
Para obtener la cantidad de energía que usa cada configuración del robot al recorrer la trayectoria prescrita, se desarrolló un modelo en Simulink ( R) que toma los puntos especificados para generar la trayectoria del efector final (posición x, y, z, y tiempo) y por medio de un interpolador de tipo spline cúbico, los algoritmos de cinemática inversa se calculan las trayectorias continuas de las tres articulaciones activas del robot. Utilizando estas trayectorias continuas (incluyen la posición, velocidad y aceleración), y el modelo dinámico inverso, se calculan los pares requeridos en cada articulación para desarrollar las trayectorias planteadas.

Finalmente, los pares se usan junto con la velocidad angular de las articulaciones activas para calcular las curvas de potencia de cada motor. Al realizar la integración de la suma de las potencias, se obtiene la energía que consume el robot para desarrollar la tarea; esta cantidad de energía se usa como valor de referencia para la optimización. En la figura 8, se muestra el diagrama de bloques que realiza el cálculo de la energía.

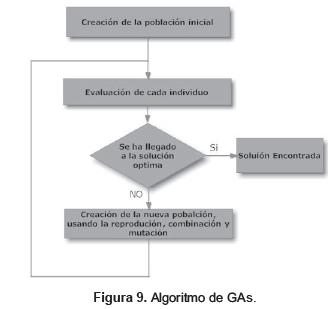
El método usado en la optimización es el de Algoritmos Genéticos (GAs) que se muestra en la figura 9.

Los parámetros usados durante la optimization por algoritmos genéticos, se presentan en la tabla 1.

La función para optimizar, se desarrolló en Matlab ( R); cada individuo tiene cuatro genes que son las dimensiones principales del robot (tamaño de las plataformas, fija y móvil, tamaño del brazo y tamaño del antebrazo), la función de desempeño por minimizar, es la energía (ecuación 15), que se calcula con los programas asociados y el diagrama de bloques que se muestra en la figura 8. Las medidas se normalizaron entre 0 y 1 unidades, de manera que los resultados se puedan extrapolar a cualquier tamaño del robot.

Donde:
- Pares de los motores
- Velocidades angulares de los motores

6. RESULTADOS

Siguiendo el algoritmo de optimización planteado en la sección anterior, se procedió a calcular los valores óptimos de los eslabones del prototipo del robot paralelo y que hacen que la energía para recorrer la trayectoria sea mínima.

El proceso de optimización que se presenta en la figura 10, converge en la generación número 97 después de probar a 4.900 individuos. Los genes del mejor individuo (dimensiones principales del robot), se muestran en la tabla 2.

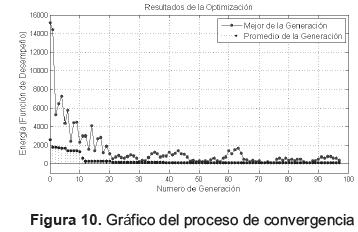
De acuerdo con los resultados, se puede deducir que el tamaño de las plataformas debe ser muy pequeño y la longitud del antebrazo (L₂), debe ser aproximadamente el doble de la longitud del brazo (L₁). Las dimensiones de estos elementos dependerán del espacio de trabajo planteado, tal como se aprecia en la tabla 2.

7. CONCLUSIONES

Los algoritmos genéticos son una herramienta funcional que permite estimar las dimensiones de un robot paralelo tipo Delta con un bajo consumo de energía.

La verificación de cobertura del espacio de trabajo y el análisis de interferencia son elementos clave en el diseño del robot y garantizan la capacidad de recorrer las diversas trayectorias para las cuales se planea el uso del robot.

El diseño de la plataforma remota que contiene el robot paralelo, permitirá a estudiantes de diferentes universidades corroborar experimentalmente diferentes esquemas de control propuestos, que pueden ser sencillos o muy complejos, según como se requiera. El uso de Matlab permitirá que los estudiantes implementen estos esquemas de una forma muy rápida.

El uso de una interfaz gráfica implementada en C, usando librerías OpenGL, reduce en forma significativa los tiempos de ejecución de los algoritmos de control, lo cual es factor relevante en el diseño de sistemas teleoperados.

REFERENCIAS BIBLIOGRAFÍCAS

[1] Baykal S. G., (2010). Green Automation, Automática 2010, International Trade Fair for Automation and Mechatronics.        [ Links ]

[2] Albers, A. and Ottnad, J. (2009). Integrated structural and controller optimization for lightweight robot design. Humanoid Robot 9^th. IEEE-RAS International Conference, pp. 93 -98.        [ Links ]

[3] Bailón W., Cardiel E., Campos I. y Paz A. (2010). Mechanical energy optimization in trajectory planning for six DOF robot manipulators based on eighth-degree polynomial functions and a genetic algorithm. Electrical Engineering Computing Science and Automatic Control (CCE), 7th International Conference, pp. 446 -451.        [ Links ]

[4] Kolibalbal Z., and Smetanova A., (2010). Experimental implementation of energy optimization by robot movement. Robotics in Alpe-Adria-Danube Region (RAAD). IEEE 19th International Workshop, pp. 333 -339.        [ Links ]

[5] Vergnano A., Thorstensson C, Lennartson B., Falkman P., Pellicciari M., Yuan C, Biller S. y Leali F., (2010). Embedding detailed robot energy optimization into high-level scheduling. Automation Science and Engineering (CASE), IEEE Conference, pp. 386 -392.        [ Links ]

[6] Merlet J. P., (2006). Parallel Robots (Solid Mechanics and Its Applications), New York: Springer-Verlag.        [ Links ]

[7] Ranky P.G., (2010). Sustainable green product design and manufacturing / assembly systems engineering principles and rules with examples. Sustainable Systems and Technology (ISSST). IEEE International Symposium.        [ Links ]

[8] Zhi-Gang Xu, Li-Yan Shen, Wen-Guang Chen, (2006). Conceptual Green design, challenge and strategies.Industrial Electronics. IEEE International Symposium.        [ Links ]

[9] Glantschnig W.J., (2002). Green design: an introduction to issues and challenges. Components. Packaging and Manufacturing Technology. Part A, IEEE Transactions.        [ Links ]

[10] Liu X.J., Jin Z.L., and Gao F., (2000). Optimum design of 3-DOF spherical parallel manipulators with respect to the conditioning and stiffness indices In: Mechanism Machine Theory 35, pp. 1257-1267.        [ Links ]

[11] Clavel R., (1989). Une nouvelle structure de manipulateurparalléle pour la robotiquelégére. Journal Européen des SystémesAutomatisés, 23 (6), pp. 501-519.        [ Links ]

[12] Lou Y., Liu G., Chen N., and Li Z., (2005). Optimal design of parallel manipulators for maximum effective regular workspace, Proc. IEEE/RSJ Int. Conf. on Intel. Robots Sys., pp. 795-800. Alberta.        [ Links ]

[13] Qiaoling Yuan, Shiming J.i., Zhongfei Wang, Guan Wang, Yuehua Wan, Li Zhan, (2008). Optimal design of the linear delta robot for prescribed cuboid dexterous workspace based on performance chart. Proceedings of the 8th WSEAS International Conference on Robotics. In: Control and Manufacturing Technology, p.35-41, Hangzhou, China.        [ Links ]

[14] Courteille E., Deblaise D., and Maurine P., (2009). Design optimization of a Delta-like parallel robot through global stiffness performance evaluation. IEEE. In: Intelligent Robots and Systems, 2009. IEEE/RSJ International Conference.        [ Links ]

[15] Stock M., and Miller K., (2003). Optimal design of spatial parallel manipulators: application to linear DELTA robot, In: ASME J. Mech. Des., Vol. 125, pp. 292-301.        [ Links ]