Introduction
This review article presents the application of metaheuristic optimization algorithms in pavement engineering. Optimization is about finding the best solution from a pool that contains all the feasible solutions by following a three-step decision-making process: (a) to know the model or system, (b) to define the system effectiveness or objective function, and (c) to apply the theory of optimization [1]. A previous review on optimization techniques in civil engineering summarized an increasing number of optimization algorithms and their applications to geotechnical, transportation, construction management, hydraulic, structural, and mechanical engineering problems. However, among 147 references, there were only two papers related to pavement engineering [2].
Pavement engineering is a crossroads between geotechnical and transportation engineering with a sound base in construction materials. It is not surprising that there are multiple applications of optimization algorithms in this area, emphasizing pavement management (PM) for its socioeconomic implications and back-calculation of layer properties for its complexity, considering the viscoelastic and nonlinear behavior of the materials.
In the following sections, the authors summarize the research about metaheuristic optimization in pavement management systems (PMS) in the last 25 years and conclude about past, present, and future lines of research. Most of the applications use genetic algorithms whose fundamentals can be found, for the sake of brevity, elsewhere [3].
Applied Optimization in Pavement Management
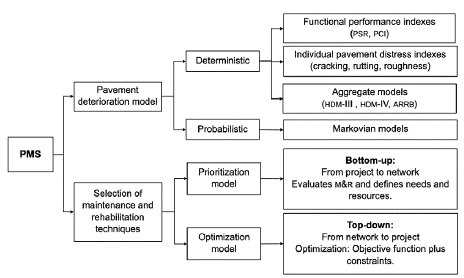
PM systematically involves planning and programming expenditures, design, construction, maintenance, operation, and in-service evaluation of pavement structures in roads, airports, and parking lots. Management activities include data acquisition, planning, programming, new construction, maintenance, rehabilitation, and renovation of pavements [4].
The decision-making process in PM has two basic levels: (a) the network level to develop a priority program and schedule work within a budget, and (b) the project level to focus on a particular location and prioritize the physical implementation of network decisions [5]. PMSS consider multiple objectives like minimizing the discounted total or annual expenditures, maximizing the pavement network condition according to a performance measure, or maximizing the use of workforce and machine resources. In general, there are two types of maintenance and rehabilitation (M&R) scheduling problems in PM: the budget planning problem (minimizing cost over time) and the budget allocation problem (maximizing the effectiveness or minimizing user costs) subjected to budget constraints [6]. Fig. 1 shows the components and activities of a PMS.
PMS evolved into "Asset Management Systems," considering the bridges and other components of the infrastructure and combining engineering principles with business practice and economic theory [8]. Asset management is a process of resource allocation (budget, labor, and facility) in several decision-making levels like asset class (pavement or bridges), category of works (preservation versus a capacity expansion), and projects in each asset class and work category [9].
The need for optimization techniques is evident in the combinatorial double-exponential budget allocation problem on a pavement network, whose search space of possible solutions is defined by eq. (1):
Where S s is the size of the search space for the optimizing problem, A is the number of activities, P s is the number of pavement sections, and T is the analysis period in years. PMSS require a module to optimize maintenance alternatives at the network level to solve this combinatorial problem [10]. Considering four management activities (0: do-nothing, 1: routine maintenance, 2: rehabilitation, and 3: reconstruction) and an analysis period of several years, the number of pavement sections in the network defines the size of the search space for the problem. A pavement section represents similar conditions of climate, traffic, subgrade, materials, and pavement condition. For example, two climatic zones, three levels of traffic, four types of subgrades, two types of pavements, and seven categories of pavement condition define 366xN combinations, where N is the actual number of sections in the pavement network. Sections' longitude range between hundreds to thousands of meters, so their number in a road network is significant. Thus, for a 20-year analysis period, eq. (1) yields possible (4)(366N) 20 combinations of management activities in the network. This "combinatorial explosion" defines an "N-hard" problem, which needs significant computing power [11].
The programming of PMS activities based on ranking methods or subjective priority rules does not guarantee optimal utilization of available resources [12]. At the same time, effective management will produce a safe environment for public users [13].
Metaheuristic Optimization in Pavement Management
A literature review shows multiple optimization techniques applications to the pm problem in the last 25 years. Table 1 summarizes the main characteristics of several applications of genetic algorithms and other soft computing techniques in PMS.
Table 1 Summary of pavement management applications with soft computing
| Reference | Description | Methods (a) | Crossover type and rate (b) | Mutation type and rate (c) | Population range (selected) | Maximum generations |
|---|---|---|---|---|---|---|
| [3] | Road network maintenance | GA and RA | OP | UF-SG (0.10) | 10-80 (50) | 50 |
| [14] | Road network maintenance | GA and RA | OP (0.80) | SG (0.20) | 80 | 100 |
| [15] | Road maintenance based in optimized weights of the ANN | GA and ANN | (0.70) | (0.10) | 10 | 50 |
| [16] | Road network maintenance | GA and RA | OP (0.80) | UF- SG (0.20) | 30 | 100 |
| [12] | PM activities programming | GA | OP (NR) (d) | UF (NR) | NR | NR |
| [11] | Multi-objective optimization in PM | GA and RA | OP (0.60) | UF (0.01) | 60 | 70 |
| [17] | Multi-objective programming of PM activities | GA and RA | OP (0.80) | UF (0.10) | 200 | 500 |
| [18] | Evaluation of pavement deterioration models | GA and RA | OP (NR) | UF (NR) | NR | Up to 9,600 |
| [19] | Constraint handling methods in pavement maintenance programming | GA and RA | TP (NR) | UF (NR) | 100- 400 | 250 |
| [49] | pm optimization model | GA | OP-U (0.85) | UF (0.05) | 1,000 | NR |
| [20] | Multiyear pavement repair scheduling optimization | GA and ES | NR | NR | 40 | Up to 39,000 |
| [21] | Pavement maintenance scheduling for road closure | GA and S | TP (0.80) | UF (0.05) | 4 | 20 |
| [13] | Multiobjective optimization model for Thailand highway network | GA and RA | MP (0.90) | UF (0.045) | 50 | 100 |
| [22] | Maintenance optimization of infrastructure networks | GA and MC | DA (0.50) | DA (0.01) | 50 | 10,000 |
| [23] | Pavement maintenance management | GA and ANN | OP (0.90) | UF (0.001) | 924 | 1,270 |
| [24] | Multilayer pavement maintenance program | GA, RA, and MC | U (0.50) | UF (0.01) | 32 | 50,000 |
| [25] | Network optimization system with multiple objectives | GA, LP, and MC | OP (0.90) | UF (0.01) | 45 | 150 |
| [4] | Highway infrastructure maintenance schedule | GA | OP (0.70) | UF (0.30) | 100 | 200 |
| [39] | Chaos particle swarm optimization applied in pavement maintenance decision | CPSO VS. NSGA-II | -- NR | -- NR | -- NR | 50 50 |
| [26] | Design and management strategies for mixed public-rivate transportation networks | GA | OP (0.75) | UF (0.004) | 100 | 100 |
| [27] | Road pavement performance evaluation | GA and ANN | OP (NR) | 30 | ||
| [40] | PM activities programming | PSO | -- | -- | 15 | 100 |
| [28] | Integrated prioritization and optimization approach for PM | GA | NR (0.85) | NR (0.05) | 300 | nr |
| [4] | Optimum genetic algorithm structure selection | GA and RA | U (0.90) | SG (0.10) | 50 | 500 |
| [31] | Incorporating priority preferences into pavement maintenance programming | GA | OP (0.85) | UF (0.05) | 300 | nr |
| [34] | Advanced PMS | GA | OP (0.80) | UF (0.90) | 100 | 500 |
| [46] | Analysis of PM Activities | GA and RA vs. pso and RA | NR (0.90) | NR (0.005) | 100 | 1,000 |
| [42] | Planning maintenance works in pavements | ACO | -- | -- | 40 ants | 33 tours |
| [7] | Pavement maintenance scheduling | GA | OP (0.60) | UF (0.01) | 500 | 5,000 |
| [35] | Multi-objective optimum analysis of pavement maintenance | GA and MC | NR (0.60) | NR (0.01) | 100 | NR |
| [36] | Optimization of pavement maintenance under overload traffic | GA | NR | NR | NR | 100 |
| [38] | Comparative study of metaheuristic algorithms for road maintenance planning | NSGA II MOPSQ | NR (0.75) NR | NR (0.30) NR | 45 NR | 400 NR |
| [43] | Multi-objective optimization of pavement maintenance | PSO | -- | -- | 100 | 100 |
| [44] | Improved artificial bee colony algorithm for pavement resurfacing problem | ABC | -- | -- | 100 50 foragers 50 onlookers | 5,000 |
| [48] | Pavement M&R scheduling | WCA, AOA DE, ACO PSO, GA | NR | NR | NR | NR |
Methods: GA: Genetic algorithm, RA: Regression analysis, ANN: Artificial neural network, s: Simulation, ES: Expert system, MC: Markov-chain, LP: Linear programming, PSO: Particle-swarm optimization, ACO: Ant colony optimization, CPSO: Chaos particle swarm optimization, NSGA-II: Non-dominated sorted genetic algorithm, ABC: Artificial Bee Colony, WCA: Water Cycle Algorithm. AOA: Arithmetic Optimization Algorithm. DE: Differential Evolutionary, MOPSO: Multi-objective particle-swarm optimization.
Crossover type: op: One-point, TP: Two-point, u: Uniform, MP: Multi-point, DA: Dynamically adjusted by the software.
Mutation type: UF: Uniform flipping, so: Switching genes, DA: Dynamically adjusted by the software.
Other: NR: Non-reported.
Source: Modified from Golroo and Tighe [4].
The following paragraphs present research based on genetic algorithms and other metaheuris-tics techniques described in Table 1.
Optimization with genetic algorithms
Chan et al. [3] developed the pioneer computer program PAVENET, adapting the genetic algorithm for analyzing the road maintenance management problem at the network level. The objective functions minimized the present worth of the maintenance costs over the planning horizon, maximized the usage of the yearly allocated budgets, or minimized the fluctuations of the annual expenditures. The program did not consider any significant rehabilitation within the analysis period and predicted pavement conditions with deterministic closed-form equations for cracking, rutting, and surface disintegration.
Fwa et al. [14] presented an application of the previous work. The objective function maximized the management activities subjected to production requirements, budget constraints, workforce availability, equipment availability, material availability, and rehabilitation constraints. The case study considered four highway types, four pavement repair activities, and three need-urgency levels considering the number of workdays in a month.
Taha and Hanna [15] introduced a genetic algorithm approach that evolves a neural network model to select the optimum maintenance strategy for flexible pavements from a series of if-then-else rules contained in an expert system. The input factors considered distress type, distress density, a riding condition index, traffic volume, crack type, and distress severity. The genetic algorithm improved the selection of artificial neural network parameters based on the ANN performance in unseen cases (outside the network training database).
Fwa et al. [16] improved the PAVENET-R program to apply genetic algorithms in the programming of pavement M&R activities of a road network over a multiple-period planning horizon. The model considered the division of the network in uniform segments, the definition of a planning period, and the implementation of warning levels and prediction models for cracking, rutting, and surface disintegration based on the AASHTO performance algorithm for flexible pavements. The program considered three maintenance alternatives and one rehabilitation option. The objective function minimized the total present cost, constrained to the relationship between the costs of the overlay rehabilitation and the combination of the maintenance activities and the feasibility of the combined alternatives.
Pilson et al. [11] considered a multi-objective optimization and applied an interactivity model to predict pavement deterioration. The multi-objective function considered both costs and a performance level of pavement and defines an "efficient" frontier (actually, a Pareto front), which may become a hypersurface with additional objective functions. The authors estimated the pavement deterioration with a linear-regression interactivity model that related material conditions in four-layer asphalt pavement. A numerical example showed that it was possible to obtain efficient (Pareto) network surfaces considering two objectives, including penalties for unfeasible individuals.
Fwa et al. [17] developed a genetic algorithm-based formulation for multi-objective programming of PM activities. The authors reviewed the problems from previous publications considering two and three objective functions to identify a Pareto front. The original objective function maximized the labor in total workday units in pavement maintenance while other objective functions considered: (a) minimization of the total maintenance cost and (b) maximization of overall network pavement condition. The final solution selection may consider the expected budget level or any other form of weighting between criteria.
Shekharan [18] used genetic algorithms to evaluate five pavement deterioration models from synthetic databases created from multiple regression models. Deterioration models are essential in the PMS to estimate the evolution of pavement conditions in the analysis period and trigger the warrants for prescribing treatments or rehabilitation procedures. The deterioration models were the present serviceability rating (PSR), the distress maintenance rating (DMR), the pavement condition rating (PCR), and the Texan punchouts and patches model. The objective function minimized the errors between the database and the models based on genetic algorithms.
Chan et al. [19] reviewed the performance of two constraint handling methods and proposed a new way for applying genetic algorithms to pavement maintenance programming at the network level. The authors analyzed a previously published example with an objective function to maximize the total weighted work production under production requirements, budget, workforce, equipment, materials, and rehabilitation constraints. The authors summarized three constraint handling methods' main features and developed the "prioritized resource allocation method" (PRAM), which encodes the value decision variables with additional information about the available resources and always satisfies the resource constraints.
Sundin and Braban-Ledoux [5] did a comprehensive review of artificial intelligence-based decision-support technologies in PM. The primary decision-support technologies for unstructured problems are (a) group support systems, (b) executive information analysis, (c) expert or knowledge-based systems, (d) artificial neural networks, and (e) hybrid support systems. PMSS use deterministic (regression), probabilistic (usually Markovian), or mechanistic-empirical performance prediction models. Fig. 2 shows the applications of Al-based decision-support technologies to the PMS decision-making process with some examples.

Source: Modified after Sundin and Braban-Ledoux [5].
Fig. 2 Al-based decision-support technologies in PMS. Applied Metaheuristic Optimization in Asphalt Pavement Management
Tack and Chou [20] compared the results of simple and constrained genetic algorithms with dynamic programming in multiyear pavement repair scheduling. The objective function maximized the overall average yearly network condition. The constrained genetic algorithm included an expert system in determining the type of repair to individual pavement sections according to their condition. A case study showed that the pre-constrained genetic algorithm achieved an optimum solution faster than the simple genetic algorithm; however, dynamic programming was the most accurate optimization technique.
Cheu et al. [21] presented a hybrid methodology using a genetic algorithm as a search technique coupled with a microscopic traffic simulation model to optimize the daily lane closure scheduling in a network for maintenance activities. The objective function minimized the total travel time of vehicles in the network during the day.
Flintsch and Chen [8] reviewed soft computing applications for infrastructure management. The authors summarized applications of artificial neural networks, fuzzy logic systems, genetic algorithms, and their hybridization for three main tasks in PM: (1) asset performance, (2) needs analysis and, (3) tradeoff analysis. The authors identified applications of genetic algorithms and fuzzy mathematical programming for the latter. The hybridization offered good perspectives; however, the authors identified several issues for soft-computing implementation like legacy systems, lack of understanding of the techniques and their benefits, and lack of data to develop reliable models.
Morcous and Lounis [22] presented an approach that uses a genetic algorithm with Markov-chain models for programming pavement maintenance alternatives. Pavement deterioration is a stochastic process where the probability of a future state depends only on the present state. The maintenance alternatives defined transition probability matrices for the analysis period with associated discounted costs. The objective function minimized the discounted present value of the maintenance costs of all facility groups while keeping the condition of every group at any time above a threshold value.
Herabat and Tangphaisankun [13] developed a multi-objective optimization model to support decision-making and provide optimal maintenance programs to the Thailand highway agency. The authors considered two objective functions: (a) the minimization of vehicle operating costs and (b) the maximization of the road network condition measured by the International Roughness Index (IRI). Also, they computed the operation costs for each type of vehicle, considering the pavement roughness with the HDM-III model, and used five maintenance types with closed-form equations to predict their impact on pavement roughness and a roughness degradation model with time. The constraints included budget limitation (hard constraint) and system preservation based on IRI (soft constraint). The authors found an optimum IRI of 2.702 m/km to trigger maintenance applications.
Bosurgi and Trifirô [23] proposed an optimization procedure for the management of resurfacing interventions on flexible pavements with genetic algorithms based on two indicators: (a) the Side-way Force Coefficient (SFC) and (b) predicted accidents. Both the SFC and the accident prediction models used artificial neural networks related to SFC variation with time, cumulative traffic, geometric and environmental characteristics, and the number of accidents on the road.
Chootinan et al. [24] developed a pavement maintenance program based on the Markov transition probability matrix (TPM) approach to address the uncertainty of the predicted pavement condition. The authors considered the challenge to develop a long-term maintenance plan at the project level that is consistent with the network-level recommendations and considered two objective functions: (a) to minimize the maintenance cost and (b) to maximize the pavement performance. The pavement performance prediction of a pavement section considered an AASHTO-based serviceability rating (PSR) as a function of the initial condition, pavement structural number, age of pavement, cumulative 18-kip axle loads at the specific year, and an adjustment climatic and functional factor. The authors combine the genetic algorithm with the condition simulation to solve the stochastic maintenance problem subjected to budget constraints. The comparison between deterministic and stochastic simulations showed a faster convergence of the latter.
Wang et al. [25] reviewed the Arizona State experience with the Network Optimization System (NOS) based on Markovian transition prediction models of pavement condition prediction coupled with linear optimization. The authors proposed integrating a genetic algorithm to solve the network optimization problem at the network level. NOS considered three pavement factors to establish the pavement condition and generate decision variables: level of roughness, level of cracking, and index to first crack. Also, the system considers six preserving actions from routine maintenance to overlay construction. The objective function maximized the pavement condition while minimizing agency costs in a combined weighted fitness function.
Unnikrishnan et al. [26] proposed a multi-objective bi-level mathematical programming framework to evaluate the impact of M&R in Build-Operate-Transfer (BOT) highways, integrating maintenance and capacity improvements decisions with optimal toll pricing. The users select their routes with the user equilibrium assignment based on time travel, the toll, and the state of the pavement. The private operator and the public agency had different objective functions, maximizing the net present value of the BOT, and minimizing the system's total cost, respectively. A case study on a small network with BOT and public roads showed different Pareto fronts for several combinations of actions from the private and public actors.
Qian [27] improved several performance prediction models for pavements by hybridizing a genetic algorithm and an artificial neural network. The author implemented the genetic algorithm into the back-propagation neural network training with an objective function to minimize the error between observed and predicted pavement performance. A comparison between ANN and GA-ANN showed better forecasts for the hybrid approach.
Javed [28] stated that traditional PM prioritizes rules like "worst goes first," the effective cost, or based on a distress index without a clear physical meaning. A genetic algorithm allowed to maximize the pavement behavior under constrained budget conditions and mitigated the sub-optimal alternatives produced by the user's priority preferences employed in the PMS.
Santos and Ferreira [29] developed OPTIPAV software with genetic algorithms. The program considers the optimization of pavement behavior, the costs of construction, preventive maintenance activities (and rehabilitation), the user costs, and the residual value of the pavement for a given analysis period. The program uses the 1993 AASHTO algorithm and the present serviceability index [30]. The objective function minimized the total discounted costs over the project analysis period while keeping the pavement above specified quality standards. The constraints corresponded to the pavement condition in each year based on the previous state and M&R activities.
Golroo and Tighe [4] reviewed the optimum genetic algorithm structure for developing a maintenance system by performing a sensitivity analysis on the outcome of the problem concerning the genetic algorithm structure. The authors selected five objective functions: (a) minimization of maintenance costs, (b) maximization of saving in vehicle operation cost (voc), (c) maximization of effectiveness, (d) maximization of saving voc over maintenance costs, and (e) maximization of effectiveness over cost. "Effectiveness" is the area under the performance curve multiplied by the length of a pavement section and the annual average daily traffic. The authors recommended evaluating the GA operators instead of using typical values from previous publications in any optimization problem.
Farhan and Fwa [31] examined the implications of a priori application of priority weights in the pavement maintenance programming analysis. Highway agencies apply priority weights according to pavement distress, pavement condition, road class, or traffic volume in the process of optimal programming of pavement maintenance or rehabilitation activities. However, most agencies may ignore the effect that these relative magnitudes have on the optimization process. The authors applied several combinations of priority weights to a case study based on genetic algorithms and found that such values define sub-optimal solutions, the worst for multiple priority weights.
Meneses [32], [33] developed the Multi-objective Decision-Aid Tool (MODAT), a modified version of the OPTIPAV program, to minimize the cost in a planning period by closing the gap between network and project management by changing the standard design variables (thickness, moduli, weather, or traffic) for the damage characterization and its future prediction. The multiple objectives included minimizing the maintenance, rehabilitation, and user costs and maximizing the residual value of the pavement. Constraints have structural and functional characteristics.
Di Mino et al. [34] developed a two-objective optimization model to minimize road accident risk and rehabilitation costs on network and project levels. The authors modeled the pavement deterioration as a Markovian process, used a genetic algorithm to optimize the rehabilitation activities on the pavement, and considered the potential of including a third objective function to minimize user costs.
Elhadidy et al. [35] developed an integrated PMS for the Egyptian road network. The authors implemented a genetic algorithm with a Markov-chain deterioration model considering the available budget and road network condition based on the pavement condition index (PCI). The objective function considered two aspects: (a) minimizing the M&R costs and (b) maximizing the pavement condition. A numerical example showed a clear Pareto front for Egyptian conditions for network and project management.
Yang et al. [7] proposed a new PMS integrating a pavement age gain model to evaluate pavement conditions and NSGA-II to optimize pavement maintenance. The authors assessed both deterministic and probabilistic pavement age models, being the latter more realistic. The objective functions minimized the pavement maintenance cost and maximized the remaining pavement life. The authors defined the parameters of the GA through trial and error. Both deterministic and probabilistic approaches showed clear Pareto fronts with a better result for the stochastic approach because it improved the pavement condition after maintenance. In contrast, the deterministic approach always caused a reduction in the pavement condition.
Rifai et al. [36] developed a two-objective optimization model with GA considering maximum roughness and minimum maintenance cost for in-service road networks subjected to overloading in West Java. The pavement deterioration model forecasts the IRI using Support Vector Machines for highways with and without overloading. The case study achieved both objective functions according to a Pareto analysis considering three levels of loading/overloading.
Santos et al. [37] presented an adaptive hybrid genetic algorithm (AHGA) for PM. The authors combined a genetic algorithm (GA) with local search (LS) mechanisms for solving the pavement M&R strategy selection problem based on the OPTIPAV model. The partial local search mechanism aims to either accelerate the discovery of reasonable solutions or reach solutions that would be unreachable by evolution or a local method alone.
Matin et al. [38] did a comparative study of metaheuristic algorithms for road maintenance planning with a field study in the rural transportation network in Iran. The authors compared both single-objective and multi-objective optimizations with genetic algorithms and particle swarm optimization. The objective functions were: (a) pavement performance maximization and (b) maintenance cost minimization constrained by budget. The pavement performance model was a quadratic regression equation of PCI versus the age of the pavement. The M&R actions included localized preventive, global preventive, and significant maintenance. The authors conclude that multi-objective optimization is better than single-objective optimization.
Optimization with swarm intelligence
Shen et al. [39] applied chaos particle swarm optimization (CPSO), with local solid searching capability and control of population diversity, to pavement maintenance decisions. The objective function maximized the economic benefit and to keep the pavement in an optimal state constrained to the available budget and workforce. A case study against an NSGA-II showed the validity of the CPSO results and faster convergence.
Tayebi [40] applied particle swarm optimization (PSO) to PM activities programming to determine the best M&R activities based on four minimizing cost equations. A replication of the case study proposed by Fwa et al. [16] showed promising results.
Chang [41] applied the PSO method to prioritize pavement sections for M&R activities in the Smooth Roads Project in Taiwan. The pavement condition for 135 pavement sections considered the standard deviation for roughness, rutting, deflections, cracking, pothole, bleeding, patching, and shoving.
Terzi and Serin [42] applied the ant colony optimization (ACO) to the programming of M&R of pavements concerning the budget. The authors proposed a case study to maximize the routine maintenance workload subjected to budget and resource constraints for four classes of highways, four maintenance activities, and three emergency levels. The optimization results were satisfactory compared to the original case study and included a newly implemented budget restriction.
Ahmed et al. [43] applied chaos with discrete multi-objective particle swarm optimization to pavement maintenance. The authors considered two objective functions: minimizing the treatment cost and the sum of all residual PCI values. The "residual pavement condition index" of a pavement section is the subtraction of the existing PCI from 100, multiplied by the annual average daily traffic and the areas of the section as weighting values. The authors estimate the actual PCI with a regression equation considering cracking areas and lengths, pavement age, and maintenance effect. A small case study with five pavement sections, five alternatives of M&R, and a ten-year period showed significant reductions in computing time compared with published solutions.
Panda and Swamy [44] developed an improved artificial bee colony algorithm for the pavement resurfacing problem. The methodology considers user and agency costs, inflation and interest rates, and reachable roughness levels during pavement resurfacing cycles. The solution yields the frequency and thickness of resurfacing, maximizing the cost-effectiveness without the specification of trigger roughness level. The authors used multiple colonies to enhance the exploration and exploitation capabilities of the algorithm.
Optimization with genetic programming
Chang and Chao [45] used genetic programming (GP) to support pavement M&R decisions. The authors conducted GP to explore the M&R decision model between 18 pavement distress types (inputs) and the required M&R treatment among four options (output) based on 2,340 records of pavement distress surveys from seven roads in Taiwan. Global and major M&R activities had the worst accuracies due to their low number of cases in the database. Consequently, the model and algorithm are promising but require further refinement with additional data.
Optimization with greedy search
Yepes et al. [10] developed an optimization module based on local search heuristics to optimize the allocation of maintenance funds at the network level subjected to budgetary and technical restrictions. The heuristic consisted of a hybrid algorithm based on a Greedy Randomized Adaptive Search Procedure (GRASP) to construct a population of feasible solutions considering penalty functions and a Threshold Acceptance (TA) as a postprocessor of the completed solutions to intensify the search. The problem involved a single-objective optimization of the long-term effectiveness based on the area bound by the treatment time versus the performance curve. The performance was a simplified form of the Pavement Condition Index for urban pavements.
Optimization with hybrid methods
Tayebi et al. [46] compared a genetic algorithm with a particle swarm optimization to minimize the cost of PM activities. The authors recognized the complexity of predicting pavement performance and adopted three AAsHto-based distress models: cracking, rutting, and surface disintegration as traffic functions and the pavement structural number (SN). The objective function in both algorithms minimized the M&R activities cost at the network level. The authors found that PSO is an efficient, easy-to-implement optimization model for PMS, even faster and more accurate than the GA.
Nik et al. [47] tested eight hybridizations of PSO and GA to optimize the homogeneous sectioning of a pavement network minimizing the cost and sectioning error on branches and networks based on PCI surveys. The hybrid approach proved to be better than the individual application of PSO and GA, including computing cost.
Naseri et al. [48] evaluated several meta-heuristic algorithms to solve large-scale pavement network M&R scheduling based on the IRI deterioration. A case study with 109 pavement sections indicated that the Water Cycle Algorithm (WCA) has a better performance than genetic algorithms (GA), particle swarm optimization (PSO), and differential evolutionary (DE) methods. However, the authors do not report multiple runs that may yield a different conclusion in this single aspect, considering the random features of metaheuristics.
Conclusions
Metaheuristic methods are powerful tools to optimize PM activities, especially for multi-objective problems such as minimizing costs and maximizing the pavement condition at the network and project levels. According to the reviewed applications, there are three general types of objective functions:
Based on cost or expenditures as follows: (a) minimization of maintenance costs or fluctuations of yearly demand for pavement expenditures, (b) maximization of usage of the allocated budget, and (c) maximization of savings in vehicle operating costs.
Based on resource consumption as follows: (a) maximization of usage of available workforce or minimization of workforce requirements, (b) maximization of usage of available equipment or minimization of equipment requirements, and (c) maximization of maintenance production.
Based on pavement condition or network operation as follows: (a) maximization of effectiveness, (b) maximization of overall network pavement condition, (c) maximization of skid resistance, (d) minimization of total travel time of vehicles in a network under maintenance, and (e) minimization of accidents. Cost-based functions are the preferred objective functions or constraints (fixed budget). Resource consumption-based objective functions are of interest to highway agencies with in-house capabilities beyond administrative management (self construction). Pavement condition-based is the most comprehensive objective function because it can be directly related to agency and user costs (vehicle operation costs, delay of users, and cost of accidents).
Beyond the promising published case studies in the last 25 years, one must consider testing new metaheuristic applications on minor test problems to compare their results to global optimum solutions obtained through complete enumeration [49]. Most of the reviewed applications used small-size numerical cases with pavement networks composed of less than 100 homogeneous sections with longitudes near 500 meters. Also, typical pavement sections may provide a programming scheme, but further work is necessary to execute the PMS activities on individual pavement sections.
Many examples apply genetic algorithms, and it would be wise to implement parallelization techniques to expand the problem sizes beyond the typical cases with some pavement sections and a handful of management activities [50]. PM is a heavily constrained problem, and the random generation of individuals may produce a high rate of invalid agents in genetic algorithms. Although the penalty or "decode & repair" methods are preferred to deal with invalid individuals, it is convenient to consider the constraints in encoding solutions or using a free-encoding algorithm like particle swarm optimization. The genetic algorithm performance improves significantly with hybridization with expert systems to reduce invalid individuals' production or parallelization with subset migration among populations. Recent research by Alqaili et al. [51] presents a multi-objective stochastic algorithm for discrete variables (ISA), which surpasses the genetic algorithm in improving the PCR based on IRI of a pavement network with a minimum budget in developing countries.
Multi-objective optimization is fundamental for better implementing PM activities because it explores a set of near-optimum solutions that offer tradeoffs for the highway agency. The current efforts in multi-objective optimization focus on two or three objective functions. Mathematically, it is possible to define N objective functions and obtain an incumbent solution with the minimum vector from the origin to the normalized N-dimensional Pareto hyper-front. However, the current research and technology transfer state demands a simple approach to mitigate the resistance to embrace this new analysis method.
Future research in multi-objective optimization calls for sustainable aspects, such as environmental and social impacts, to assess the overall costs and benefits induced by maintenance alternatives [10]. Wu et al. [9] reviewed the application of multi-objective optimization techniques at strategic (cross-asset), network, and project levels of highway asset management and highlighted the advantages of multi-objective optimization techniques over traditional approaches. The authors described several methods used for supporting infrastructure management decisions considering multiple objectives. No single multi-objective optimization technique is superior, and the applicability depends on the conditions for the problem and available information.
Finally, one must take into account the stochastic process of pavement deterioration with Markov-chain models as proposed in the Arizona State PMS [49] or by Morcous and Lounis [22] and Shahin [52] for the PCI prediction. Prediction models are improving at a fast-paced rhythm thanks to machine learning methods hybridized with metaheuristics to forecast the pavement condition from structure-related data, for example, the labor-intensive pavement condition index from falling weight deflectometer measurements. Once calibrated, the prediction model evaluates multiple M&R scheme alternatives to maximize the pavement condition with the lowest cost [53]. Machine learning also allows to predict the IRI based on large amounts of data, for example, the Long-Term Pavement Performance dataset [54], and assess vehicle operating costs [55] as part of an optimization plan.