Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ecos de Economía
Print version ISSN 1657-4206
ecos.econ. vol.15 no.33 Medellín July/Dec. 2011
ARTÍCULO DE INVESTIGACIÓN
Infraestructura pública y precios de vivienda: una aplicación de regresión geográficamente ponderada en el contexto de precios hedónicos
Public infrastructure and housing prices: An application of geographically weighted regression within the context of hedonic prices
Juan Carlos Duque*, Hermilson Velásquez**, Jorge Agudelo***
* PhD en estudios empresariales. Research in SpatialEconomics (RISE-group), Department of Economics, Universidad EAFIT. Correo electrónico: jduquec1@eafit.edu.co
** PhD en matemáticas. Research in Spatial Economics (RISE-group), Department of Fundamental Sciences, Universidad EAFIT. Correo electrónico: evelas@eafit.edu.co
*** Grado de escolaridad: Master en Economía. Filiación institucional: Research in Spatial Economics (RISE-group), Department of Economics, Universidad EAFIT. Correo electrónico: agudelotorres@hotmail.com
Fecha de recepción: 10/06/2011 Fecha de aprobación: 11/17/2011
Resumen
El análisis de las externalidades en el sector inmobiliario ha atraído desde hace varios años la atención de los investigadores suscitando una gran cantidad de estudios al respecto. En este artículo se utilizan modelos econométricos tradicionales, de la econometría espacial y de regresión ponderada geográficamente, para analizar y comparar a la luz de estos modelos la influencia que tiene en los precios de las viviendas la existencia de una estación del metro en San Javier ubicada en el centro occidente de la ciudad de Medel ín.
El principal hal azgo en este estudio es que la presencia de la estación del metro tiene una influencia positiva en los precios de las viviendas localizadas en un radio de 600 metros alrededor de la estación; sin embargo, las viviendas cercanas a las vías de acceso del metro a la estación presentan un importante decremento en sus precios.
Palabras clave Sector Inmobiliario, GWR, Regresión Geográficamente Ponderada, Metro de Medellín, Precios hedónicos.
Abstract
The analysis of externalities in real state has been matter of study during the past few years. In this paper we use both conventional and spatial econometric model, as wel as geographical y weighted regression models, to measure the effect of the San Javier Metro Station (in Medel ín, Colombia) on the housing prices of the surrounding area.
The main finding of this study is that the metro station has a positive impact on the prices of houses located within a radius of 600 meter from the station. However, the railroad track accessing the station has a negative impact on housing prices located nearby
Key words Real state, GWR, Geographical y Weighted Regression, Hedonic prices, Metro station.
Introducción
El comportamiento del sector inmobiliario ha sido estudiado desde hace más de sesenta años. En el siglo pasado, los trabajos pioneros sobre propiedad raíz estaban enfocados a explicar que la propiedad raíz era una buena inversión dadas las rentas que producía mensualmente y el crecimiento de precio de los inmuebles (Dewey y DeTuro, 1950; Thomson, 1950; Beaty, 1952). Posteriormente en los primeros años de la década del setenta, la atención se centró en los modelos de precios hedónicos que reflejaban la interacción entre la oferta y la demanda del mercado, a través de especificaciones en las que se establecían relaciones funcionales entre las características de los bienes, y los precios de venta de los mismos (Rosen, 1974). En las décadas siguientes, entre los años ochenta y noventa, algunos autores consideraron como factores determinantes en la explicación del precio de la vivienda de factores externos como el vecindario, la cercanía a algún lugar importante o una vista agradable, información que se introducía en la especificación de un modelo econométrico tradicional mediante variables dummy para indicar la existencia externalidades que afectan el precio de las viviendas (French y Lafferty, 1984; Dubin y Goodman ,1982; Portney, 1981; Quang Do y Grudnistski, 1995; Carroll, Clauretie y Jensen, 1996).
En los modelos de precios hedónicos, se consideran como determinantes del precio de la vivienda las características de la misma. Esto hace particularmente importantes los problemas de especificación del modelo relacionados con la omisión de variables relevantes o los ligados a la fuerte correlación entre las mismas. Por tal motivo autores como Can (1992) agruparon las especificaciones de las viviendas en ítems como características estructurales, características del vecindario y fecha en la que se recogieron los datos. Otros autores como Basu y Thibodeau (1998) discriminaron las características de las viviendas en siete ítems: las asociadas al lote, a las mejoras, la accesibilidad, la proximidad de externalidades, uso de la tierra y época en la que se recolectan los datos. Todo esto con el fin de evitar sesgos de especificación o de omisión de variables relevantes.
Precio = f (Características estructurales, Características del vecindario, fecha)
La metodología econométrica tradicional utilizada comúnmente no tiene en cuenta la correlación espacial de los datos, es decir, se omite el espacio como fuente de variabilidad de los datos. Y en segundo lugar, no tiene en cuenta la heterogeneidad espacial de los datos, lo que implica que los valores de los parámetros pueden variar en el espacio (Anselin, 1988). Estos aspectos llegan a representar un gran problema debido a que la econometría arroja parámetros que son promedios obtenidos a partir de los datos y no reflejan de modo alguno la variabilidad o la asociación espacial de los datos empleados.
Fundamentación Económica
Desde una perspectiva económica, los modelos de precios hedónicos que son aquel os en los cuales el precio de un bien está determinado por sus características, comenzaron a gestarse a mediados del siglo pasado en la década del sesenta, cuando Lancaster (1966) propuso lo que llamó una ''nueva aproximación a la teoría del consumidor'', en la cual consideró que la utilidad de los bienes era derivada de sus características, rompiendo con la idea de que venía dada implícitamente en ellos. Este enfoque contó con tres ideas principales: En primer lugar asumió que cada bien posee un conjunto de características que son las que dan la utilidad al mismo. En segundo lugar, definió que un bien posee más de una característica y muchas características son compartidas por más de un bien. Por último, los bienes en combinación debían tener diferentes características que perteneciesen a los bienes separadamente. De esta manera comenzó a gestarse una nueva aproximación a la teoría del consumidor a través del estudio de los modelos de precios hedónicos.
El problema consiste en que los consumidores derivan una utilidad del consumo de un bien definido por un vector Z de J características diferentes, más el consumo de un bien compuesto Y. Los consumidores tienen un ingreso fijo M y consideran una función de precios P(Z) que les da el precio del bien heterogéneo como una función de las características Z del bien y un vector de parámetros observados y no observados que caracteriza las preferencias de las familias denotado por α . Las preferencias son representadas por la función de utilidad
u = u (Z, Y α)
De la función de utilidad puede derivarse el monto que la familia estaría dispuesta a pagar por un bien como una función de sus características, dados el ingreso y el nivel de utilidad de la familia. Esta familia tiene una función de renta de alquiler definida por β (Z, M, u, α), entonces la función de utilidad es:
u = u (Z, M - β, α)
La derivada de esta función da la tasa a la cual la familia podría permitirse gastar en un bien cuya característica i se incrementa, mientras se mantiene constante el nivel de utilidad. La familia escoge un bien con características Z, y consume de un bien compuesto Y, para resolver:

La restricción implica que el ingreso de las familias se distribuye entre la compra de un bien compuesto Y y bienes heterogéneos representados por la función de precios P(Z).
Sea λ el multiplicador de lagrange asociado a la restricción, el lagrangiano para este problema de optimización esta dado por:
l = u (Z, M - β, α) + α [M - (P (Z) + Y)]
Las condiciones de primer orden son:

P(Z) es la función de precios hedónicos y hace  referencia usualmente al precio hedónico de una característica. La solución de este problema muestra que la elección óptima de un bien está caracterizada por la igualdad entre el intercepto de la oferta de renta y el precio hedónico de cada característica:
referencia usualmente al precio hedónico de una característica. La solución de este problema muestra que la elección óptima de un bien está caracterizada por la igualdad entre el intercepto de la oferta de renta y el precio hedónico de cada característica:
Esta condición de igualdad es parte de la justificación de la aproximación hedónica al análisis de mercados, para el o indicamos que si podemos observar o estimar el precio hedónico de una característica y una elección hecha por el consumidor, entonces bajo la asunción de conducta optimizadora, la observación provee información local acerca de las preferencias o la disposición a pagar por los atributos. En este sentido el problema parece similar al del análisis estándar de la conducta del consumidor, en el cual las elecciones observadas y los precios proveen información acerca de las preferencias de los consumidores y dan suficientes datos que se espera den inferencias acerca de la conducta del consumidor y la determinación de precios.
Años más tarde Rosen (1974) continuando con la línea de Lancaster (1966) definió como conjunto de precios hedónicos al vínculo existente entre los precios de los bienes y las características de los mismos, estableciendo relaciones funcionales entre ambos. A partir de esta teoría formuló el problema de mercado como un problema de equilibrio espacial en el que tanto los consumidores como los productores toman decisiones en el espacio respecto a un bien que cuenta con características estructurales y espaciales definidas. De esta manera comenzó la búsqueda de relaciones funcionales entre las características de los bienes y los precios.
Algunas décadas después, durante los años ochenta y noventa, los modelos de precios hedónicos empezaron a utilizarse frecuentemente en el sector inmobiliario, particularmente en el área de precios de inmuebles, siendo el trabajo de Can (1992) uno de los pioneros en la estandarización de las características de las viviendas al dividirlas en dos grupos: uno asociado a las características estructurales como tamaño del lote, de la construcción y edad de la vivienda y el otro asociado a las características del vecindario como uso del suelo y externalidades.
Sin embargo, la implementación de los modelos de precios hedónicos en el área de precios de vivienda,se desarrolló frecuentemente aplicando la metodología econométrica tradicional a datos de naturaleza espacial, lo que atrajo dos tipos de problemas (Anselin, 1988): El primero, asociado a la correlación espacial que se presenta cuando hay niveles de dependencia espacial entre las variables, lo cual es particularmente válido en el mercado inmobiliario en el que las viviendas de mayor y menor precio tienden a estar aglomeradas en lugares específicos. El segundo, relacionado con la heterogeneidad espacial, según la cual los parámetros y las formas funcionales varían de acuerdo con la localización de los datos, es decir, los coeficientes obtenidos en el modelo son inestables en el espacio. Esto es particularmente válido en caso del mercado inmobiliario, en el cual una característica de un inmueble, puede ser de vital importancia en una zona con nivel económico alto y no serlo en una zona de estrato bajo, como por ejemplo un parqueadero.
En este contexto de dependencia y heterogeneidad espacial de los datos del mercado de vivienda, surge la técnica GWR que considera explícitamente este tipo de fenómenos al permitir la existencia de coeficientes de regresión que varían en el espacio. En tal sentido, GWR permite construir modelos en los cuales se puede incorporar la heterogeneidad y la dependencia espacial presente en el mercado inmobiliario. Un ejemplo de el o son los vecindarios en los que existen mezclas de casas antiguas, de grandes áreas y precios elevados, con apartamentos nuevos, de áreas menores y precios relativamente más bajos. En este caso la metodología econométrica tradicional arroja coeficientes que son promedios de los datos, mientras que GWR arroja coeficientes ponderados de cada una de las características, entregando una mayor información de la realidad del mercado.
En el contexto de precios de vivienda, se han realizado pocos estudios en ciudades de países que cuentan con mayor flujo de información. Bitter, Mulligan y Dall'erba (2006) en la cual realizaron una comparación entre los métodos de expansión y GWR, mediante un análisis de más de once mil datos de ventas del mercado inmobiliario en Tucson. Para el o especificaron modelos en los que como variable dependiente fue empleado el precio de venta y como independientes el área construida, el área del lote, la calidad de la vivienda, la historia de la vivienda y la edad de la misma, con los cuales especificaron varios modelos empleando distintos tipos de técnicas. Los resultados mostraron que todas las variables empleadas eran significativas y que los precios marginales de los atributos de las viviendas eran variables en el espacio. Por tanto la técnica GWR fue superior al método de expansión en términos de poder explicativo y exactitud de la estimación.
Una aplicación similar fue desarrol ada por Yu (2004) quién analizó mercado inmobiliario en Milwaukee utilizando la técnica GWR. Para ello empleó 3,437 datos seleccionados aleatoriamente del registro de propiedades maestras de 2003 de la ciudad. El modelo especificado incluyó las variables precio de la vivienda como variable dependiente y como variables independientes el área de la misma, su edad, el número de baños, el hecho de tener aire acondicionado y chimenea, el tipo de piso y las imperfecciones de la misma. Los resultados del modelo global de Yu (2004) muestran que el modelo es significativo globalmente y que las variables empleadas son estadísticamente significativas. En el caso de las regresiones geográficamente ponderadas, especifica el siguiente modelo:
Precio = f (Área, Edad, Aire acondicionado, Número de baños, Suelos imperfectos)
A partir de él obtiene varios resultados importantes: En primer lugar, con excepción del área de la vivienda las relaciones entre las características de las viviendas o del vecindario no son significativas en todas las zonas de la ciudad, contrario a lo que puede deducirse del modelo global. En segundo lugar, la cercanía de las viviendas al lago Michigan hace que los precios de las viviendas sean mucho más sensibles a sus atributos, por lo que posiblemente sea necesario incluir en el modelo una medida de distancia al lago. Por último, en algunas zonas la edad agrega valor a las viviendas, presumiblemente porque son un indicativo del valor histórico de las mismas.
Sin embargo, hasta el momento los estudios realizados con la técnica GWR en el área de precios de vivienda han sido pocos y, en términos generales, se han utilizado en la especificación de las variables intrínsecas de la vivienda como área, número de baños, edad de construcción y garajes, entre otros y adicionalmente han empleado medidas de distancia a zonas verdes, instituciones educativas, supermercados, etc. así como variables dummy con el fin de verificar la relación existente entre el medio que rodea la vivienda y su precio, obteniendo resultados significativos en la mayoría de el os. En su mayoría, las variables más empleadas en estos trabajos son las relacionadas con el área de la construcción, la edad del inmueble y medidas de distancia del inmueble a infraestructura relevante en la zona. En todos los casos, las dos primeras variables resultaron ser significativas al 99%, mientras que para el caso de la variable distancia resultó ser relevante en casos relacionados con la cercanía al mar y las escuelas, mientras que en casos como la cercanía a zonas verdes, resultaron no serlo.
Este tipo de trabajos ponen sobre la mesa la importancia de las regresiones locales desarrolladas a través de la técnica GWR, porque permiten identificar zonas en las cuales determinados parámetros del modelo no son significativos o se presentan cambios muy fuertes en las magnitudes de los mismos indicando una mayor o menor sensibilidad de las viviendas a los parámetros.
De igual manera, los estudios citados muestran las variaciones en los coeficientes de determinación obtenidos de las múltiples ecuaciones locales, exponiendo las zonas para las cuales el modelo global no representa adecuadamente la realidad del mercado.
Metodología Preliminares matemáticos y econométricos
Consideremos la especificación tradicional para el modelo lineal general en forma de ecuaciones: Yi = β1 + β2Xi2 + ... + βkXik + ui, i = 1,2, . ., N, o en notación matricial Y = Xβ + U, U  (0, σ2IN).
(0, σ2IN).
Al resolver el problema de optimización minβ U'U se tiene el estimador de mínimos cuadrados ordinarios  = (X'X)-1 X'Y. En el caso U
= (X'X)-1 X'Y. En el caso U (0, σ2Ω),Ω ≠IN se obtiene el estimador de mínimos cuadrados generalizados
(0, σ2Ω),Ω ≠IN se obtiene el estimador de mínimos cuadrados generalizados  = (X'Ω-1X)-1 X'Ω-1 Y.
= (X'Ω-1X)-1 X'Ω-1 Y.
Matriz de contigüidad especial W
Si definimos YIcomo el valor de la variable en la región i, estamos incorporando el espacio como elemento relevante en el modelo; y, teniendo en cuenta la primera ley de la geografía de Tobler (1979), que afirma ''todo tiene que ver con todo, pero las cosas cercanas están más relacionadas entre sí que las cosas lejanas'', es necesario incluir en la especificación información explicita que permita contrastar la dependencia espacial. Ord (1975) materializó este principio incluyendo en sus modelos econométricos una matriz de retardos espaciales o matriz de contigüidades W, la cual representa la materialización de la primera ley de Tobler en términos de proximidad o lejanía. La matriz resultante puede ser entonces del tipo binario, donde 1 representa la proximidad entre la región correspondiente a la fila y la columna y 0 el caso contrario (la diagonal principal estará compuesta por ceros al no tener sentido el concepto de proximidad al región consigo misma).
Al ser difícil definir de manera precisa el concepto de proximidad o lejanía entre un par de regiones, se utiliza el concepto matemático de vecindad como expresión de proximidad. Esta matriz es conocida como Matriz de Retardos Espaciales pues en su construcción se utiliza un procedimiento similar al operador de retardos utilizado en series temporales. En el contexto temporal, el operador de retardos provoca un desplazamiento en el eje del tiempo equivalente a la potencia j. Análogamente, la matriz de contigüidades W aplicada al vector Y provoca desplazamientos de masas en el espacio, obteniendo así la suma de las magnitudes de la variable en las regiones vecinas a la rezagada. WY recibe pues el nombre de retardo espacial
Especificación de algunos modelos econométricos espaciales
• Modelo autorregresivo de regresión espacial de orden 1. SAR(1)
Y = ρWY + ε, ε N (0, σ2I)
N (0, σ2I)
Esta especificación corresponde a un proceso en el cual las variaciones de la variable endógena son explicadas por las variaciones en las regiones vecinas.
• Modelo Básico de Regresión lineal
Y = Xβ + ε, ε  N (0, σ2I)
N (0, σ2I)
Esta especificación será adecuada para modelar una variable con dependencia espacial, solo en el caso en el que este efecto esté explicado en su totalidad por las variables exógenas del modelo.
• Modelo del error espacial
Y = Xβ + U
U = λWU + ε, ε N (0, σ2I)
N (0, σ2I)
Esta especificación se utiliza cuando el modelo básico de regresión lineal no es capaz de explicar el efecto espacial presente en la variable endógena, trasladando entonces este efecto hacia los términos de error.
• Modelo mixto autorregresivo de regresión espacial o modelo del retardo espacial
Y = ρWY + Xβ + ε, ε N (0, σ2I)
N (0, σ2I)
Modelos de regresión ponderados geográficamente
La especificación para el modelo de regresión tradicional
 i = 1, 2, ..., n, o en notación matricial Y = Xβ + U, U
i = 1, 2, ..., n, o en notación matricial Y = Xβ + U, U  (0, σ2IN), considera que los parámetros son invariantes en el espacio, esta especificación se puede extender para considerar el espacio de manera específica introduciendo las coordenadas del punto (ui, νi) y considerar una realización βj (ui, νi) teniendo, en cuenta estas consideraciones podemos escribir
(0, σ2IN), considera que los parámetros son invariantes en el espacio, esta especificación se puede extender para considerar el espacio de manera específica introduciendo las coordenadas del punto (ui, νi) y considerar una realización βj (ui, νi) teniendo, en cuenta estas consideraciones podemos escribir  bajo esta presentación la matriz de parámetros considera las vecindades de cada punto y está definida por:
bajo esta presentación la matriz de parámetros considera las vecindades de cada punto y está definida por:

De manera análoga a la estimación MCO, podemos estimar los parámetros de cada fila de la matriz anterior mediante

Los estadísticos utilizados en los análisis se pueden consultar en Fotheringham et al (2002).
Caso de estudio
Contexto
San Javier (ver Gráfico 1) es una comuna de estrato bajo y tamaño medio ubicada en el centro occidente de Medel ín, Colombia, la cual cuenta, según la subsecretaría de catastro municipal, con aproximadamente 29,500 predios de uso habitacional repartidos en veinte barrios, cerca del 94% corresponden a los estratos uno (ubicados en la periferia y bastante alejados de la estación del metro), dos y tres; y el 6% restante son viviendas de estrato cuatro.
Según la encuesta de calidad de vida de la ciudad, realizada en 2008, su población es de casi ciento sesenta y seis mil personas, la mayoría de los cuales son mestizas y cerca del uno por ciento son de raza negra. Aproximadamente noventa mil habitantes de la zona tienen un nivel educativo igual o inferior a educación primaria. La tasa de desempleo en el lugar es de aproximadamente el 12.5%, casi tres puntos por encima del promedio de la ciudad.
La estructura urbana de San Javier es homogénea con predominio de inmuebles residenciales unifamiliares, por encima de los multifamiliares, de los comerciales y de los de servicios, lo que ha hecho que su infraestructura vial se encuentre en regular estado y sus especificaciones luzcan inferiores frente a la cantidad de vehículos que transitan diariamente por el a. A pesar de el o, la zona cuenta con un buen sistema de transporte público integrado con el sistema metro, que permite a sus habitantes viajar rápidamente de un extremo a otro de la ciudad sin generar mayores presiones en las vías.
El sistema de transporte masivo cuenta con una estación ubicada en las inmediaciones de la carrera 99 con la cal e 45, es la última estación de la línea B, la cual comunica la zona con el centro de la ciudad. En el a confluyen todas las rutas del sistema integrado de transporte SIT que permite a los habitantes de las zonas más alejadas viajar desde sus casas en un bus hasta el sistema. La estación del metro se ha convertido en un punto de referencia en la zona debido al aumento de la calidad urbanística asociada a la construcción de la estación y reflejada en mejoras de andenes, semaforización de las vías y construcción de bahías de parqueo, entre otros, así como al continuo flujo de pasajeros que transformó la zona cercana a la estación pasando de ser netamente residencial a ser una mezcla de uso residencial con comercial.
La estación del metro de San Javier comenzó a operar junto con el resto de la línea B en 1996. A partir de entonces la zona ha sufrido cambios importantes convirtiendo en corredores comerciales zonas que antes eran residenciales gracias al importante flujo de personas que se dirigen diariamente a la estación. En la ciudad ha habido algunas discusiones importantes acerca del impacto que ha tenido el metro en la localidad, pero siempre referidos al deterioro que ha generado en el centro de la ciudad la línea A del metro que se caracteriza por estar cercana a comercio e industria, pero no a la línea B que tiene su área de influencia en zonas residenciales quizá porque su construcción se hizo sobre una canalización lo que permitió que se insertara más fácilmente en los ambientes residenciales de la zona. Cerca de la estación se encuentran ubicados un parque infantil, una escuela pública primaria, un parque biblioteca, una iglesia y la línea del metro cable, así como la calle San Juan que es un referente vial en la ciudad.
En cuanto al equipamiento urbano, la zona presenta, como en muchos otros lugares de la ciudad, déficits de espacios culturales y recreativos, sin embargo, cuenta con amplias zonas verdes en las partes altas como se observa en el gráfico 4, las cuales pueden emplearse como reservas forestales o parques ecológicos en un futuro. Como en la mayoría de las comunas de Medellín, el plan de ordenamiento territorial en San Javier permite unos mayores índices de construcción en las zonas bajas y de topografía plana y menores en las zonas altas y pendientes como una manera de regular la densificación de la ciudad. Sin embargo, los datos de las encuestas de calidad de vida de la ciudad muestran que las zonas con mayor número de viviendas por hectárea de esta comuna están ubicadas en los barrios altos como Las Independencias, La Pradera y El Pesebre, que tienen un menor nivel de desarrollo arquitectónico y urbano, mientras que algunos de los barrios con las menores densidades como San Javier No. 1 y San Javier No.2 se ubican en las zonas bajas que tienen una calidad urbanística superior, es decir, se presenta todo lo contrario a lo que busca el plan de ordenamiento territorial.
En términos del mercado inmobiliario residencial, San Javier se ha caracterizado por representar entre el cinco y el ocho por ciento del total de negocios de vivienda realizados en la ciudad y ha participado activamente en los auges y depresiones que ha sufrido el mercado inmobiliario local. Es así como durante 2002, un año regular para el mercado inmobiliario, se negociaron 1,200 viviendas, mientras que en 2006, año de auge, se transaron más de 2,200, mostrando que es una zona articulada con el desarrollo inmobiliario y comercial de la ciudad.
La motivación del estudio se centra en presentar evidencia de que el desarrollo de obras públicas en zonas menos favorecidas de la ciudad contribuye a mejorar el bienestar de sus habitantes a través de un aumento de su patrimonio expresado en términos del aumento de precio de sus viviendas. De igual forma este estudio permite clarificar el sustento económico de los cobros por valorización que realizan las administraciones locales cuando se ejecuta una intervención urbanística o se desarrolla una obra pública, los cuales usualmente generan polémica pues no es claro si valorizan o desvalorizan las propiedades, ni es clara la magnitud del impacto que generan en los precios de las viviendas.
Datos Utilizados
Para desarrol ar el estudio se emplearon datos correspondientes a 89 precios de mercado de viviendas ubicadas en los alrededores de la estación del metro en San Javier, localizados en once barrios que cuentan con 21,503 viviendas, detallados en avalúos realizados por 4 peritos distintos entre 2008 y 20091. En total la muestra representa el 0.41% del total de viviendas de los barrios estudiados, la cual es inferior a la empleada en otros de estudios de este tipo como el desarrollado por Yu (2004) que es del 0.86% en Milwaukee, pero similar a las utilizadas en Colombia dada la escasez y dificultad para conseguir los datos. Por ejemplo la muestra empleada por Medina y Morales (2006) en Bogotá es del 0.45%.
Los datos empleados fueron aportados por la Lonja de Propiedad Raíz de Medellín y Antioquia de su base de datos particular, debido a que las cifras de precios de inmuebles transados en el mercado no quedan inscritos ni en las oficinas de registro de instrumentos públicos ni en las oficinas de catastro debido a las condiciones de seguridad existentes en el país. Por tal motivo, los precios fijados en los avalúos constituyen una buena aproximación a lo que son los precios de mercado de los inmuebles y mejores que los precios de oferta que continuamente se utilizan para desarrollar este tipo de trabajos en Colombia, debido a que los precios de oferta normalmente están sobrevaluados con el fin de dejar un margen de negociación en el caso de que pueda darse un trato.
Cada dato de avalúo contiene información correspondiente a la fecha en que se realizó el avalúo, el precio de la vivienda, el tipo de inmueble avaluado (casa o apartamento), la edad de la construcción, el área construida, el área del parqueadero si lo tiene, el número de baños, el nombre del edificio o la unidad residencial en que está ubicada la vivienda si es el caso y una serie de características de la unidad residencial o del edificio como son tener ascensor, portería, tanque de agua, parqueadero de visitantes, juegos de niños, piscina, sauna, turco, entre otros.
En el Gráfico 2 se observa el plano de la zona, en donde cada punto representa un dato de avalúo. También se marca la localización de la estación del metro, la vía de acceso del tren y las curvas de nivel que indican la topografía del terreno con mayor pendiente en la zona inferior izquierda del gráfico y un terreno más plano hacia la derecha y parte superior del gráfico.
Las estadísticas descriptivas en la Tabla 1 muestran la diversidad de las viviendas de la zona, que incluyen viviendas con edades de construcción que van desde uno hasta los sesenta años, áreas entre los veintiséis hasta los doscientos treinta y ocho metros cuadrados, con distancias a la estación del metro que oscilan entre los 0.09 y los 1.8 kilómetros, con estratos que varían entre dos y cuatro:
En las franjas cercanas a la estación del metro existen casas antiguas con grandes áreas y precios elevados mezcladas con apartamentos de pequeñas áreas y precios altos, mientras en los lugares más alejados y ubicados mucho más al occidente hay apartamentos y casas con menores áreas construidas, de estrato más bajo, algunas de ellas ubicadas en unidades cerradas con algunas características importantes como parqueaderos de visitantes, juegos de niños y portería. Mientras que las viviendas ubicadas un poco más al oriente tienen una mezcla de casas antiguas de áreas grandes, con apartamentos relativamente nuevos, de áreas pequeñas y altos precios.
Las variables empleadas para desarrollar el estudio y los signos esperados de las mismas se detal an en la Tabla 2.
Resultados
En la siguiente sección se presentan los resultados obtenidos utilizando mínimos cuadrados ordinarios, regresiones espaciales y regresiones ponderadas geográficamente, a partir de los cuales se realizan comparaciones y se obtienen las conclusiones.
Estimación por mínimos cuadrados ordinarios
Log (Precio) = f (fecha, Inmueble, Edad, Edad2, Construcción, Parqueadero, Distancia, Estrato2, Estrato3, Baños, Unidad, Características, error) es la especificación estimada por mínimos cuadrados ordinarios y cuyos residuales resultaron ruido blanco, los resultados aparecen en la Tabla 3.
En primer lugar, el modelo ajustado explica cerca del 83% de la variación en los precios de las viviendas. En segundo lugar el modelo presenta los signos esperados para todas las variables y podemos ver que si se incrementa en un metro cuadrado el área construida de la vivienda, en promedio, el precio total de la vivienda aumenta en un 0.60%. De igual forma, el modelo permite corroborar la hipótesis de la influencia de la estación del metro en los valores de las viviendas: un incremento de un kilómetro en la distancia a la estación del metro, manteniendo todo lo demás constante, genera, en promedio, una reducción de un 20% en el precio total de la vivienda.
Uno de los aspectos centrales con datos georreferenciados es la posible presencia de autocorrelación y de heterogeneidad espacial, que no son considerados en la modelación por mínimos cuadrados ordinarios y que por tanto se hace indispensable introducir a través de modelos de regresión espacial. En este caso para ampliar el análisis se estimarán en las secciones siguientes un modelo autorregresivo espacial de orden uno SAR(1) y un modelo de error espacial
Modelos espaciales
La naturaleza de la información utilizada hace necesario un contraste de autocorrelación espacial; los datos utilizados muestran que el p-valor del estadístico I de Moran es de 0.0010 y por tanto no se tiene evidencia a favor de hipótesis nula de no autocorrelación espacial con un nivel de confianza del 95% (ver el scatterplot de Moran en el Gráfico 3); esto hace que sea necesario tener en cuenta explícitamente los efectos espaciales utilizando una matriz de contigüidad espacial W en la estimación. La matriz de pesos espaciales W, fue generada con el método k-NearestNeighborhood igual a 4, que es el número de viviendas que se asume tienen características similares en la zona, relacionadas con edades, tipos y características
Utilizando el programa Geoda se estimaron tipos de modelos espaciales uno con rezago espacial y otro con error espacial. La especificación para el modelo con rezago espacial fue la siguiente:
Precio=f(W*Precio,fecha,Inmueble,Edad,Edad2,Construcción,Parqueadero, Distancia, Estrato2, Estrato3, Baños, Unidad, Características, error).
Los resultados de la estimación presentados en la Tabla 4 muestran un mejor ajuste con respecto a la del modelo OLS. Las variables fecha, construcción, parqueadero, distancia, estrato2, estrato3 y baños son significativas al 99%, mientras que la variable características lo es al 90%.
Luego, se estimó un modelo con error espacial en el cual no se presentaron problemas de autocorrelación espacial ni de heterocedasticidad cuya forma funcional es:
Precio = f (fecha, Inmueble, Edad, Edad2, Construcción, Parqueadero, Distancia, Estrato2, Estrato3, Baños, Unidad, Características, error) Error = W*error + μ
Los resultados del modelo con error espacial, muestran que las variables construcción, parqueadero, distancia, estrato2, estrato3, baños y el coeficiente Lambda que contiene el retardo espacial son significativos al 99%, mientras que las variables fecha y edad lo son al 95%. La variable edad2 lo es al 90%.
Modelo GWR
A través del programa GWR se estimó una regresión ponderada geográficamente. El ancho de banda empleando un kernel adaptativo, y el criterio de minimización de Akaike luego de ocho iteraciones aparecen la Tabla 6:
El modelo GWR presentó el coeficiente de determinación mayor, entre todos los modelos estimados, explica el 92.3% de la variación en los precios de las viviendas
Criterio de información de Akaike 3,231.515
Coeficiente de Determinación 0.923
r2 Ajustado 0.8762
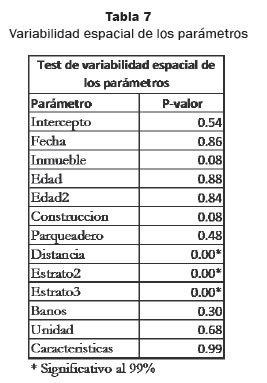
El examen de la variabilidad espacial de los parámetros locales se realiza a través de un test de Monte Carlo (Tabla 7). Los resultados muestran que los parámetros Distancia, Estrato2 y Estrato3 presentan una variabilidad espacial significativa, lo que implica que hay una alta probabilidad de que no haya ocurrido aleatoriamente, mientras que los parámetros restantes presentan un nivel de variabilidad espacial con alta probabilidad de ser obtenida al azar.
El Gráfico 4 muestra en la columna izquierda planos de cómo varían los niveles de los coeficientes de las características cuya variabilidad espacial resultó significativa (Distancia, Estrato2 y Estrato3). En la columna derecha los planos muestran como varía la significancia de los parámetros de las ecuaciones2. Los resultados del estudio muestran que el coeficiente de la variable Distancia es significativo en toda la zona que circunda la estación del metro (gráfico 4b). Los coeficientes asociados a esta variable (gráfico 4a), presentan grandes valores en las zonas aledañas a la estación del metro, mostrando una fuerte influencia positiva de esta estación en los precios de las viviendas en un radio de aproximadamente 600 metros. Este efecto se explica porque la zona de influencia se beneficia de las mejoras urbanísticas desarrolladas en el entorno de la estación, como perfeccionamientos de andenes, bahías para vehículos y ubicación de semáforos. Sin embargo, la influencia de la estación del metro en los precios de las viviendas se reduce en la medida en que se presentan depresiones naturales del terreno, como ocurre en la parte central derecha del plano, y en la medida en que la división de las manzanas es menos regular y las vías más estrechas.
Las variables Estrato2 y Estrato3 indican pertenencia de las viviendas a los estratos 2 y 3. El estrato de una vivienda es determinado por las oficinas de catastro en función de características externas de la vivienda: estado de los andenes, vías de acceso y cercanía a focos de contaminación; así como de características propias de la vivienda: materiales de construcción de fachadas y techos, entre otros. En la parte izquierda de los gráficos 4c y 4e, los coeficientes de las variables muestran una gran influencia en los precios de las viviendas de la zona con coeficientes negativos pues los andenes, las vías, la topografía y los materiales de construcción de las viviendas son de menores especificaciones que las del resto de la zona y este tipo de características exógenas en mal estado como andenes, vías de acceso, etc. tienden a reducir el precio de una vivienda. Es importante destacar que aunque la existencia de la estación muestra una influencia positiva en los precios de la vivienda, el gráfico 4c muestra como las viviendas cercanas a las vías de acceso del metro a la estación muestran decrementos significativos en sus precios.
En cuanto al poder explicativo de las ecuaciones, todas las regresiones locales presentan valores entre 86.7% y 91.9%, como consecuencia de la utilización de un kernel adaptativo y de un modelo con variables explicativas adecuadas similares a las empleadas en otros estudios.
Con el fin de analizar las diferencias entre la estimación GWR y el método de mínimos cuadrados ordinarios se estimaron los precios de una vivienda tipo localizada en diferentes sectores del área de estudio. Las características de la casa tipo son: 72.69 m2 construidos, edificada hace 14 años, estrato socioeconómico 3, ubicada en unidad cerrada, con tres baños y un parqueadero de 11.5 m2. En el Gráfico 4 se muestra las localizaciones dadas a la casa tipo y se indican los precios obtenidos con GWR y OLS. La Tabla 8 indica la distancia de la vivienda a la estación del metro y los precios obtenidos con cada metodología.
Los resultados muestran que los valores de la vivienda obtenidos a través de GWR tienden a variar más dramáticamente en el espacio de lo que lo hacen los valores obtenidos por OLS; esto se debe a que con GWR los parámetros cambian continuamente en el espacio, ajustándose a características como el estrato y la edad; mientras que la técnica OLS sólo arroja resultados promedio de las variables. Un ejemplo claro se puede observar en la diferencia de precios que se obtienen al localizar la vivienda tipo a 0.90 y 0.91 kilómetros de la estación (prácticamente equidistantes), pero en sentidos opuestos. Esta diferencia en so localización produce una diferencia de precios de $44,940,588 ($109,535,527-$64,594,939) según GWR, y de $205,478 (70,654,029 - $70,850,507) según OLS. En ambos casos los precios obtenidos por GWR se acercan más a los precios reales de las viviendas circundantes. Esto implica que la tendencia de la metodología OLS a producir valores promedio de los parámetros puede llevar a subvalorar o sobrevalorar significativamente el precio de una vivienda.
Conclusiones
En este trabajo se estudian diferentes modelos para determinar la influencia de la estación del metro de San Javier en los precios de las viviendas de la zona. El modelo de GWR se posiciona como el más apropiado para tal objetivo gracias a su capacidad de permitir que los coeficientes del modelo hedónico varíen en magnitud y nivel de significancia dependiendo de la localización de la vivienda que se esté valorando.
La variable correspondiente a la distancia entre la vivienda y la estación del metro de San Javier resultó ser significativa, y muestra una influencia positiva de la estación del metro en los precios de las viviendas localizadas en un radio de 600 metros. Sin embargo, se detecta una influencia negativa en los precios de las viviendas que se localizan en los costados de las vías de acceso del metro a la estación.
La posibilidad que ofrece GWR de delimitar espacialmente la zona de influencia de una nueva infraestructura en los precios de las viviendas puede ser de utilidad para la determinación del área geográfica que podría ser sujeto de impuesto de valorización.
Futuras investigaciones en esta área se enfocarán en la exploración de nuevas formas funcionales para la determinación de kernels y en procedimientos que utilicen splines.
Notas al pie
1 La utilización de precios de mercado, a diferencia de los precios de catastro, asegura la utilización de precios más precisos y confiables.
2 Los mapas de los coeficientes de las demás variables pueden ser suministradas por los autores de este artículo.
Referencias
Agudelo, G. (2010). Dependencia Espacial: Detección, Validación y Modelación. TesisMaestría en Matemáticas Aplicadas. EAFIT. [ Links ]
Anselin, L. (1988). Spatial Econometrics: Methods and Models. Dordrech: Kluwer. [ Links ]
Anselin, L. (2003). Spatial externalities, spatial multipliers, and spatial econometrics. International Regional Science, 26, 153–166. [ Links ]
Basu, S., Thibodeau, TG.(1998). Analysis of spatial autocorrelation in house prices. Journal of Real Estate Finance and Economics, 17, 61-85. [ Links ]
Beaty, J. (1952). Rental real estate often a good investment. Med Econ, 5(6), 93–94. [ Links ]
Bitter, C., Mulligan, G., & Dall'erba, S. (2007). Incorporating spatial variation in housing attribute prices: a comparison of geographical y weighted regression and the spatial expansion method.Journal of Geographical Systems, 9(1), 7-27. [ Links ]
Brunsdon, C., Fotheringham, S., Charlton, M. (1998). Geographical y weighted regression – modeling spatial non-stationarity. The Statistician,47(3), 431-443. [ Links ]
Can, A. (1992). Specification and estimation of hedonic house Price models. Regional Sciences and Urban Economics, 22, 453-474. [ Links ]
Carroll, T., Clauretie, T., Jensen, J. (1996). Living next to godliness: Residential property values and churches. Journal of real estate finance and economics. 12(3): 319 – 330. [ Links ]
Cho, S., Bowker, J., Park, W. (2006). Measuring the Contribution of Water and Green Space Amenities to Housing Values: An Application and Comparison of Spatial y Weighted Hedonic Models.Journal of Agricultural and Resource Economics, 31(03), 485 – 507. [ Links ]
Dewey, L., DeTuro, P. (1950). Should I invest in real estate? Med Econ, 28 (3), 85–93. [ Links ]
Dubin, R., Goodman, A. (1982). Valuation of education and crime neighborhood characteristics through hedonic housing prices.Population and environment, 5(3), 166–181. [ Links ]
Fotheringham, A., Brunsdon, C., and Charlton, M. (2002). Geographical y Weighted Regression: The Analysis of Spatial y Varying Relationship. John Wiley and Sons, Ltd., West Sussex, UK. [ Links ]
Frech, H., Lafferty, R. (1984). The effect of the California coastal commission on housing prices.Journal of Urban Economics, 16(1), 105–123. [ Links ]
Grudnitski, G., Do, Q. (1997). Adjusting the value of houses located on a golf course. The appraisal Journal,65(3), 261-266. [ Links ]
Lancaster, K. (1966). A new approach to consumer theory.Journal of Political Economy, 74(1), 132–157. [ Links ]
LeSage, JP. (2004). A family of geographical y weighted regression models.Advances in spatial econometrics. Methodology, tools and applications, 241-264. [ Links ]
LeSage J., Peace, K. (2004). Spatial statistics and real estate.Journal of Real Estate Finance Economics, 29, 147–148. [ Links ]
LeSage, J., Peace, K (2009). Introduction to Spatial Econometrics.CRC press. [ Links ]
Medina, Carlos; Morales, Leonardo y JairoNuñez.(2010). Quality of life in urban neighbourhoods of Bogotá and Medellín. The Quality Life in Latin American Cities: Markets and Perceptio. Editado por Eduardo Lora, Andrew Powel , Bernard M.S. van Praag y Pablo Sanguinetti, BID y BM. [ Links ]
Mei, C., He, S., Fang, T. (2004). A note on the mixed geographical y weighted regression model. Journal of Regional Science, 44(1), 143-157. [ Links ]
Mennis, J. (2006). Mapping the results of geographical y weighted regression. Cartographic Journal, 43(2), 171-179. [ Links ]
Pace, R., Kelley, R., Sirmans, C. (1998). Spatial Statistics and Real Estate. Journal of Real Estate Finance and Economics, 17, 5–13. [ Links ]
Pavlyuk, D. (2009). Statistical analysis of the relationship between public transport accesibility and flat prices in Riga. Transport and telecomunication,10(02), 26–32. [ Links ]
Portney, P. (1981). Housing prices, health efects, and valuing reductions in risk of death. Journal of environmental economics and management, 8(1), 72–8. [ Links ]
Rosen, S. (1974). Hedonic prices and implicit markets: product differentiation and pure competition. Journal of Political Economy, 82, 34–55. [ Links ]
Yu, D. (2004). Modeling housing market dynamics in the city of Milwaukee: a geographical y weighted regression aproach. Recuperado de: http://www.ucgis.org/ucgisfal2004/studentpapers/files/danlinyu.pdf [ Links ]