INTRODUCCIÓN
El constante incremento del consumo de energía eléctrica (CEE) [1-2], estrechamente ligado al desarrollo socioeconómico [3-4], se ha convertido en uno de los temas que más ocupa la atención de políticos y científicos, tanto para determinar políticas de energía [3-5] como para considerar la disminución de costos en todos los puntos de su proceso de producción (generación, distribución y consumo, con énfasis en este último) [6-7] y preservar el medio ambiente [8-9]. La marcada tendencia a la desregulación del mercado de la energía eléctrica [10-11], los cambios climáticos [12-13], la expansión del uso de las energías renovables [14] y la escasez de combustibles fósiles hacen más complejo el escenario; por lo tanto, contar con pronósticos de CEE que den cuenta acabadamente de esta complejidad se vuelve un desafío.
Las investigaciones en pronóstico de CEE abarcan un conjunto variado de diferentes aristas del problema, por esta razón se encuentran, tanto trabajos referidos a pronósticos de consumo a largo plazo [1-5], que parten de considerar la correspondencia entre factores socioeconómicos y valores de consumo, como de mediano [4-8] y corto plazo [15-16] donde se consideran otras variables como la temperatura y el día de la semana. Resulta recurrente en la mayoría de los estudios revisados, la dificultad que reviste la selección de variables de entrada [10-17], ya sea por determinar cuáles considerar/no considerar o por la cantidad de datos históricos que habría que incluir, haciendo más compleja aún la definición del modelo de pronóstico.
De forma general, en los estudios sobre pronóstico de CEE y de acuerdo con las restricciones identificadas, se seleccionan los modelos más adecuados o se considera la definición de un nuevo modelo. El objetivo en la mayoría de los casos es encontrar aquel modelo del que se obtengan los pronósticos más precisos, al tiempo que pueda atender la variabilidad de las condiciones en las que tiene lugar el consumo [11-17], por ejemplo, adaptarse a los cambios en los patrones de comportamiento de los consumidores, temperatura ambiental, luminosidad, etc. Para ello, en varios estudios se realizan análisis comparativos entre modelos preexistentes y el modelo propuesto a través de técnicas de medición de error, determinándose el porcentaje de mejora que aportan y en qué aspectos de su desempeño resultan particularmente superiores (por ejemplo, costos computacionales y tiempos de entrenamiento) [16].
Como alternativas, y en aras de una mejor solución, varios autores proponen modelos híbridos que resultan de la combinación de otros ya existentes [1-10], logrando así conjugar las ventajas de los métodos implicados y disminuir las desventajas.
Todos estos estudios proporcionan información relevante de los modelos de predicción de CEE en diferentes escalas de tiempo y haciendo uso de diversas técnicas.
De esta forma, para poder compararlos es necesario clasificarlos bajo algún patrón común que los agrupe. Adicionalmente, se deben describir detalladamente cada uno de los elementos que los componen, así se posibilita la identificación de oportunidades de investigación en el área de pronóstico de CEE. En este sentido, este trabajo propone una revisión sistemática de literatura (RSL) para conocer el estado del arte sobre las técnicas o modelos utilizados para pronosticar CEE, sus características y métodos de evaluación de precisión. El resto del artículo se organiza de la siguiente forma: en la sección 1 se muestra la metodología utilizada para llevar a cabo la RSL. Se describen cuáles fueron los criterios de selección de los artículos considerados, los contenidos de los artículos revisados. Las características de los modelos propuestos en cada uno de los artículos contemplados en la revisión son presentadas a través de gráficos y tablas estadísticas en la sección 2. La sección 3 ofrece un análisis comparativo de los mismos a fin de visualizar sus avances y limitaciones. Finalmente, la sección 4 resume y expone las conclusiones del artículo y se plantea una nueva línea de investigación.
1. METODOLOGÍA
La metodología que se siguió para la RSL fue originalmente desarrollada para el ámbito de investigación médica y luego ampliada al campo de estudios de gestión y administración [18]. La misma está compuesta por tres etapas: i) planeación de la revisión, ii) desarrollo de la revisión y iii) desarrollo de reportes y diseminación. Para la primera etapa se tienen las siguientes fases: identificación de la necesidad de una RSL, preparación de una propuesta para la revisión y desarrollo de un protocolo de RSL. En la segunda etapa se consideran la identificación de la investigación, selección de los estudios, evaluación de la calidad del estudio, extracción de los datos, monitoreo del progreso y síntesis de la información. Finalmente, en la última se contemplan el reporte, las recomendaciones y el paso de la evidencia a la práctica.
El objetivo de esta metodología es localizar los estudios relevantes relacionados con las preguntas de la investigación a desarrollar, así como evaluar y sintetizar sus respectivas contribuciones e informar de manera clara los resultados y las conclusiones obtenidas a partir de ellos, con el in de plantear sus campos de aplicación y nuevas investigaciones [19].
Asimismo, esta metodología se adoptó en aras de reducir el riesgo de sesgado en la selección de la bibliografía por preferencias subjetivas, adoptando para ello estrategias de búsqueda, cadenas de búsquedas predefinidas, criterios de exclusión/inclusión y, al mismo tiempo, ampliar el espectro de la búsqueda más allá del horizonte de la propia experiencia.
1.1 PLANEACIÓN DE LA REVISIÓN
Las principales investigaciones en esta área son impulsadas por la utilización de distintas técnicas y modelos, la selección de variables de entrada y la cantidad de historia a utilizar, así como por técnicas para medir la precisión de los resultados. Por tal motivo, es necesario comprender todos los aspectos que involucra desarrollar un modelo de pronósticos de CEE, con el fin de entender las evidencias y desafíos actuales en el pronóstico del consumo de energía. Para ello, se pretende responder las siguientes preguntas de investigación:
PI1: ¿Qué técnicas/modelos se utilizan para la predicción/pronóstico de consumo de energía?
PI2: ¿Qué variables de entrada usan estas técnicas/modelos?
PI3: ¿Qué técnicas se utilizan para evaluar la precisión de las técnicas/modelos? ¿Cuál es la más usada?
1.2 Desarrollo de la revisión
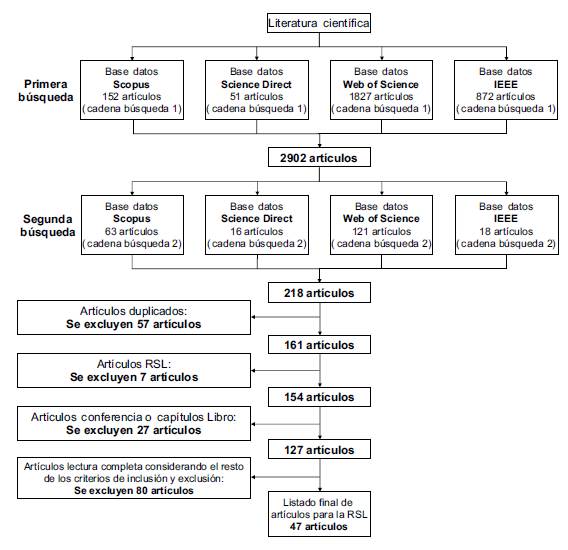
El primer paso de la RSL fue definir las cadenas de búsqueda usando palabras clave que estuvieran relacionadas con la definición del problema de investigación, con la intención de garantizar los resultados buscados. Para esto se utilizó la combinación de las palabras Energy, Consumption y Forecasting formando la frase Energy Consumption Forecasting. A continuación, se determinaron las bases de datos científicas de donde se obtuvieron los artículos a partir de dicha cadena de búsqueda. Inicialmente se buscó con ella con un ámbito que comprendió el título (title), el resumen (abstract) y las palabras claves (keywords) pero debido al gran número de artículos que se obtuvieron, alrededor de 2.900, se decidió restringir el ámbito de búsqueda de la cadena formada solo al título de los artículos. La tabla 1 muestra las cadenas de búsqueda utilizadas según la sintaxis propia de cada base de datos.
En total se obtuvieron 218 artículos combinando los resultados de las bases de datos. A partir de estos resultados se realizó el proceso de selección de los artículos evidenciado y descrito en la figura 1. Además, para la eliminación de los artículos se tuvieron en cuenta los criterios de selección definidos en la tabla 2.
Como resultado final del proceso de selección se obtuvieron 47 artículos listados en la tabla 3, ordenados de acuerdo con el ranking de citación.
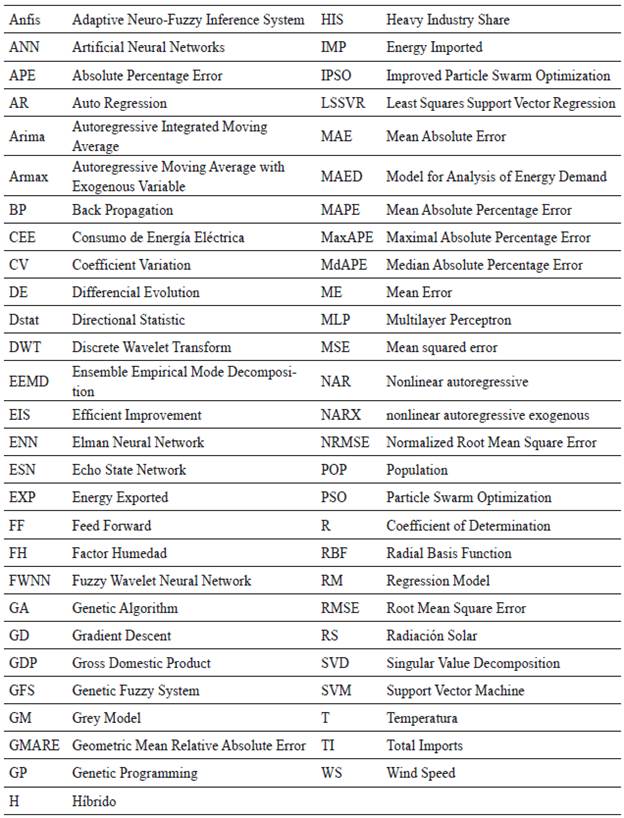
Los acrónimos utilizados en esta RSL (tabla 4):
1.3 Reporte y diseminación
Como parte de esta etapa, se realizó una agrupación de los artículos seleccionados por tipo de método/modelo de pronóstico y luego, de acuerdo con el alcance establecido para el pronóstico, en corto y largo plazo. Dentro de cada uno de los grupos, se resumen las características y ventajas más relevantes de los modelos propuestos.
1.4 Artificial neural network (AN N)
1.4.1 Corto plazo
En 2004 Bacznski y Parol [39] entrenaron varios modelos de ANN de tipo MLP y concluyeron que el número de peso en la red neuronal debería ser de un orden de magnitud menor que el número de datos de aprendizaje. También observaron que la proporción de número de neuronas en las capas ocultas tiene una influencia considerable en la habilidad de la red neuronal para aprender y generalizar, siendo las mejores las de estructuras balanceadas. Los resultados obtenidos muestran que la estructura ANN tiene una influencia esencial en la calidad de los pronósticos de consumo de energía eléctrica.
Posteriormente, en 2016 Rojas-Rentería et al. [55] investigaron un sistema de pronóstico y monitoreo basado en una red neuronal de tipo MLP aplicada en un edificio real. Propusieron un modelo con tres capas. En la capa de entrada utilizaron tres entradas (CEE, hora y día) y en la de salida el CEE con granularidad horaria. Evaluaron el modelo propuesto con distintas configuraciones encontrando que el mejor resulto lo ofrecía la configuración 3-1-1 con un nivel de confidencia del 95 % en la predicción.
En 2008 Hernández y Sanzovo [20] compararon su modelo propuesto de ANN de tipo FF con un software de simulación que pronostica la demanda de energía para la administración del edificio de la Universidad de Sao Paulo. El modelo fue entrenado con tres datasets organizados de diferentes formas: una para todos los días de la semana sin discriminar días laborables de fines de semana, otra para los días laborables y la tercera solo para los fines de semana. La primera presentó mayor error entre la predicción y los datos reales en comparación con las otras dos independientemente de la cantidad de capas ocultas y números de neuronas en cada capa oculta. Entonces incrementaron la complejidad del modelo agregando como variables de entrada la temperatura exterior, la humedad relativa, la radiación solar global y la radiación solar difusa. Concluyeron que se acercaron más a los datos reales cuando discriminaron los datasets por fines de semana y días laborables, aunque la inclusión de parámetros climáticos adicionales mejoró levemente los resultados. Finalmente, los resultados mostraron que el modelo de ANN de tipo FF no es el más adecuado para la predicción en este contexto de estudio.
M. Alobaidiam etal. [58] en el 2018 presentaron un marco de referencia (framework) para predecir el promedio de consumo diario de energía de casas individuales, a partir del uso de un modelo ensamblado que emplea diversidad de información. La propuesta se aplicó en un caso de estudio en Francia. Este modelo supera la generalización de la habilidad y atenuación de varios problemas de predicción inestables de otros modelos, al tiempo que mejora el desempeño de predicción con datos limitados. Construyeron un framework con siete submodelos, uno para cada día de la semana, con parámetros determinados a través de estudios de validación cruzada. La validación Jackknife fue usada para determinar los valores óptimos de me y mc del modelo propuesto de cada configuración de ensamble. El proceso fue repetido hasta obtener las estimaciones de ensambles para todas las observaciones disponibles. En la comparación con una red neuronal normal y otra de tipo Bagging quedó demostrado que su desempeño era superior.
Ante la situación planteada por Wang et al. [16] en 2016, donde los pronósticos en la industria de facturación de equipos requieren un constante entrenamiento debido a que nueva información se genera en forma continua, propusieron una solución utilizando Hadoop. Contrastaron tres modelos: el MR-OSELM-WA, el Functional Networks y SVM. Los resultados obtenidos les permitieron demostrar que el mejor modelo era MR-OSELM-WA, el cual evidenció que las tecnologías de procesamiento BigData son efectivas para resolver este tipo de problemas dado que acortan los tiempos de entrenamiento, reducen los recursos computacionales y mejoran la precisión del pronóstico.
En el escrito presentado en 2016 por Stareverov y Gnatyuk [17], para resolver los problemas de pronóstico independientemente de la naturaleza de los datos ingresados, plantearon construir un conjunto de ANN con el fin de crear un sistema de pronóstico de carácter universal, capaz de promediar las salidas de las distintas redes neuronales individuales. Los estudios permitieron determinar el conjunto mínimo de factores relevantes, la profundidad y dimensión del vector de entrenamiento de entrada. Finalmente comprobaron que una estructura de tres niveles de conjuntos de redes neuronales tiene un poder predictivo de alto dominio y su uso resulta ser prometedor para tareas relacionadas con información y análisis estadístico.
El estudio de Ruiz et al. [49] del 2018, derivó de investigaciones previas donde se utilizaron modelos de pronóstico NAR y NARX. Además, propusieron usar un modelo de red neuronal denominado ENN entrenado con un GA. Puede señalarse que GA resultó ser un factor clave para optimizar las ANN y mejorar los modelos NAR y NARX, mientras que el modelo ENN aportaba mayor exactitud, pero resultaba más complejo por el incremento de componentes de la red neuronal que involucraba. Finalmente, la combinación de ENN + GA, considerando como variables de entrada el consumo de energía eléctrica y la temperatura, resultó ser el mejor modelo.
1.4.2 Largo plazo
En el estudio presentado en 2007 por Hamzacebi [24], este propuso un modelo ANN de tipo MLP basado en valores de observación de un año. Realizó pronósticos de consumo de electricidad en los sectores básicos hasta 2020 comparándolos con los realizados por el MAED utilizado por el gobierno y demostró que eran más exactos. Sin embargo, el objetivo del estudio no pretendía reclamar la constante superioridad del modelo ANN sino indicar a los funcionarios políticos la importancia del uso alternativo de formas de pronóstico.
En el 2008 Azadeh et al. [22], presentaron un modelo ANN de tipo MLP para el consumo anual de electricidad en sectores industriales de alto consumo de energía, si bien tradicionalmente las ANN habían sido utilizadas en pronósticos de corto plazo. Probaron varios modelos de ANN variando el número de neuronas en las dos capas ocultas y el método de entrenamiento, concluyendo que a partir de datos reales de consumo en Irán en el período 1979-2003, el modelo con la configuración 5-3-2-1 era el que pronosticaba con mejor precisión.
Ese mismo año, los mismos autores [27] presentaron otro estudio en el que proponían un algoritmo integrado para el pronóstico mensual de consumos de energía eléctrica basado en ANN, una simulación de computadora y el diseño de experimentos usando procedimientos estocásticos. Para ello, construyeron tres modelos: algoritmo integrado basado en ANN, ANN de tipo times series y ANN simulado. Buscando demostrar la aplicabilidad y superioridad de estos usaron datos reales de consumo de energía de Irán por 130 meses. Aplicaron la red MLP con tres variables de input y pudieron demostrar que la ANN de tipo MLP con configuración 3-2-1 y algoritmo de BP tuvo el mejor resultado con un error relativo igual a 0,012. Además, el modelo ANN era superior con relación al modelo ANN de tipo Time Series y el modelo simulado. Sin embargo, argumentaron que el uso de los tres modelos asegura el mejor resultado para datos reales minimizando el sesgo de utilizar un solo enfoque.
En el estudio de Jiang et al. [46] de 2013, presentaron un modelo de pronóstico de consumo de energía eléctrica basado en ANN de tipo FF entrenado por PSO. El modelo utilizaba como datos de entrada los consumos eléctricos de energía del equipo, los parámetros del equipo y los parámetros de mantenimiento del equipo. Resultados experimentales les permitieron demostrar la capacidad del modelo para mejorar la precisión de los pronósticos y avanzar en el entendimiento de la relación entre el consumo de energía eléctrica y las variables de entrada.
Mishra y Singh [59] presentaron en 2015 un modelo de red neuronal de tipo FF, que tiene el algoritmo Windowed Momentum. La inclusión de este componente permitió a los operadores superar los problemas por sobrepasar la mínima en iteraciones pequeñas que suelen tener lugar en este tipo de propagación. Igualmente, observaron que si bien, días diferentes de la semana presentaban consumos diferentes de energía, las curvas de consumo para los mismos días dentro del mes en cada año eran casi iguales. Concluyeron que el uso del algoritmo Windowed Momentum resultaba ser más eficiente que el Standard Momentum.
Nasr et al. [34] en 2002, construyeron cuatro modelos de ANN de tipo BP para pronosticar el consumo de energía eléctrica: uno de tipo univariado con tres parámetros de entrada de EEC y otros tres de tipo multivariado con distintas variables de entrada, el primero de estos combinaba las variables EEC y la T, el segundo, empleaba TI y EEC, y el tercero EEC, TI y la T. Los modelos fueron entrenados, probados y evaluados con información real del Líbano entre los periodos 1995-1999. Los resultados mostraron que los modelos multivariados resultaron superiores y dentro de ellos, el que usaba la temperatura y EEC logró el mejor desempeño en el pronóstico.
En 2006 Sözen et al. [33], pronosticaron el consumo anual de energía eléctrica de Turquía usando una técnica de red neuronal de tipo BP. Los resultados experimentales les permitieron demostrar que el modelo propuesto lograba predecir dentro de los errores aceptables, utilizando como variables de entrada el año, la población del país, la capacidad instalada de generación y la generación bruta total del país.
En el estudio presentado en 2017 Zeng et al. [5], plantearon mejorar el modelo de pronóstico basado en ANN de tipo BP incluyendo el algoritmo inteligente llamado DE. Este modelo fue comparado con otros modelos planteando dos escenarios, el primero utilizaba las variables GDP, POP, IMP y EXP y el segundo, solo la variable CEE. Finalmente confirmaron que el modelo propuesto era el más preciso y de fácil implementación.
Meng et al. en 2014 [4] presentaron un modelo Hybrid Grow, que incluía un término constante, uno lineal y otro exponencial, combinado con un algoritmo Multiwindow Moving Average, que descompone los consumos mensuales en varias series periódicas. Este modelo fue contrastado con otros como Arima y ANN, y concluyeron que el modelo propuesto daba mejores resultados para el pronóstico de consumos de energía anual de China.
En 2018 Wang et al. [56], propusieron un nuevo modelo de ANN de tipo ESN que usaba el algoritmo DE, para determinar sus parámetros de configuración, con el fin de pronosticar consumos mensuales y anuales de energía eléctrica para una ciudad de China. Este modelo resultó tener características de fácil implementación y estabilidad, así como superioridad sobre otros modelos en cuanto a la precisión del pronóstico tales como el Arima, BBPN, basic ESN y ESN-GA.
1.5 Autoregressive IntegratedMovingAverage (Arima)
1.5.1 Corto plazo
Kamaev et al. [44] en 2012, propusieron un modelo Arima con cuatro lags de entrada de consumos de energía. Construyeron además dos modelos de regresión lineal: uno con cuatro lags de consumos de energía eléctrica de entrada al modelo y otro con más entradas adicionales como la temperatura y los parámetros del edificio. Posteriormente implementaron otro modelo de ANN el cual tenía como parámetros de entrada los cuatro lags de consumo de energía eléctrica, la temperatura y los parámetros del edificio. Como resultados finales obtuvieron que el modelo Arima era el de ejecución más rápida, pero con menor precisión en el pronóstico de acuerdo con la métrica de error MAPE y el modelo de ANN el de mejor pronóstico.
En 2013 Yoo y Hur [47], emplearon un modelo denominado Armax usando el filtro Kalman para estimar los parámetros del modelo pronosticando los consumos de energía eléctrica, con una granularidad horaria en función de su historia y la variable exógena de temperatura. Además, la serie de tiempo fue dividida en dos series, una con los días entre semana y la otra con los días del fin de semana. Finalmente, las simulaciones efectuadas demostraron la efectividad del modelo propuesto.
Zhang et al. [52] en 2017, presentaron un marco de referencia (Framework) con el objetivo de mejorar el pronóstico de consumos eléctricos fotovoltaicos (PV) para plazos de tiempos muy cortos, usando el comportamiento histórico del consumo de electricidad y la información climática como la temperatura, la solar global horizontal irradiance, la humedad relativa, la velocidad del viento y las precipitaciones. La propuesta incluía varios modelos de pronóstico, entre ellos un modelo Arima, un modelo de SVM y varios modelos ANN. Como conclusión dejaron abierta la posibilidad de una investigación futura orientada a incorporar en el Framework la selección automática del modelo atenta a establecer el óptimo para cada contexto específico.
1.5.2 Largo plazo
En 2001 Saab et al. [26], estudiaron diferentes técnicas de modelado univariado para pronosticar los consumos mensuales de energía eléctrica del Líbano usando modelos Arima. Definieron tres modelos: el Arima simple, el AR (1) simple y una configuración nueva combinando el modelo AR (1) con un highpass, siendo este último el que obtuvo mejores resultados con respecto a los otros.
En el artículo publicado por Tang et al. en 2014 [8], con el fin de mejorar la precisión del pronóstico del consumo de energía nuclear, se presentó una metodología para formular un modelo Arima de pronóstico basado en las características propias de los datos de muestra. Para esto, los autores construyeron dos modelos adicionales ANN y SVM, con el fin de validar el modelo formulado. Demostraron que el método propuesto mejoraba los desempeños de pronóstico en comparación con los otros que ignoran las características de los datos.
En 2016 Sen et al. [42], desarrollaron y evaluaron modelos de pronóstico de consumo de energía mensuales en el sector industrial de producción de hierro y acero de India. Probaron varias configuraciones de modelos Arima y finalmente determinaron que el modelo Arima (1,0,0) x (0,1,1) era el de mejores resultados para la predicción de CEE.
Meira de Oliveira y Cyrino Oliveira [57] en 2018, propusieron evaluar varios modelos para pronosticar el consumo mensual de energía eléctrica utilizando Bagging, Arima y un suavizado exponencial como Holt-Winters. La serie de tiempo de consumos de energía eléctrica fue descompuesta en componentes más simples utilizando la técnica Seasonal-Trend Decomposition using Loess (STL Decomposition), la cual permitió obtener las series de tendencia, la estacional y la de componentes remanentes. El modelo propuesto fue probado utilizando distintas parametrizaciones para Canadá, Francia, Italia, Japón, Brasil, México y Turquía comprobándose su superioridad respecto a otros modelos como SVM y ANN con los cuales fue comparado.
1.6 Genetic FuzzySystem (GFS)
1.6.1 Largo plazo
Dalfard et al. [54] en 2013, propusieron un modelo GFS que incorporaba el efecto del aumento de los precios de energía con el fin de pronosticar el consumo anual de energía eléctrica de Irán. Como variables de entrada utilizaron la información histórica de trece años desde 1997 hasta 2009, el precio de la energía en todos los sectores económicos, el precio de gas natural en todos los sectores económicos, el GDP, la población del país, la electricidad generada por fuentes renovables y la eficiencia promedio de la generación de electricidad por medio del gas natural. Como resultado del estudio, demostraron que el modelo propuesto podría adoptarse en situaciones donde los precios de la energía aumentasen repentinamente y además se podrían extraer reglas de experto para formar una base de reglas difusa.
1.7 GreyModel (GM)
1.7.1 Largo plazo
Kumar y Jain [21] en 2010, evaluaron el uso de un modelo Grey-Model with Rolling Mechanism denominado GMRM para el pronóstico del consumo anual de energía eléctrica de India. Para su entrenamiento, utilizaron una matriz de consumos de energía eléctrica con cinco lags. El error de entrenamiento medido con la métrica MAPE fue de 3,4 %. Finalmente, para su evaluación hicieron dos predicciones: una para los años 2004-2005 y otra para los años 2005-2006, obteniéndose una precisión del 96,9 % y 95,1 % respectivamente y demostrando que el modelo propuesto tenía aplicación para dichos pronósticos.
En 2011 Lee y Tong [25], propusieron mejorar el modelo GM utilizando el método Residual Sign Estimation a través de la programación genética. Como datos de entrenamiento, utilizaron el consumo histórico de energía eléctrica de China desde 1990 hasta 2003 y construyeron un dataset con dos lags de consumo eléctrico. Al final compararon el modelo propuesto con otros tres como: GM (1,1), el propuesto por Hsu y Chen y un modelo de regresión lineal, a través de la métrica de error MAPE. Pudieron así verificar que el modelo propuesto era igual de preciso que el modelo de Hsu y Chen y mejor que los modelos GM (1,1) y el de regresión lineal.
1.8 Genetic Programming (GP)
1.8.1 Largo plazo
Azadeh y Tarverdian [30] en 2007, propusieron un modelo utilizando GP para pronosticar los consumos de energía mensual al que entrenaron con información histórica de consumos de energía de marzo de 1994 a febrero del 2005. A través de la métrica de error MAPE, lo compararon con otros de ANN demostrando su superioridad en la precisión de la predicción.
Un año después, Karabulut et al. [37], plantearon el uso de un modelo de GP para pronosticar el consumo anual de energía eléctrica de un área del sur de Turquía. Para su validación, construyeron dos modelos de regresión adicionales: el modelo Polynomial y el modelo Power Equation, donde a través de la métrica MSE determinaron que el modelo propuesto era superior.
Castelli et al. en 2015 [10], propusieron cuatro modelos utilizando GP con muestras pasadas de CEE y de información climática, con el objetivo de superar las falencias que en función a su investigación previa detectaron en algunos modelos, ya sea porque se detenían en un local óptimo al momento de entrenarlos o porque no manejaban la no linealidad de los datos. Como resultado, obtuvieron que el uso de un modelo híbrido en lugar de un modelo con operadores estándares aceleraba la convergencia del proceso de búsqueda sin sobreentrenar el modelo y con resultados aceptables.
1.9 Regression Model (RM)
1.9.1 Corto plazo
En 2017 Amber et al. [50], presentaron un modelo de RM para pronosticar el consumo diario de energía eléctrica de un edificio del sector universitario. Durante su desarrollo consideraron las siguientes variables: ECC, temperatura ambiente, radiación solar, humedad relativa, velocidad del viento, tipo de día y tipo de edificio. Para la validación del modelo usaron dos datasets, uno con la información de un edificio académico y el otro, con la de un edificio administrativo. Midieron la precisión con la métrica NRMSE. Los resultados obtenidos les permitieron demostrar que realmente las variables que aportaban mayor precisión eran la temperatura, el tipo de día y el tipo de edificio, ya que la velocidad del viento no aportaba diferencia en la precisión del pronóstico y en cuanto a la humedad y la radiación solar, como estaban correlacionadas con la temperatura, no era necesario incluirlas.
1.9.2 Largo plazo
Al-Garni et al. [31] en 1994, investigaron y desarrollaron un modelo de tipo RM para pronosticar los consumos mensuales de energía eléctrica de Arabia Saudita del Este. Como dataset de entrenamiento, utilizaron cinco años de historia con las siguientes variables: humedad relativa, radiación solar, temperatura, población. Para la validación del modelo propuesto realizaron un análisis residual.
En 2012 Adom y Bekoe [38], propusieron dos modelos de pronóstico de tipo RM que denominaron Partial Adjustment Model (PAM) y Autoregressive Distributed Lag Model (ADRL) para pronosticar el consumo anual de energía eléctrica para Ghana. Como variables de entrada al modelo consideraron las siguientes: EEC, GDP, GDP per cápita, grado de urbanización y eficiencia industrial. Los modelos fueron comparados con otros modelos de RM y concluyeron que, en cuanto a velocidad, el modelo PAM era el más rápido, pero en cuanto a precisión el modelo ADRL era el mejor. Además, el estudio reveló que existía una relación de equilibrio a largo plazo entre las variables de consumo de electricidad, la eficiencia de la industria, la urbanización y el GDP.
En 2014 Ardakani y Ardehali [2], desarrollaron y compararon varios modelos optimizados de regresión y ANN con el fin de determinar cómo la entrada de diferentes tipos de datos históricos afectaba los pronósticos de CEE y así poder pronosticar con ellos el consumo de energía eléctrica a largo tiempo de Irán y Estados Unidos. Los datos considerados fueron CEE y los indicadores GDP, IMP, EXP, y POP. Para optimizar las formas lineales y cuadráticas de los modelos de regresión, examinaron tres algoritmos de optimización: GD, PSO e IPSO. Concluyeron que independientemente del tipo de economía los pronósticos de CEE a largo tiempo basados en el modelo IPSO-ANN que utilizaba los datos socioeconómicos históricos eran más precisos.
1.10 Support Vector Machine (SVM)
1.10.1 Corto plazo
Petkovic et al. [53] desarrollaron en 2009, un modelo de SVM que utilizaba el algoritmo PSO en su entrenamiento para pronosticar el consumo de energía eléctrico en una empresa refinadora de petróleo. Como variables de entrada al modelo consideraron las siguientes: petróleo refinado diario, uso diario de las unidades industriales, tipo de petróleo refinado, consumos diarios de energía eléctrica y combustibles fósiles usados en el proceso de refinamiento y condiciones climáticas de la temporada. Para su evaluación y comparación, pronosticaron con varios modelos de SVM con distintos kernels con y sin el algoritmo PSO. Encontraron que los que utilizaban el algoritmo PSO mejoraban la precisión del pronóstico y, particularmente, el modelo que usaba el kernel RBF era el mejor con un error MAPE de 1,4646 %.
Jain et al. [23] en 2014, propusieron pronosticar el consumo de un edificio de la ciudad de Nueva York utilizando la información de consumos de energía eléctrica, la radiación solar y temperatura capturada por varios sensores distribuidos por todo el edificio. Como modelo de pronóstico, optaron por utilizar el método de SVM y considerar otras variables de entrada como el tipo de día (semana o fin de semana) y el seno y coseno de la hora. Para la validación del modelo, probaron distintas configuraciones combinando pronósticos cada diez minutos, por hora y diario y varios escenarios espaciales. Encontraron que la mejor combinación era pronosticar por pisos completos del edificio y con una granularidad horaria.
Zhang et al. [36] en 2016, presentan dos modelos de SVM, uno utilizaba el parámetro epsilon y el otro el parámetro nu, combinados ambos con el algoritmo DE para determinar sus parámetros de configuración y los pesos de los modelos. Usando como variable de entrada un dataset con el consumo histórico de un año de energía eléctrica de un edificio de Singapur, pronosticaron el consumo con una granularidad de treinta minutos y diaria. Para validar los dos modelos, los compararon contra otras tres variantes de modelos SVM y obtuvieron que los modelos propuestos los superaban. También pudieron observar que para el pronóstico de treinta minutos su error MAPE era 3,767 % y el valor del peso del parámetro nu era alto, mientras que para el pronóstico diario, su error MAPE era 5,843 % y el valor alto del peso epsilon.
1.10.2 Largo plazo
Los autores Zhang y Rui [48] en 2007, compararon dos modelos SVM para pronosticar el consumo de energía eléctrica anual de China. El primer modelo fue de tipo univariado y utilizaba como variable de entrada los datos históricos de consumos de energía de 1985 a 2005. Por el contrario, el segundo modelo fue de tipo multivariado y además consideró las siguientes variables de entrada: GDP per cápita, HIS y EIS. Como conclusión demostraron que el modelo que consideraba las variables socio-macroeconómicas mejoraba la precisión del pronóstico.
1.11 Híbridos (H)
1.11.1 Corto plazo
Li y Su [35] desarrollaron en 2010, un modelo híbrido denominado Genetic Algorithm-Hierarchical Adaptive Network-Based Fuzzy Inference System (GA-Hanfis), el cual utilizaba un algoritmo genético con una red jerárquica adaptativa basada en un sistema de inferencia difusa que disminuía la dimensión de las reglas base. Lo utilizaron para pronosticar el consumo diario de energía eléctrica del aire acondicionado de un hotel a partir de los datos históricos de consumo de energía eléctrica y temperatura. Para validarlo, lo compararon usando la métrica CV contra otros modelos de ANN y GFS pudiendo comprobar la superioridad de este.
Un año más tarde los autores Li et al. [28], plantearon un modelo híbrido que combinaba una ANN con un GFS para pronosticar el consumo mensual de energía eléctrica de un edificio y lo compararon contra un modelo tradicional de ANN de tipo FF con una sola capa oculta. Para la validación de este, utilizaron dos datasets con distintas variables, para el primero, temperatura, radicación solar, humedad y velocidad del viento y, el segundo solo la temperatura y la cantidad de ocupantes del edificio. Después de realizar cinco ejecuciones por cada dataset, finalmente obtuvieron que el modelo propuesto era superior y además se ejecutaba prácticamente en el mismo tiempo que el modelo de ANN.
En 2015 Lü et al. [32], propusieron un nuevo método basado en un enfoque físico-estadístico diseñado para tener en cuenta la heterogeneidad y complejidad de los edificios con el fin de mejorar la precisión del pronóstico. Dicho modelo híbrido estaba compuesto por un método físico, un modelo Arima, una SVD y un método Convex Hull de bases teóricas similares a las SVM. Compararon el modelo propuesto con dos modelos de SVM, uno lineal y otro no lineal, usando para el no lineal la función RBF. Para su entrenamiento y validación, emplearon información de cuatro edificios de Finlandia obteniendo resultados ellos satisfactorios.
1.11.2 Largo plazo
Los autores Meng et al. [41], publicaron un artículo en 2011 con un modelo híbrido que descomponía la serie de tiempo usando la técnica DWT en series de tiempos más simples. Como resultado obtuvieron una serie de tendencia pronosticada con un modelo GM y las series de frecuencia periódicas pronosticadas con un modelo ANN de tipo RBF. Finalmente unieron resultados para obtener el pronóstico mensual de consumos de energía. Como dataset de entrenamiento, tomaron la información de consumos de energía de China desde enero de 1990 hasta diciembre del 2016 obtenida del sitio web Chinese Economic and Financial Database of the China Centerfor Economic Research (CCER). También compararon el modelo propuesto con otros tres modelos utilizando las métricas de error MaxAPE, MAPE, MdAPE y GMARE, resultando ser el mejor solo para las métricas MaxAPE y MAPE.
En 2012 Zhang y Wang [45], propusieron para pronosticar el consumo de energía anual un modelo híbrido denominado FWNN, que combinaba los modelos ANN y GFS y descomponía la serie de entrada de consumos de energía en wavelets. Este modelo tenía como características su rápida convergencia al resultado, su facilidad de implementación y superior capacidad respecto al modelo GM contra el cual fue comparado utilizando la métrica MAPE.
En el mismo año Tang et al. [29], desarrollaron un modelo híbrido, que combinaba el EEMD y el LSSVR, con el fin de pronosticar los consumos mensuales de energía eléctrica nuclear de China. El modelo consistía en descomponer la serie de tiempo de CEE en series más simples y predecir dichos componentes por separado para luego obtener la composición del valor de pronóstico final. Como dataset de entrenamiento utilizaron la información obtenida de la Wind Database con los consumos de energía nuclear de China de marzo del 1993 a enero del 2010. Finalmente, evaluaron y compararon los modelos híbridos EEMD-LSSVR-ADD, EMD-LSSVR-LSSVR y EMD-LSSVR-ADD a través de las métricas RMSE y MAPE contra otros modelos tradicionales como SVR, LSVVR, ANN y Arima, obteniendo como resultado que el mejor era el modelo híbrido EMD-LSSVR-LSSVR.
Por otra parte Tang et al. [43], plantearon en el 2015 combinar el método de modelado basado en las características de los datos y utilizaron la técnica Decomposition and Ensemble para construir los modelos de pronósticos de CEE de tipo nuclear. Construyeron dos modelos, el primero usaba el conjunto de modelos Arima-LSSVR y el segundo, LVSSVR-LVSSVR. También construyeron y evaluaron los modelos Arima, FNN y LSSVR de forma individual para compararlos contra los propuestos. Como conclusión demostraron que estos eran superiores.
Barack y Sadegh [40] propusieron un modelo híbrido para pronosticar los consumos de energía anual de Irán, el cual combinaba un modelo lineal (Arima) con otro no lineal (GFS) con el fin de obtener las ventajas de ambos. Probaron tres patrones de configuración entre ambas técnicas e identificaron que el mejor patrón era el tercero, que usaba el método AdaBoost con la estructura ANFIS de Genfis3 y el algoritmo de entrenamiento BP. Además, este modelo obtuvo mejores resultados medidos con la métrica de error MSE, contra otros modelos como Single Arima, Single ANFIS, ANN, Zhang, Khashei and Bijari y Babu and Reddy.
1.12 Otros
1.12.1 Corto y largo plazo
Singh y Yassine [51], propusieron en 2018 un novedoso modelo que utilizaba minería de datos a través de análisis de patrones frecuentes en series de tiempo de energía, y una técnica de clustering no supervisada para obtener las reglas de asociación que serían el insumo y poder pronosticar los resultados utilizando un modelo de redes bayesianas. Para el entrenamiento, crearon un dataset sintético a partir del dataset real ISSDA-The Irish Social Science Data Archive con series de tiempo de consumos de energía de veintiún artefactos eléctricos de una casa con una resolución de un minuto. Para la evaluación de dicho modelo utilizaron dos datasets reales, el dataset UK-DALE con la serie de tiempos de consumos de energía de 109 artefactos eléctricos recolectado de cinco casas del sur de Inglaterra, con una resolución de tiempo de seis segundos y el dataset AMPds2-Almanac of Minutely Power con las series de tiempo de consumos de electricidad, agua y gas natural con una resolución de un minuto en un hogar residencial de Canadá desde el 2012 al 2014. Finalmente, evaluaron el modelo utilizando distintos tamaños de datasets de entrenamiento (25 %, 50 % y 75 % del total de este) tanto para el corto como largo plazo y lo compararon contra otros dos modelos que utilizaban técnicas distintas, SVM y ANN con configuración MLP obteniendo como resultado la superioridad del modelo propuesto sobre estos en todos los casos.
2. HALLAZGOS Y RESULTADOS
En esta sección se presentan diferentes análisis descriptivos obtenidos a partir de los artículos seleccionados. En la figura 2 se visualiza la distribución de los artículos por tipo de técnica/modelo de pronóstico. Como se puede apreciar, la técnica/modelo más usada es ANN seguida por los híbridos y Arima.
En la figura 3 se grafica la distribución de los artículos de acuerdo con la escala de tiempo. Permite visualizar que la mayoría de ellos corresponden a pronósticos de largo plazo.
A continuación, se presentan los resúmenes de los artículos clasificados según las siguientes características: modelos, variables utilizadas y métodos de error. En las tablas 5 y 6 se exponen los resúmenes de las características de los artículos de pronóstico de corto y largo plazo respectivamente.
Tabla 5 Resumen artículos pronósticos corto plazo.

P: Modelo propuesto - X: Modelo comparación
Fuente: elaboración propia
Tabla 6 Resumen artículos pronósticos largo plazo.

P: Modelo propuesto - X: Modelo comparación
Fuente: elaboración propia
2.1 Publicaciones y año de publicación
La figura 4 muestra la cantidad de publicaciones de artículos y su evolución por año para las diferentes escalas de tiempo de los pronósticos y para la suma de ambos, donde claramente se puede identificar que es un tema que se sigue desarrollando en la actualidad.
2.2 Modelos usados
En la tabla 7 se observa que el modelo de ANN es el más usado para la construcción de las soluciones de pronósticos, independientemente de la escala de tiempo a predecir. A este le siguen los modelos de Arima e híbridos, los cuales se usan casi con el mismo porcentaje en corto y largo plazo.
2.3 Variables de entrada
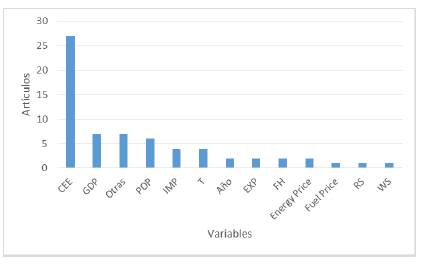
Para los pronósticos de corto y de largo plazo, la variable más utilizada es el CEE como lo indican las figuras 5 y 6 respectivamente.
2.4 Métodos/Técnicas de error
Para el cálculo de la precisión de los modelos propuestos, la técnica de error MAPE es la más utilizada (figura 7) independiente de la escala de tiempo.
3. DISCUSIÓN
Todas las soluciones propuestas en los artículos revisados se han aplicado con éxito para la predicción del CEE en sus respectivos contextos. Cada técnica posee ciertas características que deben aplicarse adecuadamente al caso de estudio.
Si bien, como muestra en la figura 3, el 60 % de los artículos revisados corresponde a pronósticos de largo plazo, cabe señalarse la tendencia creciente de artículos de corto plazo en los últimos años (figura 5), conjuntamente la tendencia creciente de ambos, lo cual muestra que el tema sigue siendo de interés para la investigación en la actualidad.
Con relación a los modelos empleados, se observa que independientemente de la escala de tiempo considerada, el ANN es el más usado debido a que tiene más ventajas que los modelos estadísticos por su versatilidad y capacidad de generar la relación de entrada y salida, sin hacer compleja la dependencia con las variables de entrada. Por su parte, los modelos basados en Arima muestran una leve preeminencia en los pronósticos de largo plazo, mientras que GFS y GM no tienen aplicación en el corto plazo. Cabe mencionar que varios autores proponen la utilización de modelos híbridos o un conjunto de modelos para superar las desventajas de cada modelo, por ejemplo, la combinación de una técnica lineal con una no lineal. Un claro ejemplo es la utilización de un modelo ANN con un algoritmo que ayuda a calcular los pesos iniciales de los nodos, evitando que queden en un mínimo local y que resulten de convergencia lenta. Es importante resaltar que, aunque las ANN sean el modelo más utilizado en los artículos revisados, no es suficiente evidencia para afirmar que es el mejor, debido a que en las contrastaciones, debería utilizarse el mismo conjunto de datos y, al mismo tiempo, medirse la precisión de los resultados utilizando la misma técnica para el cálculo del error. Otras diferencias que se evidencian es el no uso de las mismas técnicas/modelos en las distintas escalas de tiempo y que el método Arima solo aplica para pronósticos de tipo univariados.
Respecto a las variables de entrada, la más utilizada en todas las soluciones propuestas independientemente de sus características específicas es el CEE. A fin de redundar en mejores resultados, en los estudios de corto plazo la variable complementaria de mayor recurrencia es la temperatura, mientras que en los de largo plazo lo son las variables macroeconómicas como GDP y POP.
Si bien mayoritariamente el error es medido con MAPE, en un 60 % de los artículos se implementó un conjunto de otras técnicas, tales como RSME, MSE y MAE, para dar mayor fiabilidad y validación a los modelos.
Finalmente, la metodología de investigación/trabajo se basó mayoritariamente en casos de estudio aplicados, debido a la importancia actual de poder contar con una herramienta de pronóstico para resolver los distintos problemas planteados.
4. CONCLUSIONES
En este trabajo se revisaron artículos de la literatura sobre propuestas de modelos de pronósticos para el CEE, donde se identificaron las ventajas y desventajas en cada uno de ellos según se tratase de pronósticos a corto o largo plazo. Entre estas técnicas/ modelos, las ANN han ganado la mayor atención de numerosos investigadores debido a su precisión y simplicidad en la construcción. Sin embargo, varios autores proponen tanto modelos híbridos como nuevos que buscan mejorar aún más la precisión de los pronósticos de forma simultánea con la adaptabilidad de este a los cambios de comportamiento de los consumidores de energía eléctrica y la adecuada selección de variables de entrada. Otro punto de importancia es la selección de variables de entrada y su cantidad a ser considerada. En último lugar, se registra la importancia de contar con métricas de cálculo de error como MAPE, ya sea solo o con otras métricas para validar, evaluar y determinar el modelo más efectivo.
A partir del conocimiento obtenido a través de la revisión realizada, se propone como línea de investigación la profundización de modelos para el pronóstico de CEE a corto plazo para un país latinoamericano en vías de desarrollo, comparando y evaluando diferentes técnicas/modelos, variables y herramientas ya existentes con el objetivo proponer el modelo que provea información precisa y confiable para la toma de decisiones a los distintos participantes de la cadena constitutiva del mercado eléctrico, con relación a la planeación y optimización de recursos y preservación del medio ambiente.