1. INTRODUCCIÓN
La cooperación hace que los seres vivos se desenvuelvan en distintos escenarios de manera eficiente, estos aprovechan sus capacidades para llevar a cabo una serie de tareas que les permiten alcanzar un objetivo común al grupo [2]. El propósito de resolver tareas de forma conjunta se debe al aumento de complejidad que estas presentan cuando solo un individuo intenta resolverlas. Esta es la base sobre la cual se fundamentan los sistemas multi-agente [3]. En particular, es importante dirigir las prestaciones de los sistemas multi-agente al desarrollo de problemas que conlleven a un mejor uso de los recursos que sostienen la vida en nuestro planeta.
El estudio de los sistemas multi-agente es de gran interés debido a las prestaciones que estos pueden ofrecer en ciertas tareas [4]: (i) tareas que son muy complejas para llevar a cabo por parte de un solo robot o simplemente porque el hecho de usar varios robots puede presentar una mayor utilidad, por ejemplo, tareas de exploración de ambientes, (ii) construir y usar varios robots simples puede ser más económico, más fácil, más flexible, y sobretodo más tolerante a fallas que usar un único súper robot, (iii) el campo de aplicación de los resultados encontrados usando múltiples robots puede ser extendido a otras áreas de estudio como las ciencias sociales.
Aquí, el problema abordado hace referencia a tareas de vigilancia y monitoreo en un terreno determinado, este problema es conocido como surveillance [5], en el cual, agentes autónomos siguiendo reglas simples y exhibiendo una conducta cooperativa, se distribuyen de manera eficiente en un terreno para desarrollar acciones sobre puntos espaciales del mismo; el uso de un sistema multi-agente se debe al aprovechamiento de las capacidades de este tipo de sistemas a la hora de desarrollar tareas complejas.
2. TEORÍA
2.1 Sistemas multi-agente y control cooperativo
Un agente es un sistema computacional o una entidad dinámica creada para llevar a cabo un conjunto de tareas en un complejo ambiente dinámico, dependiendo del tipo de hábitat que el agente ocupe, este puede tomar una forma determinada, así, si el agente está sumergido en un mundo físico, entonces típicamente el agente es un robot [6]. Un sistema con múltiples agentes es un equipo de agentes donde cada uno interactúa con los demás agentes y su ambiente, para tomar decisiones que le permitan realizar una tarea específica y finalmente cumplir con un objetivo común al grupo.
El objetivo de trabajar con sistemas multi-agente es encontrar métodos que permitan que aun cuando cada agente solo opera con conocimiento local y con capacidades limitadas, el resultado sea una conducta global deseada que permita cumplir un objetivo.
La cooperación en los sistemas multi-agente es uno de los verdaderos retos que se afrontan en la implementación de estos sistemas, esta conducta cooperativa es la que debe emerger en un sistema con el ánimo de ofrecer un alto grado de confianza en el desarrollo de misiones totalmente autónomas, este tipo de tareas pueden ser resueltas eficazmente aprovechando el verdadero potencial que ofrecen los sistema multi-agente, siendo una gran cualidad que no están limitados espacialmente; además, como son varias entidades resolviendo un problema global entonces cada una puede abordar un objetivo específico de acuerdo a sus capacidades logrando que el tiempo total empleado para resolver la tarea encomendada se reduzca, y por otra parte, el hecho que un agente se vea afectado por alguna circunstancia y no pueda continuar, no quiere decir que la tarea deba cancelarse.
Es importante resaltar que para la implementación de este tipo de sistemas donde se hace necesario que surja una conducta cooperativa, debe haber una buena toma de decisiones, es decir, saber qué acciones deberá llevar a cabo un agente teniendo en cuenta el estado de sus compañeros y la información del ambiente que le es proporcionada a través de sus sensores, toda esta información es procesada y evaluada mediante la integración de técnicas derivadas de otras áreas de estudio tales como la teoría de juegos, la economía, la biología y la inteligencia artificial [7].
2.2 Forrajeo
Es el proceso mediante el cual los animales buscan comida, es un área de estudio del comportamiento animal, que se basa principalmente en la utilidad o beneficio que un animal obtiene al implementar un método de búsqueda de alimento [8], con el fin de maximizar una función que dependa de la energía E que le brindan los nutrientes que adquiere y el tiempo T que invierte buscándolos, la cual se puede expresar como E/T [2]. Un amplio panorama de la teoría de forrajeo se puede encontrar en [9].
En el marco de la robótica móvil, el forrajeo es el proceso en el cual, un grupo de robots debe llevar a cabo alguna acción sobre objetos encontrados en el ambiente con el cual interactúan [4], esta es una tarea que hace referencia a muchos campos de aplicación de sistemas multi-agente como limpieza, detección de minas antipersonas, operaciones de búsqueda y rescate, etc., residuos tóxicos, trabajos de recolección de frutos en cultivos.
2.3 IFD (Ideal Free Distribution) y load balancing
El concepto de Ideal Free Disribution fue introducido originalmente por Fretwell en [10], donde se desarrolla un estudio sobre los factores que afectan la distribución de aves en determinados hábitats. La idea del IFD involucra dos conceptos claves:
Habitat : el hábitat de una especie es una porción de la superficie de la tierra en la cual esta puede vivir. El área total de un hábitat disponible para una especie puede ser dividida en diferentes regiones, donde el tamaño de cada región, las cuales no necesariamente deben ser iguales y tampoco contiguas. Como en cada región puede haber un determinado número de individuos de la especie, entonces cada región tendrá una densidad, la cual depende de su área y del número de individuos que la ocupan.
Suitability : la selección del hábitat que un individuo ocupará es un fenómeno que involucra estímulos y respuestas, esto quiere decir que un individuo ocupará una determinada región a partir de la oportunidad de supervivencia que esta le brinda “suitability”, esta medida de conveniencia podría ser determinada por factores como, la tasa a la cual un individuo consigue alimento y la cantidad potencial de depredadores que podrían aparecer en su hábitat.
En el concepto de distribución ideal libre, el término “ideal” significa que cada individuo puede sensar perfectamente la “suitability” de cada región, y de esta manera escoger la región que le brinda una mayor oportunidad de éxito, y el término “free” significa que los individuos se pueden mover hacia cualquier región.
Load balancing: es una técnica que permite trabajar con sistemas multi-agente para que estos desarrollen tareas acordes a sus capacidades, evitando que un agente tenga sobre carga de funciones mientras que otros se encuentran sin realizar tareas, algunos trabajos en los que se implementa se pueden ver en [11], [12] y [13] donde se realizan esquemas de control para asignación de recursos, y sistemas de control automático; otro trabajo en el que utilizan la técnica de load balancing para realizar la asignación de potencia eléctrica a una red de distribución de energía se encuentra en [14], otros trabajos en los cuales se realizan el balance de carga de servidores de internet y computación en paralelo se puede apreciar en [15] y [16].
El objetivo de combinar el concepto de la distribución ideal libre junto con la herramienta de load balancing en este trabajo, es desarrollar un mecanismo que permita que un grupo de robots explore de manera eficiente un determinado terreno, mediante el cual, los agentes compartan información y puedan alcanzar una distribución espacial mediante reglas que definen su comportamiento de tal manera que emerja una conducta cooperativa.
2.4 Diagramas de Voronoi
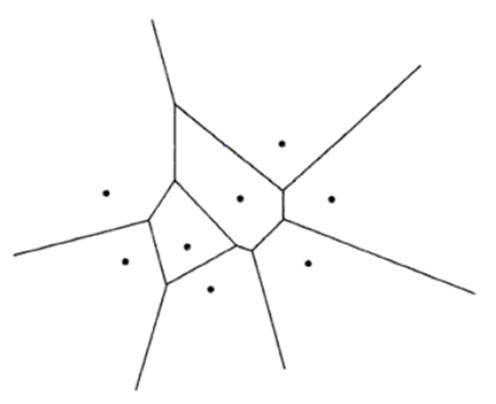
Un diagrama de Voronoi es una construcción geométrica que permite realizar una partición del espacio a partir de una serie de puntos dados, ver figura 1. El diagrama de Voronoi divide el espacio acorde a la regla del vecino más cercano donde cada punto es asociado con la región del espacio que este más próxima a él.
Matemáticamente, un diagrama de Voronoi se puede definir como: denotemos P: = {p1, p2,…, pn} como el conjunto de n puntos distintos en el plano; estos puntos son llamados sitios. El diagrama de Voronoi del conjunto de sitios P se define como la subdivisión del plano en n celdas, una para cada sitio en P con la propiedad que un punto z se encuentra en la celda correspondiente al sitio Pi si y solo sí 𝛿 (𝑧, 𝑝i) < 𝛿 (𝑧, 𝑝j) para cada pj ∈ 𝑃 | 𝑗 ≠ 𝑖 donde 𝛿 (𝑧, 𝑝) = Así, el dominio del sitio Pi sobre el sitio Pj estaría dado por 𝑑𝑜m (𝑝i, 𝑝j) = 𝑧 ∈ 𝑅2 | 𝛿 (𝑧, 𝑝i) ≤ 𝛿(𝑧, 𝑝j)}.
En robótica, la mayoría de los trabajos que emplean diagramas de Voronoi, los utilizan para generar una ruta o un camino deseado.
3. METODOLOGÍA
El modelo desarrollado del sistema multi-agente para llevar a cabo la tarea de forrajeo, es evaluado en un terreno simulado como un cultivo de plantas que sufre la infección de un hongo fitopatógeno; está aplicación se desarrolla con el ánimo de simular una posible solución a problemas agrícolas, como en el estudio de Grift (2007), donde un grupo de robots realiza las tareas necesarias para mantener la producción de un determinado cultivo. El modelo de difusión del hongo fitopatógeno se implementó en un trabajo previo el cual se puede ver en [17].
3.1 Modelo del sistema multi-agente
El modelo del sistema multi-agente desarrollado presenta un aporte experimental al trabajo realizado en (1), y está muy ligado a los trabajos presentados en [18], [19] y [20] para balance de carga discreta.
3.1.1 Suitability
Los agentes están equipados con un sensor isotrópico de radio rfp , con el cual detectan las plantas infectadas en el cultivo. Inicialmente, estos entran a trabajar en un cultivo que virtualmente se ha dividido en diferentes regiones mediante un diagrama de Voronoi. El diagrama de Voronoi divide el cultivo en R regiones, cada región i=1,2,…R tiene asociada una suitability Si (ni,Ai) con base en la cual los agentes tomarán la decisión de permanecer o no en una determinada región. Siendo ni el número de agentes que están en la región i, y Ai y el área de la región i. Además, ni ≥ mr donde mr representa la mínima cantidad de agentes que deben estar en una región. Por otra parte, la cantidad total de agentes T en el cultivo se mantiene constante, siendo T=∑R ni . La suitability de una región Si será directamente proporcional a su área Ai , e inversamente proporcional a la cantidad de agentes ni que la ocupen, esto garantiza que los robots se distribuyan en todas las regiones (load balancing) sin dar lugar a que se produzcan hacinamientos. Como el área Ai de las regiones permanece constante, la suitability de una región solo cambiará cuando haya una entrada o salida de agentes en la región. La suitability de una región i se define en este trabajo como:
La cual depende del área de la región i dada por Ai y de la cantidad de agentes ni que se encuentren en la región.
3.1.2 Restricciones territoriales de sensado y traslado
Las conexiones que se construyen a partir del diagrama de Voronoi se modelan mediante un grafo (H,C) donde H={1,…R} y C⊂H × H. Con esto, si (i,j) ∈ C con (i ≠j) significa que la región i y la región j son contiguas, así, los agentes que están en la región j pueden sensar la suitability de la región j Si y trasladarse a ella si les conviene. De igual manera, los agentes de la región j también pueden sensar y trasladarse a la región. Es necesario que para cada i ∈ H exista un tal j ∈H que (i,j) ∈C asegurando que todas las regiones tendrán al menos una región contigua. De esta manera, los agentes podrán ocupar cualquier región mediante el paso intermedio a través de distintas regiones. La evolución de este sistema multi-agente se representa mediante la siguiente ecuación, siendo Υ+=(mr,inf):
De esta manera, X representa el conjunto de todos los estados posibles en los que se encuentra el sistema multi-agente, donde un estado muestra cómo están distribuidos en las regiones, los agentes en un instante k es decir, que n(k) ∈ X para todo k ≥ 0 donde n(k)=( n1 (k) ,n2 (k) ,…,nn (k) ) ∈ X es el vector de estado, y ni (k) indica el número de agentes que están en la región i en el instante k. A diferencia del trabajo realizado en (18), aquí se asume que el número de robots exploradores no necesariamente debe ser muy grande y por lo tanto el paso de carga (cambio de región de un agente) se representa mediante una variable discreta.
3.2 Interacción con el ambiente
Según el trabajo previo realizado en (17), el modelo del sistema multi-agente en su interacción con el ambiente comprendía dos estados, explorando, y trasladando, para lo cual solo era necesario que el agente conociera el estado de un agente j que interfiriera en su rango de búsqueda. En este trabajo, se adiciona un nuevo estado el cual denominaremos cambio de región. En este sentido, para un agente la prioridad es situarse en la región que tenga una mayor suitability, y a partir de ese momento, realizar la búsqueda de plantas infectadas de igual manera que los agentes exploradores en el trabajo presentado en [17].
Consideremos ahora un conjunto de eventos E y un evento, el cual representa la posibilidad que un determinado número de agentes se están moviendo desde la región i ∈ H hacia regiones vecinas m ∈ p(i), donde p(i) representa los vecinos de la región i, p(i) = {j(i,j)∈C}. Se denota a αm (i) como la cantidad de agentes que se mueven de la región i ∈H a la región m ∈p(i) y que α(i)=( αj (i): j ∈ p(i)). En este sentido, se alcanzará un estado en el que a ningún agente le conviene cambiar de región cuando todas las suitabilities de las regiones sean iguales Si=Sj |i ∈ H o cuando αm (i) = 0|i ∈ H, es decir, cuando ningún agente se encuentre en estado de cambio de región. El estado cambio de nodo depende de la suitability Si de la región en la que se encuentre el agente y de la suitability de sus regiones vecinas; de esta manera, el estado cambio de nodo queda definido mediante las siguientes condiciones:
Si Si > Sj αj (i) = 0 , donde j ∈ p(i), esta condición implica que el número de agentes de la región i que determinan pasarse a la región j es cero, si las suitabilities de ambas regiones son iguales, o si la suitabilty de la región i es mayor que la suitability de la región j.
Si una región i tiene varios vecinos, entonces un agente establecerá su posible destino como la región vecina que tenga la mayor suitability.
Una vez establecida cual es la región que tiene la mayor suitability, este decidirá trasladarse a ella si su suitability será mejor aún que la que le brinda la región que ocupa actualmente.
Cuando un agente no se encuentra en el estado cambio de región, entonces este realizará su tarea de igual manera que los agentes exploradores según el trabajo en [17], donde el proceso de forrajeo se llevará a cabo en la región en la que encontró una mayor suitability.
4. RESULTADOS Y DISCUSIÓN
Los resultados que se muestran a continuación se obtuvieron a través de la simulación en un escenario dado por un terreno de 80 x 80 metros, el cual había sufrido una infección producida por hongos fitopatógenos. La operación de los agentes comienza en un terreno previamente dividido mediante un diagrama de Voronoi (ver figura 2), momento en el cual analizan si deberían cambiar de región con el fin de obtener una mejor suitability. Estos resultados de simulaciones corresponden a múltiples pruebas bajo el mismo escenario, se trabajó en el cultivo que se muestra en la figura 2, el cual de un total de 6400 plantas, 1493 se encuentran infectadas.

Figura 2 Partición de un terreno de 80 x 80 metros. El cultivo se dividió en cinco regiones donde solo una está conectada con todas. Los puntos representan plantas infectadas, y los círculos corresponden a los centroides de esas concentraciones.
La figura 3 representa el conjunto de tres posibles conjuntos de estados por los que pasa un equipo de 25 agentes hasta alcanzar un estado en el que a ningún agente le conviene cambiar de región. La figura 3 permite ver la evolución de la suitability de cada región a partir del movimiento de los agentes en el terreno dividido mediante un diagrama de Voronoi, aquí es posible evidenciar el efecto del uso de la estrategia de load balancing, con la cual, a través de la conducta cooperativa que exhiben los agentes estos se establecen la región en la cual deberían llevar a cabo la tarea de búsqueda.

Figura 3 Tres conjuntos de estados para un terreno dividido en cinco regiones, donde se logra una misma distribución de agentes.
En las figuras 4 y 5, se pueden ver los resultados de un experimento en el cual se fumigan plantas infectadas acorde a dos estrategias, sin balancear los niveles de suitability (No IFD), y balanceando los niveles de suitability (IFD), se trabajó con 5 cantidades de robots, 5, 10, 15, 20, y 25, es posible apreciar que con la estrategia de balancear los niveles de suitability, el número de plantas fumigadas es mayor que sin realizar el balance; además, con la estrategia de balancear los niveles de suitability, la cantidad de plantas fumigadas tiene una mayor concentración; los resultados de la simulación apreciados en la figura 4 corresponden a 500, 1000, 1500, y 2000 pasos ejecutados por los agentes, y en la figura 5 corresponden a 2500, 3000, 3500, y 4000 pasos ejecutados por los agentes. finalmente, se puede ver que a mayor número de agentes trabajando en el terreno del cultivo, mayor es el número de plantas fumigadas en ambas estrategias.

Figura 4 Mediana de la cantidad de plantas fumigadas por los agentes bajo dos estrategias, sin balancear (No IFD) y balanceando los niveles de suitability (IFD) Versión 1.

Figura 5 Mediana de la cantidad de plantas fumigadas por los agentes bajo dos estrategias, sin balancear (No IFD) y balanceando los niveles de suitability (IFD) Versión 2.
En particular, el experimento llevado a cabo para 15 agentes con distintos pasos de operación se presenta en la figura 6, donde a través de un diagrama de cajas podemos ver la efectividad de usar la estrategia de balance de suitability, la cual refleja siempre una mayor cantidad de plantas fumigadas con respecto a la estrategia en la cual no se realiza balance de suitability.

Figura 6 Experimento realizado para 15 agentes con distintos pasos de operación bajo dos estrategias, sin balancear (No IFD) y balanceando los niveles de suitability (IFD).
Finalmente, en la figura 7 se presenta la gráfica de la mediana de los puntos fumigados bajo ambas estrategias, (No IFD, línea azul) y (IFD, línea roja), de donde podemos corroborar la eficiencia de la estrategia IFD; además, para una pequeña cantidad de agentes, la estrategia IFD presenta unos beneficios significativamente mejores en cuanto a las plantas fumigadas.
5. CONCLUSIONES
Se desarrolló y simuló un modelo de sistema multi-agente para realizar la tarea de forrajeo con el objetivo de erradicar la enfermedad producida por un hongo fitopatógeno en un cultivo, los agentes demostraron una conducta cooperativa en el desarrollo de la tarea y a partir de regla simples y con conocimiento local del estado de sus compañeros de demostró a través de simulaciones que estos pudieron distribuirse en un terreno para cubrirlo de forma eficiente.
La partición del terreno se lleva a cabo con el fin de modelar al sistema multi-agente bajo la idea de la distribución ideal libre (IFD) y load balancing, en la que a cada región definida por el diagrama de Voronoi le corresponde una cantidad de agentes acorde a su área.
Se define una medida de conveniencia para cada región conocida como suitability, la cual aumenta cuando disminuye la cantidad de robots presente en esa región y disminuye en caso contrario, así, los agentes deben balancear los niveles de suitability con el fin que cada región sea explorada de manera eficiente y no haya sobre carga de agentes.
Particularmente, bajo las pruebas simuladas, se puede apreciar que la cantidad de puntos fumigados es mayor cuando la estrategia de los agentes es balancear los niveles de suitability (IFD), que cuando estos trabajan sin realizar partición del terreno, aun así, ambos comportamientos exhiben una conducta cooperativa.