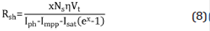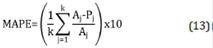1. Introducción
La generación de energía eléctrica utilizando tecnología solar fotovoltaica (PV ) ha mostrado un crecimiento significativo en los últimos años (Intersolar Europe, Global Solar Council (GSC), 2018); es así como a 2018 se tiene una capacidad instalada de 505,2 GW alrededor del mundo. La consolidación de los sistemas PV como una opción competitiva para la generación de energía eléctrica trae consigo nuevos retos en investigación para lograr una mejor operación de este tipo de sistemas garantizando su confiabilidad y sostenibilidad. Uno de los problemas asociados a la operación de sistemas PV es la degradación de los paneles solares; las diferentes condiciones ambientales de radiación, velocidad de viento, temperatura, lluvia, polvo, entre otros, a los que los paneles están expuestos afectan su producción energética (Tudor Cotfas, et al., 2018).
Por tanto, el monitoreo del estado de operación de los paneles que forman un sistema PV es una tarea fundamental; dicho monitoreo se puede realizar a través de diferentes técnicas ampliamente reportadas en la literatura, una de ellas es la termografía infrarroja, mediante la cual generalmente se logran detectar puntos calientes o “hot spots” y también posibles defectos estructurales causados por temperaturas elevadas (Fadhel, et al., 2019); la principal desventaja de esta técnica es que implica tener equipo especializado que puede resultar costoso. Otras técnicas están basadas en la comparación entre mediciones y valores analíticos calculados a través de simulación (Santiago, et al., 2013); en (Silvestre & Chouder, 2010) y (Chine, et al., 2014) se compara el valor de potencia obtenido en simulación de Matlab-Simulink con la potencia medida para detectar posibles fallas y degradación. Finalmente, existen otras técnicas que se basan en la obtención y análisis de las curvas I-V de los arreglos; estas técnicas pueden proveer más información que las basadas solo en mediciones de potencia ya que las curvas I-V de los arreglos y módulos PV contienen información relacionada directamente con su funcionamiento y estado. La corriente de corto circuito (Isc), el voltaje de circuito abierto (Voc) y el punto de máxima potencia (Vm,Im) son puntos de referencia que tienen información sobre el estado del panel. En (Pei & Hao, 2019) se propone definir indicadores de voltaje y tensión y ciertos umbrales que indiquen anormalidades; luego la detección de la degradación se hace a partir de las mediciones experimentales y los valores de los umbrales definidos. Por otro lado, en (Fadhel, et al., 2019) se introduce un método de identificación de fallas basado en la extracción de parámetros de la curva I-V y en el análisis de componentes principales (PCA). Otros trabajos reportados en la literatura utilizan parámetros como la corriente de corto circuito (Isc), el voltaje de circuito abierto (Voc) y el punto de máxima potencia (Vm,Im) como las entradas de algoritmos de inteligencia artificial o aprendizaje de máquina (Li, et al., 2019) para estudiar en detalle el comportamiento del arreglo y las posibles condiciones de degradación o fallas. Sin embargo, a pesar de la precisión de estos métodos, la complejidad de los algoritmos y el costo computacional puede ser una desventaja a la hora de implementarlos en aplicaciones reales.
Junto con los parámetros mencionados anterior mente (Isc, Voc, Vm, Im), el Factor de Forma o Fill Factor (FF) es un indicador de la degradación de un panel solar ya que, como se describe en (1), el FF depende de los cambios del voltaje y de la corriente, y varía según el nivel de radiación solar recibido por el panel. Por tanto, bajo condiciones de sombreado parcial o fallo se puede dar una disminución significativa del FF. Bajo condiciones STC, el FF sin fallas está entre 0.7 y 0.75; cuando el valor de FF es menor que 0.7, puede decirse que el panel se encuentra en un estado de degradación o que ha ocurrido una falla. Finalmente, cuando el FF es menor que 0.6, puede determinarse una falla seria (PV Education, 2013).
Aunque el FF puede indicar degradación, es mayormente utilizado como una medida del buen comportamiento de un sistema PV en forma general. En trabajos como (Bingöl & Özkaya, 2018), (Vijayalekshmy, et al., 2016) and (Chen, et al., 2016) el FF se utiliza para evaluar el desempeño de diferentes configuraciones de arreglos PV operando bajo condiciones de sombreado parcial. Por otro lado, en (Bastidas-Rodriguez, et al., 2017) el FF se utiliza un indicador denominado FF normalizado el cual corresponde a la relación del FF en una condición de operación determinada y el FF en condiciones estándar o STC; este indicador permite cuantificar la degradación debido a los cambios que pueden presentar se en el MPP cuando los paneles se degradan. El método es aplicado a nivel de panel, debido a esto no se explora el comportamiento de la condición de degradación cuando un arreglo opera con sombreado parcial. Del contexto descrito se detecta que el FF se ha utilizado como indicador de las variaciones del MPP en arreglos con sombreado parcial, pero no se ha aso ciado a la degradación de los paneles que componen el arreglo. El análisis del FF para medir la degradación ha sido utilizado a nivel de panel, pero no se ha explorado su uso en arreglos bajo radiación uniforme o bajo som breado parcial. Por tanto, en este artículo se presenta un estudio del comportamiento del FF en arreglos PV con degradación operando bajo condiciones de sombreado parcial. El análisis presentado se basa en la simulación de arreglos de diferente tamaño expuestos a diferentes niveles de degradación, posición del panel degradado y diferentes perfiles de sombreado. Para llevar a cabo las simulaciones se utilizó el modelo de un diodo y se adoptó el procedimiento descrito en (Bastidas-Rodriguez, et al., 2018) para obtener las curvas I-V y P-V.
El artículo está organizado de la siguiente forma : en la sección Materiales y Métodos se describe el efecto de la degradación en el modelo circuital de un diodo tomando como base los conceptos introducidos en (Bastidas-Rodriguez, et al., 2017); de igual forma en esta sección presenta el procedimiento matemático para obtener las curvas I-V y P-V tomando como base el procedimiento presentado en (Bastidas-Rodriguez, et al., 2018). Finalmente, en las secciones Resultados y Discusión se presentan las simulaciones de los dife rentes casos considerados en este trabajo y el análisis de las mismas.
2. Materiales y Métodos
Técnicas para cuantificar el índice de degradación
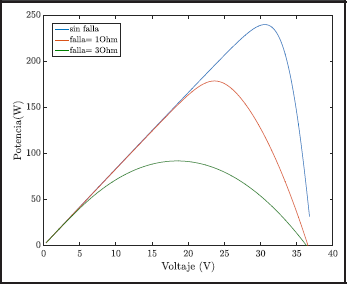
En cualquier tipo de instalación fotovoltaica deben realizarse medidas de monitoreo y análisis del nivel de degradación de los módulos del arreglo PV, esto para tener un registro de la energía que suministran los módulos a través del tiempo. En la literatura, las diferentes técnicas de cuantificación de la degradación en módulos PV se encuentran bien reportadas, sin embargo, para arreglos PV la información presente en la literatura no es precisamente descriptiva en cuanto a métodos o técnicas para hallar el nivel de degradación del conjunto de módulos cuando operan bajo condiciones de sombreado parcial. Análisis como el descrito en (Amornrat et al., 2017) utilizan una tasa de desempeño que considera el rendimiento del arreglo PV y el rendimiento de referencia con irradiación a valor STC (i.e 1000 W⁄m2) para obtener el porcentaje de degradación mensual y mediante un análisis estadístico de los datos tomados en 4 años, se obtiene la tendencia de degradación de los módulos del arreglo PV con un método de regresión lineal, sin embargo, no consideran el impacto de los parámetros que describen el comportamiento eléctrico de los módulos, así como el FF. Por otra parte, los autores de (Spertino, et al., 2014) realizan un proceso de identificación de fallas en el arreglo PV mediante la medición de los perfiles I-V en donde se presentan la falla o la caída de potencia suministrada, sin embargo no consideran el arreglo PV con sombreado parcial o su nivel de envejecimiento. El procedimiento descrito en (Bastidas-Rodriguez, et al., 2017) permite cuantificar el nivel de degradación de un módulo PV con dos indicadores: los cambios es la resistencia en serie δRs y la resistencia en paralelo δRsh , las cuales son afectadas por diferentes fuentes de degradación y se consideran como las variables que afectan directamente la reducción del Punto de Máxima Potencia (MPP, Maximum Power Point). Tal situación se ilustra en la Figura 1, donde se muestran diferentes curvas P-V de un módulo expuesto a diferentes niveles de degradación. Sin embargo, el procedimiento para cuantificar la degradación de un módulo PV no es preci- so para medir el nivel de degradación de un arreglo PV al presentar diferentes condiciones de operación como las condiciones no uniformes de irradiación (e.g sombreado parcial); debido a la activación de los diodos de bypass, en el perfil P-V pueden identificarse un Punto de Máxima Potencia Global (GMMP, Global Maximum Power Point) y uno o varios Puntos de Máxima Potencia Local (LMPP, Local Maximum Power Point). Dependiendo del nivel de degradación y de la radiación incidente en el panel, se pueden presentar diferentes situaciones.
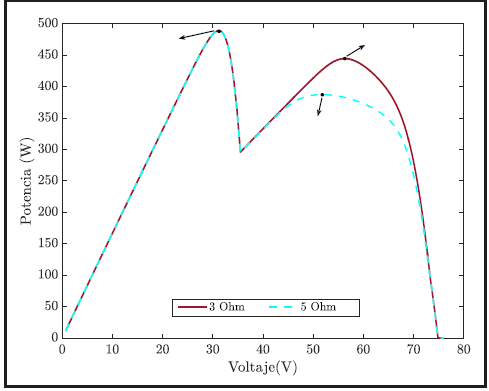
Por ejemplo, en la Figura 2, la curva punteada representa el perfil de potencia de un arreglo SP 2x2 operando con dos niveles de radiación 1000 W/m2 y 500 W/m2 lo que ocasiona que la curva tenga dos puntos máximos de potencia, GMPP = 444.5 W y LMPP = 375.3 W. Uno de los paneles expuesto a 1000 W/m2 tiene un nivel de degradación correspondiente a Rs=3Ω, esto ocasiona una leve deformación de la curva en la vecindad del GMPP. Por otro lado, la curva continúa presenta el perfil de potencia del mismo arreglo expuesto al mismo perfil de radiación pero esta vez simulando un nivel de degradación correspondiente a Rs=5Ω en el mismo panel; estas condiciones de operación ocasionan un cambio drástico en el valor del GMPP que pasa a ser 387.3 W, mientras el LMPP permaneció igual. Si se analiza la degradación del panel utilizando el cambio en el FF se podrá evidenciar el cambio en el comportamiento ya que la degradación afectó directamente el comportamiento del GMPP.
La Figura 3 muestra los perfiles P-V del mismo arreglo SP 2x2 con el mismo perfil de sombreado pero con una degradación correspondiente a Rs=3Ω aplicada a un panel expuesto a 1000 W/m2 (línea punteada) y con una degradación correspondiente a Rs=5Ω (línea continua). A diferencia del caso anterior, el cambio se da en el LMPP que pasa de 444.5 W para el primer caso de degradación a 387.3 W para el segundo; el GMPP permanece constante en 488.8 W para las dos condiciones de degradación. En este caso, si se utiliza el FF como medida de la degradación se estaría realizando una medida incorrecta ya que el efecto de la degradación no afecta el GMPP.
Por tanto, para poder hacer un análisis de la degradación es necesario incluir el comportamiento de los LMPP del arreglo, es decir, es necesario tener en cuenta el perfil de sombreado parcial que afecta el arreglo ya que de este depende la cantidad de puntos de máxima potencia de la curva P-V. En este trabajo se busca analizar a través de perfiles P-V de un arreglo PV el nivel de degradación del mismo, manipulando la resistencia en serie Rs, tomando como punto de partida el método realizado en (Bastidas-Rodriguez, et al., 2017) para estudiar su impacto en los módulos dependiendo de las condiciones ambientales.
Técnica de análisis de degradación de arreglo PV
El análisis y cuantificación de nivel de degradación no solo en módulos sino en arreglos PV es una herramienta que le permite a los usuarios de los sistemas PV estar al tanto de la eficiencia que su sistema tiene a través del tiempo. No obstante, esta puede ser una tarea dispendiosa y que puede generar altos costos, de igual manera, pueden utilizarse herramientas de simulación tales como Simulink, o PSIM, pero a la hora de tener instalaciones PV de gran tamaño, estas herramientas pasan a ser muy poco útiles. En este artículo se utiliza el procedimiento descrito en (Bastidas-Rodriguez, et al., 2018) el cual es adecuado para analizar arreglos de tamaño NxM (N filas, M columnas) y con los parámetros δRs y δRsh de simulación de degradación utilizados en (Bastidas-Rodriguez, et al., 2017), puede mostrarse el efecto de la degradación en arreglos PV.
El algoritmo descrito en (Bastidas-Rodriguez, et al., 2018) modela el comportamiento eléctrico de un arreglo PV de tamaño NxM conectado con cualquier tipo de configuración, es decir, regular (e.g. SP, TCT o BL) o irregular, operando bajo condiciones ambientales uniformes o de sombreado parcial, esto se realiza para obtener las características de corriente y voltaje (I-V) y, por ende, el perfil de potencia y voltaje (P-V). La relación I-V descrita por el modelo de un solo diodo (SDM, Single Diode Model) se encuentra en (2), el cual es amplia mente utilizado en la literatura debido a que presenta una buena relación entre simplicidad y precisión. Las ecuaciones reportadas en (Accarino, et al., 2013) y (De Soto, et al., 2006) describen la solución del conjunto de ecuaciones por medio del método de Lambert W, de los 5 parámetros que conforman el SDM, las cuales son depen dientes de la irradiación G y de la temperatura T, luego, ambas variables deben proveerse para cada uno de los módulos del arreglo PV para obtener las características I-V de manera apropiada, ya que el asumir igualdad de condiciones en los módulos PV puede llevarse a impre cisiones en la predicción de la potencia suministrada por el arreglo PV, es por esto que el algoritmo reportado en (Bastidas-Rodriguez, et al., 2018) se modificó de tal manera que las ecuaciones sean calculadas para cada uno de los módulos del arreglo PV. Las Ecuaciones (3) y (4) corresponden a la Banda GAP del Silicio en el cual los parámetros de ajuste son Eg (0) =1.166 eV, α = 0.473 meV/K y β =636 K (De Soto, et al., 2006) y el factor de idealidad del diodo respectivamente. La Ecuación (5) describe la corriente de saturación del diodo, donde la constante de Botzman K=1.38065*10-23 J/K, la carga del electrón q = 1.602176 *10-19 C y T la temperatura ambiente que recibe el módulo en grados K.
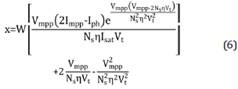
Con el cambio de variable se simplifican las ecuaciones no lineales cuya forma explícita se encuentra en (6), esto para encontrar la resistencia en serie Rs de (7) y la resistencia en paralelo Rsh de (8).
Para el cálculo de la corriente fotovoltaica Iph presentada en (9), donde αIsc corresponde al coeficiente de temperatura de corriente, TSTC = 298 K, GSTC =1000 W⁄m2 , se parte de la premisa que la corriente fotovoltaica a condiciones estándar de prueba (STC ) es aproximadamente igual a la corriente de corto-circuito (Isc, STC) dada por el fabricante:
Para tener en cuenta el perfil de irradiación del arreglo PV se hace uso de una matriz de tamaño NxM denominada matriz de mismatching, la cual describe el perfil de sombreado, representando con valores entre 0 y 1 el porcentaje del área sombreada de cada módulo, en donde, 0 se relaciona con 0% de sombreado, es decir, el módulo no tiene sombra y 1, con 100% de sombreado, es decir, el área total del módulo se encuentra sombreada. Los valores insertados en esta matriz darán razón de la corriente de corto-circuito Isc de cada módulo, como se expresa en (10).
Isc = Iph *mismatch(NxM) (10)
Los 5 parámetros por módulo se almacenan en una matriz Mpar como la descrita en (11) correspondiente al tamaño del arreglo, de esta manera se permite efectuar simulaciones de fallas por degradación al in- gresar variaciones de δRs y δRsh realizando una simple suma matricial a las variables Rs y Rsh encontradas por el algoritmo como se ilustra en (12) con el elemento (2,1) como ejemplo.
Por último, mediante un análisis circuital del arreglo PV se obtienen la corriente y el voltaje para determinar al perfil de potencia con las condiciones ambientales descritas al inicio del proceso y con la manipulación de estas variables puede llevarse a cabo un análisis de degradación.
3. Resultados y Discusión
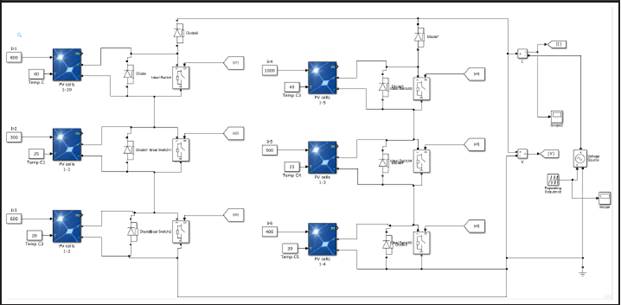
Con el objetivo de validar el análisis propuesto, se plantea un sistema de simulación compuesto por diferentes módulos PV conectados en serie y en paralelo con el fin de construir un arreglo fotovoltaico. Los módulos seleccionados para el entorno de simulación corresponden a la referencia Jinko Solar JKM230P-60 con un voltaje de circuito abierto Voc = 36.8 V, corriente de corto-circuito Isc = 8.35 A, Máxima potencia Pmáx = 230.28 W, voltaje en el punto de máxima potencia Vmpp = 29.6 V y una corriente en el punto de máxima potencia Impp = 7. 78 A. Con el fin de validar el modelo matemático propuesto como herramienta para analizar arreglos PV con respecto a sistemas de simulación para sistemas PV, se propone un sistema inicial de configuración 3x2 (2 cadenas compuestas de 3 módulos en serie cada una) simulado en la interfaz Simulink de Matlab como lo presenta la Figura 4 .
Dicho sistema se simulo y comparo con respecto al modelo matemático presentado en la sección anterior bajo las mismas condiciones de operación. La Figura 5 presenta las curvas P-V obtenidas tanto del modelo como de Simulink, con diferentes condiciones de sombreado parcial, particularmente, bajo 3 escenarios de simulación: Todos los módulos PV con una irradiación homogénea de 1000 W/m2, las primeras dos filas con una irradiación de 1000 W/m2 y la última fila con 500 W/m2; y como última prueba, la primera fila con una irradiación de 1000 W/m2, la segunda con 500 W/m2 y la tercera con 300 W/m2. Para cada escenario de simulación se presenta el perfil obtenido mediante la herramienta Simulink en contraste con el modelo matemático.
Como se puede evidenciar en la Figura 5, el modelo matemático replica correctamente el comportamiento de un arreglo fotovoltaico sometido a diferentes niveles de irradiación. El error obtenido entre el modelo de Simulink y la implementación del modelo para fallas propuesta es bajo, aplicando un índice de error MAPE descrito en (13) en el GMPP se encuentra que este error corresponde al 0.6134 % para la curva que no presenta sombreado parcial, 1.0203 % para la curva que presenta sombreado parcial para la última fila del arreglo y 0.3982 % para la curva que presenta sombreado parcial en la segunda y tercera fila del arreglo PV, por lo cual se considera que la predicción realizada por el algoritmo matemático imple- mentado para la emulación del sistema PV es adecuado y puede ser utilizado para el análisis de los impactos de las perdidas por degradación de módulos en arreglos PV.
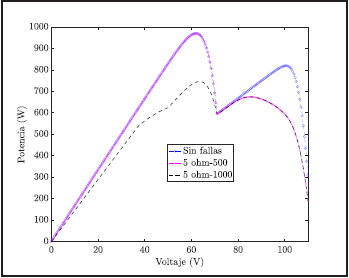
Seguidamente, con el fin de validar la efectividad del diagnóstico de fallas mediante el modelo matemático se procede a simular el sistema 3x2 con incrementos en las resistencias de los diferentes módulos PV. Los resultados del modelo se presentan en el perfil de la Figura 6, donde la línea azul representa la característica potencia- voltaje del sistema sin fallas con una irradiación de 1000 W/m2 en las dos primeras filas y 500 W/m2 en la fila 3, como se ilustro en la Figura 5.
Así mismo, se ejecutó el modelo matemático con un incremento de 5 Ω en los módulos con una irradia ción de 500 W/m2 evidenciado en el perfil de color rosa, en el cual se puede notar que hay un decremento de la potencia para los niveles de voltaje superiores a 80 V.
Finalmente, se calculó el perfil del arreglo PV con un incremento en la resistencia de 5 Ω en los paneles con irradiación de 1000 W/m2, el cual se ilustra en la Figura 6 con color negro. Dicho perfil, evidencia un decremento considerable en la generación de potencia para voltajes del rango de 60V, donde incluso el GMPP se ve afectado en consideración, como se detalló en la sección anterior.
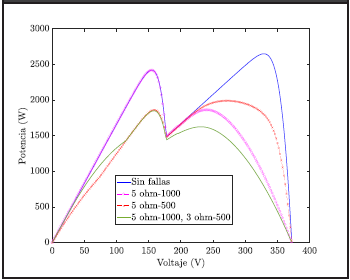
Tomando como fortaleza la capacidad del modelo matemático para simular arreglos PV de gran magnitud sin la necesidad de implementar sistemas de emulación basados en conexiones eléctricas como las que se requieren en Simulink, se procede a simular dos sistemas PV de mayores proporciones. Se implementaron mediante el modelo matemático un arreglo 10x2 (2 Cadenas compuestas de 10 módulos en serie cada una) y un sistema 20x5 (5 Cadenas compuestas de 20 módulos en serie cada una); presentados en las Figuras 7 y 8, respectivamente.
Así mismo, se ejecutó el modelo matemático con un incremento de 5 Ω en los módulos con una irradiación de 500 W/m2 evidenciado en el perfil de color rosa, en el cual se puede notar que hay un decremento de la potencia para los niveles de voltaje superiores a 80 V. Inicialmente se implementó un sistema de 10x2 módulos PV bajo los mismos escenarios de irradiación descritos en el sistema 3x2, donde, el perfil de color azul representa el sistema con una irradiación de 1000 W/m2 para las primeras 5 filas de módulos y de 500 W/m2 para las siguientes 5 filas de módulos, como se presenta en la Figura 7. Así mismo, se llevó a cargo una simulación del sistema con un incremento de la resistencia en 5 Ω para los módulos de 1000 W/m2 descrito por el color rosa, luego la perdida con el mismo valor de resistencia fue asignado a los módulos con irradiación de 500 W/m2, evidenciado con color rojo. Finalmente se llevó a cabo una prueba de combinación de niveles de degradación asignando una pérdida de 5 Ω en los módulos de 1000 W/ m2 y 3 Ω en los módulos de 500 W/m2, el cual se presenta con perfil verde. Dicho sistema evidencia las diferencias que existen entre los perfiles con degradación antes las mismas condiciones sombreado parcial, donde los GMPP cambian en función de las características del arreglo, lo que dificulta su estimación previa para el diagnóstico de la generación de energía del sistema.
Finalmente, se presenta la implantación del sistema 20x5 (100 módulos) en la Figura 8, donde las condiciones de irradiación se establecen como 1000 W/m2 para las primeras 10 filas y 500 W/m2 para las siguientes 10 filas de módulos. El perfil calculado por el modelo matemático para un sistema sin degradación es presentado en color magenta, donde el GMPP se ubica alrededor de los 660 V.
Del mismo modo, se implementa una pérdida de 5 Ω en los 50 módulos con irradiación de 1000 W/m2, ilustrado con color naranja el cual posee un GMPP en 480 V y el LMPP prácticamente desaparece por el efecto de la degradación. Por otro lado, se implementa solo una pérdida de 5 Ω en los 50 módulos con 500 W/m2, ilustrado con color negro donde el GMPP se ubica en 310 V, cambiando así las condiciones de operación con respecto al sistema sin fallas. Como última prueba, se implementó un modelamiento matemático del sistema con una pérdida de 5 Ω en los módulos de 1000 W/m2 y 3 Ω en los módulos de 500 W/m2, el cual se presenta con perfil violeta. Esta simulación ilustra el efecto significativo que poseen las perdidas por degradación en arreglos fotovoltaicos al modificar los perfiles típicos que se pueden encontrarse en sistemas sin degradación o bajo condiciones de simulación ideal, lo que implica que deben ser analizados al detalle para su posterior corrección.
Las simulaciones realizadas permiten concluir que el FF no es un buen parámetro para medir la degradación cuando se presentan condiciones de sombreado parcial, ya que puede afectarse el LMPP y no el GMPP que es el que se tiene en cuenta en el cálculo de dicho factor. De igual forma, en los resultados de las simulaciones se puede observar que la degradación tiene menos impacto si el panel tiene un nivel de radiación menor que el de los demás paneles del arreglo. La motivación principal de este estudio fue la poca información encontrada en la literatura relacioada con herramientas o procedimientos para cuantificar o indicar la degradación en arreglos que operan bajo condiciones de sombreado parcial. Como trabajo futuro derivado de este primer estudio, se propone estudiar el efecto de diferentes configuraciones (Total Cross Tied - TCT, Bridge-Linked - BL, Honey-Comb - HC, entre otras) en la mitigación de los efectos de la degradación en arreglos que operen bajos condiciones de sombreado parcial ya que en este artículo se trabajó únicamente con arreglos en configuración Series Parallel - SP; en este análisis puede ser muy útil el procedimiento presentado en (Bastidas-Rodriguez, et al., 2018) ya que mediante dicha herramienta es posible obtener las curvas P-V de cualquier arreglo conectado en cualquier configuración. De igual forma, se propone introducir nuevas expresiones matemáticas que involucren la potencia de los LMPP en el cálculo de un nuevo indicador (similar al FF) que permita tener en cuenta la relación entre la degradación y el nivel de radiación de cada panel en un arreglo PV. Finalmente, otro problema de investigación que queda abierto es la proposición de técnicas para detectar la posición del panel degradado dentro del arreglo, ya que el sólo análisis de la forma de la curva y de los cambios en los puntos de máxima potencia no indican con certeza cuál parte del arreglo está siendo afectada por la degradación