Por qual motivo estudantes apresentam dificul dades em matemática? Os dados são consistentes sobre a existência de déficits no aprendizado dessa disciplina. Em relação ao ensino funda mental brasileiro, resultados do PISA (Programme for International Student Assessment) de 2018 mostraram que o Brasil ficou abaixo da média mundial (492), obtendo apenas 384 pontos em matemática (Brasil, 2019a). Nas provas do SAEB (Sistema de Avaliação da Educação Básica) de 2017, constatou-se que o aprendizado em matemática está no limite inferior do nível básico, Nível 4 de 10 (Brasil, 2019b). Além disso, estudos revelam que apesar da importância da matemática para a vida das pessoas, muitos estudantes identificam essa disciplina como difícil e geradora de ansie dade (Mendes, 2016). No senso comum, é usual ouvir que a dificuldade com a matemática reside na falta de "base" ou que o estudante apresenta desempenho ruim porque não sabe a "base". Mas, a que esse termo se refere?
Um exame analítico-comportamental pode auxiliar a esclarecer o que significa ter "base" em matemática. Esse termo se refere a comporta mentos necessários ou que são componentes do comportamento que precisa ser aprendido (Neef et al., 2003; Cortegoso & Coser, 2013). Ainda hoje, uma das principais lacunas na área educacional consiste no baixo grau de clareza sobre o que é necessário aprender para viabilizar a aquisição de cada comportamento que os educadores definem como objetivo de ensino (Kubo & Botomé, 2001), incluindo o caso dos comportamentos matemáticos. Por essa razão, pesquisadores têm se dedicado a investigar quais são os comportamentos que cons tituem a base para a aquisição de comportamentos como conceituar números, somar, subtrair, resolver problemas com funções de primeiro grau ou fra ções, manejar dinheiro entre outros (e.g., Haydu et al., 2019).
Um exemplo a esse respeito pode ser útil para esclarecer a noção de que alguns comportamentos devem ser aprendidos para que outros possam ser desenvolvidos. Se uma criança, quando solicitada a contar quantos elementos um conjunto possui, co mete um erro, tem-se um indício, descartadas outras hipóteses (e.g., transtornos de aprendizagem), de que um ou mais comportamentos necessários para "contar", não foram adquiridos. Mas, quais seriam esses comportamentos? Poderia ser avaliado se a criança consegue recitar adequadamente os nomes dos números na ordem crescente, se consegue, ao contar, relacionar cada número recitado com apenas um elemento do conjunto a ser contado, se sabe identificar que o último número recitado corresponde ao total de elementos do conjunto e assim por diante.
Cortegoso e Coser (2013) denominam de decom posição a esse processo de descrição dos comporta mentos mais básicos e constituintes ou necessários para outro comportamento mais abrangente. Parte-se de um verbo mais geral, que designa o comportamento-objetivo a ser ensinado, que neste caso seria contar, e por meio de perguntas como "o que é preciso ser capaz de fazer para...?" são identifi cadas classes de comportamentos mais específicas, tais como recitar nomes dos números. Diante desses elementos teóricos, surge a questão sobre quais são os comportamentos matemáticos em relação aos quais estudantes brasileiros têm apresentado maior dificuldade e quais são os comportamentos mais específicos que os constituem?
Os dados apresentados do PISA e do SAEB in dicam que os alunos brasileiros não conseguem resolver problemas aritméticos elementares. Historicamente, o ensino desse repertório tem represen tado um desafio para os educadores matemáticos (Haydu et al., 2010). Fica evidente, portanto, a necessidade de decomposição do comportamento de resolver problemas aritméticos como condição para que a avaliação e o ensino sejam mais eficazes.
Considerando essa necessidade, o estudo de Resnick et al. (1973) é considerado clássico justamente por ter sido um dos primeiros a examinar sistemati camente os componentes comportamentais de clas ses mais gerais de comportamento como "somar" e "subtrair", que são classes constituintes importantes do comportamento de resolver problemas aritméti cos. Os autores identificaram, por exemplo, que o comportamento de somar mais básico, envolve unir dois conjuntos e contar o total de elementos, e que o comportamento de subtrair implica em retirar um conjunto menor de um conjunto maior e contar os elementos remanescentes do conjunto maior. Para exibir esses comportamentos era preciso que o aprendiz tivesse adquirido um repertório prévio, tais como comportamento conceitual numérico, contar, comparar conjuntos, ordenar valores, etc. A análise dos pesquisadores foi ainda mais especí fica, pois envolveu comportamentos básicos como "diante de três objetos identificar maior e menor", "ordenar objetos de acordo com o tamanho", "re citar numerais em ordem crescente", "diante de um numeral, selecionar a representação correspondente do numeral", entre outros.
Existem contribuições na literatura analítico-comportamental posteriores ao trabalho de Resnick et al. (1973) que ajudam a identificar os componen tes da soma e da subtração. O estudo conduzido por Donini (2005), por exemplo, representa um avan ço no exame dos comportamentos de somar e de subtrair, pois a autora considerou diversas fontes de informação para construir um instrumento que permitisse avaliar esse repertório. Ela analisou o Referencial Curricular Nacional para a Educação Infantil (1998), os Parâmetros Curriculares Na cionais para o Ensino Fundamental (2000), livros didáticos e programas de ensino desenvolvidos por analistas do comportamento. Ao final do seu tra balho, a autora identificou cerca de 124 classes de comportamento que deveriam ser garantidas para que o aprendiz fosse capaz de somar e subtrair. Essas classes envolvem comportamentos descri tos por Resnick et al. (1973), e outros descobertos como "identificar, em uma sequência de numerais, o numeral correspondente a um número ditado", "localizar, em uma sequência de numerais, os nu merais que estão ausentes em uma outra sequência de numerais" e "recitar os números de um a nove em sequência decrescente, sem quaisquer dicas fornecidas por outra pessoa".
Outro estudo importante para o ensino de arit mética, incluindo desta vez pessoas com deficiên cia, foi conduzido por Araújo e Ferreira (2008). Eles trouxeram a inovação de tentar descrever o comportamento de subtrair como uma rede de rela ções equivalentes. Araújo e Ferreira (2008) testaram o efeito do ensino de um conjunto de relações entre estímulos sobre o desempenho de três pessoas com transtorno do desenvolvimento intelectual. Foram ensinadas as relações entre "numeral falado" (A, e.g., "dois") e "conjunto" (B, e.g., "**"), "numeral falado" (A) e "algarismo impresso" (C, e.g., "2") e, então, foi testada a formação da classe ABC, bem como o comportamento de nomear os estímulos das classes B e C. Na sequência foram ensinadas e testadas relações envolvendo os seguintes estímu los: "operador falado" (e.g., "menos"), "operador impresso" (e.g., "-"), "palavra impressa" (e.g., "MENOS"), "sentença falada" (e.g., "dois menos um é igual a"), "sentença com conjuntos" ("** - * ="), "sentença com algarismos" (e.g., "2-1="). Os re sultados encontrados mostraram melhora clara de um dos participantes e ganhos de repertório para os outros dois, o que revela a possibilidade de se ensinar matemática para pessoas com transtorno do desenvolvimento intelectual. Basta, para isso, clareza sobre o que deve ser ensinado, conhecimen to do repertório do aprendiz e arranjo adequado de contingências.
Apesar do avanço promovido pelos três estudos descritos, ainda não se pode afirmar que todos os componentes do repertório de somar e subtrair estejam claros. Um dos motivos é que os estudos empíricos analítico-comportamentais, que adotam tais descrições como objetivos de ensino, são es cassos (Henklain et al., 2017). Esses estudos são necessários porque é o sucesso do ensino que per mite inferir que a descrição comportamental seja adequada. Além disso, estudos conduzidos desde a década de 80 (e.g., Hiebert, 1982; Carpenter et al., 1988) revelam outros comportamentos que não foram identificados nas pesquisas supracitadas, indicando, portanto, a necessidade de complementação do que foi descrito. Portanto, ainda não existe uma descrição consensual dos comportamentos de somar e subtrair suficiente para garantir um ensino eficaz a pessoas com diferentes repertórios e necessidades, o que impacta negativamente so bre o aprendizado do comportamento de resolver problemas aritméticos. Por esse motivo é preciso continuar investigando.
Os comportamentos descobertos a partir da década de 80 estão relacionados com as habilida des de discriminar como resolver problemas em diferentes formatos de apresentação, discriminar como resolvê-los quando a posição da incógnita varia e, ainda, discriminar como resolver problemas quando ele é apresentado no formato de sentença em diferentes estruturas semânticas (e.g., transfor mação e comparação). Esse repertório começou a ser investigado por analistas do comportamento a partir do paradigma de equivalência de estímulos. Os resultados encontrados indicam que são comportamentos que, quando aprendidos, melhoram o desempenho da pessoa na resolução de problemas. Os estudos a seguir mostram evidências disso.
Haydu et al. (2006) investigaram o efeito do ensino de classes de equivalência com três formas de apresentação de problemas de adição sobre o comportamento de resolver problemas aritméticos. Participaram sete alunos da primeira série do En sino Fundamental, que realizaram um pré-teste e, após a intervenção, um pós-teste com problemas de adição impressos nas formas de balança, operação e sentença linguística. A maioria dos participantes apresentou aumento, superior a 20 %, nas por centagens médias de acerto entre as situações de pré e pós-teste.
A partir do sucesso obtido por Haydu et al. (2006), Henklain e Carmo (2013a) decidiram in vestigar se a formação de classes de equivalência entre quatro tipos de apresentação de problemas de adição aumentava a porcentagem de acertos em problemas (de adição e subtração) com diferentes formas de apresentação, posições da incógnita e estruturas semânticas de problemas escritos. Parti ciparam oito estudantes do 2° ao 5° ano do Ensino Fundamental. Foram aplicados um pré-teste e um pós-teste. A porcentagem média geral dos partici pantes no pré-teste foi de 54 % de acertos. Após a intervenção, a porcentagem média no pós-teste foi de 75 %, indicando aumento de 21 %. Os dados obtidos corroboraram os de Haydu et al. (2006), in clusive, em termos de ganhos com o procedimento.
Henklain e Carmo (2013b) decidiram, então, avaliar se a formação de dois conjuntos de clas ses equivalentes de adição e subtração promove ria aumento de acertos na resolução de problemas aritméticos de adição e de subtração. Participaram oito estudantes do 2° ao 5° ano do Ensino Fundamental. No pré-teste, a média do resultado dos participantes foi de 41.5 %. Os resultados mos traram que após a formação das classes, todos os participantes apresentaram crescimento médio de 25 % no pós-teste.
Foi, então, levantada a questão sobre se es se procedimento poderia também melhorar o de sempenho de adultos na resolução de problemas aritméticos. Haydu et al. (2015) coletaram dados com quatro mulheres, em fase de alfabetização, com idades entre 37 e 71 anos. Após os treinos, todas as participantes apresentaram melhora nos resultados do pós-teste (média de 98.8 %) em comparação ao pré-teste (média por volta de 50 %).
De acordo com Haydu et al. (2006), o que é endossado por Henklain e Carmo (2013a, 2013b), a formação de classes de equivalência entre diferentes formas de apresentação de problemas favorece a melhora no desempenho por, pelo menos, dois motivos: (a) a pessoa aprende a usar estratégias de solução de problemas que aplica para as formas com as quais possui facilidade em relação àquelas com as quais possui dificuldade; (b) a pessoa aprende a ficar sob controle dos aspectos de um problema necessários para resolvê-lo, independente do formato, isto é, os valores envolvidos, como estão relacionados e a operação que deve ser executada.
Com base nos resultados promissores descritos, nota-se que a formação de classes de equivalência entre diferentes formas de apresentação de problemas, posições de incógnita e estruturas semânticas de problemas escritos compõe o repertório a ser aprendido sobre resolução de problemas e, por ser de fácil ensino, tem potencial para que seja aperfeiçoado e utilizado por professores de ma temática. Antes que isso ocorra, porém, é preciso ampliar a diversidade das amostras que foram expostas a esses procedimentos e a qualidade do delineamento empregado. Nos estudos anteriores, os participantes foram, predominantemente, crian ças das Regiões Sul e Sudeste realizando tarefas em um delineamento A-B no qual o grau de con fiança de que a mudança comportamental se deu em função do procedimento é menor. Também não foram consideradas as práticas de estudo dos par ticipantes, a presença de ansiedade à matemática e a aplicação de testes padronizados relacionados a habilidades de leitura e escrita ou matemática como formas de controlar variáveis intervenien tes em relação ao desempenho dos participantes.
Considerando as lacunas existentes na literatura, esta pesquisa foi conduzida com amostras de crian ças da Região Norte do Brasil. O objetivo geral foi investigar o efeito da formação de classes de equi valência entre diferentes formas de apresentação de problemas, envolvendo diferentes posições da incógnita e estruturas semânticas dos problemas escritos sobre o desempenho na resolução de pro blemas de adição e de subtração. O delineamento adotado foi o de linha de base múltipla. Além disso, foram aplicados instrumentos para avaliar hábitos de estudo, nível de ansiedade à matemática e o repertório de leitura e escrita.
Método
Visão geral
Foi adotado o delineamento de linha de base múltipla (LBM) entre participantes, composto pelas seguintes fases: (a) medida da VD na linha de base (pré-teste) para todos os participantes; (b) inser ção da VI para um participante, X, e aplicação do pré-teste para os demais, Y e Z; (c) medida da VD (pós-teste) para X e aplicação do pré-teste para Y e Z; (d) inserção da VI para Y, aplicação do pós-teste para X e do pré-teste para Z; (e) aplicação do pós--teste para X e Y e aplicação do pré-teste para Z; (f) inserção da VI para Z e aplicação do pós-teste para X e Y; (g) aplicação do pós-teste para todos. A VD foi a resposta-solução aos problemas aritmé ticos. A VI foi o ensino de uma dentre duas classes de equivalência possíveis (adição ou subtração).
Participantes
Participaram do estudo seis alunos que cursa vam o 4° e 5° ano do Ensino Fundamental de uma escola pública, com idades entre 10 e 13 anos, que obtiveram mais de 70 % de acerto no Teste de Desempenho Escolar (TDE) na prova de leitura e, pelo menos, mais de 60 % na prova de escrita, que já haviam aprendido na escola a somar e subtrair e com porcentagem de acertos na primeira aplicação do pré-teste inferior ou igual a 65 %. Os participantes P1, P2 e P3 foram designados para o procedimen to de adição e P4, P5 e P6 para o de subtração. A tabela 1 exibe os dados dos participantes e resultados de medidas que foram realizadas para avaliar seu repertório de entrada, práticas de estudo de matemá tica e presença ou não de ansiedade à matemática.
Verifica-se na tabela 1 que, no subteste de arit mética do TDE, P2, P3, P4 e P5 obtiveram classi ficação inferior. Apenas P1 obteve desempenho médio. Em relação à escrita e leitura, embora P1 e P3 tenham ficado na classificação inferior, segundo grupo normativo do TDE, todos atingiram os crité rios definidos para este estudo. Em relação à Escala de Ansiedade à Matemática (EAM), os participantes demonstraram ter baixa ou moderada ansiedade. Portanto, desempenhos ruins em matemática não devem estar associados com uma função aversiva dos estímulos matemáticos. Quanto aos hábitos de estudo, a média dos resultados foi de 1,6. Logo, os hábitos de estudo, a exceção de P2, não parecem ser uma variável, nessa amostra, que justifique eventuais dificuldades em matemática.
Tabela 1 Resultado dos testes preliminares
| p | sx | iD | AES | EAM | IHEM - | TDE Aritmética | TDE Ditado | TDE Leitura | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PB | % | CL | PB | % | CL | PB | % | CL | ||||||
| 1 | M | 10 | 4° | 3.36 | 1.47 | 15 | 39.47 | MD | 23 | 65.71 | IF | 59 | 84.29 | IF |
| 2 | F | 10 | 4° | 2.96 | 0.94 | 13 | 34.21 | IF | 28 | 80.00 | MD | 67 | 95.71 | MD |
| 3 | F | 10 | 5° | 2.92 | 2.00 | 16 | 42.11 | IF | 22 | 62.86 | IF | 64 | 91.43 | IF |
| 4 | F | 13 | 5° | * | 2.03 | 14 | 36.84 | IF | 30 | 85.71 | MD | 67 | 95.71 | MD |
| 5 | M | 11 | 5° | 3.75 | 1.5 | 17 | 44.74 | IF | 29 | 82.86 | MD | 69 | 98.57 | SP |
| 6 | M | 10 | 5° | 1.96 | 1.79 | 19 | 50.00 | MD | 39 | 88.23 | MD | 69 | 98.57 | SP |
Nota: P = participantes; sx = sexo; ID = idade; AES = Ano do Ensino Fundamental; * = p4 marcou aleatoriamente a EAM, por isso os seus resultados não foram considerados; PB = pontos brutos; % = porcentagem; CL = classificação baseada percentil conforme manual do teste; MD = médio; IF = inferior; SP = superior.
Local e Materiais
As coletas foram realizadas na brinquedoteca ou na sala de música da escola na qual os participantes estudavam. As sessões foram desenvolvidas no computador, em um programa criado no Excel 2010 com o Visual Basic for Applications (VBA), que permitia realizar o procedimento de MTS (Matching to Sample ou, em português, Escolha de Acordo com o Modelo). A criança se sentava diante de uma mesa que continha um notebook de 14 polegadas. Durante a aplicação dos testes, havia sobre a mesa apenas o caderno de questões, lápis, borracha e o teste a ser respondido.
Instrumentos
Teste de Desempenho Escolar I (TDE): instru mento de aplicação individual que avalia três áreas específicas: leitura (reconhecimento de palavras isoladas do contexto) com 70 itens, escrita (escrita do nome próprio e de palavras contextualizadas, apresentadas sob a forma de ditado) com 35 itens e aritmética (solução oral de problemas e cálculo de operações aritméticas por escrito) com 38 itens. Foi desenvolvido para 1a a 6a séries do Ensino Fundamental. O Alpha da escala total foi de 0.95 (Stein, 1994).
Escala de Ansiedade à Matemática (EAM): ava lia o nível de ansiedade à matemática por meio de escala Likert, que varia de "1 = Nenhuma ansiedade" a "5 = Extrema ansiedade". A es cala contém 25 itens. O Alpha da EAM foi 0.90 (Mendes, 2016) e nesta amostra 0.92.
Inventário de Hábitos de Estudo de Matemática (IHEM, medida em construção disponibilizada pa ra pesquisa pelo autor, Prof. Dr. João dos Santos Carmo): avalia práticas de estudos. Possui 34 itens, no qual os escores variam de zero a três, e um questionário complementar com sete itens. O Alpha nesta amostra foi de 0.63.
Teste de Matemática (usado como pré e pós-tes te): avalia desempenho na solução de problemas de adição ou subtração. Possui 24 itens, dividi dos nos três tipos de apresentações de problemas: 12 itens escritos (6 itens na estrutura semânti ca de transformação e 6 itens na estrutura de comparação); 6 itens na forma de algarismos e 6 itens na forma de conjunto (representados com círculos e triângulos). Para cada forma de apresentação, a incógnita poderia estar em a, b ou c (e.g., ?+b=c, a+?=c e a+b=?). Foram utilizadas nas diferentes formas as seguintes operações: ?+5=9; 2+?=8; 2+4=?; ?+13=28; 19+?=30; 13+10=?; ?+3=8; 2+?=9; 2+8=?; ?+16=27; 20+?=30; 11+10=?; ?+3=10; 3+?=8; 4+3=?; ?+14=26; 11+?=24; 10+15=?; ?+6=10; 6+?=9; 2+5=?; ?+12=22; 11+?=25; 12+17=?; ?-4=5; 8-?=5; 6-2=?; ?-11=14; 27-?=15; 29-18=?; ?-5=2; 5-?=3; 10-6=?; ?-12=16; 27-?=13; 25-15=?; ?-3=6; 7-?=5; 8-5=?; ?-11=15; 25-?=12; 29-16=?; ?-2=7; 8-?=6; 6-4=?; ?-10=20; 29-?=17; 27-16=?.
Estímulos
Os participantes foram expostos a três tipos de apresentação de problemas: (a) problemas na forma de algarismos; (b) problemas escritos, com uma de duas estruturas semânticas, transforma ção (quando um valor inicial é modificado por acréscimo ou retirada) e comparação (quando é realizada uma comparação entre dois valores); (c) problemas na forma de conjuntos. Os problemas poderiam ter uma de três posições de incógnita: a, b e c. Optou-se por trabalhar apenas com números inteiros com até dois dígitos e com resultado má ximo igual a trinta, sendo que os problemas com números de dois dígitos mais difíceis ficaram nos testes. A figura 1 exibe todos os estímulos usados nas sessões para a formação das classes de equi valência de adição e de subtração.
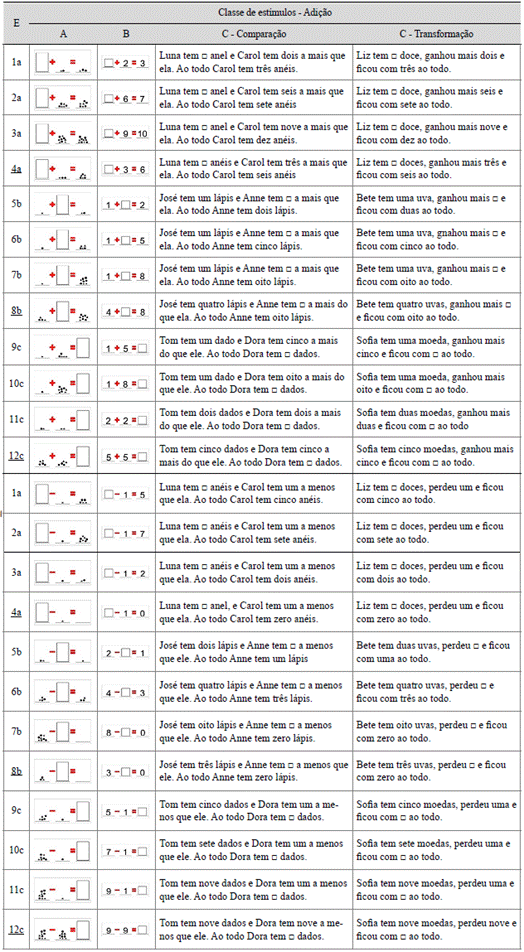
Nota: E = estímulo; Letras ao lado dos números = posição da incógnita; números sublinhados = sonda.
Figura 1 Estímulos utilizados nas sessões de treino e teste das relações de equivalência
Nas sessões de treino e teste no computador, o estímulo-modelo ficava na parte superior da tela e três estímulos-comparação eram apresentados na parte inferior. Nas tentativas de treino, a consequência para acertos era o som "Muito bem!" e para erro "Não, não é!". Nas tentativas de teste, não havia feedback sobre acerto ou erro.
Procedimento de coleta de dados
A direção da escola foi consultada e, mediante autorização, as pesquisadoras visitaram as salas de aula para explicar os objetivos do estudo e pergun tar quais crianças gostariam de participar. Aquelas que manifestaram interesse levaram o Termo de Consentimento Livre e Esclarecido (TOLE) para que os pais ou responsáveis assinassem. As crianças levaram também o Termo de Assentimento Livre e Esclarecido (TALE), que precisava ser assinado pela criança. As coletas foram realizadas em ho rário oposto ao das aulas.
As crianças autorizadas a participar, após assi natura dos termos, foram conduzidas a um auditório onde foi aplicado o pré-teste. Aquelas que obtive ram porcentagem de acertos menor ou igual a 60 % foram selecionadas para continuar no estudo. Em seguida, o TDE foi aplicado individualmente. Para cada subteste, a pesquisadora orientava como a criança deveria proceder. Não havia limite de tempo e era informado que a criança só precisava respon der aquilo que já sabia. Após isso, foram aplicadas em grupo, no mesmo local, as escalas EAM e IHEM.
Terminada essa etapa, foi iniciado o delinea mento de LBM. O planejamento foi que todos os participantes deveriam realizar, pelo menos, três vezes o pré-teste para que se tentasse verificar estabilidade no desempenho. Depois disso, um participante de cada grupo iniciava o treino de discriminações condicionais, adição ou subtração, a depender do seu grupo, enquanto os demais con tinuavam respondendo ao pré-teste. Quando um participante finalizava a intervenção, ele passava a responder ao pós-teste, enquanto o participante subsequente começava a intervenção e o último permanecia respondendo ao pré-teste. Somente quando o segundo participante finalizava a in tervenção, e iniciava o pós-teste, é que o terceiro começava o treino. A figura 2 exibe as relações ensinadas e testadas.

Nota: S = estímulo; tts = número de tentativas.
Figura 2 Relações ensinadas e testadas relativas à classe de adição (parte esquerda da figura) e à classe de subtração (parte direita da figura)
Nas tentativas de MTS foi usado o modelo de MTS simultâneo. Antes de iniciar o bloco, a pesquisadora apontava para o estímulo na tela do computador e dizia: "você está vendo este estímulo aqui em ci ma? Você terá de encontrar entre esses abaixo qual é igual ao de cima. Só um desses abaixo é igual ao de cima". Caso o participante acertasse menos que 75 % das relações ensinadas, ele tinha que re petir o bloco. Eram permitidas até três repetições. Se esse critério não fosse atingido, o participante era excluído do experimento. Conforme pode ser observado na figura 2, os blocos das relações AB e BA eram compostos por 12 estímulos, e cada estímulo podia ser repetido até três vezes, resultando em um total de 36 tentativas. No terceiro erro, o programa seguia em frente. Enquanto os blocos das relações AO, CA, BC e CB, que continham dois tipos de sentença (C), eram compostos cada um por 24 estímulos, e cada estímulo podia ser repetido até três vezes, resultando em um total de 72 tentativas. A consequência das tentativas era um som emitido pelo computador. Por exemplo, quando o participan te acertava, ouvia: "Muito bem!". Quando errava, ouvia: "Não, não é". Entre as tentativas aparecia uma tela preta com um botão que o participante deveria pressionar para seguir adiante.
Além dos treinos, também eram feitos testes, durante os quais não havia feedback de acerto ou erro. Nos testes, eram avaliadas as relações emergentes. Foram testadas as relações de simetria, transitividade e simetria da transitividade. O crité rio de aprovação nos testes era de, no mínimo, 70 % de acertos, sendo permitidas até três repetições do bloco. Caso esse critério não fosse atingido, a crian ça era excluída do experimento. Antes dos testes começarem, a pesquisadora dizia ao participante: "agora, você vai escolher qual é igual ao de cima, mas o computador não vai te dizer se está correto ou não. Por isso, você precisa dar o seu melhor". Foi planejado que as crianças responderiam três blocos de MTS por dia. Porém, devido a faltas e a proximidade de encerramento do período letivo, foram realizados mais de três blocos diários com algumas crianças, mediante a sua concordância para que a tarefa não ficasse cansativa.
Procedimento de análise de dados
Foram calculadas as porcentagens de acerto em cada fase de ensino, bem como no pré e no pós-teste. Os instrumentos selecionados foram corrigidos e interpretados conforme as informa ções do manual ou de artigo, que descrevia o modo adequado de correção e interpretação.
Resultados
Verificou-se nesta amostra que foi difícil con duzir o experimento até o final, pois as crianças reclamavam da duração das sessões de treino e, principalmente, de precisarem repetir várias ve zes os testes de matemática. Próximo do final da pesquisa, P6 possivelmente desistiu por essa ra zão. Assim, na amostra final, permaneceram P1, P2 e P3 do grupo de adição, e P4 e P5 do grupo de subtração. A figura 3 exibe o desempenho dos participantes nas sessões para formação das classes de equivalência.
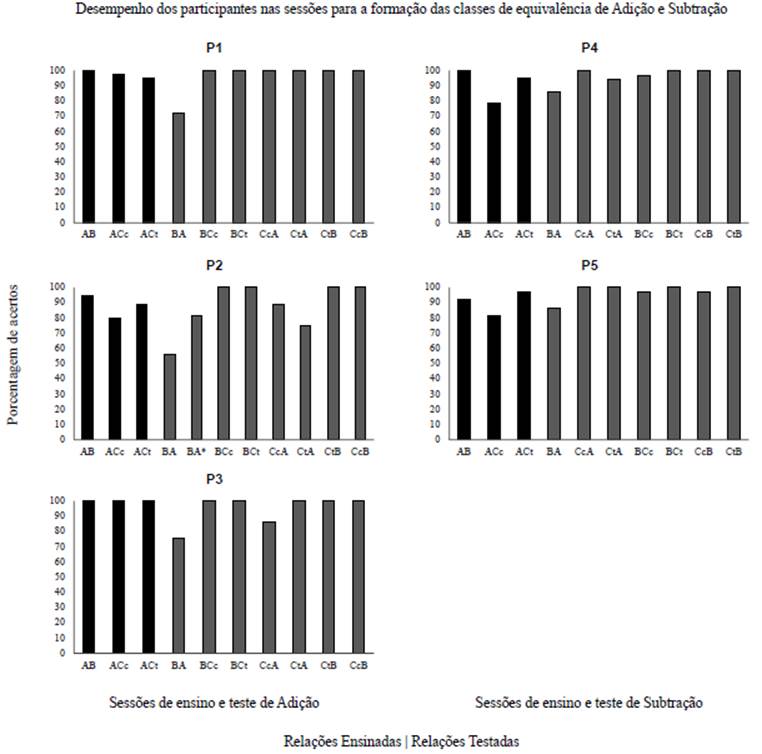
Nota: c = problema no formato de sentença com estrutura semântica de comparação; t = problema no formato de sentença com estrutura semântica de transformação; * = bloco repetido.
Figura 3 Relações ensinadas e testadas no treino mts de adição e subtração
Nota-se na figura 3 que P3 apresentou 100 % de acertos nos blocos de treino, P1 obteve desem penho acima de 90 % e os outros três participantes tiveram desempenho satisfatório acima de 75 %. Nos testes de equivalência, P1 obteve desempenho satisfatório no teste BA e atingiu 100 % de acertos nos demais. P4 e P5 apresentaram desempenho próximo a 100 % em quase todos os testes, e P3 teve um desempenho similar, tendo apresentado menor porcentagem de acertos no teste BA. P2, por fim, apresentou desempenho satisfatório, com 100 % de acertos em quatro testes, mas precisou repetir um bloco, no teste BA, que foi a sessão na qual os participantes de adição pontuaram menos.
A figura 4, por sua vez, exibe a porcentagem de acertos de cada participante ao longo das apli cações do teste com problemas de matemática. Os testes que foram realizados antes da intervenção foram chamados de pré-teste, e aqueles realizados após foram denominados de pós-teste. A figura 4 exibe os resultados dos participantes expostos ao procedimento de adição (P1, P2 e P3, na por ção esquerda da figura) e ao procedimento de subtração (P4 e P5, na porção direita da figura).

Nota: As linhas verticais tracejadas indicam o momento de realização do treino para formação das classes de equivalência e, portanto, de marcam a separação dos testes realizados antes (pré-teste) e após (pós-teste) a intervenção; a linha vermelha horizontal indica o maior valor de pré-teste obtido por cada participante, servindo ao propósito de facilitar a identificação de se houve ou não melhora de desempenho.
Figura 4 Desempenho nos pré-testes e pós-testes de P1, P2 e P3 (porção esquerda da figura), que formaram a classe de equivalência de adição, e de P4 e P5 (porção direita da figura), que formaram a classe de equivalência de subtração
Na figura 4, o traço horizontal de cor vermelha permite comparar se o desempenho no pós-teste foi superior ao que as crianças já haviam alcançado an tes da intervenção. Nota-se que P1 apresentou baixo desempenho no primeiro pré-teste e melhora de mais de 30 % no segundo pré-teste, tendo reduzido um pouco no último. Após a intervenção, P1 apresentou uma melhora de 20 % em relação ao pré-teste de maior pontuação, e uma diferença média entre pré e pós-teste de 29.17 %. Nos quatro pós-testes que realizou, o seu desempenho foi estável, variando entre, aproximadamente, 70 % a 80 % de acertos.
P2 faltou em duas sessões. Seu desempenho nos pré-testes ficou entre 25 % a 37.5 % de acertos. Embora estivesse com tendência de crescimento, por razões de cansaço das crianças, foi preciso iniciar a intervenção mesmo sem um critério cla ro de estabilidade. A diferença de desempenho entre o pré-teste de maior pontuação e o primeiro pós-teste foi de 45.83 %. Esse dado sugere que P2 se beneficiou da intervenção. Nos dois pós-testes seguintes, o seu desempenho caiu para 50 % e voltou a subir para 87.5 %. Em média, P2 teve um ganho de 32.29 %.
P3 também faltou em duas sessões, e seu de sempenho oscilou ao longo do experimento. No seu primeiro pré-teste ele apresentou 33.33 % de acertos, tendo obtido em um dos pré-testes 75 % de acertos. Em um dos pós-testes obteve 87.5 % de acerto, mas nos demais o desempenho foi igual ou inferior ao pré-teste de maior pontuação. Em média, P3 teve um ganho de 5.56 % com a intervenção. Considerando todos os ganhos, verificou-se que, em média, o aumento de desempenho no grupo de adição foi de 22.34 % (DP = 14.62).
P4 obteve pontuação de 33.33 % no primeiro pré-teste, sendo que deixou em branco 45.83 % da prova. Quando fez o segundo pré-teste, obteve 66.67 % de acertos, tendo alcançado no terceiro pré-teste 75 %. Não foi alcançada estabilidade de desempenho, mas, para evitar desistência, decidiu-se iniciar a intervenção. O resultado no primeiro pós-teste foi 75 %. Depois, P4 apresentou resultados superiores à maior pontuação do pré--teste durante todo o experimento. O seu ganho médio foi de 27.78 %.
P5, por fim, apresentou 45.83 % de acertos no primeiro pré-teste, mas deixou em branco 29.16 % da prova. Nos demais pré-testes apresentou desempenho elevado, tendo atingido pontuação de 87.50 %, com média, nos pré-testes, de 71.43 %. Após a intervenção, o seu desempenho foi igual ou inferior à sua pontuação máxima no pré-teste. A sua média nos dois pós-testes foi 83.34 %, sendo possível apontar que houve ganho de 11.90 % com a intervenção, embora mais medidas de pós-teste fossem necessárias. A média de ganho de P4 e P5, grupo de subtração, foi de 19.84 % (dp = 11.22).
Discussão
O objetivo deste estudo foi, por meio de um delineamento LBM entre participantes, investigar efeitos da formação de classes de equivalência entre problemas com diferentes formas de apresenta ção, envolvendo diferentes posições da incógnita e estruturas semânticas dos problemas escritos sobre a resolução de problemas de adição e sub tração. Foi observado que todos os participantes formaram as classes de equivalência planejadas. Ao examinar os resultados gerais, verificou-se um padrão semelhante ao de outros estudos da área, inclusive, com médias de ganhos entre pré-testes e pós-testes próximas a 20 %, tanto para o grupo de adição quanto de subtração (Haydu et al., 2006; Henklain & Carmo, 2013a,b). Esse dado sugere que o procedimento foi eficaz para melhorar o desempenho de crianças.
Apesar dos resultados positivos gerais, cumpre examinar também o desempenho dos participantes ao longo do experimento. A figura 4 evidenciou como o comportamento pode variar para um mesmo participante e entre participantes. Assim, com rela ção aos dados da literatura revisada, o delineamento de LBM mostrou de que forma a comparação entre um pré-teste e um pós-teste, no delineamento A-B, pode ser, eventualmente, enviesada. Verificou-se, por exemplo, que todos os participantes deste estudo apresentaram melhora de desempenho entre os pré-testes 1 e 2. Variáveis intervenientes podem ter interferido com o desempenho no pré-teste 1. Um exemplo disso foi o fato de que, nesse teste, as crianças estavam preocupadas com quanto tempo ele iria demorar, pois isso poderia afetar o horário do lanche - P4 e P5, inclusive, deixaram vários itens em branco. Nas sessões subsequentes, as crianças já conheciam o procedimento e sabiam que podiam ficar tranquilas.
Essas variáveis da familiaridade com o proce dimento e do efeito de atividades concorrentes po deriam explicar parte da diferença de desempenho nos pré-testes 1 e 2, sugerindo que o repertório das crianças era melhor do que de fato foi observado inicialmente. Outra variável que pode ter afetado o desempenho foram conversas entre os partici pantes sobre respostas corretas -uma estratégia para aprender como terminar a tarefa rapidamente e acertar mais. Essa variável também poderia ex plicar o aumento de desempenho no pré-teste 2.
Independentemente da variável que controlou o responder, se fosse um delineamento A-B, conclu sões favoráveis à intervenção poderiam, então, ser formuladas, mesmo que parte do ganho encontrado não fosse um produto dela. São por casos como esse que Sampaio et al. (2008) defendem que os dados produzidos em delineamentos de LBM são mais robustos.
Destaca-se, também, que o desempenho dos participantes foi afetado pela motivação com a tarefa, tendo sido difícil lidar com a perda de en gajamento à medida que precisavam repetir os testes. Foram observadas respostas ao longo da pesquisa com provável função de esquiva (e.g., faltas e atrasos) e de fuga (e.g., conversas na hora da aplicação e repetidas verificações de quantas folhas faltavam para finalizar o instrumento) em relação às tarefas do experimento. Possivelmente, variações de desempenho mesmo após a inter venção, observadas, por exemplo, em P2, P3 e P5, podem estar relacionadas com esse padrão de fuga e esquiva, o que aumenta as chances de erros por não atentar adequadamente aos problemas. Essa relação entre desempenho e motivação já foi evidenciada em estudos que reforçam respostas corretas e observam melhora de desempenho em testes de QI (e.g., Edlung, 1972).
Essas observações sugerem que em estudos futuros dois cuidados metodológicos precisam ser tomados: (1) utilizar um delineamento de LBM com sondas, o que permite reduzir a quantidade de repe tições dos testes (ver Benitez et al., 2019) e, assim, diminuir o cansaço das crianças; (2) desenvolver testes paralelos, que mensurem os mesmos compor tamentos, mas com itens diferentes em cada uma das versões (Primi, 2012). Isso permitiria reduzir o efeito aversivo das repetições de testes, pois se riam diferentes, bem como diminuiria o impacto de conversas entre os participantes sobre como responder ao teste. Adicionalmente, o uso de jogos educativos pode consistir em uma estratégia para ensinar e gerar engajamento (Panosso et al., 2015).
Uma limitação importante deste estudo foi a retirada do procedimento de pré-teste das relações de equivalência -decisão tomada para reduzir o número de testes. Ele tinha o propósito de assegurar que as crianças ainda não haviam formado a classe de equivalência, e que a adquiriram após passar pelo procedimento. Sem esse teste, não é possível afir mar que os participantes já não tivessem formado a classe de equivalência antes mesmo deste estudo.
De fato, as pequenas quantidades de erros nos treinos e testes das relações de discriminação condicional sugerem que as classes já haviam sido aprendidas, sendo que poderiam, por exem plo, estar enfraquecidas apenas. A intervenção, nessa hipótese, teria ajudado a restabelecê-las. Entender o papel que a intervenção teve sobre o desempenho é crucial porque as evidências su gerem que ela foi eficaz. Apesar das limitações do estudo, para P1, P2 e P4, ficou claro como o desempenho melhorou após a intervenção. Um estudo sobre os comportamentos de lembrar e es quecer, conduzido por Haydu et al. (2009), pode ajudar a entender a função da intervenção. Nessa pesquisa, verificou-se que classes de equivalência podem ser aprendidas e esquecidas após algum tempo e, sobretudo, que classes compostas por mais estímulos tendem a permanecer por mais tempo no repertório ou ser restabelecidas mais rapidamente do que classes com menos membros. Considere, então, que no ensino de matemática professores provavelmente trabalhem com pou cas formas de apresentação de problemas, sendo ainda menos frequente as variações de estrutura semântica em problemas escritos e posições da incógnita. Isso levaria à formação de classes de equivalência entre poucas formas de apresentação de problemas, o que facilitaria o esquecimento ou enfraquecimento da classe.
Nesse estudo, com treino sistemático para for mação dessas classes de equivalência, mediante feedback explícito e imediato ao longo de diversas tentativas, bem como o aumento de estímulos em cada classe, provavelmente houve aquisição das classes ou, no mínimo, aperfeiçoamento de classes já aprendidas. Os termos "aquisição" e "aperfei çoamento" remetem a mudanças comportamentais que caracterizam o núcleo do que analistas do comportamento definem como aprendizado (ver Goulart et al., 2012), sendo aperfeiçoamento usa do no sentido de fortalecimento de relações entre estímulos enfraquecidas, como também aumento do número de estímulos compondo a classe.
Com base nessas considerações e nos dados deste estudo, é possível afirmar que as evidências sustentam que a formação de classes de equiva lência entre diferentes formas de apresentação de problemas, posições da incógnita e estruturas semânticas de problemas escritos é importante e compõe os repertórios de somar e subtrair, que integram um repertório ainda mais amplo de re solução de problemas aritméticos. Além disso, as evidências fornecem suporte acerca da relevância de treinos de discriminação condicional para pro mover expansão dessas classes ou o restabeleci mento delas, caso tenham sido enfraquecidas pela passagem do tempo.
Outra limitação a ser considerada foi a ausên cia de um teste de generalização, conforme condu zido em outros estudos (e.g., Henklain & Carmo, 2013a,b). Esse dado teria sido importante uma vez que foi selecionado um pequeno conjunto de nú meros (entre 1 e 20) para uso nos testes e treino. É importante lembrar que a educação visa a produção de efeitos para além dos exemplos ou estímulos utilizados nas condições de ensino (Cortegoso & Coser, 2013). Nesse sentido, seria útil também a realização de uma avaliação de follow-up.
Em síntese, este estudo, com um delineamen to mais robusto do que pesquisas prévias e uma amostra do extremo norte do Brasil, apresentou evidências favoráveis sobre a eficácia da inter venção. Apesar disso, o estudo possui limitações, como a ausência de estratégias para lidar com o baixo engajamento dos participantes e a ausência de testes de (a) repertório em relação às classes de equivalência ensinadas, (b) de generalização e, (c) de follow-up. É imprescindível, portanto, que es tudos futuros sejam conduzidos de modo a sanar tais limitações.
Além disso, em função dos resultados promis sores de múltiplos estudos (Haydu et al., 2006; Henklain & Carmo, 2013a, b; Haydu et al., 2015), considera-se que trabalhos futuros possam tam bém adaptar este procedimento de ensino para o contexto de sala de aula. Assim, professores poderiam se beneficiar dos achados da pesquisa básica. Pensando nisso, ao final desta pesquisa, foi conduzido estudo-piloto que ilustra como essa adaptação poderia ser implementada.
A ideia foi simular uma aula. Os materiais uti lizados foram notebook e datashow, manejados pelo pesquisador, e um caderno de respostas para o estudante. A coleta ocorreu na mesma escola deste estudo. Havia dois tipos de atividade: associação e ditado. Participaram duas alunas de 10 anos, P7 e P8, autorizadas pelos pais via TCLE e que assi naram o TALE. Nas atividades de associação era apresentado um problema escrito no slide e, no caderno de respostas, elas tinham três problemas no formato de algarismo relativos ao slide, mas apenas um correspondia ao problema do slide, e deveria ser assinalado. No ditado, era exibido no slide um problema escrito e, no papel, a criança deveria escrever o problema correspondente em formato de algarismo. Após as crianças respon derem, era apresentada no slide a opção correta. Foram criadas 54 tarefas (36 de associação e 18 de ditado), a partir dos problemas usados neste estudo.
Para avaliar o aprendizado, foi utilizado um pré-teste seguido pelo pós-teste. Apenas P7 pa receu se beneficiar com o procedimento, sendo que P8 teve desempenho um pouco pior no pós-teste. Os resultados foram inconclusivos. Não obstante, com a continuidade dos estudos será possível avançar nessa adaptação. Espera-se que pesquisadores continuem investigando os compo nentes do comportamento de resolver problemas e propondo pesquisas metodologicamente robus tas e que contribuam com o aperfeiçoamento dos processos de ensinar e aprender.















