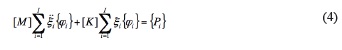http://dx.doi.org/10.15446/esrj.v20n1.54133

Numerical Simulation of Shock Response and Dynamic Fracture of a Concrete Dam Subjected to Impact Load

Lu Lu^1,2,3*, Xin Li², Jing Zhou², Genda Chen⁴, Dong Yun¹

¹ Faculty of management Engineering, Huaiyin Institute of Technology, Huai'an 223001, China
² The State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 110623, China
³ The State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023 China
⁴ The Center for Infrastructure Engineering Studies, Missouri University of Science and Technology, Rolla, Missouri 65401, USA
^* Corresponding author. E-mail: llzhxy@aliyun.com

Record
Manuscript received: 12/11/2015 Accepted for publication: 05/02/2016

How to cite item
Lu, L., Li, X., Zhou, J., & Chen, G. (2016). Numerical Simulation of Shock Response and Dynamic Fracture of a Concrete Dam Subjected to Impact Load. Earth Sciences Research Journal, 20(1). M1-M6. doi: http://dx.doi.org/10.15446/esrj.v20n1.54133

ABSTRACT

The shock response and dynamic fracture of concrete gravity dams under impact load are the key problems to evaluate the antiknock safety of the dam. This study aims at understanding the effects of impact shock on the elastic response and dynamic fracture of concrete gravity dams. Firstly, this paper uses acceleration records of a concrete gravity dam under impact to establish the correct way to determine the concrete gravity dam of the fundamental frequency and present cut sheets multi-degree-of-freedom dynamic modeling. Under strong impact loading, the constitutive relation of concrete gravity dam and the highest frequency of the impact are uncertain. So, the main advantage of this method is avoiding the use of elastic modulus in the calculation. The result indicates that the calculation method is a reliable computational method for concrete gravity dams subjected to impact. Subsequently, the failure process of dam models was numerically simulated based on ABAQUS commercial codes. Finally, this paper puts forward suggestions for future research based on the results of the analysis.

Keywords: Reservoir, Gravity dam, Underwater explosion, Failure mode, Dynamic analysis.

Introduction

Recently, the Novosibirsk Hydroelectric Plant after a report about a planted explosive, Russia has declared a state of emergency. So, this event should cause the attention of researchers and administrative departments. Hydraulic dams are critical infrastructure in geotechnical engineering. They are often designed and built to store water for drinking and irrigation in adjacent areas, to add water recreation spaces, to create a water way for the short-distance transport of people and goods across deep canyons in mountainous regions, and to regulate the river during a flood event. A water-filled dam can boost the local economy through various personal and business activities, leading to the establishment of a new community center such as a village or a town, and representing a major capital and long-term investment. On the other hand, the breaching and an accidental damage of a dam can lead to a catastrophic flood event and its chain effects such as engulfing downstream residential areas and washing away agriculture lands. Therefore, design and maintenance of dams are not only a serviceability issue but also a life-threatening matter to millions of people.

When extreme events such as earthquakes, tsunamis, hurricanes, and tornadoes took place, concrete dams can be subject to extensive shaking and wave impact. The March-11, 2011, Japan Earthquake event testified the destructive power of the earthquake-induced tsunami. Many scholars have studied the high dam subjected to earthquake action. Among these are Zhou et al. (2000), Mir et al. (1995), Kong et al. (2012). Equally, if not more important, dams are also vulnerable targets for man-made explosion events, particularly with the advent of advanced long-range and precision missile technologies. Since the September 11 attacks by terrorists, there has been increasing public concern about the threat of bomb attacks on dam structures (Federal Emergency Management Agency, 2003). Therefore, protection of dam structures against impact loads is a critical component of homeland security (Lu et al., 2013). Indeed, as respectively studied by Lu et al. (2012, 2014a, 2014b), and Zhang et al. (2014), the risk of a tall concrete dam being subjected to underwater explosion shock wave cannot be neglected.

Currently, with the development of computational techniques and numerical simulation methods, as well as commercialization of nonlinear dynamic software (e.g. ABAQUS, LY-DYNA), major developments in understanding the structural responses and failure modes of concrete structures under blast load have taken place. Many researchers have conducted comprehensive experimental and numerical investigations related to the effects of explosions on building structures(Tian et al., 2008; Jayasooriya et al., 2011), marine structures (Jin, et al., 2011; Zhang et al., 2011), underground structures (Ma et al., 2011; Li et al., (2013), and bridge structures (Hao et al, 2010; Son et al., 2011). In the modeling of transient loading, it is very critical to describe the propagation velocity of the stress waves correctly. In fact, the value of this velocity depends on the material elastic modulus that is given by the material constitutive relation. From the material point of view, concrete shows an increase in elastic modulus with the strain rate increases, a phenomenon called strain rate effect (Georgin, 2003). The relationship between concrete strength and strain rate was extensively investigated by Bischoff and Perry (1991), Georgin and Reynouard (2003), Grassl(2006) and Tai, Y.S. (2009). Because many problems of the concrete material constitutive parameters and constitutive model have not been a clear understanding, the numerical results obtained by different calculation models are very different. Moreover, the modeling of the strain rate effect on concrete is not very easy to tackle. These problems, to a great extent, comprise the uncertainty existing in the macroscopic numerical simulation.

One of the efficient methods to study the failure modes and mechanisms of structures is to carry out a large number of model experiments and obtain data from them. Considering that the experimental study has its limitations, as well as great difficulties and expensive costs for the underwater explosion test, only a small amount of data can be obtained. For example, Lu et al. (2014b) obtained only a small quantity of damage to the relationship between the state and the maximum pressure of the shock wave through model tests.

Overall, to the best of our knowledge, experimental investigations of concrete gravity dams under underwater shock wave effects have not yet been conducted to date. Concrete dams are thoroughly studied in this paper both experimentally and numerically to understand their behavior and failure modes. Specifically, this paper is to use acceleration records of the concrete structure under strong impact to establish the correct way to determine the concrete structure of the fundamental frequency and present cut sheets multi-degree-of-freedom dynamic modeling. The dams were numerically modeled to understand further their short-time failure process in the order of msec based on ABAQUS.

Examples of model tests

The same test setup and test results as presented by Lu (2012), Lu (2014a), Lu (2014b)were used in this paper which will be briefly depicted as follows. The dimension of the model dam and test layout are shown in Figure 1.

The mechanical properties of the individually tested samples and their average values are given in Table 1. Therefore, the actual material density, Young's modulus, compressive strength, and tensile strength of the small-scale model are ρ^m = 2,900 kg/m³, E^m = 355 MPa, f^cm = 205 kPa, and f^tm = 13.2 kPa, respectively.

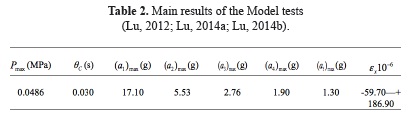
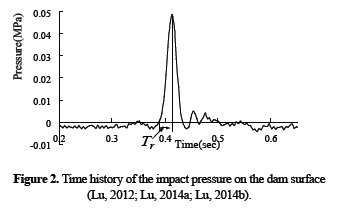
The main test results of Model test are shown in Table 2. The pressure, strain recorded and acceleration recorded are shown in Figures 2, 3 and 4.

As shown in the measured pressure-time curve, the impact load can be simplified to a triangular distribution. The failure mode and damage area are shown in Figure 5.

Note that the accelerometers and pressure sensor were not synchronized during the test. As a result, the peak accelerations seem to occur before the application of the peak pressure.

The maximum time delay among the five accelerometers is 23.44 msec. The time delay was likely caused by different periods when five hammers applied impact forces. Based on the arrival time of peak accelerations, Hammers 4 and 5 were in contact with the model dam later than Hammers 1-3.

3. Cut sheets dynamic modeling

For that, the concrete dam is divided into I unites, the governing equation for the system with I freedom is as follows:

where [M],[K] denote the mass matrix and stiffness matrix; {X}, {a} and {P} are the displacement, acceleration and force vectors, respectively. Displacement and acceleration using the vibration mode expand can be got

where is {φ_i} i-th mode vector of the system, ξ_i is general coordinate corresponding to {φ_i}.

Equation 1 after substituting Equations 2 and 3 becomes

This equation left multiplied by {φ_j}^T becomes

Use of the orthogonality of the vibration mode on the and , that is

By the Equations 5 and 6 can be got

The governing equation for ξ_i is

where superscript T denotes transformation of matrix or vector. P^i* is the generalized force the corresponding to i-th vibration mode. M^i* is the generalized masscorresponding to i-th vibration mode.

Mⁱⁱ is known quantity, so M^i* can be determined. To give expression of ξ_i, must be assumed for P^i*(t) .Therefore, three forms of the impact force-time curve were examined, as shown in Figure 6 (a-c), with the same P^max and impulse P^mT^r.

Solutions of ξ_i for Figure 6, a, b, and c, are represented by Equations 13, 14 and 15, respectively.

Because |Ẍ|_t=0 = |Ẍ|_max for Equations 13 and 14 that are inconsistent with experimental results, Figure 6 (a) and (b) are impossible. To determine the value of ξ_i must also be determined ω_0i and θ_C from the measured acceleration record. The time of acceleration extremal point(including the maximum and minimum values) t_m1^, t_m2^, t_m3^... t_mi and the time of acceleration zero point t₀₁^, t₀₂^, t₀₃^... t_0i can be obtained by the measured acceleration records. If T_r infinite,by the first type of the Equation 15, |ξ_i|_max occurs at the following times: , respectively.

By the second type of the Equation 15, the following equations can be obtained

The specific calculation process is as follows:

The Equation 17 substituting ω₀₁ of the solution to Equation 18 and t⁰¹ to determine T^r. If T^r > t^m1, then the ω₀₁ and the corresponding T^r is solution. If t^m1 <T^r, then by t^m1 and t⁰¹ from the measured acceleration records, and Equations 16 and 17 , the simultaneous solution to get ω₀₁ and T^r .

The maximum acceleration (shown in Table 2) is gradually decreased from top to bottom, which reflects the first mode characteristics of the dam.

Experiment obtained vibration mode and natural frequency, so do not need too much freedom in the calculation. For that, the model dam is divided into five unites(as shown in Fig.7.).

M_ii (shown in Fig.7.) in Kg,

It is reasonable to assume that the measured acceleration distribution is proportional to the first mode, so

for the Model test, {φ1} ^T=(1,0.323,0.161,0.111,0.074).From above

M^*₁=5.1928kg, (P^*₁)^max = 1510.016N.

For given pressure-time curve shown in Figure 6(c) the Equation 15 becomes

For given case the maximum acceleration of 1# appears in t <T^r (where T^r is rise time of the pressure pulse, as shown in Fig.6.), so ξ_i is obtained

From 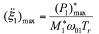and the value of ω₀₁ equal to 52.22 by Equation 18, we can get

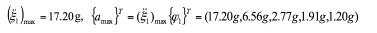
Calculation results and experimental results are in good agreement. It indicates that the cut sheets dynamic calculation model is a reliable computational model for the concrete dam subjected to impact load. The main advantage of this method is avoiding the use of elastic modulus in the calculation. Under impact loading, the constitutive relation of concrete structures and the highest frequency of the impact are uncertain. The computational work is much smaller than step by step integration.

Failure Process by Simulation

During impact tests, it is difficult, if not impossible, to observe the failure process of concrete dams over the duration of pressure pulse (∼60 msec) except at the end of the tests. On the other hand, the cut sheets dynamic model can calculate the elastic response of the dam under impact, but that cannot simulate the dynamic fracture process, and must assume that the functional form of load. Therefore, numerical simulations with a Finite Element Model (FEM) were supplemented for further understanding of the concrete dam behavior over time.

A FEM of the Model dam was established with 4-node linear tetrahedron three-dimensional (3D) elements in ABAQUS commercial codes. Due to symmetry in both boundary conditions and loads, only half of the dam was numerically modeled as shown in Figure 8. The model dam was fixed at its base. The locations of five accelerometers are also shown in Figure 8. The mechanical properties of concrete used for the Model are included in Table 1. Besides, the Poisson ratio was taken to be 0.18 in various simulations.

For convenience, the pressure-time curve in Fig. 2 was cleaned up and only the main pulse was included in simulation as shown in red line in Figure 9. After numerical treading, the peak pressure slightly increases from 48.6 kPa to 49.7 kPa due to the initial negative value of the recorded pressure time history. The horizontal stress at the location of strain gauge was calculated from the FEM under the registeredpressure. Figure 8 compares the calculated stress (black line) with the recorded pressure (red line) and the so-called "Predicted stress" (blue line) by multiplying the recorded strain by the modulus of elasticity. It is clearly seen that the three-time histories are in good agreement because the horizontal stress expects to be in equilibrium with the applied pressure at the upstream of the model dam. Therefore, the FEM is partially validated.

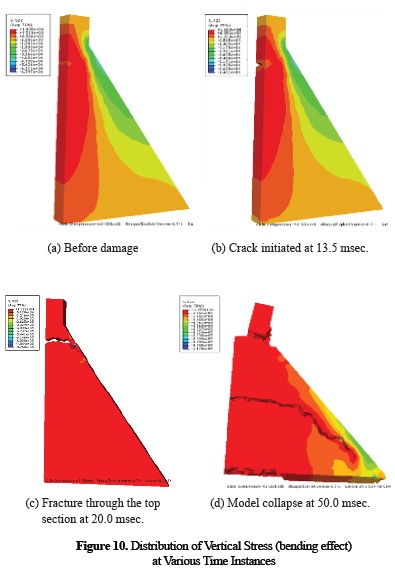
Figure 10 shows the distribution of the vertical bending stress at different time instances and the progression of structural failure. Since the maximum bending stress at 13.3 msec. exceeds the tensile strength of concrete, 18 kPa, concrete was considered to start cracking at 13.5 msec. in numerical simulations. Crack initiated at 0.57 m above the base, which is close to the fracture location observed at 0.5 m high during the testing of the Model in Table 3. At 20.0 msec, the fracture was extended to the downstream face and, by the end of pressure loading at 50.0 msec, another fracture section was fully developed across the middle of the model dam as well as at the bottom of the dam. The fracture damage at the base is similar to the pattern observed from the photo of the Model in Table 3. The fracture in the middle of model dam seems close to the damage scenario observed during the testing of Model underlarger impact loading.

In practical applications, there is no anchorage of dam foundation. It is 150 m tall (h) and 112.5 m wide (L) with a vertical upstream slope and a downstream slope of 1:0.75.

Let

P₁ is the tensile strength of concrete material. There P₁ = 0.3 MPa

P₂ isconcrete gravity against sliding stress.

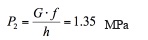
When G is the dam gravity. f=1 is the friction coefficient.

P₃ is Concrete gravity against overturning.

To simplify the calculation of the dam as a triangle, centroid dam in 1 / 3H and 2/3 L Department, the resultant moment M (T) can be obtained

where F is the uniform external force on upstream. Hydrostatic pressure P_W is expressed as:

Where ρ^w is the density of water.

If M (t) ≥ 0, when the dam starts to rotate, so

The concrete dams may be first toppled off, then fracture at their top of the damand, finally, fracture at their middle height.

The performance of concrete under impact load and static load strength and deformation have a certain difference, with the increase of loading rate, the mechanical properties of concrete exhibit different behavior, the so-called rate dependent. At present, the research work is not enough, the research data is relatively small, and the conclusions of the study are not unified. This kind of research needs mesoscopic and macroscopic numerical analysis methods(multis cale model).

Conclusions

The following conclusions can be drawn:

Under strong impact loading, the constitutive relation of concrete structures and the highest frequency of the impact are uncertain. This paper uses acceleration records of concrete structure under strong impact to establish the correct way to determine the concrete structure of the fundamental frequency and present cut sheets multi-degree-of-freedom dynamic modeling. The main advantage of this method is avoiding the use of elastic modulus in the calculation. Calculation results and experimental results are in good agreement. The computational work is much smaller than step by step integration of the finite element.

However, the cut sheets dynamic model can not simulate the dynamic fracture process, and must assume that the functional form of load. Therefore, numerical simulations with a finite element model (FEM) were supplemented for further understanding of the concrete dam behavior over time. The results of the analysis indicate that concrete damage mainly occurred at the dam head and bottom using the material property from Table 1. Concrete dams may be first toppled off, then fracture at their top of the damand, finally, fracture at their middle height.

The performance of concrete under impact load and static load strength and deformation have a certain difference, with the increase of loading rate, the mechanical properties of concrete exhibit different behavior, the so-called rate dependent. At present, the research work is not enough, the research data is relatively small, and the conclusions of the study are not unified.

Acknowledgements

This work was supported by the [the Natural Science Foundation of China] under Grant [No. 51379028,71301060], [the research Funds of the State Key Laboratory of Structural Analysis for Industrial Equipment of Dalian University of Technology] under Grant [No. GZ1409], and the [Huai'an Applied Research and Scientific and Technological Research Funds] under Grant [No. HAS2014021-4].

References and Notes

Bischoff, P.H. and Perry, S.H. (1991). Compressive behaviour of concrete at high strain rates. Materials and Structures, v. 24(6), 425-450.         [ Links ]

Federal Emergency Management Agency. (2003). Dam safety and security in the United States: a progress report on the national dam safety program in fiscal years 2002 and 2003. U.S. Department of Homeland Security.         [ Links ]

Grassl, P. and Jirásek, M. (2006). Damage-plastic model for concrete failure. International Journal of Solids and Structures, 43(22): 7166-7196.         [ Links ]

Georgin, J.F. and Reynouard, J.M. (2003). Modeling of structures subjected to impact: concrete behaviour under high strain rate. Cement & Concrete Composites, 25, 131-143.         [ Links ]

Hao, H, and Tang, E.K.C. (2010). Numerical simulation of a cable-stayed bridge response to blast loads. Part II: Damage prediction and FRP strengthening. Engineering Structures, v. 32, 3193-3205.         [ Links ]

Jayasooriya, R., Thambiratnam, D.P., Perera, N.J. and Kosse, V. (2011). Blast and residual capacity analysis of reinforced concrete framed buildings. Engineering Structures, 33(12), 3483-3495.         [ Links ]

Jin, Q. and Ding, G. (2011). A finite element analysis of ship sections subjected to underwater explosion. International Journal of Impact Engineering, 38(7), 558-66.         [ Links ]

Kong, X.J., Liu, F.H. and Liu, J. (2012). Shaking table model tests on face-slab dislocation of concrete faced rock-fill dams under earthquakes. Chinese Journal of Geotechnical Engineering. 32(2):258-266.         [ Links ]

Li, J.C., Li, H.B., Ma, G.W. and Zhou, Y.X. (2013). Assessment of underground tunnel stability to adjacent tunnel explosion. Tunneling and Underground Space Technology, v. 35, 227-34.         [ Links ]

Lu, L. (2012). Study on the Damages and Protection Decision-making of the Concrete Gravity Dam by the Action of Underwater Shock Wave. Dalian University of Technology.         [ Links ]

Lu, L., Li, X. and Zhou, J. (2013). Protection Scheme for Concrete Gravity Dam Acting by Strong Underwater Shock Wave. Advanced Science Letters, 19(1), 238-243.         [ Links ]

Lu, L., Li, X. and Zhou J. (2014a). Risk Assessment Method and Protection Goals of High Concrete Gravity Dam Subjected to Far-Field Underwater Nuclear Explosion. Advanced Materials Research, Vol. 871, 21-26.         [ Links ]

Lu, L., Li, X. and Zhou, J. (2014b). Study on Damage of High Concrete Dam Subjected to Underwater Shock Wave. Earthquake Engineering and Engineering Vibration, 13(2), 337-346.         [ Links ]

Lu, Y. (2009). Modeling of concrete structures subjected to shock and blast loading: An overview and some recent studies. Structural Engineering & Mechanics, 32(2), 235-249.         [ Links ]

Ma, G., Zhou, H. and Chong, K. (2011). In-structure shock assessment of underground structures with consideration of rigid body motion. Journal of Engineering Mechanics, 137(12), 797-806.         [ Links ]

Mir, R.A. and Taylor, C.A. (1995). An experimental investigation into earthquake-induced failure of medium to low height concrete gravity dams. Earthquake Engineering and Structural Dynamics, 24(3), 373-393.         [ Links ]

Son, J. and Lee, H.J. (2011). Performance of cable-stayed bridge pylons subjected to blast loading. Engineering Structures, v. 33, 1133-1148.         [ Links ]

Tai, Y.S. (2009). Flat ended projectile penetrating ultra-high strength concrete plate target. Theoretical and Applied Fracture Mechanics, v. 51 (2), 117-128.         [ Links ]

Tian, L, and Li Z.X. (2008). Dynamic response analysis of a building structure subjected to ground shock from a tunnel explosion. International Journal of Impact Engineering, 35(10), 1164-78.         [ Links ]

Zhang, A., Zhou, W., Wang, S. and Feng L. (2011). Dynamic response of the non-contact underwater explosions on naval equipment. Marine Structures, 24(4), 396-411.         [ Links ]

Zhang, S., Kong, Y. and Wang, G. (2014). A comparative study on the dynamic response of concrete gravity dams subjected to underwater and air explosions. Journal of Performance of Constructed Facilities, Vol. 33(17), 47-54.         [ Links ]

Zhang, S., Wang, G., Wang, C., Pang, B. and Du, C. (2014). Numerical simulation of failure modes of concrete gravity dams subjected to underwater explosion. Engineering Failure Analysis, 36, 49-64.         [ Links ]

Zhou, J., Lin, G., and Zhu T. (2000). Experimental investigation into seismic failure of high arch dams.Journal of Structural Engineering. 126(8), 926-935.         [ Links ]