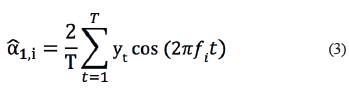1. Introduction

Time series models are often used in hydrology studies to model streamflow series in order to make predictions and to generate synthetic series which are inputs for the analysis of complex water resources systems (see, for example, ^{Salas et al., 1980}, 1982; ^{Hosking, 1984}; ^{Hipel & McLeod, 1994}; ^{Montanari et al., 1997}; ^{Hasebe et al., 2000}). In many studies, hydrologists also use time series data to display the amount of rainfall that has fallen in a region for the past day, year or a period of 10 years (see for example, ^{Guimaraes & Santos, 2011}, and ^{Lee & Lee, 2000}).

Modeling hydrological variability is very important in the planning and management of water resources. Many aspects of the hydrologic cycle could be described by time series data. Researchers, usually use time series data to evaluate the resources of a water basin. Important variables related to streamflow and watershed describes streamflow properties such as monthly flows or streamflow parameters. Assuming a specified time series model, we usually could estimate the streamflow parameters using a classical or a Bayesian inference approach.

Different time series models as ARMA and higher orders of MA models have been used by some authors when considering hydrologic regionalization of watersheds (see for example, Chiang et al., 2002 a, b; ^{Wang et al., 2015}). ^{Valipour et al.(2013)} studied annual runoff time series in Dahuofang reservoir, in northeast China, using autoregressive integrated moving average (ARIMA) models coupled with ensemble empirical mode decomposition (^{Wu, Z., & Huang, N. E., 2009}). Spectral analysis and forecasting of hydrological time series has also been considered (^{Marques et al., 2006}), including geostatistical applications (^{Robin et al., 1993}) and climate change investigations (^{Lall and Mann, 1995}).

Considering hydrological time series, the monthly streamflow series typically have a periodic behavior in the mean and variance and in general, periodic autoregressive models are used in de analysis of the data (see, for example, ^{Modal & Wasimi, 2006}). In this situation, usually it is assumed that the series flow has a normal or log-normal distribution (see for example, ^{Tesfaye et al., 2006}; ^{Wang et al., 2009}).

The behavior of meteorological time series is similar to the behavior of hydrological time series. In this case, given that the relative air humidity is a random variable with values given in the open interval (0, 1), we could assume a beta distribution to analyze the data. Another possibility to analyze the data set is to consider a transformation of the data and to assume a normal distribution for the transformed data. As a special case, we could assume a logistic transformation.

In this paper, a more general model is considered in the analysis of the hydrological or meteorological time series conditional to the historical available information: it is assumed that the data is generated from a normal, a gamma or a beta distribution, with conditional mean and variance, given respectively, by E [Y_t|Y_t-1] and V [Y_t| Y_t-1], where the index tis related to time. Thus a general model is proposed to analyze hydrological or meteorological time series, assuming that the observations are generated from a continuous biparametric exponential family of distributions.

As an illustration and motivation for the use of the proposed models, we first consider as a first example, a data set consisting of the time series of monthly averages of natural streamflows, measured in the year period ranging from 1931 to 2010, in Furnas hydroelectric dam, located in southeastern Brazil. This time series is shown in Figure 1. From this Figure, we observe that the streamflow series have a periodic behavior in the mean and variance and in this case, general periodic autoregressive models are usually assumed in the analysis of the time series data (^{Modal & Wasimi, 2006}).

Figure 1 Time series of monthly averages of natural streamflows. 

To take into account the heteroscedasticity in the time series of streamflows showed in this first example, we propose a new model which assumes seasonal and autoregressive terms in the modeling of the mean and variance parameters. In this way, we propose a periodic and heteroscedastic model, in which the variance also presents an autoregressive structure.

As a second example, we consider another time series with behavior similar to the assumed hydrological time series presented in the first example, consisting of a meteorological time series given by weekly averages of air humidity, measured in the city of Rio Claro, São Paulo state, Brazil (Figure 2). In this case, given that the relative air humidity is a random variable with values in the open interval (0, 1), it is assumed a beta distribution in the analysis of the data. In this case, we propose a jointly modeling for the mean and for the variance of the data considering beta regression models, including seasonal and autoregressive terms in both regression models

Figure 2 Air humidity time series data. 

The paper is structured as follows: in section 2, it is introduced the seasonality analysis of the time series. In section 3, it is proposed seasonal autoregressive models. In section 4, it is presented the results of the analysis of the hydrological time series obtained using the proposed models assuming normal and gamma distributions. In section 5, it is presented the results of the analysis of air humidity time series. Finally, in section 6 it is presented some conclusions and future research topics.

2. A period model

In this section, we introduce a new modeling approach including seasonality terms in the model which better describes time series of monthly averages of natural stream flows, denoted by Y _t In the first case, we consider the time series data related to the monthly averages of natural streamflows in Furnas hydroelectric dam (Figure 1). A preliminary spectral analysis is developed for this time series to determine the time periods to be considered in the mean and variance model formulations. Thus, if in the spectral analysis, the number of observations is T = 2q + 1, where q is a positive integer number, the Fourier time series model given by:

is to be fitted by the data, where f_i = i/T is the ith harmonic of the fundamental frequency 1/T and, α_1,i and α_2,i, i = 1,...,q, are the related coefficients and e_t is an error term assumed to have the first and second moments given respectively by and to be uncorrelated, that is, .

Considering the n observations of the time series, the least square estimates of the coefficients α0 and (α1,i, α2,i), i = 1,...q, are obtained from the equations:

Based on these estimates, the intensity of each frequency is calculated by:

Observe that the highest frequency is 0.5 cycle per month (time interval) since the smallest period is 2 months. This preliminary analysis of the intensities of frequencies allows us to reduce the number of harmonics considered in the time series included in the model, considering only those frequencies that have higher intensities (^{Marques et al., 2006}). For a series consisting of 80 years of observations (that is 960 months) we would have 480 harmonics, but considering this preliminary analysis, we could reduce the number of harmonics to three or four. Usually, in the case of monthly time series, these periods are given by periods of 6 and 12 months. These periods will be discussed in Section 4, where the specification of the parameters related to the periods is made simultaneously with the specification of the parameters for the autoregressive models assumed for the mean and variance in the time series formulations to be introduced in Section 3. If some of these parameters show to be not significant after a preliminary statistical analysis, the terms related to these parameters are deleted from the model to develop a further analysis. The final decision on which harmonics should be included in the model must be made considering some criteria for model selection or hypothesis test on the fitted coefficients α1,i,. and α2,i.

3. The proposed seasonal autoregressive model

In hydrological or meteorological time series, we usually assume that the observations of interest are generated from a conditional continuous probability distribution function. As special cases, we could assume that the observations are generated from standard normal, gamma, beta or exponential conditional density functions, denoted by f (yt |Ht-1), t = 1,2,...,T , where Ht-1 is the available information up to time t - 1 and thus Yt has conditional means and variances given respectively by μt = E (Yt |Ht-1) and ht = Var(Yt|Ht-1), following the models:

where , is the vector of parameters for the mean model and 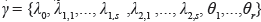is the vector of the parameters for the variance model, ƒ_i = i/T the ith harmonic of the fundamental frequency 1/T. In this paper, the parameters of the proposed models are estimated under a Bayesian approach.

In order to illustrate the proposed methodology, we also include the regression equations relating the mean and variance parameters to the assumed covariates assuming gamma and beta distributions for the data. In this way, we have, the following modeling steps:

In this reparameterization, where the autoregressive seasonal beta regression models have the conditional mean and variance model given by the equations (6) and (7).

Special cases of this model could be easily obtained from this general model. A first model is given by a seasonal regression mean model, with mean given by (6) and autoregressive variance not considering the presence of seasonal terms. A second model, also a seasonal mean model, is given assuming the mean given by (6) and a seasonal variance model not considering the presence of autoregressive terms. A third model, is given by an autoregressive mean model and a variance model, not considering the presence of seasonal terms in the mean and in the variance. A fourth model, is given by an autoregressive model, with constant variance.

4. Hydrological time series

In this section we consider an analysis of the Furnas dam hydroelectric hydrological time series dataset, introduced in Section 1, assuming seasonal autoregressive conditional heteroscedastic models.

The first step in the proposed analysis is to determine the period for the harmonics of higher intensity in the spectral analysis of the streamflows data. In this way, we note in Figure 3 that the harmonics of higher intensity (I) corresponds to the cycle (1/f_i) of 6 and 12 months, given that the periodogram shows that this time series contains two cosine-sine peaks at these frequencies. There are other very small peaks in this periodogram, possibly caused by noise components. Thus, the seasonal terms to be included in the mean equation model of the streamflow series are given by cos(27πt/6), sin(27πf/6), cos(27πt/12) and sin(27πt/12). The periodogram of a time series can be obtained using the R-function periodogram (x, method,..) of the library "GeneCycle" (^{Ahdesmaki et al., 2012}). Other statistical software can be used to estimate the periodogram of a seasonal time series, for example, MathLab or the statistical software Excel-XLStat.

Figure 3 Periodogram of natural streamflows time series. 

Many autoregressive models could be assumed to analyze this data set. As special cases, we will assume, in section 4.1, a seasonal conditional normal distribution for the data and, in section 4.2, a seasonal conditional gamma distribution for the data. In order to apply the Bayesian methodology, independent normal prior distributions N(0,10^k), with k = 2, are assumed for the regression parameters associated with the seasonal terms. For the other parameters of the model, we assume independent normal prior distributions N(0,10^k), with k = 5. It is important, to point out that non-informative prior could be used (see, for example, Geman, 2006), but in our case, the obtained results are very similar.

Since we are using the free available software WinBugs to simulate samples for the joint posterior distribution of interest in all assumed models, which only requires the introduction of the joint distribution for the data and the prior distributions for all parameters of the model, we will not present in this paper the required full conditional posterior distributions for all parameters needed in the Gibbs sampling or the Metropolis-Hastings algorithms.

4.1. Normal seasonal time series

In this section, we present the results of the Bayesian analysis for the time series of monthly averages of natural streamflows, measured in the period ranging from 1931 to 2010, considering the dataset related to a hydroelectric dam introduced in Section 1, assuming jointly modeling for the mean and variance, assuming a normal model for the data. From the model given by equations (6) and (7), many autoregressive models were considered in the analysis of the data, and the model with smallest DIC (deviance information criterion, introduced by ^{Spiegelhalter et al, 2002}) value was given by the heteroscedastic normal regression model with conditional mean and variance structures given respectively by,

Samples of the joint posterior distribution of interest were simulated using standard MCMC (Markov Chain Monte Carlo) methods and the free available WinBugssoftware (^{Spiegelhalter et al, 2003}). In each of the cases, many samples were generated starting from different initial values. All of them showed the same behavior, after a small burn-in period consisting of 3,000 or 5,000 generated samples. Convergence of the simulation algorithm was observed from trace plots of the generated Gibbs samples.

For the model given by equations (10) and (11), the value of the logarithm of the likelihood function evaluated at the obtained estimates for the parameters of the model was given by -2logL=10479.200 and the obtained DIC value was DIC=10876.500. Monte Carlo estimates of the posterior means for each parameter based on the generated Gibbs samples and their respective standard deviations are given in Tables 1 and 2, including both autoregressive and seasonal terms in the conditional mean and variance terms.

Table 1 Normal model: Bayesian estimates for the mean parameters. 

Table 2 Bayesian estimates of the variance parameters. 

As an illustration of the performance of the proposed model, Figure 4 shows the agreement between monthly averages of natural streamflows and the fitted mean estimate. At the same time, Figure 5, depicting of the fitted squared root of the expected volatility shows periods of high volatility around of the months 200, 400, 600 and 800, as observed in the data behavior.

Figure 4 Monthly averages of natural streamflow and normal fitted mean estimates. 

Figure 5 Normal fitted squared root of the expected volatility. 

4.2 Gamma seasonal time series

In this section we present the results of the Bayesian analysis for the time series for monthly averages of natural streamflows, measured in the period 1931 to 2010, in Furnas hydroelectric dam, assuming joint modeling for the mean and variance autoregressive gamma models, that is, we assume that the observations of the interest are generated from a conditional gamma density function given by f (y _t \H _t-1 ), where H _t-1 ) is the information up to time t - 1 and Y _t has conditional mean and conditional variance given respectively by ( _t = E(Y _t | H _t-1 ) and , and defined by (10) and (11). For this model, the logarithm of the likelihood function evaluated at the estimates for the parameters of interest is given by -2logL=10649 and the DIC value is given by 10862.300. Using the DIC criterion to discriminate the two models (normal seasonal time series and gamma seasonal time series), we observe better fit of the data for the gamma seasonal time series model, since we have smaller DIC value for this model.

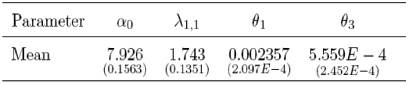
The Bayesian estimates of the posterior means for the parameters together with the corresponding standard deviations are given in Tables 3 and 4.

Table 3 Gamma model: Bayesian estimates for the mean parameters. 

Table 4 Gamma model: Bayesian estimates for the variance parameters. 

Although the mean parameter estimates given in Tables 1 and 3, and variance parameter estimates given in Tables 2 and 4, show some agreement between conditional normal and conditional gamma regression parameter estimates, the DIC value of the conditional gamma model is smaller than that of the conditional normal heteroscedastic models, showing that the class of gamma models is better to fit the monthly averages of natural streamflow data.

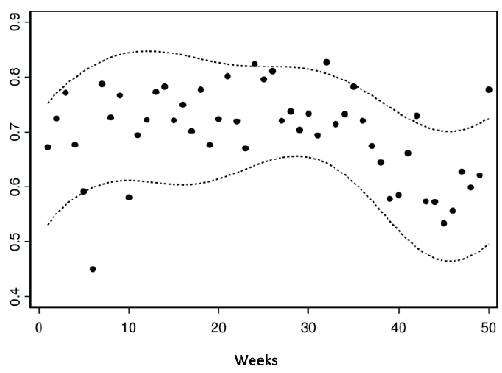
In order to determine the forecasting performance of the proposed Gamma seasonal model, we fit this model to the first 910 observed values of the Furnas dam hydrological time series, in order to predict the temporal behavior over the 50 last months. The parameter estimates agree with those reported in tables 3 and 4. Figure 6 shows that this model has good performance in predicting monthly averages of natural streamflows. This figure shows the 90% prediction interval for the variable of interest in these last weeks in dashed lines, and the observed values of natural streamflows in black points.

Figure 6 Monthly averages of natural streamflow. 

5. Beta mean and variance seasonal models applied to air humidity time series

In this section it is assumed that the time series data are generated from a beta distribution, B(p _i ,q _i ), with conditional mean and variance given, respectively, by (6) and (7). To illustrate the application of the proposed model to be fitted by the data set, we consider the time series of weekly averages air humidity, measured in Rio Claro city, located in southeastern of Brazil, from 18/10/2002 to 08/10/2008. This time series, introduced in section 1, is shown in Figure 2.

As in Section 4, the first step in the proposed analysis is to determine the period of harmonics of higher intensity in the spectral analysis of the humidity data. From the corresponding periodogram, Figure 7, we note that the harmonics of higher intensity corresponds to the cycle (1/f _i ) of 26 and 52 days. As in the analysis of streamflow data, the periodogram shows that this time series contains two cosine-sine peaks at these frequencies, two larger peaks, and other very small peaks, possibly caused by noise components. Thus, the seasonal term to be included in the mean equation model of the streamflow series are given by: cas(27πf/26), sin(2πtl26), cas(27πf/52) and sin(2πt/52).

Figure 7 Periodogram of humidity Times series. 

5.1. Seasonal mean and conditional variance models

In this section, double seasonal beta repression models are proposed to analyze the air humidity time series data introduced in Section 1. In this way, we conclude that the best beta seasonal mean and variance model is the one where the mean and dispersion regression structures are given by:

Assuming independent normal prior distributions N(0,100) for the regression parameters α₀ and α₁ for i = 1,2 and for λ₀ and λ₂ for i = 1,2. To fit the model 20,000 samples of the joint posterior distribution for the parameters of the model were also generated using the MCMC methods and the WinBugs software (^{Spiegelhalter et al, 2003}). Monte Carlo estimates for the posterior means of each parameter were obtained from the final simulated Gibbs sample, after an initial burn-in sample period of 2000 samples. This "burn-in sample" was discarded to eliminate the effect of the initial values in the iterative procedure. After this "burn-in sample" period we simulated another 20,000 Gibbs samples choosing every 20 iteration to get approximately non-correlated samples, which gives a final sample of size 1,000 used to get the posterior summaries of interest. The posterior summaries of interest are given in Table 5, for the mean regression parameters, and in Table 6, for the variance regression parameters.

Table 5 Beta model: Bayesian estimates for mean parameters. 

Table 6 Beta model: Bayesian estimates for the variance parameter. 

The logarithm of the likelihood function evaluated at the obtained estimates for the parameters of the model is given by log L = -853.082 and the DIC criterion has a value equals to -825.525. In Figure 8, we observe a good agreement between data and the fitted mean, showing the good performance of the proposed model to analyze this data set. Figure 9, revels a good agreement for the variances, where smaller means are accompanied by smaller variance. This behavior also was observed in the original time series. That is, we conclude that this model fits by the time series data very well.

Figure 8 Air humidity time series data (continuous line) and fitted mean (diseased line) for double seasonal model. 

Figure 9 Fitted conditional variance time series. 

To determine the forecasting performance of the proposed models, we fit the seasonal beta autoregressive model to the first 282 observed values of the air humidity time series data, in order to predict the time behavior in the 30 last weeks. Figure 10 shows the 90% prediction interval for these last weeks, in dotted lines and the observed values of natural streamflows in black points.

Figure 10 Forecasting humidity time series. 

6. Concluding Remarks

In this paper, we introduce a new class of time series models assuming continuous random variables within the exponential family applied to hydrological and meteorological data. Special cases of this proposed methodology were considered assuming, normal, gamma and beta distributions. These new models could be of great interest to analyze hydrological and meteorological data, since the original data usually could not be fitted assuming the standard modeling approach for the means of the data or assuming standard distribution assumptions for time series data. Other important practical point: in practical work, usually it is required to model simultaneously the mean and the variance depending on a vector of parameters to get better predictions and to discover the real behavior of a hydrological or a meteorological time series. With this modeling approach, we could get better inferences as it was observed in the illustrations introduced in this paper. This approach usually is not considered by hydrological or meteorological researchers using standard available software for hydrology or meteorology time series. In this way, the use of Bayesian methods is a good alternative to get accurate inferences and predictions, especially using MCMC methods, since these inference methods are not based on asymptotical results as its common with standard existing classical approaches based on maximum likelihood estimation procedures. Other important point: under the use of a Bayesian approach, we could consider informative prior distributions when is available prior opinion of experts in hydrology and meteorology. This means, better predictions. It is also important, to point out that the computational work needed in the simulation of samples of the joint posterior distribution to get the posterior summaries of interest is greatly simplified using standard existing softwares like the WinBugs software. The proposed methodology was illustrated considering two Brazilian data sets: a hydro- logical time series and a meteorological time series. A final point of relevance for the results of this paper: new statistical models for time series to model climatic variables leading to better inferences and predictions based on data from hydrology and meteorology can be of great practical interest, especially with the large climate changes that have been observed in the world in recent decades.

To determine the performance of the proposed models, an extensive comparison with other models proposed in the literature should be developed. However, in order to compare the performance of the gamma seasonal models with in a model without a seasonal component, we fit the autoregressive model Ar(3), for which the DIC value was 11990, bigger than the DIC value of the fitted gamma seasonal model. The sum of square residuals obtained from applying the AR(3) model is also bigger than that for the proposed models. For the AR(3) model, the sum of square residuals is 65679347 and for the proposed model it is 52976950. Finally, we fit the Ar(3) model to the humidity data, for which the DIC value was -774.550, bigger than -825.525, the BIC value of the fitted beta seasonal model. The sum of square residuals obtained from applying the AR(3) model to the humidity data is 17.1565, larger than the DIC value (1.3786) of the proposed models.