ARTÍCULO ORIGINAL

 

Estimación bayesiana de una proporción bajo error de estimación asimétrico

 

Bayesian estimation of a proportion under an asymmetric observation error

 

Estimação bayesiana de um erro de estimação em relação assimétrica

 

Juan Carlos Correa Morales¹, Juan Carlos Salazar Uribe²

¹ Doctor en Estadística, jccorrea@unal.edu.co, profesor, Universidad Nacional de Colombia, Medellín Medellín, Medellín-Colombia.

² Doctor en Estadística, jcsalaza@unal.edu.co, profesor, Universidad Nacional de Colombia, Medellín-Medellín, Medellín-Colombia.

 

Recepción: 02-may-2011. Modificación: 10-may-2012. Aceptación: 16-may-2012

Se aceptan comentarios y/o discusiones al artículo

 

---

Resumen

El proceso de estimación de una proporción relacionada con una pregunta que puede ser altamente sensible para el encuestado, puede generar respuestas que no necesariamente coinciden con la realidad. Para reducir la probabilidad de respuestas falsas a este tipo de preguntas algunos autores han propuesto técnicas de respuesta aleatorizada asumiendo un error de observación asimétrico. En este artículo se presenta una generalización al caso donde se asume un error simétrico lo cual puede ser un supuesto poco realista en la práctica. Se deduce la función de verosimilitud bajo el supuesto de error de estimación asimétrico. Con esto se pretende que en la práctica se cuente con un método alternativo para reducir la probabilidad de respuestas falsas. Asumiendo distribuciones a priori informativas se encuentra una expresión para la distribución posterior. Puesto que esta última no tiene una expresión cerrada es necesario usar el muestreador de Gibbs en el proceso de estimación. Esta técnica se ilustra usando datos reales sobre consumo de drogas recolectados por la Oficina de Bienestar de la Universidad Nacional de Colombia, Sede Medellín.

Palabras claves: Estimación bayesiana, distribución binomial, probabilidad de respuesta falsa, sustancias sicoactivas.

---

Abstract

The process of estimating a proportion that is associated with a sensitive question can yield responses that are not necessarily according to the reality. To reduce the probability o false response to this kind of sensitive questions some authors have proposed techniques of randomized response assuming a symmetric observation error. In this paper we present a generalization of the case where a symmetric error is assumed since this assumption could be unrealistic in practice. Under the assumption of an assymetric error the likelihood function is built. By doing this we intend that in practice the final user has an alternative method to reduce the probability of false response. Assuming informative a priori distributions an expresion for the posterior distribution is found. Since this posterior distribution does not have a closed mathematical expression, it is neccesary to use the Gibbs sampler to carry out the estimation process. This technique is illustrated using real data about drug consumptions that were collected by the Oficina de Bienestar from the Universidad Nacional de Colombia at Medellín.

Key words: Bayesian estimation, Binomial distribution, Probability of false response, psychoactive drugs.

---

Resumo

O processo da estimação de uma proporção relacionada a uma questão que pode ser muito sensível para o entrevistado, pode gerar respostas que não coincidem necessariamente com a realidade. Para reduzir a probabilidade de respostas falsas a estas questões, alguns autores propuseram técnicas de resposta aleatórias, supondo um erro de observação assimétrico. Neste artigo apresentamos uma generalização do caso onde um erro simétrico é considerado, o qual pode ser uma hipótese irrealista na prática. Logo, deduzimos a função de verossimilhança sob a hipótese de erro de estimação assimétrico, a qual é usada na prática como um método alternativo para reduzir a probabilidade de respostas falsas. Assumindo a prioris informativas é achada uma expressão para a distribuição a posteriori. Já que o último não tem uma expressão fechada é necessário utilizar a amostragem de Gibbs no processo de estimação. Esta técnica é ilustrada com dados reais coletados no uso de drogas pelo Gabinete de Ação Social da Universidade Nacional da Colômbia, Medellín.

Palavras chaves: Estimação bayesiana, distribuição binomial, probabilidade de resposta falsa, substâncias psicoativas.

---

 

1 Introducción

Cuando se trata de estimar una proporción no es poco común tener registros equivocados en la muestra Bernoulli. Esto puede ocurrir por muchas razones. Por ejemplo, en una encuesta una persona puede responder de manera intencional una pregunta sensible sobre consumo de drogas, de homosexualidad, o sobre política. En otras situaciones la persona puede no recordar un evento pasado. Para algunas situaciones donde el sujeto encuestado puede sentirse comprometido o expuesto por la respuesta a una pregunta sensible y donde se pueda presentar la situación de dar una respuesta falsa, Warner [1, 2] propuso un procedimiento conocido como el de la respuesta aleatorizada. Este procedimiento también ha sido estudiado por otros autores tales como, Greenberg [3], Lamb y Stem [4], Campbell [5], Tracy y Fox [6], Miller [7], Bourke y Dallenius [8], [9], [10, 11], [12]. Por otra parte, Winkler y Gaba [13] proponen un método de estimación bayesiana de la proporción verdadera basado en datos que pudieran haber sido recolectados usando el método de respuesta aleatorizada. Este método asume, entre otros supuestos, que el error de observación es simétrico lo cual puede no ser un supuesto realista en la práctica. Por ejemplo, es más frecuente que una persona niegue tener una cierta característica cuando en realidad la tiene a que una persona acepte tenerla solamente con el fin de despistar o burlar al encuestador, es decir a una pregunta tal como ¿Consume usted alguna sustancia alucinógena? una persona que en realidad lo hace tiene una alta probabilidad de negarlo mientras que una persona que en realidad no usa este tipo de sustancias podría responder afirmativamente pero no parece razonable asumir que ambas probabilidades sean iguales. Por esta razón, para estimar la proporción, parece más conveniente asumir que el error de observación es asimétrico. Ahora, puesto que tratar de averiguar a partir de la muestra quienes respondieron correcta o incorrectamente no parece ser una tarea fácil, asumir distribuciones a priori informativas para estas tasas de falsa respuesta o clasificación puede ayudar a modelar esta incertidumbre. El problema de la clasificación errónea es un problema que no pierde vigencia como se puede evidenciar en la literatuta reciente (Stamey et al. [14], Boese et al. [15], Lee y Byun [16] y Rahardja y Zhao [17]) donde se aborda el problema desde distintas perspectivas y escenarios muestrales diversos.

El propósito de este trabajo es mostrar una estrategia de estimación bayesiana de la proporción verdadera asumiendo que el error de observación no es simétrico. Para alcanzar este objetivo se exponen primero aspectos relacionados con el trabajo de Winkler y Gaba. Luego se generaliza este trabajo para permitir errores de observación asimétricos. Finalmente, se ilustra la técnica usando datos reales sobre consumo de drogas en la Universidad Nacional de Colombia, Sede Medellín.

 

2 Metodología

En esta sección se detalla la metodología de análisis estadístico propuesta para el problema de la obtención de la proporción bajo el supuesto de error asimétrico. Esta metodología no se ha presentado en la literatura y constituye un aporte original de este trabajo.

2.1 El método de respuesta aleatorizada

El método de respuesta aleatorizada es un método que se usa en encuestas y entrevistas estructuradas. Fue propuesto en primera instancia por Stanley L. Warner [1]. Este método permite al encuestado responder a preguntas sensibles (por ejemplo comportamiento criminal o sexualidad) al tiempo que se mantiene la confidencialidad. La pregunta sensible se dicotomiza y el azar decide, sin el conocimiento del encuestador, cual de las dos alternativas se va a responder de manera honesta. Por ejemplo, se le pide al encuestado que antes de responder lance un dado y que responda una de las dos alternativas solo si obtiene un 6, en caso contrario debe responder la otra alternativa. El encuestador obtiene un Si o un No sin saber a cual de las dos alternativas se le asignó una de estas respuestas.

Si se denota por p la verdadera probabilidad que se trata de estimar y si X₁, X₂, · · · , X_n es una muestra aleatoria de una Bernoulli(p), la verosimilitud de la muestra estará dada por:

y si π(p) denota la distribución a priori, entonces la distribución posterior será π (p|X₁, X₂, · · · , X_n) L (p|X₁, X₂, · · · , X_n) π(p). Es común seleccionar como a priori una distribución conjugada, que en este caso es una distribución beta, digamos Beta (α, β), lo cual nos lleva a una posterior de la misma familia, Beta (α + Xi, β + n - Xi). En esta situación es fácil realizar inferencias acerca de p.

Si λ denota la probabilidad de que un sujeto esté mal clasificado, entonces la verosimilitud será:

L(p, λ|y, n) = [p(1 - λ) + (1 - p)λ]^y[pλ + (1 - p)(1 - λ)]^n-y

Winkler y Gaba (1990) proponen la siguiente distribución a priori para p y λ

la cual es el producto de dos beta. Ellos asumieron independencia entre p y λ, lo cual puede no ser realista en muchas situaciones, por ejemplo, una persona puede responder positivamente si ha tenido una conducta antisocial que puede ser practicada por una gran parte de la población, por ejemplo pasarse un semáforo en rojo. Bajo este modelo ellos llegan a la siguiente distribución posterior

donde

con

Esta es una mezcla de productos de distribuciones beta.

Gaba [18] considera la estimación en un proceso de Bernoulli con error, pero asume dependencia entre el nivel del error y la proporción de interés. La densidad conjunta a priori de p y λ puede expresarse como

π(p, λ) = π(p)π(λ|p)

Gaba seleccionó una beta con parámetros α y β para la distribución marginal a priori de p y asumió que el parámetro de ruido es modelado como

λ = cg(p),

donde 0 ≤ λ ≤ 1, g(p) es una función no creciente de p (lineal o no) tal que 0 ≤ g(p) ≤ 1, con g(0) = 1 y c es una variable aleatoria en [0, 1]. La distribución de c la modeló como una beta con parámetros α_c y β_c. La distribución de λ/g(p) dado p sigue una Beta(α_c, β_c). Por lo tanto la distribución de λ condicionada en p es una beta re-escalada en el intervalo [0, g(p)]. Si g(p) = 0, esta beta re-escalada es degenerada en cero, o sea P(λ = 0|p) = 1. La a priori conjunta de p y λ es entonces

donde 0 ≤ p ≤ 1, 0 ≤ λ ≤ g(p) y 0 < g(p) ≤ 1. Gaba propone trabajar con g(p) seleccionada de

donde k > 0 y m ≥ 0.

La distribución posterior será:

donde

donde π(p|y, n, t, i) es una distribución beta con parámetros α + n - t + i y β + t;

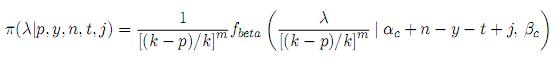
y

con φ como una constante de normalización dada por

y

2.2 Estimación asumiendo error de observación asimétrico

Ahora, si el sujeto encuestado tiene una probabilidad diferente de ser mal clasificado cuando es un "éxito", llamela λ₁, que cuando es un "fracaso", la cual se denotará λ₂, la verosimilitud será entonces:

L (p, λ₁, λ₂|y, n ) = [p(1 - λ₁) + (1 - p)λ₂]^y [1 - p(1 - λ₁) + (1 - p)λ₂]^n-y

Si π (p, λ₁, λ₂) denota la distribución a priori, entonces la distribución posterior será:

π (p, λ₁, λ₂|y, n ) L (p, λ₁, λ₂|y, n ) π (p, λ₁, λ₂)

Como el parámetro de interés es p, se debe calcular la distribución marginal. Esta se halla como:

Asumiendo independencia, π (p, λ₁, λ₂) = π_p(p)π_λ1(λ₁)π_λ2(λ₂). En este caso se puede asumir, por ejemplo, que p se distribuye de acuerdo a una Beta(α₀,β₀), y λ₁ y λ₂ de acuerdo a normales truncadas en el intervalo (0, 1) con parámetros µ₀ y σ₀. Observe que la distribución posterior así formulada no admite una solución analítica y por lo tanto se deben recurrir a métodos numéricos para poder muestrear de ella. Una alternativa que ha probado ser efectiva es el muestreador Gibbs.

2.3 El muestreador Gibbs

La solución analítica de problemas bayesianos es en muchos casos imposible. De hecho, cuando las distribuciones posteriores son de alta dimensión, las soluciones analíticas o las numéricas comúnes no se pueden obtener. Esto ha llevado al desarrollo e implementación de una metodología conocida como MCMC (Monte Carlo Markov Chain), la cual ha permitido un desarrollo significativo en la solución de problemas estadísticos complejos. Los métodos MCMC son algoritmos iterativos que se utilizan cuando el muestreo directo de una distribución de interés ξ no es factible. En especial, la limitación en el uso de distribuciones a priori se ha superado. Existen dos problemas mayores que rodean la implementación e inferencias de los métodos MCMC.

1. El primero tiene que ver con la convergencia y

2. el segundo con la dependencia entre las muestras de la distribución posterior.

Uno de los algoritmos más usado bajo esta metodología es el denominado muestreador Gibbs (Gibbs Sampler [19])

Muestreador Gibbs Para obtener una muestra de la distribución conjunta p(θ₁, · · · , θ_d) el muestreador Gibbs [19] itera sobre este ciclo:

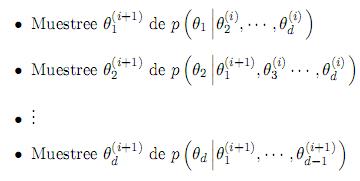
Este proceso se detiene tan pronto la cadena de Markov alcanza la distribución límite. Sin embargo, en la práctica esta convergencia puede ser muy lenta y el mayor problema es saber si se ha logrado una convergencia razonable (esto se conoce como un "burn-in"). Por lo tanto las muestras obtenidas hasta el punto de "burn-in" son descartadas.

Una ventaja de usar métodos Monte Carlo Markov Chain (MCMC) en el contexto del problema que aquí se trata es que se estima la probabilidad del evento de interés corrigiendo la falsa respuesta que se puede obtener en ambos sentidos (falsos positivos o falsos negativos). Ahora bien, como el problema se aborda desde el punto de vista bayesiano, ya que se asumen distribuciones a priori informativas generales sobre ambos casos, la presencia de tres parámetros de interés puede ser complejo desde lo analítico porque no se impone una estructura conjugada para la proporción de falsos positivos y falsos negativos. Es por esto que resulta recomendable usar MCMC no solo por la disponibilidad del software sino por la eficiencia demostrada del muestreador de Gibbs. La principal desventaja de los métodos MCMC, es que las muestras son correlacionadas y en muchos casos no existe garantía de que la cadena converja a la distribución límite. Otra alternativa al MCMC es la simulación directa en la cual se asumen muestras independientes.

 

3 Resultados

A continuación se presentan los resultados de aplicar la metodología clásica, la cual no tiene en cuenta la posibilidad de error en la respuesta, y la bayesiana, la cual si tiene en cuenta este error, para obtener la proporción. Para esto se usarán datos recolectados por La Oficina de Bienestar de la Universidad Nacional de Colombia, Sede Medellín. En la encuesta que se realiza entre estudiantes que van a empezar su ciclo académico a nivel de pregrado, se formulan preguntas sobre si el estudiante consume o no sustancias sicoactivas, tales como la marihuana. Aunque el cuestionario es autoformulado, se esperaba que algunos estudiantes respondan falsamente a esta pregunta, unos por temor o no aceptación de su situación, en cuyo caso la respuesta es NO; algunos otros responden SÍ como medio de burlar la pregunta. Para el año 2008, primer semestre, se registraron los siguientes resultados (ver Tabla 1.):

Para obtener un intervalo de probabilidad del 95 % para la proporción poblacional de hombres consumidores de marihuana se implementará el muestreador Gibbs usando el software R. En particular se asumirá que la a priori para p es una distribución beta(10,50) y que las a priori para λ₁ y λ₂ son normales truncadas en el intervalo (0, 1) con parámetros µ_λ1 = 0,8, 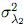= 0,001, µ_λ2 = 0,05 y 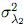= 0,001 (note que esta elección de a prioris para λ₁ y λ₂ es más ventajosa que asumirlas uniformes ya que las normales truncadas modelan de mejor manera estas probabilidades). Por medio de una prueba de estacionaridad se verificó que la cadena de Markov asociada a p converge a la distribución límite (valor-p> 0.1).

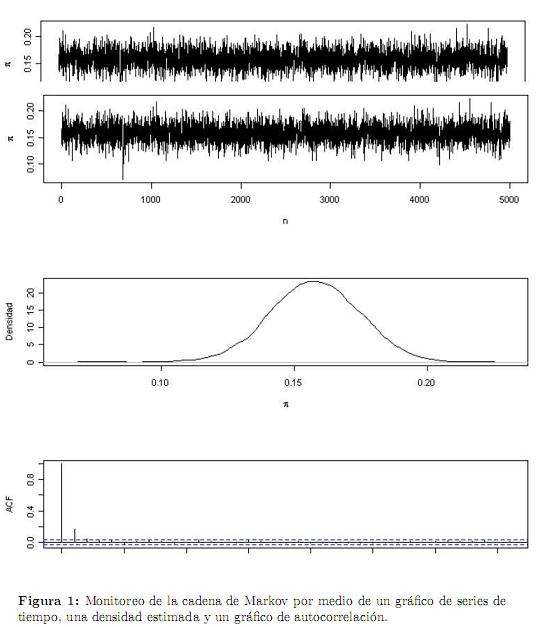
Para monitorear la convergencia, se obtuvieron los gráficos de la cadena, la densidad y el de autocorrelación, que muestran el buen comportamiento de la cadena (Figura 1).

La Tabla 2 muestra el intervalo de probabilidad del 95 % para p y el intervalo de confianza del 95 % para p (basado en el teorema de límite central, . Se observa que este último subestima la proporción poblacional mientras que el primero reporta un rango más amplio debido a la naturaleza del método propuesto que incorpora el nivel de incertidumbre generada por las distintas probabilidades de respuestas falsas.

 

4 Conclusiones

El manejo de la respuesta falsa es un tema complejo entre los investigadores de las ciencias sociales y médicas, muchos de los cuales desconocen como enfrentarlo, ya que técnicas como la respuesta aleatorizada tienen un alcance muy limitado por sus mismas características. En muchas circunstancias, el investigador dispone de información que le permite predecir la fiabilidad de las respuestas a preguntas comprometedoras. Este conocimiento se puede expresar en términos probabilísticos con lo cual se pueden integrar al proceso de estimación de la proporción. En este trabajo, se ha ilustrado como el método bayesiano permite integrar estas incertidumbres en las estimaciones finales en un tema altamente sensible y en el cual los investigadores saben que se presentan respuestas falsas. Uno de los aportes principales es la deducción de la función de verosimilitud la cual es una generalización de aquella propuesta por Winkler y Gaba [13]. El método presentado en este trabajo no se ha discutido en la literatura y por esta razon constituye un aporte original al estado del arte.

 

Agradecimientos

Este trabajo fue realizado con recursos del proyecto de investigación 9201 de la Vicerrectoría de Investigación de la Universidad Nacional de Colombia, código DIME 20101007954. Los autores también agradecen a la Oficina de Bienestar de la Universidad Nacional de Colombia, Sede Medellín por haber proporcionado los datos para ilustrar este trabajo.

 

Referencias

1. SL. Warner. Randomized response: a survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, ISSN 0162-1459, 60(309), 63-69 (1965). Referenciado en 159, 160        [ Links ]

2. SL. Warner. The Linear Randomized Response Model. Journal of the American Statistical Association, ISSN 0162-1459, 66(336), 884-888 (1971). Referenciado en 159        [ Links ]

3. BG. Greenberg, Abdel-Latif A. Abul-Ela, WR. Simmons, DG. Horvitz. The Unrelated Question Randomized Response Model: Theoretical Framework. Journal of the American Statistical Association, ISSN 0162-1459, 64(326), 520-539 (1969). Referenciado en 159        [ Links ]

4. CW. Lamb Jr, DE. Stem Jr. An Empirical Validation of the Randomized Response Technique. Journal of Marketing Research, ISSN: 0022-2437, 15(4), 616-621 (1978). Referenciado en 159        [ Links ]

5. A. Campbell. Randomized Response Technique. Science, ISSN 0036-8075, 236(4805), 1049 (1987). 159        [ Links ]

6. P. Tracy, JA Fox. The Validity of Randomized Response for Sensitive Measurements. American Sociological Review, ISSN 0003-1224, 46(2), 187-200 (1981). Referenciado en 159        [ Links ]

7. JD. Miller. Complexities of the Randomized Response Solution. American Sociological Review, ISSN 0003-1224, 46(6), 928-930 (1981). Referenciado en 159        [ Links ]

8. PD. Bourke, T. Dalenius. Some New Ideas in the Realm of Randomized Inquiries. International Statistical Review / Revue Internationale de Statistique, ISSN 1751-582, 44(2), 219-221 (1976). Referenciado en 159        [ Links ]

9. BG. Greenberg, Abdel-Latif A. Abul-Ela, WR. Simmons, DG. Horvitz. A Multi-Proportions Randomized Response Model. Journal of the American Statistical Association, ISSN 0162-1459, 62(319), 990-1008 (1967). Referenciado en 159        [ Links ]

10. NS. Mangat, R. Singh. An Alternative Randomized Response Procedure. Biometrika, ISSN 0006-3444, 77(2), 439-442 (1990). Referenciado en 159        [ Links ]

11. NS. Mangat. An Improved Randomized Response Strategy. Journal of the Royal Statistical Society. Series B (Methodological), ISSN 1467-9868, 56(1), 93-95 (1994). Referenciado en 159        [ Links ]

12. A. O'Hagan. Bayes Linear Estimators for Randomized Response Models. Journal of the American Statistical Association, ISSN 0162-1459, 82(398), 580-585 (1987). Referenciado en 159        [ Links ]

13. RL. Winkler, A. Gaba. Inference With Imperfect Sampling From Bernoulli Process. in S. Geisser, J. Hodges, S.J. Press and A. Zellner, Eds., Bayesian and Likelihood Methods in Statistics and Econometrics: Essays in Honor of George A. Barnard, Amsterdam, North Holland, ISBN 0444883762, 303-317, 1990. Referenciado en 159, 168        [ Links ]

14. JD. Stamey, JW. Seaman, DM. Young. Bayesian analysis of complementary Poisson rate parameters with data subject to misclassification. Journal of Statistical Planning and Inference, ISSN 0378-3758, 134, 36-48 (2005). Referenciado en 159        [ Links ]

15. DH. Boese, DH. Young, JD. Stamey. Confidence intervals for a binomial parameter base don binary data subject to false-positive misclassification. Computational Statistics & Data Analysis, ISSN 0167-9473, 50, 3369-3385 (2006). Referenciado en 159        [ Links ]

16. SC. Lee, JS. Byun. Bayesian approach to obtain confidence intervals for binomial proportion in a double sampling scheme subject to false-positive misclassification. Journal of the Korean Statistical Society, ISSN 1226-3192, 37, 393-403 (2008). Referenciado en 159        [ Links ]

17. D. Rahardja, YD. Zhao. Bayesian inference of a binomial porportion using one simple misclassified binary data. Model Assisted Statistics and Applications, ISSN 1574-1699, 7(1), 17-22 (2012). Referenciado en 159        [ Links ]

18. A. Gaba. Inferences with an Unknown Noise Level in a Bernoulli Process. Managment Science, ISSN 0025-1909, 39(10), 1227-1237 (1993). Referenciado en 162        [ Links ]

19. G. Casella, Edward I. George. Explaining the Gibbs Sampler. The American Statistician, ISSN 0003-1305 46(3), 167-174 (1992). Referenciado en 165        [ Links ]