Introducción
La comprensión de las fracciones representa un paso clave para el aprendizaje progresivo de las matemáticas (Braithwaite, & Siegler, 2021; Fennell, & Karp, 2017; National Mathematics Advisory Panel, 2008; Torbeyns et al., 2015). Diferentes estudios coinciden en señalar que esta habilidad matemática, correspondiente al nivel primario, es la que más explica el desempeño y aprendizaje posteriores de las matemáticas en el nivel secundario (e.g., Geary et al., 2017; Siegler et al., 2012). Adicionalmente, existe evidencia de que el entrenamiento en la resolución de situaciones problemáticas con fracciones facilita el aprendizaje del álgebra (DeWolf et al., 2016).
La relevancia de las fracciones obedece, entre otros aspectos, a que su aprendizaje exige a los estudiantes revisar la aplicación general de ciertas nociones o reglas que utilizan para el trabajo con números naturales. Por ejemplo, a diferencia de los números naturales, las fracciones que involucran mayor cantidad de dígitos no siempre representan mayor valor (e.g., 1/100 < 1/2); la multiplicación de dos fracciones positivas inferiores a la unidad resulta en un producto menor a ambos factores; las fracciones permiten representar la misma cantidad a través de expresiones equivalentes (e.g., 1/2; 2/4; 50/100), etc. Por estas características, el aprendizaje de las fracciones amplia y profundiza la capacidad de representación y comprensión de las cantidades, y promueve el desarrollo de conocimientos de matemáticas más avanzados (Braithwaite, & Siegler, 2021; Siegler et al., 2011).
Distintos estudios muestran que el aprendizaje de las fracciones resulta difícil para muchos niños, y un porcentaje notorio de ellos sólo incorpora las nociones más básicas de este concepto (Hansen et al., 2017; Jordan et al., 2017; National Center for Education Statistics, 2012; National Mathematics Advisory Panel, 2008; Singh et al., 2021). Identificar los factores que caracterizan y distinguen a los estudiantes que experimentan obstáculos en el aprendizaje de las fracciones, respecto de aquellos que alcanzan una comprensión que se adecúa o supera lo esperable conforme a la instrucción recibida, permitiría planificar y diseñar estrategias didácticas que mejoren el proceso de enseñanza-aprendizaje de éstas. Algunos estudios reportan que el rendimiento en inhibición perceptual (Siegler, & Pyke, 2013), memoria de trabajo (MT) (Bailey et al., 2014; Hansen et al., 2015) e inteligencia fluida (Jordan et al., 2013; Namkung & Fuchs, 2015), predicen el conocimiento de las fracciones; sin embargo, otros no corroboraron estas relaciones (para resultados diferentes en MT ver Jordan et al., 2013, Namkung & Fuchs 2015 y Vukovic et al., 2014; en inteligencia fluida ver Vukovic et al., 2014 y Hansen et al., 2017). La disparidad de resultados puede responder a diferencias metodológicas de los estudios, principalmente respecto a las características de los participantes o al conjunto de predictores incluidos en los modelos explicativos. Estudios de revisión sugieren que el valor explicativo de habilidades cognitivas generales sobre el conocimiento de las matemáticas varía según el nivel de instrucción formal y aprendizaje adquirido (aprendizaje en curso vs. consolidado) (Cragg & Gilmore, 2014; Raghubar et al., 2010; Peng et al., 2016; Stelzer et al., 2019a). Se ha propuesto que, en las etapas iniciales del aprendizaje, la intervención de habilidades cognitivas generales sería mayor, mientras que una vez que los estudiantes han consolidado los conocimientos su intervención se reduciría (Geary et al., 2008). Por otro lado, el aprendizaje de la matemática dependería también de factores específicos del dominio (e.g., conocimiento matemático previo) (Geary et al., 2008), los cuales no han sido controlados de igual forma en todas las investigaciones.
En función de tal estado del arte, el objetivo de este estudio es establecer si las capacidades de inhibición perceptual, MT, inteligencia fluida y división con números naturales caracterizan y diferencian a estudiantes de cuarto año de escolaridad primaria que presenten dificultades en la comprensión de las fracciones, respecto de aquellos que se destacan en tal capacidad. El estudio de estas variables en participantes de este año escolar reviste especial interés, ya que en este se inicia la enseñanza sistemática de las fracciones en el sistema educativo argentino. Las variables discriminantes propuestas han sido seleccionadas ya que, en el caso de la MT y la inteligencia fluida, la literatura presenta resultados diferentes respecto a su contribución a la comprensión de las fracciones cuando ambas son incluidas en los modelos explicativos. Por otro lado, respecto a la inhibición perceptual, no existe evidencia respecto a su contribución al inicio de su enseñanza sistemática. Por último, existe consenso respecto a que las fracciones representan un constructo multifacético que engloba diferentes sentidos, a saber: parte-todo, medida, razón, operador y cociente (Behr et al., 1983; Charalambous & Pitta-Pantazi, 2007). En particular, el sentido de cociente implica entender las fracciones como resultado de una operación de división entre números naturales, por lo que analizar el valor discriminante de este conocimiento previo respecto a habilidades cognitivas generales es de gran relevancia. A continuación, se detalla la evidencia respecto de cada una de las variables discriminantes consideradas en el presente estudio.
Variables discriminantes generales: procesos cognitivos
Inhibición perceptual. La inhibición perceptual constituye un proceso cognitivo que posibilita la focalización de la atención sobre la información ambiental relevante para el logro de metas y suprime la interferencia de los estímulos irrelevantes para tal fin (Diamond, 2013). Diferentes estudios indican que, durante el aprendizaje de las fracciones, los estudiantes tienden a identificar y tratar los componentes de la fracción como números naturales independientes (para una revisión ver Ni, & Zhou, 2005). Por ejemplo, al comparar 1/3 con 1/5, un número notorio de estudiantes concluye erróneamente que 1/5 es mayor porque cinco es mayor que tres. Lo anterior sugiere que la comprensión de los números fraccionarios presentados en formato arábigo (e.g., 4/5) exige inhibir la tendencia a percibir al numerador y denominador como entidades numéricas independientes, y representar la fracción en función de su relación (Siegler & Pyke, 2013).
Algunos estudios señalan que la inhibición perceptual predice la capacidad de cálculo con números fraccionarios en estudiantes de quinto (10-11 años) (Stelzer et al., 2019b) y octavo año (13-14 años) (Siegler & Pyke, 2013); no obstante, su relación al comienzo de la enseñanza sistemática de las fracciones no ha sido analizada. Se espera que la inhibición perceptual facilite la comprensión inicial de las fracciones al suprimir la tendencia a ver las fracciones como dos números naturales independientes y focalizar la atención sobre la relación entre numerador y denominador. Por lo anterior, es posible anticipar que este proceso contribuirá a la discriminación de estudiantes con diferente nivel de comprensión de las fracciones.
Memoria de trabajo. La MT se refiere a un sistema de capacidad limitada responsable de la retención y procesamiento concurrente de la información (Baddeley, 2012). La importancia de la MT para el desempeño académico y aprendizaje general de la matemática ha sido ampliamente documentada (Stefanelli & Alloway, 2018; Canet-Juric et al., 2017; Peng et al., 2016), y algunos autores (Cragg & Gilmore, 2014; Raghubar et al., 2010) han sugerido que las tareas de MT que involucran material verbal (MT verbal) y visoespacial (MT visoespacial) explican en distinto grado diferentes tipos de conocimiento de matemática, según el nivel de aprendizaje de estos.
Las investigaciones que analizan la relación de la MT con el conocimiento de las fracciones son escasas (Peng et al., 2016), consideran únicamente la MT verbal y muestran resultados diferentes respecto de la fuerza de la asociación entre este proceso y el conocimiento de las fracciones, con correlaciones bivariadas entre .10 y .44 (Hansen et al., 2015; Hetch & Vagi, 2010, Jordan et al., 2013; Namkung & Fuchs, 2015). Desde un punto de vista teórico se espera que la capacidad de MT verbal permita distinguir entre estudiantes con diferente nivel de comprensión de las fracciones. La identificación de la magnitud de un número fraccionario exige procesar la relación numérica entre numerador y denominador, lo cual demandaría la representación y procesamiento simultaneo de ambos componentes de la fracción. Por otro lado, las fracciones pueden ser representadas mentalmente como figuras (enteros) fragmentadas en partes iguales, lo que exige retener y procesar mentalmente configuraciones visoespaciales e involucra a la MT visoespacial. Al considerar estas relaciones es posible predecir que tanto la MT verbal como la visoespacial contribuirán a la discriminación de estudiantes con diferente nivel de comprensión de las fracciones.
Inteligencia fluida. La inteligencia fluida es definida como la capacidad de razonamiento abstracto y de resolución de problemas de forma independiente a los conocimientos previos (Cattell, 1971). Esta habilidad se encuentra estrechamente vinculada a la capacidad de MT, ya que el razonamiento abstracto requiere de la retención y procesamiento concurrente de la información; no obstante, la inteligencia fluida representa un constructo más amplio y de nivel superior al de MT que -si bien depende en parte de la capacidad de MT- es parcialmente independiente de la misma (Diamond, 2013; Engle, 2018).
La inteligencia fluida tiene un rol central en el procesamiento y comprensión de información nueva, siendo esencial para la formación y consolidación de nuevos conocimientos y habilidades (Aragón et al., 2013). Tal como fue mencionado, en el sistema educativo de Argentina, la enseñanza sistemática de las fracciones se inicia en cuarto año del nivel primario. La comprensión de las fracciones exige a los estudiantes construir nuevas reglas -diferentes de las que aplicaban en la representación de números naturales- para el trabajo con fracciones (e.g., mayor número de dígitos no siempre representan mayor cantidad) (Braithwaite & Siegler, 2021). En función de lo anterior, se espera que la inteligencia fluida permita distinguir a los estudiantes con diferente grado de comprensión de las fracciones.
Si bien la evidencia empírica actual indica, en general, que la inteligencia fluida predice el conocimiento de las fracciones (Jordan et al., 2013; Namkung & Fuchs, 2015; Stelzer et al., 2021, para resultados diferentes ver Hansen et al., 2017), su valor discriminante respecto de la MT y la inhibición perceptual no ha sido contrastado; por lo anterior en este estudio se analizará dicho valor.
Variables discriminantes específicas del dominio de la matemática
División entre números naturales. Las fracciones representan un constructo complejo que involucra diferentes sentidos. Uno de éstos implica entenderlas como el cociente de una operación de división entre números naturales (a/b) (Charalambous & Pitta-Pantazi, 2007). Algunos estudios indicaron que la capacidad de efectuar operaciones de división entre números naturales predice el conocimiento conceptual de las fracciones en las etapas intermedias de su enseñanza (quinto y sexto año del nivel primario; Hansen et al., 2015; Stelzer et al., 2021); no obstante, su valor discriminante al comienzo de la enseñanza de las fracciones no ha sido explorado. Su estudio es importante para la planificación de la secuencia de contenidos de matemática a desarrollar y las estrategias didácticas que pueden implementarse para la introducción del concepto de fracción. Considerando la relación conceptual entre ambas nociones, se espera que la capacidad de división contribuirá a la discriminación de estudiantes con diferente nivel de comprensión de las fracciones.
Método
Participantes
La muestra fue seleccionada por disponibilidad y estuvo integrada por 175 niños asistentes a cuarto año de la educación primaria de cuatro establecimientos educativos de la ciudad de Mar del Plata, Argentina (tres de gestión pública y uno de gestión privada). Fueron excluidos del análisis de los datos aquellos casos que presentaron alguna de la siguientes condiciones: (a) diagnóstico previo de trastornos neurológicos o psiquiátricos, (b) peso de nacimiento inferior a 2.5 kilos o gestación inferior a las 37 semanas, (d) puntuación en la escala coloreada del Test Matrices Progresivas de Raven (1989) correspondiente con la categoría deficiente (Cayssials, 1993), o (d) se encontraban en etapa de diagnóstico o tratamiento psicológico, psiquiátrico o psicopedagógico.
La muestra final quedó integrada por 135 niños (69 varones y 66 mujeres) de entre 9 y 10 años de edad (M= 9.3; DE=0.42) de diferente estatus social (ES) (18.1% bajo; 32.8 % medio-bajo; 15.5% medio; 20.7% medio-alto; 12.9% alto). No se hallaron diferencias en el conocimiento de las fracciones ni en función del sexo (t (108,89)=-.81, p=.42) o el ES (F(4,89)=1.32, p=.27).
Instrumentos
Ficha Sanitaria. Consiste en un cuestionario de informe paterno que indaga las siguientes variables: (a) meses de gestación alcanzados, (b) peso de nacimiento, (c) diagnóstico de trastornos neurológicos o psiquiátricos previos al desarrollo del estudio, y (d) evaluación diagnóstica o tratamiento psicológico, psiquiátrico o psicopedagógico en curso.
Cuestionario de Estatus Social (ES). Constituye un cuestionario semiestructurado que permite calcular el ES a través de los indicadores nivel educativo y tipo de ocupación del principal sostén económico del participante. Se computó el ES según el Índice de Hollingshead (2011).
Conocimiento conceptual de las fracciones. Se utilizó una prueba de lápiz y papel integrada por 13 ítems que reflejan el modo en el que el conocimiento de fracciones es típicamente evaluado durante cuarto año del nivel primario en el sistema educativo argentino. Un ítem exige representar gráficamente una fracción, cuatro ítems requieren escribir utilizando números arábigos la fracción que se muestra representada en figuras geométricas, cinco ítems exigen comparar y establecer cuál de dos números fraccionarios es mayor; un ítem plantea ordenar cuatro números fraccionarios, y dos ítems representan problemas redactados que requieren utilizar el sentido de la fracción como cociente y relación parte/ todo. Se consideró como indicador general el número de respuestas correctas. La confiablidad estimada a través del alfa de Cronbach fue α =.75.
Capacidad de división. Constituye una adaptación de la tarea de lápiz y papel implementada por Hansen et al. (2015) en estudiantes de quinto año (estudiantes de 10 a 11 años) de Estados Unidos para la medición de este conocimiento. La tarea original presenta seis divisiones (56/8, 42/3, 306/ 9, 91/ 4, 180/60, 1400/400) y requiere que los alumnos resuelvan la mayor cantidad de éstas en 8 minutos. La versión utilizada fue adaptada conforme al nivel de aprendizaje de la división esperado para cuarto año según el sistema educativo argentino (Ministerio de Educación de Argentina, 2011), y muestra las siguientes divisiones: 9/3; 10/4; 56/8; 180/60; 1200/400; 306/9. Se otorgan dos puntos por cada respuesta correcta, y un punto cuando la respuesta es correcta pero se detecta un error en el procedimiento de cálculo. La confiabilidad se estimó a través del coeficiente Alpha de Cronbach (α=.72).
Inteligencia fluida. Se evaluó mediante la Escala Coloreada del Test de Matrices Progresivas (Raven, 1989). Está compuesta por 36 láminas que muestran matrices gráficas con una pieza faltante. Los participantes deben identificar entre seis opciones aquella que completa la matriz. Se consideró cómo indicador el total de respuestas correctas. La confiabilidad en esta muestra fue α=.79.
MT verbal. Se administró la Tarea de memoria de trabajo dual verbal de la Batería de Tareas de Autorregulación Cognitiva (TAC) (Introzzi & Canet Juric, 2012). Constituye una tarea informatizada que evalúa la capacidad de retención y procesamiento concurrente de la información a través de la ejecución de dos tareas, una primaria y otra secundaria. La tarea primaria exige recordar series de dígitos que se presentan, de uno en uno, escritos en diferentes colores. La tarea secundaria requiere que los participantes mencionen en voz alta el color de cada dígito tras su desaparición. El número de dígitos a retener se incrementa de a una unidad tras el recuerdo correcto de la secuencia. La prueba se interrumpe luego de dos errores consecutivos. Se consideró como indicador de la MT verbal la cantidad de dígitos recordados. Esta tarea presenta evidencias de validez convergente y de constructo en niños de 9 a 12 años de Argentina (Canet-Juric et al., 2015; Richard’s et al., 2017; 2020).
MT visoespacial. Se utilizó la Tarea de memoria de trabajo dual visoespacial de la TAC que demanda la realización de una tarea primaria y otra secundaria (Introzzi & Canet Juric, 2012). La tarea primaria exige recordar la secuencia de aparición de cruces de diferentes colores que se presentan, de una en una, sobre una matriz 4x4. La tarea secundaria requiere que los participantes indiquen el color de cada cruz, tocando o señalando con el cursor una paleta de colores colocada a la derecha de la matriz, tras la desaparición de cada cruz. El número de localizaciones a recordar se incrementa de a una unidad tras el recuerdo correcto de la secuencia de localizaciones. Además, la tarea se interrumpe tras dos ensayos sucesivos incorrectos. Se consideró como indicador de la MT visoespacial la cantidad de localizaciones recordadas. Esta tarea presenta evidencias de validez convergente y de constructo en niños de 9 a 12 años de edad de Argentina (Canet-Juric et al., 2015; Richard’s et al., 2017; 2020).
Inhibición perceptual. Se evaluó mediante la Tarea de Búsqueda Visual Conjunta (TBVC) de la TAC (Introzzi & Canet Juric, 2012). En esta tarea el participante debe identificar la presencia o ausencia de un estímulo target (cuadrado azul) que se presenta entre un conjunto de distractores que se caracterizan por compartir una de las dos características visuales que definen el estímulo target: color (círculo azul) o forma (cuadrado rojo). La semejanza visual entre el target y los estímulos distractores produce un efecto de interferencia y demanda la activación de la inhibición perceptual. La tarea está compuesta por tres bloques de evaluación de 40 ensayos cada uno. En cada ensayo el participante debe presionar dos teclas diferentes (Z y M) en función de la presencia o ausencia del estímulo target. En cada bloque, los ensayos se distribuyen en cuatro condiciones definidas por la cantidad de distractores (4, 8, 16 y 32). En cada ensayo el 50% de los distractores son círculos azules y el otro 50% cuadrados rojos. Las condiciones se distribuyen de manera aleatoria por bloque. Se consideró como indicador el porcentaje de respuestas correctas en la condición de 32 distractores (condición de mayor interferencia y mayor exigencia atencional). Esta tarea presenta evidencias de validez convergente, discriminante y de constructo en niños de 9 a 12 años de edad de Argentina (Introzzi et al., 2019; Richard's et al., 2016; 2017; 2020).
Aspectos éticos
Para la realización de este estudio se respetaron los lineamientos éticos definidos por la Asociación Americana de Psicología (APA) y los establecidos en la declaración de Helsinki. Se solicitó a los padres la autorización para que sus hijos participaran a través de la firma de un consentimiento informado. En éste se detallaba el carácter voluntario y gratuito de la participación, los objetivos del estudio y el modo en el que sería implementado. En el caso de los niños se los informó verbalmente del estudio y se evaluó solamente a aquellos que contaban con el consentimiento informado de sus padres y manifestaron su intención de participar.
Procedimiento
Los niños fueron evaluados durante el horario escolar, dentro de los establecimientos educativos a los que asistían, en aulas acondicionadas para tal propósito. Las tareas de MT verbal, MT visoespacial e inhibición perceptual se administraron en una única sesión de evaluación individual. El orden de administración de las tareas fue aleatorizado entre los distintos participantes. Las evaluaciones en inteligencia fluida, división y fracciones se administraron en tres sesiones de evaluación independientes, de forma grupal, en el salón de clases habitual de los estudiantes. Las mismas fueron impartidas por asistentes de investigación entrenados para la administración de tales tareas, los cuales eran ciegos a las hipótesis del estudio. Cada sesión de evaluación tuvo una duración máxima de 40 minutos. Las preguntas sobre ES y la ficha sanitaria fueron enviadas a los padres a través del cuaderno de comunicaciones. Previo a la evaluación de la capacidad de división y fracciones se verificó, a través de una entrevista a los docentes, que los estudiantes habían recibido instrucción y una evaluación escolar de los contenidos que componían cada tarea de matemáticas. La evaluación del conocimiento en fracciones se realizó de forma inmediatamente posterior a la evaluación escolar curricular de dicho contenido.
Resultados
Análisis preliminares
Conformación de grupos de conocimiento de las fracciones. A fin de identificar qué variables caracterizan y distinguen a estudiantes con diferente nivel de comprensión de las fracciones, se establecieron dos grupos que reflejen los niveles extremos en la comprensión de las fracciones: (a) grupo con dificultades en la comprensión (n=35), compuesto por estudiantes con puntuaciones iguales o inferiores a p25 en la tarea de fracciones administrada; y (b) grupo que se destaca en la comprensión (n=39), conformado por estudiantes que presentaban puntuaciones iguales o superiores a p75 en tal tarea. Los participantes restantes (participantes con puntuaciones superiores a p25 o inferiores a p75) no fueron considerados en el posterior análisis de los datos, ya que la meta del estudio fue identificar diferencias entre grupos extremos en el nivel de comprensión.
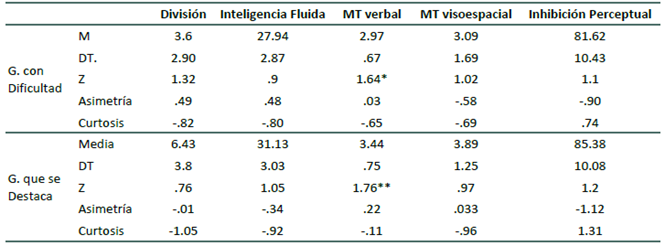
En la Tabla 1 se presentan la puntuación media, desviación típica, valor mínimo, máximo, asimetría, curtosis y el estadístico de Z de Kolmogorov-Smirnov, para cada grupo en las variables de clasificación estudiadas.
Perfil cognitivo de los grupos
A fin de identificar las características que diferencian y permiten predecir la pertenencia de los estudiantes a ambos grupos se efectuó un análisis discriminante. Se verificó el cumplimiento de los supuestos de homogeneidad de varianzas entre los grupos (M de Box = 11,77 p=.77) y la normalidad de las distribuciones de sus puntuaciones según los valores de asimetría, curtosis y el estadístico Kolmogorov-Smirnov (Ver Tabla 1). En el caso de las distribuciones en MT verbal, el estadístico de Kolmogorov-Smirnov indicó que éstas no se ajustaban a la normalidad. No obstante, los valores de asimetría y curtosis no indicaron una desviación notoria de tal distribución, por lo que se consideró que las distribuciones respetaban los supuestos necesarios del análisis discriminante. Los resultados del mismo se presentan en la Tabla 2.
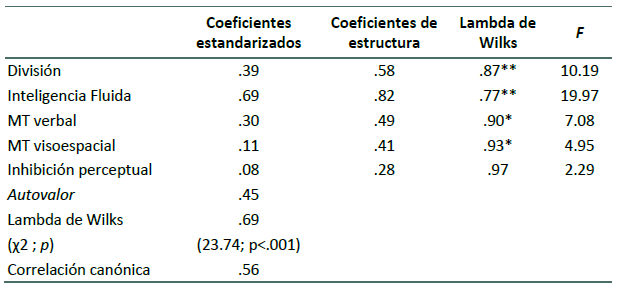
Tal como se observa en la Tabla 2, la función Lambda de Wilks para los distintos factores cognitivos indicó que - a excepción de la inhibición perceptual- las medias de los distintos factores cognitivos presentan diferencias significativas en los grupos de conocimiento de las fracciones. La función canónica discriminante indicó que la función lineal discrimina adecuadamente, ya que presenta un autovalor de .45 y una correlación canónica de .56 (el 56%) en los grupos de conocimiento bajo y alto.
Las funciones discriminantes canónicas no tipificadas evaluadas en los centroides de los grupos mostraron una clara discriminación con valores de -.73 para el grupo de conocimiento bajo y de .61 para el grupo de conocimiento alto. Las medidas con más peso para predecir el grupo de pertenencia fueron: inteligencia fluida, capacidad de división y MT verbal (ver Tabla 2). Los resultados de la clasificación obtenida para la estimación de la pertenencia a un grupo o a otro, indicaron que el 70.6% los casos agrupados originales fueron clasificados correctamente; de éstos 64.5% de verdaderos positivos fueron para el grupo de conocimiento bajo y 75.7% para el grupo de conocimiento alto.
Discusión
El objetivo de este estudio fue establecer si las capacidades de inhibición perceptual, MT, inteligencia fluida y división con números naturales caracterizan y distinguen a los estudiantes de cuarto año que presentan diferente nivel de comprensión de las fracciones. La función discriminante permitió clasificar correctamente al 70.6% de los casos, e indicó que los estudiantes que muestran diferente nivel de comprensión de las fracciones se caracterizan por presentar rendimientos diferenciales en las capacidades de MT verbal, MT visoespacial, inteligencia fluida y división. De estos factores, la inteligencia fluida, la MT verbal y la capacidad de división presentaron mayor peso en la discriminación entre grupos.
Estudios previos señalan que la inteligencia fluida se relaciona con el conocimiento conceptual de las fracciones (e.g., Jordan et al., 2013; Namkung & Fuchs, 2016), no obstante, su valor discriminante respecto de los factores cognitivos abordados en este trabajo no había sido contrastado. Los resultados del presente estudio indican que la inteligencia fluida constituye la habilidad de mayor peso en la caracterización y discriminación de los grupos de estudiantes en función del nivel de conocimiento conceptual de las fracciones: con dificultades y con facilidades en la comprensión de las fracciones. Esto podría explicarse por el hecho de que la comprensión de las fracciones exige a los estudiantes construir e integrar diferentes significados de las mismas (Charalambous & Pitta-Pantazi, 2007; Fennell, & Karp, 2017; Lortie-Forgues et al., 2015), lo cual demandaría a la operación básica de razonamiento relacional implicada en la inteligencia fluida (Jastrzębski et al., 2020). En cuarto año del sistema educativo de Argentina se abordan los siguientes sentidos de las fracciones: (a) relación parte-todo, esto es la relación de un entero con un número de partes iguales en las cuales éste se divide; (b) cociente, es decir, el resultado de una operación de reparto y, (c) medición, esto es, un modo de representación de cantidades (Ministerio de Educación, Ciencia y Tecnología de la Nación, 2007). El razonamiento relacional es la capacidad de considerar relaciones entre representaciones mentales individuales (relaciones de primer orden) y entre conjuntos de representaciones mentales que se encuentran asociadas entre sí (relaciones de segundo orden) (Jastrzębski et al., 2020; Singley & Bunge, 2014). La construcción de los diferentes sentidos de las fracciones exige establecer relaciones de primer y segundo orden. Por ejemplo, para comprender la cantidad representada en un número fraccionario, los estudiantes deben establecer relaciones de primer orden entre el numerador y el denominador. Asimismo, para comparar dos fracciones los estudiantes deben establecer relaciones de segundo orden, ya que deben determinar el grado en que la relación entre el numerador y denominador de una fracción difiere de la relación existente entre el numerador y denominador de la otra fracción (Singley & Bunge, 2014). Sumado a lo anterior, el razonamiento relacional permite identificar las correspondencias entre los diferentes sentidos del concepto fracción. Por ejemplo, posibilita a los estudiantes reconocer la relación entre los hechos de que: (a) el número ½ se ubica en la mitad de una recta numérica de 0 a 1 (sentido de medición); (b) para comprar 1 kilos de arroz envasado en paquetes de ½ kilo se deben comprar 2 paquetes (sentido parte-todo), y (c) si se debe repartir en partes iguales un chocolate entre dos amigos, cada uno recibirá ½ del mismo (sentido de cociente). En todas las situaciones planteadas la fracción “½” cobra diferentes sentidos, el razonamiento relacional permitiría reconocer las correspondencias entre los diferentes usos y sentidos de esta fracción, contribuyendo a la comprensión general del concepto.
De forma complementaria a la explicación anterior, el modo de enseñanza de las fracciones en el sistema educativo argentino requiere que los estudiantes utilicen su capacidad de razonamiento relacional. Puntualmente, el enfoque didáctico sugerido desde organismos gubernamentales propone que los estudiantes resuelvan situaciones problemáticas que les permitan luego comparar y contrastar las diferentes estrategias y/o resultados. La operación de razonamiento relacional intervendría en la construcción e integración de los diferentes sentidos de las fracciones al posibilitar: (a) la comparación entre diferentes estrategias y/o resultados (e.g., los estudiantes deben armar 3 kilos y medio de azúcar a partir de paquetes de ¼; ½ y 1 kilo de azúcar; luego se comparan las respuestas ofrecidas por cada estudiante para establecer cuál sería la forma correcta y que implicaría llevar menos paquetes de azúcar); (b) la identificación de relaciones entre diferentes situaciones problemáticas que permitan la construcción conceptual de las fracciones (e.g., conforme al ejemplo anterior: “Felipe compró 3 kilos de yerba con paquetes de ½ kilo. Juan compró la misma cantidad con paquetes de ¼ y Malena con paquetes de 1 kilo. ¿Será cierto que Felipe tiene el doble de paquetes de yerba que Malena? ¿Será cierto que Malena tiene la mitad de paquetes que Juan?, ¿Cómo te diste cuenta?”); y (c) el establecimiento de relaciones entre diferentes aspectos dentro de situaciones problemáticas que trabajen diferentes sentidos del concepto (e.g., en el problema: “Para la escuela Juan tiene que leer un apunte de 10 páginas. Decidió leer todos los días la misma cantidad de páginas para en 4 días poder terminarlo. La mamá dice que debe leer ¼ del libro todos los días y Juan dice que tiene que leer 2 páginas y media por día. ¿Es correcto lo que dice su mamá? ¿Y lo que dice Juan?”, se trabajarían los sentidos de cociente y parte-todo). La capacidad de razonamiento relacional intervendría en la identificación e integración de las relaciones entre estos sentidos.
Las anteriores interpretaciones conllevan importantes implicaciones prácticas. El empleo de fracciones de uso frecuente (e.g., ¼; ½) en problemas formulados en el marco de situaciones cotidianas (e.g., compra de productos), podría facilitar la identificación de relaciones de primer orden entre los componentes de la fracción. Una vez que las mismas son comprendidas por los estudiantes, podría avanzarse en el trabajo con fracciones de uso menos frecuente y en la identificación de relaciones de segundo orden (e.g., en una recta numérica de 0 a 2, donde se muestra la fracción ¼ solicitar a los estudiantes colocar la fracción “5/4”). Respecto de este último aspecto, la cantidad de relaciones de segundo orden que los estudiantes deben establecer debería ser ajustada según su nivel de comprensión. En este sentido, el establecimiento de relaciones de segundo orden exige que las relaciones de primer orden que subyacen a éstas sean conocidas por los estudiantes (Richland et al., 2017). Por último, definir el número de estrategias de solución a comparar conforme al nivel de conocimiento de los estudiantes, también podría beneficiar a los que tienen menor inteligencia fluida.
Por otro lado, el valor discriminante de la MT verbal puede explicarse al considerar que la representación de la magnitud de una fracción exige considerar la relación numérica entre numerador y denominador, es decir, representar y procesar de modo simultáneo ambos componentes de la fracción. Seleccionar, para la enseñanza inicial de las fracciones, actividades con menor exigencia de los recursos de la MT verbal podría facilitar la adquisición de este conocimiento. Por ejemplo, las actividades que proponen la identificación y/o representación gráfica de las fracciones presentan menor exigencia de MT verbal respecto de aquellas actividades en las que tanto el formato de presentación del problema como el de la respuesta solicitada son de carácter verbal. Además, la utilización de materiales manipulativos para la resolución de problemas también reduciría la carga de MT, y facilitaría la comprensión inicial del concepto de fracción. Por ejemplo, Rejeki, Setyaningsih, y Toyib (2017) indicaron que el uso de actividades didácticas con bloques de construcción tipo Lego facilita el aprendizaje conceptual de las fracciones (Rejeki et al., 2017).
Respecto del valor de la MT visoespacial en la diferenciación entre grupos, podría explicarse teniendo en cuenta que este proceso posibilita la retención y procesamiento mental de información visoespacial. En este sentido, la MT visoespacial permitiría la representación mental de las fracciones como configuraciones visuales fragmentadas, y la utilización de este formato representacional para la solución de problemas con fracciones. Se ha sugerido que la resolución de problemas favorece la construcción y comprensión de los diferentes sentidos de la fracción (Parra & Saiz, 1994). Es posible que la representación mental de las fracciones como figuras fragmentadas, facilite la resolución de problemas y, consecuentemente, la comprensión de las fracciones. Futuros trabajos podrían analizar si el modo de representación de las fracciones utilizado para la resolución de problemas modera el efecto de la MT sobre el nivel de conocimiento de las fracciones alcanzado.
Por otra parte, los resultados del presente estudio indican que los niños con menor conocimiento conceptual de las fracciones se caracterizan y distinguen respecto de aquellos que se destacan en la comprensión de este conocimiento en su capacidad de división. Esto puede originarse en la relación conceptual entre la operación de división y el concepto de fracción. Las fracciones son esencialmente una forma de división (a/b), y la comprensión del concepto de fracción involucra su representación como un cociente producto de una operación de reparto (Charalambous & Pitta-Pantazi, 2007). Reforzar la comprensión de la operación de división con números naturales previo a la enseñanza de las fracciones podría beneficiar el aprendizaje conceptual de las mismas.
Por último, si bien se esperaba que los estudiantes con distinto nivel de comprensión de las fracciones se diferencien entre sí en su capacidad de inhibición perceptual, este proceso no contribuyó a dicha discriminación. La inhibición perceptual implica la capacidad de impedir el acceso al foco atencional de la MT de aquella información que es irrelevante para el logro de metas (Diamond, 2013). Debido a que distintos estudios han indicado que los estudiantes muestran un sesgo hacia la representación de los componentes de la fracción como números naturales independientes (Ni & Zou, 2005), se esperaba que la inhibición perceptual contribuyera a la discriminación entre ambos grupos de estudiantes; sin embargo, esta hipótesis no se vio sustentada por los datos. Es posible que el sesgo hacia la representación y uso de las fracciones como números naturales independientes, se origine en la dificultad de inhibir las representaciones mentales numéricas de cada componente de la fracción que se activan en la MT producto de la percepción de un número fraccionario. De este modo, el proceso inhibitorio no intervendría a nivel de la percepción, sino a nivel de los contenidos de la MT que se encuentran en un estado de mayor activación. Algunos estudios sugirieron que la supresión de la información a nivel de la percepción (designada inhibición perceptual) es independiente de la capacidad de inhibición a nivel de las representaciones mentales activas en la MT (denominada inhibición cognitiva) (Diamond, 2013; Miyake & Friedmman, 2004). Es posible que la inhibición cognitiva - y no la inhibición perceptual- explique el sesgo observado en distintos estudios en la representación de las fracciones. En futuros estudios podría analizarse el valor discriminante de la inhibición cognitiva a fin de mejorar la caracterización e identificación de niños con diferente nivel de conocimiento conceptual de las fracciones.
Es importante mencionar como limitación de este estudio que el número de participantes en cada grupo del conocimiento de las fracciones es reducido. Lo anterior restringe la generalización de los resultados. No obstante, los datos aportados constituyen una primera aproximación para la identificación de los factores cognitivos y conocimientos matemáticos que caracterizan y distinguen a los estudiantes que alcanzan diferente nivel del conocimiento de las fracciones. Conocer los factores que caracterizan y distinguen a los mismos en la etapa inicial de su enseñanza es importante para diseñar estrategias que faciliten la construcción de este conocimiento a lo largo de la escolaridad. Con este trabajo se aspiró a contribuir a tal meta. Una serie de interrogantes quedan planteados para futuros trabajos. Por ejemplo, los factores cognitivos identificados en este estudio ¿continuarán caracterizando y diferenciando a los grupos de estudiantes con diferente nivel de conocimiento de las fracciones en etapas posteriores de la enseñanza? ¿el modo de representación de las fracciones utilizado en la resolución de problemas modera el efecto de los procesos y habilidades cognitivas sobre el aprendizaje de las fracciones? ¿la inhibición cognitiva opera como un factor discriminante entre estudiantes que alcanzan diferente nivel de conocimiento de las fracciones? La repuesta a éstos permitirá profundizar el conocimiento de los factores cognitivos asociados a este conocimiento.