Introducción

En los actuales tiempos de incertidumbre, emergentes particulares, complejidades y realidades fluctuantes que demandan a la educación en general y al profesor en particular (Ortega, 2019; Allaud, 2009) hablar del quehacer docente conlleva mencionar su vinculación con la dualidad reflexión-práctica, en la que la sinergia y la reciprocidad son relevantes (^{Domingo y Gómez, 2014}) . Reflexión que hace la diferencia a la hora de enfrentar proactivamente los desafíos y hacer del ejercicio docente un saber superior en crecimiento y evolución (^{Schön, 1987}); o bien, lo que para ^{Perrenoud (2004)} supone una postura, una forma de identidad o un habitus. Reflexión, que si bien juega un rol protagónico en el mejoramiento y fortalecimiento del docente, su desarrollo es progresivo y en abierta vinculación con las experiencias, realidades, saberes y situaciones que se enfrentan.

En consecuencia, la formación profesional de un docente es un proceso continuo y permanente, mediante el cual se espera que un estudiante desarrolle las capacidades necesarias para afrontar los desafíos de enseñar en una sociedad basada en el conocimiento (^{Hargreaves, 2003}). La etapa de formación inicial docente (FID) constituye un periodo clave en el desarrollo de habilidades y destrezas, transitando desde la propia experiencia escolar o etapa experiencial pre profesional a la realidad de la profesión docente (^{Marcelo y Vaillant, 2009}). Para ^{Fernández-Cruz (2010)}, la etapa escolar suele marcar tendencias, creencias y formas de ver lo que hace, cómo lo hace y cuál es el ser y hacer de un docente. Para tal efecto, el modelaje preprofesional y las experiencias vividas en la etapa de socialización profesional (^{Knowles, 2004}; Marcelo y Vaillant, 2009) son claves para contextualizar y proyectar estrategias tanto en lo personal como en lo profesional.

En consecuencia, la FID responde a la integración de aspectos personales y profesionales en un escenario de aprendizajes multidimensionales (^{Haas, 2017}; Correa, 2010), que deben plasmarse en una identidad y perfil de buen profesor. ^{Kaasila (2007)} establece que el análisis de la manera en que los maestros en formación hablan sobre sus vivencias durante sus propias experiencias escolares ayuda a comprender sus propósitos, motivos y acciones. De allí que se releven como hitos de partida para proyectar nuevos y más significativos aprendizajes. Es decir, las personas aprenden producto de la reflexión sobre sus concepciones y experiencias previas, ya que el conocimiento profesional y las prácticas de los profesores están profundamente enraizados con las experiencias individuales de sus profesores del pasado y con los objetivos del futuro.

Reflexión

Desde el paradigma reflexivo de la formación, que en términos de Schön (1998) enfatiza la profesionalización docente, se concibe a la reflexión como una alternativa formativa, centrada en la persona, "rescatando la experiencia personal y profesional para la actualización y mejora de la tarea docente" (^{Domingo y Anijovich, 2017}, p. 34). La misma que opera como caja de resonancia en la que el pensamiento, creencia, experiencia que ingresa se transforma y evoluciona en aprendizaje y crecimiento. Lo que permite al docente (en formación, principiante o formado) desarrollar nuevas ideas, un conocimiento propio, único, particular, que constituye sus repertorios de actuación profesional y referencias para superar lo técnico, para encontrar respuestas a la incertidumbre (^{Alliaud, 2017}). De allí que el profesor tome conciencia de sí mismo asumiendo el rol de docente y las funciones que emanan de este: aprender-comunicar-enseñar desde la práctica reflexiva (Ortega, 2019).

Activadores de la reflexión

^{Domingo y Gómez (2014)} plantean que la reflexión puede ser activada por un elemento cognitivo, relativo a los saberes propios de un buen docente; un elemento crítico, vinculado a aspecto ético, social y/o valóricos del quehacer educativo y el narrativo, asociado a los diversos relatos de un docente, como se muestra a continuación.

Fuente: Elaboración propia

Esquema 1 Activadores de la reflexión 

A partir del esquema anterior, en esta investigación el foco está puesto en el último activador narrativo, particularmente la autobiografía como una narración del docente en formación, en la que va rememorando espacios vividos en su etapa de estudiante, aportando valiosa información para comprender la realidad del maestro, estimulando la práctica reflexiva (^{Brubacher, Caser y Reagan, 2000}) y cuyas aplicaciones son multidimensionales (^{Domingo y Gómez, 2014}).

Metodología

Esta investigación es de carácter cualitativo, sobre dos estudios de casos a través del desarrollo de una autobiografía matemática como un punto de partida para la reflexión. La autobiografía matemática corresponde a la descripción de experiencias en dicha área y permite caracterizar a la persona matemáticamente. Es considerada como una herramienta efectiva para contar historias sobre uno mismo como un aprendiz de matemática y, a la vez, como futuro profesor o profesor en formación (^{Wilson & Latterell, 2017}). ^{Lipovec y Antolin (2014)} sostienen que en las autobiografías matemáticas los profesores en servicio escriben sobre las experiencias pasadas y presentes que consideran significativas para su futuro como profesores de esta área. Especialidad que suele despertar grandes aprehensiones en los estudiantes.

La elección de los participantes fue realizada de manera aleatoria y por disposición voluntaria dentro de un grupo de 218 estudiantes de la carrera de Pedagogía de Educación Básica (Primaria) de la Pontificia Universidad Católica de Valparaíso. Para este estudio, con base en la información entregada y las expectativas de su contenido informativo (^{Flyvbjerg, 2006}), se seleccionaron dos de cuatro casos realizados en el marco de las mejoras para la formación docente en este nivel.

En particular se opta por aquellos casos que presentan la máxima variación entre los puntos de inflexión, a fin de obtener, a partir de estos, información acerca de la importancia de las circunstancias del proceso, resultados de aprendizaje y experiencias en matemática. Así, el análisis se centra en detectar los puntos de inflexión que han vivido los informantes, para luego presentar sugerencias o alternativas de acción en la formación docente. Por lo anterior, se consideró una parte escrita, una gráfica y una oral. Igualmente, para apoyar la autobiografía se diseñó un documento con cuatro partes: (1) datos personales, (2) sección sobre los recuerdos, percepciones y sentimientos asociados a la matemática, (3) sección sobre las experiencias en matemáticas, en la cual se debían completar un gráfico y describir estas experiencias y (4) sección sobre la autoefi-cacia en matemática, la cual también contenía un gráfico (figura 1) para visualizar la percepción personal sobre la autoeficacia a través de los años.

La representación gráfica de la biografía matemática individual del aprendizaje (^{Reitz-Koncebovski, Goral & Kortenkamp, 2018}) permite visualizar los puntos altos y bajos de la biografía matemática de una persona. En el eje horizontal se ha considerado la edad de la persona y en el eje vertical la valoración de la experiencia, que va de -10 a 10 (figura 1). Con esto se espera que la persona pueda describir la situación vivida, utilizando una escala personal que permita decidir rápidamente si la situación fue de éxito 10, de logro mediano alrededor de 5, situación neutra en el cero y situaciones de fracaso en el -5 y de fracaso rotundo en -10.

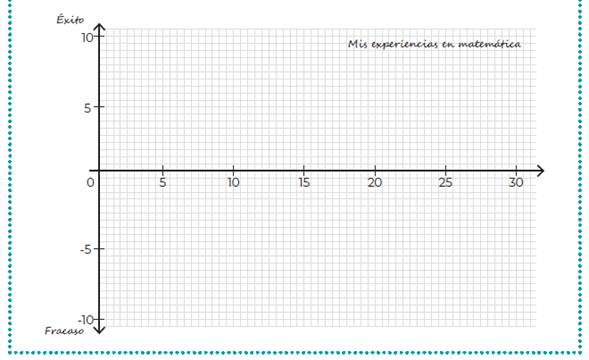
Fuente: Elaboración propia

Figura 1 Plano cartesiano para valorar las experiencias personales en matemática a través de los años 0 a 30 

En la figura 1 se muestra el plano cartesiano correspondiente a las experiencias en matemática de las participantes para representar las valoraciones de sus experiencias según la edad. En el eje X, la edad llega hasta los 30 años, rango etario de los informantes. En el eje Y, van las valoraciones personales, que pueden ir de -10 a 10. Los profesores en formación recibieron dos planos para elaborar gráficos: uno correspondiente a las experiencias en matemática y otro vinculado a la autoeficacia en matemática. Los datos obtenidos fueron tabulados y traspasados al programa "numbers" para generar un solo gráfico con dos curvas. En ellos es posible visualizar de manera efectiva cuáles son los puntos de cambio desde una situación valorada positivamente a una situación valorada negativa, o viceversa. A estos puntos, como se adelantó, se los ha denominado puntos de inflexión.

La entrevista semiestructurada se desarrolla con base en lo que se visualiza en el gráfico y lo que han escrito previamente sobre ellos. Para el análisis de las autobiografías matemáticas se ha considerado una visión holística de los casos; es decir, se le analiza como un todo y cada parte del texto es interpretada en el contexto de las otras partes.

Para ^{Gellert (2001)} y ^{Kaasila (2007)}, las entrevistas semiestructuradas tienen como propósito estimular al entrevistado para que exprese lo que piensa y siente acerca de las matemáticas. La entrevista semiestructurada permite profundizar en cada caso sobre los momentos, se solicita a los participantes que describan este momento; para continuar se consideraron algunas de las siguientes preguntas orientadoras:

Resultados

Cada caso es presentado de forma holística. Al inicio, los recuerdos asociados a la matemática, correspondientes a la parte escrita de la autobiografía. Luego se muestran los gráficos realizados por las estudiantes y finalmente se presentan extractos de la entrevista realizada en cada caso. Para organizar la presentación de los resultados se considera un nombre ficticio y se dan algunas consideraciones generales de cada estudiante.

Caso 1: Fabiola, 24 años, estudios anteriores en Pedagogía en Matemática para el nivel secundario, tiene 3 años como estudiante en la carrera de Pedagogía para primaria. La entrevista duró aproximadamente 20 minutos.

En relación con los recuerdos, percepciones y sentimientos con los que asocia la palabra "matemáticas", Fabiola señaló:

Lo asocio a algo que puedo entender con mayor facilidad, dado que, según yo, es algo mecánico. Para mí, las matemáticas son divertidas porque, como dicen, es todo lo que nos rodea. Actualmente, las matemáticas en la universidad, para mí, no han sido algo emocionante, pero eso no quiere decir que me dejen de gustar, a pesar del tipo de calificaciones que me entregan.

La visión de Fabiola se asocia con una baja complejidad, con una matemática que es, más bien, repetitiva y mecánica. Esto revela una posible fijación en los algoritmos, más que en la resolución de problemas o en los desafíos que requieren de mayores niveles de análisis, reflexión o resolución. Igualmente, alude a una relación entre lo divertido de la matemática y su vinculación con lo real. Podríamos decir que esta conexión es positiva y que le resulta fácil, simple a nivel escolar. No así a nivel universitario, ya que reconoce que no han sido, a este nivel, emocionantes pero que le siguen gustando a pesar de sus malas calificaciones, priorizando una sensación a un resultado o rendimiento.

En cuanto a los gráficos de su autobiografía, la valoración de sus experiencias, junto a su autoeficacia, se puede apreciar en la figura 1 que todas ellas se encuentran en un nivel positivo (entre 3 y 7) y muy positivo (superiores a 7). Lo mismo ocurre con su autoeficacia en matemática: su autovaloración se encuentra sobre el nivel 5, a partir de los 5 años, manteniéndose sobre 6 a nivel de su vida. En este gráfico se aprecian 4 puntos de inflexión durante su vida. El primero como a los 12 años; el segundo, a los 15 años; el tercero, a los 18 años, y el cuarto sobre los 20 años.

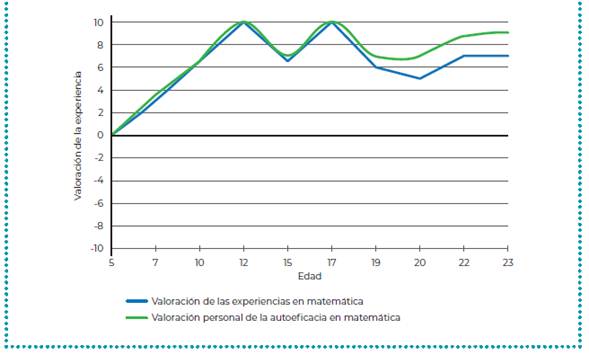
Fuente: Elaboración propia

Figura 2 Representación gráfica de la valoración personal de Fabiola para sus experiencias y autoeficacia en matemática 

En la figura 2 se aprecia que desde los 7 a los 12 años sus experiencias estuvieron en los niveles 3 a 10 de éxito y bajaron entre los 12 a 15 años. Subieron nuevamente en los últimos años de enseñanza secundaria, entre los 7 a 10 en nivel de éxito, y se mantuvieron en los niveles 6 y 7 de éxito de los 19 a 24 años. Es decir, sus experiencias fueron bastante positivas, y continúan así a nivel universitario. En cuanto a la visión general de Fabiola sobre su autobiografía matemática, expresó:

Mi experiencia en matemáticas ha sido grata dado que para mí es fácil comprenderlas, pero esto no quiere decir que las personas que me enseñaron fueran buenos profesores. Muchas veces tuve que buscar las formas de aprender, ya sea por internet, un libro o que un compañero me explique.

Esto confirma su cercanía con la matemática y que posee ciertas habilidades para entenderlas y estudiar sola. Además, relaciona la forma de enseñar con sus propios logros y necesidades de apoyo externo.

En cuanto a la autobiografía sobre su autoeficacia, en la figura 2 se observa similitud entre la curva de autopercepción y experiencias, lo cual indica una relación fuerte entre lo vivido y su autopercepción sobre sus capacidades en matemática.

En cuanto a la visión general de Fabiola sobre su autopercepción, precisó:

Si bien es algo que no me cuesta aprender, no estudio constantemente esta disciplina, ya sea por poca motivación o porque me organizo los tiempos. Por lo general, solo coloco atención en clases y hago las guías cuando se debe, pero no por cuenta propia. En palabras mas simples, estudio para la prueba más que nada.

Fabiola relaciona las matemáticas como algo fácil para ella, indicando que los buenos resultados dependen de atender en clases y desarrollar sus guías. Finalmente, comentó que solo le interesaba aprobar el curso.

La entrevista se centra en los puntos de inflexión de Fabiola. Primero, el que ocurre al pasar de la básica a la media, de los 12 a los 15 años, donde reconoce que sus experiencias en matemática eran muy mecánicas, pero exitosas. En el primer extracto Fabiola describió este punto de inflexión:

dadas las clases tradicionales que tenía... me enseñaban en la pizarra, nunca era algo concreto, pasaba a ser solo pictórico o simbólico... ¡ahhhh! entonces hago lo de la pizarra, hago el ejercicio y se acabó. Manteniendo ese constante ejercicio en la sala, nunca me fue mal.

En este extracto reconoce debilidades en clases tradicionales que difieren de lo aprendido en la universidad. Agrega términos específicos de la especialidad, como son lo concreto, pictórico y simbólico. Reconoce que lo simbólico es fácil y que tiene logros académicos.

En el siguiente extracto, Fabiola se encuentra en secundaria y se enfrenta a un conocimiento que le resultó más complejo y del cual no recibe retroalimentación:

El profe decía haz la guía y estás bien. El tema era ecuaciones, eran ecuaciones grandes; el profesor insistía en que sí es o que no es para la PSU, para la PSU¹ (enfatiza el tono de importancia), era lo más importante. Entonces las hacía no más [las guías]. Y me equivocaba en cosas tan chicas y el profe no me decía si estaba bien o mal. Entonces yo dije: 'ya, voy a estudiar, no más'. Antes tenía promedio 6,3 y 7. Ahora 5,3².

Se muestra que sus resultados ya no son los mismos, aunado a molestia con el docente por la falta de retroalimentación del trabajo y priorizar una prueba estandarizada por sobre el propio aprendizaje. Prueba que para ello era irrelevante.

Se evidencia en la narrativa un proceso autorreflexivo y analítico, mediante la pregunta y respuesta que se plantea sobre este punto de inflexión, como señala:

¿Qué estoy haciendo? ... ya no estoy estudiando lo suficiente ... ya, empecé a subir de a poquito y me costó eso del profe de básica al profe de media.

Con esta pregunta asume una actitud proactiva y logra revertir la situación, cambiando el punto de inflexión y ocupándose de mejorar la situación. Fabiola reflexiona y decide que debe estudiar más para mejorar sus resultados, en concordancia con la visión tradicionalista que valida la mecánica para enseñar y el estudio para aprender con buenas calificaciones.

Sobre los elementos que gatillarían este punto de inflexión alude el cambio de estilo de enseñanza, la no retroalimentación, la complejidad de la temática y una condicionante relacionada con la preparación a la prueba de selección universitaria, que además inciden en su motivación.

acá el profesor de media no retroalimentaba mucho, no había una cosa de ya pues chiquillos [como de animar y motivar].

Ante los dichos de la informante, se le preguntó por qué consideraba que la forma de mejorar era estudiando más.

Siempre me gustó las Matemáticas, es un lenguaje fácil, una cosa que yo podía hacer, los números se mueven [para allá, para acá], no era algo difícil para mí. Entonces, como que me frustraba un poco de por qué me está costando tanto. Después, con los años, me fui dando cuenta, no es que me haya dado cuenta al tiro [inmediatamente].

Entre los factores externos menciona su desvinculación con la realidad, con las motivaciones etarias, además de priorizar resultados estandarizados, una visión academicista y orientada hacia el ingreso de sus estudiantes a la universidad en desmedro de la falta de oportunidades para compartir experiencias de aprendizajes. Precisó:

Yo me acuerdo que el liceo tenía esa mentalidad de PSU, entonces cuando a uno le iba más o menos, era como pucha [expresión de incomodidad], [tienes] que esforzarte más... no había grupo de estudio, en esa etapa, también estaba en la adolescencia. Uno se preocupa por otras cosas.

En este caso, a la estudiante le gusta, las matemáticas y le va bien con ellas, relaciona sus buenos resultados con experiencias positivas. Igualmente, releva los grupos de estudios y que en la adolescencia se priorizan otros temas:

Los adolescentes están pendientes de otras cosas, de pintarse, de hablar con el otro, no están ni ahí con una guía. Yo también estaba en esa etapa de que quería pintarme, hablar con niños, quería ir al recreo.. ¿de qué me servía llegar a la sala y ver una guía?... me decía, pucha que fome, es como nada, no había como un diálogo, no había ejemplos de compra de maquillajes, no había ninguna cosa real, solo todo abstracto, por eso me empezó a ir mal, además que el profe era fome."

Se refleja que el desinterés por la clase y la forma de enseñar matemática del profesor(a) desanima completamente a Fabiola por estudiar. Primero, reconoce que en la adolescencia cambian las prioridades. Segundo, la matemática se presentaba desvinculada de su realidad e intereses, impidiendo el diálogo y la conexión. Fabiola sugiere ejercicios de compras de maquillaje para darle sentido.

Respecto a la expresión "el profe era fome", se le pide profundice en esa percepción:

Es que solo hablaba de lo simbólico, o sea, hablando en términos pedagógicos; el profesor no pasaba a la parte pictórica o a la concreta, era todo simbólico, entonces era abstracto, ya se entiende en la pizarra, pero mis compañeros no tomaban en cuenta al profesor. luego uno empieza a tomarle el peso.

Aquí reflexiona sobre que hay elementos de la didáctica de la matemática que se omitieron en su periodo de aprendizaje, y precisa que lo concreto y lo pictórico pudieron haber hecho una diferencia en sus resultados de aprendizaje y en la forma de acercarse al objeto de estudio. Agrega que lo simbólico se puede entender en la pizarra y que los compañeros no atendían al profesor, con lo cual da luces sobre los desafíos que se enfrentan en la enseñanza en secundaria. Al final indica que luego se empieza a tomar el peso. Respecto a lo cual se le consulta si es el peso, el gusto o ambos lo que se debería considerar. A lo que respondió:

Es que el gusto siempre estuvo, siempre me han gustado las matemáticas, igual en la universidad, a mí me gustan, yo estudio para las pruebas y me va bien, si me saco un siete o un cinco, me da igual, me siguen gustando, el tema es: si la persona me motiva, yo voy a dar mi 100 %, aunque esto es súper criticable, pero no me motiva seguir haciendo más para ese ramo.

Con ello enfatiza que su gusto por la matemática siempre ha estado, y nos da una clave sustancial en su forma de enfrentarse a las pruebas, indicando que le da igual el resultado, pues le gustarán de todas maneras. Indica que este depende de la motivación que le dé el profesor de turno; si está motivada, entregará todo y, por lo tanto, tendrá mejores resultados.

De esta forma, se finaliza el primer punto de inflexión y se retoma el gráfico para que Fabiola explique la relación que visualiza entre sus buenas notas (capacidad en matemática) y sus recuerdos positivos en ella. Respecto a lo cual indicó que los profesores la querían mucho por tener buenas notas.

Se hizo un resumen de la entrevista y se pasó al siguiente punto de inflexión, contextualizado entre el último año escolar y el ingreso a la universidad. Así describe Fabiola el punto de inflexión:

aquí [indicando el punto del gráfico] estaba en cuarto medio [último año del colegio] y me iba bien, porque estaba en el matemático., pero después yo entré a estudiar pedagogía en matemática³. No me gustaba como enseñaban y me pasó lo mismo que en primero medio. No perdía el gusto por la matemática, lo que me cargaba era ir a aprenderlas, era como por qué me enseñan así.. , yo prefería a veces estar en la casa, no me enseñaban, no sentía,. no me transmitían ese amor, que yo pensaba que iba a pasar.

Al ingresar a la carrera de Pedagogía en Matemática siente que la forma de enseñar no se corresponde con sus expectativas. Indica que sus calificaciones en el liceo eran buenas, que estaba en el plan matemático, con lo cual podemos inferir que no había un problema de conocimiento de la matemática y que sus expectativas universitarias se vinculaban con la enseñanza de estas y su futuro laboral. Relaciona este periodo con el punto de inflexión correspondiente a los 13 - 14 años y su molestia, prefiriendo quedarse en casa a tener que ir a aprenderlas. Este pasaje se puede relacionar con lo escrito, donde indica que ella puede aprender por sí misma matemática y que para aprender solo símbolos no es necesario ir al colegio o la universidad. Finalmente, indica que no le transmitían ese "amor" como ella esperaba. Se le consultó con qué está relacionado. A lo que respondió:

Con la pedagogía, con el tema de vamos a enseñar esto. Yo iba con la parada de ser profe de matemática, o sea., ellos decían [docentes universitarios] tienen que aprenderlo porque tienen que aprenderlo..., de hecho, me acuerdo que por eso me salí de la carrera; querían formar más licenciados que profesores, entonces yo no me sentía cómoda y dije ya voy a bajar e ir a educación básica, y no me molestó para nada. Ahora igual estoy feliz acá.

El amor que espera sentir se relaciona con la forma de enseñar y motivar del profesor. Reconoce que quiere ser profesora y espera un cierto entusiasmo del docente. No considera suficiente que se mandate o determine aprender sino que su importancia se sustente en fundamentos pedagógicos.

Posteriormente, indica que los motivos del cambio de carrera se vinculan a esta falta de amor por la enseñanza evidenciada por los docentes de esta carrera. Priorizando la licenciatura, es decir, la disciplina en desmedro de la pedagogía. En otras palabras, se releva el amor por las matemáticas más que la importancia por el sujeto que aprende y la enseñanza en pro del aprendizaje. Igualmente se deja entrever al aludir a "bajar" a un cambio de estatus entre los estudios para secundaria con los de primaria. A continuación, compara profesores de ambas carreras.

acá bajé [educación básica], porque no me sentía cómoda allá [carrera en matemática para secundaria. Llegué a educación básica y me acuerdo de que había un profe de allá [matemático para secundaria] y era lo mismo, me sentía mal [gesto y expresiones de desagrado]..., luego en clases con otra profesora de acá [educación básica], y ahí me empezó a gustar. No elegí la mención en matemática⁴ porque no quiero volver a lo mismo.

En esta diferencia de sensaciones, reflexiona respecto a que la elección de aprender matemática depende de la forma de enseñar del profesor. De hecho, constituye un nuevo punto de inflexión el haber estado en Pedagogía en matemática (secundaria), lo cual marcó un hito en su vida y repercutió en decisiones posteriores.

Para profundizar sobre este volver a lo mismo, la entrevistadora preguntó si se relaciona con una sensación o con una experiencia. A lo cual Fabiola respondió en el siguiente extracto:

es volver a la sensación de saber cómo me están enseñando, es como agghhh [expresión de desagrado], no me gusta cómo me enseñan. Primero viene la sensación, primero en la sala. Yo me acuerdo que cuando estaba en matemática [estudios para ser profesora de matemática en secundaria] me sentaba [contenta] y me decía voy a ser profe, y miraba el profe con una cara y decía: 'es que ustedes tienen que saber, ustedes tienen que ser los mejores y que aquí los licenciados, ojala se vayan a la licenciatura'. Yo decía: 'es que quiero ser profe y a ellos como que no les interesaba esto'. Acá [carrera de Educación Básica] la profe me motiva porque es más dulce para explicar.

Hay una relación con la sensación de desagrado que experimentó en secundaria. No le gustaba cómo le enseñaban en su primer punto de inflexión y vuelve al mismo factor en el segundo. Reconoce que estaba motivada para ser profesora y que esperaba algo diferente en su primera carrera, pero que no se dio y que terminó siendo algo parecido a un entrenamiento. Reconoce ciertas debilidades de la presentación de la carrera por parte de los docentes, y de forma abierta señala la prioridad por los estudiantes de licenciatura, sobre los de pedagogía. Finalmente, agrega que la académica del área de matemática de la carrera de Educación Básica es más dulce, aspecto sobre el cual se le pidió profundizar y agregó:

La profesora da consejos, hace retroalimentaciones, ehhh... nos habla de ciertas cosas, así de la vida diaria, es como diferente a un profe que te enseña una fórmula y tienes que hacerlo. Esta profe, a pesar de que tiene harta disciplina, dice: 'mira, esto es así', da consejos con algo simple y luego pasa a lo complejo, entonces eso como que me es grato, es grato para aprender.

Fabiola reflexiona y reconoce que los consejos, sugerencias y relaciones con la realidad que hace la docente universitaria son las cosas que necesita para estar a gusto y aprender. Releva los conocimientos propios de la disciplina, y agrega la importancia de comenzar con lo sencillo, con los ejemplos básicos, para llegar a lo complejo. Aclara que ser "dulce" significa tener estas características empáticas hacia los estudiantes y que su sensación es de gratitud y comodidad en clases.

Paralelamente, a fin de profundizar, y retomando sus dichos, se le pidió que explicara qué considera una matemática divertida y en qué parte de su vida lo fue:

En educación básica fue más interesante, se podía conversar y preguntar, había un grupo de compañeros y la profesora dejaba sentarse con quien uno quería, todos hacíamos los ejercicios. En la secundaria, las guías eran individuales, uno le preguntaba al profe y sería todo. En educación básica, había más trabajo colaborativo, y en secundaria era más individual.

Fabiola indica que en Educación Básica fue más libre, podía decidir con quién sentarse a trabajar, en contraste con secundaria, en la que el sistema era más regulado y las guías de matemática conformaban el centro y toda la clase. Reconoce como elemento de diversión el trabajo colaborativo y el compartir.

Para concluir, nos comentó que encuentra los números fascinantes y que nunca tuvo problemas con ellos. Que tenía curiosidad, y que esto le ayudaba a resolver problemas. Además, indicó que preguntaba mucho en el colegio, y nos volvió a indicar que no le importaban sus calificaciones y que le gustan las matemáticas, que no le pone una nota a lo que le gusta.

Para terminar se le preguntó qué consideraba importante en este momento de su vida. A lo cual respondió:

Aprender, o sea, yo aprendo. Si me va bien, bien, pero si no lo aprendí ahora, lo aprenderé después. Si le quiero poner una nota a lo que me gusta, entonces me va a estresar toda la vida... Tengo calificaciones sobre el promedio del curso, aunque no son tan buenas; en los talleres me va bien con mis compañeros, porque ahí hacemos cosas más didácticas, ahí tengo buenas calificaciones, es entretenido. No me puedo quejar en estos momentos con matemáticas.

Lo anterior evidencia que ha encontrado equilibrio entre su aprendizaje, lo que entrega en sus estudios y sus calificaciones. Podemos decir que ya ha solucionado sus momentos críticos. Se puede observar también que para ella el trabajo en equipo es decisivo y parte importante de lo que declara como didáctico. Este elemento es reconocido como fundamental para el logro de buenas calificaciones. Igual que en su primer punto de inflexión, enfatizó que la retroalimentación, el trabajo en equipo y la relación de la matemática con la realidad juegan un papel importante para marcar un punto en su vida matemática. Agregó que hay elementos de la didáctica que durante su vida como aprendiz fueron omitidos y que podrían haber marcado una diferencia tanto en sus resultados de aprendizaje como en la entrega que ella pudiera haber hecho en sus estudios. Sorprende en este caso que tuviera una visión de la matemática y el aprendizaje más bien mecánica, al omitir la comprensión de los contenidos. Esta visión mecanicista de la matemática ha cambiado en sus últimos años por la formación pedagógica recibida en los estudios para ser profesora de educación básica.

Es preocupante saber que eventualmente muchos profesores de secundaria formados en esta visión mecanicista de la matemática las llevarán a las aulas.

Caso 2: Greta 23 años, estudios anteriores en traducción e interpretación inglés y español, tiene 4 años como estudiante en la carrera de Pedagogía básica. La entrevista con Greta duró aproximadamente 10 minutos.

En relación con los recuerdos, percepciones y sentimientos con los que asocia la palabra "matemáticas", Greta escribió que

Generalmente con sentimientos de malestar. Connotaciones negativas, incomodidad, miedo, inseguridad, nerviosismo y fracaso.

En cuanto a su autobiografía y la valoración de sus experiencias y autoeficacia, se puede apreciar en la figura 3 que la mayoría de sus experiencias se encuentran en un nivel bajo (menores que 2) y negativo (menores a cero). En relación con su autoeficacia, su autovaloración se encuentra desde muy temprana edad en descenso, comenzando a los 5 años en el nivel 8, para bajar a los 12 años al nivel negativo y mantenerse durante un periodo de aprendizaje importante en el rango negativo. El primer punto de inflexión ocurrió a los 15 años, y se presentó un segundo punto de inflexión a los 20 años.

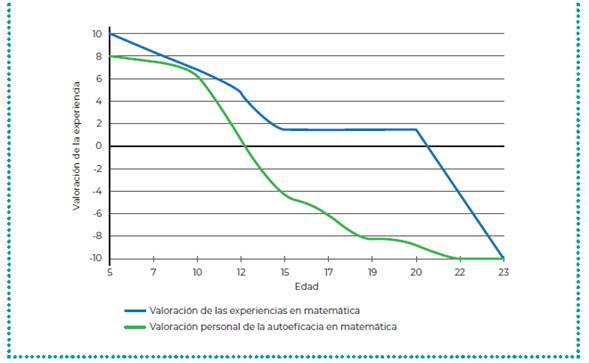
Fuente: Elaboración propia

Figura 3 Representación gráfica de la valoración personal de Greta para sus experiencias y autoeficacia en matemática 

En la figura 3 se puede apreciar que desde los 16 años hasta los 20 Greta tuvo experiencias con poco nivel de agrado, aunque su curva de autoeficacia disminuyó considerablemente en este mismo periodo. Esto nos indica, que en general Greta tuvo malas experiencias durante su época escolar que empeoraron durante sus estudios en la universidad. En cuanto a su visión general sobre su autobiografía matemática, se presenta el siguiente extracto del escrito:

Los primeros años de escolaridad, me gustaban las matemáticas, porque todo era más didáctico y con materiales concretos. Al llegar al 7° y 8° básico perdí el interés, porque era todo en función a guías y ejercicios y el profesor avanzaba rápido. Así, me fui quedando atrás, y en vez de avanzar, retrocedí. En la universidad siempre me desenvolví bien en el área de didáctica, no así en el contenido, por lo que reprobé una asignatura de álgebra por no tener lo suficiente. Hoy que me he preparado más en esta asignatura me da miedo (terror) fallar nuevamente.

Ello confirma lo establecido en la figura 3, y evidencia la baja de Greta a partir del término de la educación primaria, quien reconoce su necesidad de recurrir a materiales concretos, a pesar de su edad, y que el tener clases totalmente centradas en el desarrollo de guías la llevan a quedarse más atrasada que sus pares. Greta reconoce que tiene debilidades en el contenido matemático, pero no con los temas de la didáctica de la matemática, incluso ha reprobado la asignatura correspondiente a álgebra por no saber suficiente matemática, y aunque ya está en una etapa final de su carrera, aún siente temor de reprobar esta asignatura.

En cuanto a la autoeficacia en matemática de Greta, en la figura 3 se puede apreciar que la curva sobre su autopercepción disminuye muy rápidamente y llega al mínimo, es decir, su autopercepción en matemática es muy baja.

En relación con su visión general sobre su autoeficacia, señaló:

La verdad es que en educación inicial todo parece "más fácil", porque no se tiene mayor percepción del grado de exigencia o de la dificultad de la tarea. En enseñanza básica tuve refuerzo permanente en casa, por la menor dificultad en los contenidos. En enseñanza media siempre me costó, "me di por vencida", y en la universidad, me ha costado mucho el álgebra.

Se observa que para Greta el aprendizaje de la matemática, particularmente lo vinculado al álgebra, no es fácil. Recibió ayuda desde primaria para estudiar y manifestó que en enseñanza media se dio por vencida.

La entrevista se centró en los puntos de inflexión de Greta y en el que actualmente se encuentra la participante. Primero, comenzamos con la sensación de malestar, identificando sus experiencias como negativas y con dificultades en el aprendizaje:

es más por la experiencia que he tenido acá en la universidad y en la carrera en general. al entrar a la carrera no pensé que iba a experimentar este sentimiento hacia la matemática, sabía que me iba a tener que enfrentar a asignaturas de didáctica y de contenido de enseñanza de la matemática, pero no pensé que me iba a costar tanto.

Greta reconoce así una dificultad hacia el estudio de la matemática. No se imaginó que en la carrera de Educación Básica tendría que estudiarlas; en este punto se debe aclarar que los contenidos de los programas de esta carrera en el área de matemática corresponden a la matemática de un bachillerato o un equivalente a 12 años de estudio escolar. Ella reitera un sentimiento negativo hacia el estudio de la matemática, sobre lo cual se le pidió que profundizara:

Yo creo que todo se remite a una situación puntual de una asignatura que cursé unos semestres atrás, donde no me fue muy bien, ya que era más contenido... tuvimos un par de diferencias con la profesora; desde el primer momento supo muy bien de que yo no estaba en condiciones de reprobar la asignatura y su nivel de exigencia era mucho mayor a mi rendimiento.

Esta es una situación puntual con una docente universitaria, la cual al parecer, sabiendo sus dificultades para el estudio, subió el nivel de exigencia del curso, en vez de tener una actitud de apoyo. La asignatura no era de enseñanza de la matemática, era una asignatura de conocimiento matemático, y se puede suponer que la docente puso la matemática como un conocimiento duro y difícil, para el cual solo algunos están preparados. Este tipo de creencias por parte de los docentes universitarios puede ser muy perjudicial para los aprendices. Greta continuó especificando sobre esta situación, centrándose en lo que esto significaba para ella, su futuro laboral y su actitud hacia la matemática:

. entonces, claro, esa asignatura la reprobé, y ahora la estoy cursando por segunda vez, y es otra profesora, pero igual, me quedé con esa sensación de que no lo voy a poder lograr, entonces asumir ese desafío nuevamente estando ya ad porta de egresar, me da como miedo, ¿Qué tal si me quedo atrás nuevamente en este ramo y no puedo continuar con mi tesis final el próximo semestre...?

Aunque la situación ha cambiado, y hay otra docente a cargo, mantiene emociones negativas hacia la matemática. La sensación de no lograrlo y de no poder salir de este ciclo se puede ver no tan solo en sus palabras, también se evidencia en la sensación de miedo hacia el contenido, pero por sobre todo este temor de tener que vivir una experiencia para la cual no se siente preparada. Greta se pone en el peor de los casos: volver a reprobar esta asignatura, lo cual nos indica lo fuerte y determinante que es la matemática en la vida de nuestros estudiantes y la importancia que les dan a estas asignaturas.

Para ver si este tipo de situaciones se han vivido antes, se continúa con los gráficos sobre su valoración personal para sus experiencias y autoeficacia en matemática. Se le solicita que comente el periodo desde los 10 a los 15 años, tiempo en el que se ve que hay una baja en ellas:

...yo creo que fue también por el tema de los contenidos, que no son los mismos que se ven en enseñanza básica, entonces el desempeño va a ser distinto, el nivel de exigencia es distinto y las habilidades que uno pone en juego también son distintas.

El cambio del cuarto año al quinto de escolaridad implica una serie de cambios en matemática, que van desde los números naturales y su operatoria a los enteros y fracciones con su operatoria. Aunque actualmente en Chile se trabajan fracciones sencillas en el cuarto año escolar, la operatoria con ellas se ve en los siguientes cursos. Entonces, hay un cambio en los contenidos y también de las habilidades cognitivas de los escolares, lo cual no siempre es considerado por los profesores de aula.

El siguiente extracto de Greta se relaciona con otro punto de inflexión, en otro periodo etario y con otra etapa escolar:

Entre los 15 y los 20, que es toda la etapa de la enseñanza media, hubieron cambios de profesores, de metodologías, entonces todas las personas que tenían un ritmo más lento se iban quedando atrás; entonces yo me empecé a desmotivar, porque no cumplía con el estándar de rendimiento, acorde al nivel. Así es que siempre tuve como un desempeño más o menos del promedio, pero bajo, en todo lo que es álgebra, geometría,, y después, ya en tercero y cuarto medio, funciones y álgebra, ya no cachaba nada.

Aquí reflexiona y establece que para comprender algo en matemática necesita más tiempo que otras personas lo cual no es un problema, salvo cuando hay un profesor, maestro o docente que olvida al sujeto que aprende. Al quedarse atrás, hay una desmotivación y se menciona la palabra "estándar", con la cual se refiere el promedio de notas de un curso según el nivel. Lo anterior deja ver una sensación de inferioridad y segmentación por competencias que no es parte de lo que se busca propiciar.

Greta menciona, además, los contenidos en los cuales le iba mal, y cómo al final de la escolaridad, en "cuarto medio", ya no entendía nada de lo que se hablaba en matemática. Esta es otra de las características de la matemática escolar: los contenidos son presentados con una estructura de "edificio", se necesita saber lo anterior para poder seguir entendiendo (construyendo), de lo contrario, si no se entendió algo en la mitad o en años anteriores, no se puede seguir avanzando. Por eso, sostenemos que es necesario considerar las habilidades y centrar las clases de matemáticas en el desarrollo de éstas, más que en el contenido.

Para continuar, se le solicitó que se describa a ella misma en relación con sus estudios y habilidades en otras áreas:

Si nos remitimos solo a matemática, yo creo que es un poco triste y limitante, porque uno al ver su rendimiento descendido como que te cuesta más, uno se siente más limitado; pero tengo la suerte que esto lo compenso con otras habilidades y destrezas; en otras áreas me va super bien, me va excelente, y básicamente, como que siempre algo de la matemática ha sido como la piedra en el zapato.

En lo anterior se evidencia que la matemática es un problema no superado o latente para ella, asumiéndola como una limitante en su vida, lo que constituye un desafío, pues como docente de primaria deberá modelar su interés y valor por esta área.

Para encontrar algunas soluciones que eventualmente podrían ayudarla a avanzar, seguimos la entrevista con preguntas para identificar y reflexionar sobre sus fortalezas o proyecciones en esta área:

Como trabajo personal, me he estado preparando más, ahora que estoy pasando este ramo nuevamente y me he tratado de convencer y de hacer un trabajo como personal y decir: 'claro, a lo mejor no me fue tan bien porque yo no puse lo necesario para que me fuera bien', así es que ahora le estoy poniendo más empeño y dedicándole más tiempo para ver si realmente es un tema de dedicación o es un tema de capacidad, porque, claro, a lo mejor yo siento que no soy capaz, pero fue porque no le dediqué el tiempo suficiente.

Aquí da un primer paso, reconociendo que todas las cosas requieren de trabajo, en este caso estudio y dedicación, aunque tiende a mezclar sus capacidades cognitivas con la dedicación y el tiempo que se requiere para estudiar matemática. El sentimiento que tiene sobre sus capacidades, que se ha ido gestionando por años, le impide tener una actitud positiva respecto al estudio. Todas las asignaturas requieren de tiempo y dedicación, para algunas cosas las personas requieren más o menos tiempo; esto es parte de las diferencias de los individuos y un buen comienzo para enfrentar el desafío, reconociendo que el logro se vincula con el tiempo dedicado y una actitud más positiva respecto al estudio.

La entrevista continuó con comentarios sobre las diferencias entre las personas, la cantidad de tiempo dedicada al estudio y las preferencias de Greta. Se le preguntó sobre su interés en la matemática:

Esa capacidad, de ser hábil en matemática, no la tengo, pero es porque tampoco me gusta, porque claro que hay otras cosas que sí me gustan y me nace hacerlas, pero en matemática no, tengo como una traba; aparte de lo académico y el rendimiento, es el tema del gusto, no me siento con motivación para hacerlo, ya estoy predispuesta a que voy a fracasar y voy a tener un mal resultado.

Ella reconoce su predisposición hacia el fracaso en matemática, y lo adjudica a sus propios resultados e intereses. Le falta la motivación para estudiar y aprender matemática. Se vuelve a observar este desconcierto de no ser capaz y de no poder enfrentarse al problema. Ante ello, se le solicitó que profundizará sobre sus creencias respecto de sus capacidades y el aprendizaje de la matemática:

... si yo sintiera que soy más hábil o que tengo más capacidad, creo que me gustaría más, y de hecho, me gustaría tener esa habilidad de matemática como otras compañeras, que ven un ejercicio y dicen esto lo puedes hacer así y puedes cambiar estos números por acá, lo puedes interpretar de esta forma, pero a mí me cuesta más. Las personas que saben matemática, nacieron con un don que yo nunca lo voy a poder tener. todo pasa por el contenido. La matemática se manifiesta en otro lenguaje, no así otras asignaturas.

En lo último se aprecia que atribuye al aprendizaje de la matemática un don especial, del cual carece. Esta habilidad consiste en manipular los números y "ponerlos" en ciertos lugares para responder a una pregunta. También la vincula con un lenguaje que ella no entiende y que no es igual al que se trabaja en otras áreas del conocimiento. En ambas respuestas enfatiza su imposibilidad.

De este modo, es posible establecer que Greta está viviendo aún una situación de conflicto y que no logra llegar a un punto de inflexión. Los elementos detectados que generan esta situación se relacionan con características personales de Greta y una falta de motivación para el estudio de la matemática. Igual que en el caso de Fabiola, se puede apreciar una visión mecánica de la matemática, aunque para Greta este mecanicismo es completamente desconocido, infranqueable y no ha cambiado desde su época escolar. El tema de los logros en las evaluaciones en matemática es un tema que no ha superado, y podemos decir que tiene miedo a la matemática, y que, de no superarlo, tendrá dificultades al momento de enseñar esta materia en el colegio.

Discusión

Esta investigación muestra que tanto las vivencias de la etapa experiencial preprofesional como la de socialización profesional vinculada a la formación inicial docente (^{Marcelo y Vaillant, 2009}) plasmadas en la autobiografía activan la reflexión sobre situaciones pasadas, presentes, sus implicancias y su proyección futura, particularmente vinculadas a la manera en la cual cada uno va a enfrentar la enseñanza de ciertas materias (Marcelo y Vaillant, 2009; ^{Lipovec & Antolin, 2014}).

Ahora bien, los mecanismos que los profesores estudiados movilizaron para pasar del estado de inflexión a uno de reflexión y proyección fueron diversos. Incluso, en muchos de ellos, la reflexión transitó desde la indeterminación a la determinación del por qué les pasaba aquello y qué hacer para mejorarlo. En otras palabras, los puntos de inflexión presentes en la autobiografía actúan como activadores de la reflexión, y de allí al compromiso con la acción y la mejora; es decir, la proactividad.

La autobiografía nos aporta relevante información a la hora de contextualizar los aprendizajes a los requerimientos de los aprendices y proyectar futuras prácticas docentes (^{Kelchtermans, 2009}; ^{Stenberg, 2011}; ^{Fernández-Cruz, 2010}). En esta investigación se destacan los puntos de inflexión que aluden a una falta de diversidad metodológica de los profesores con los cuales se relacionaron en su historia en el aprendizaje de las matemáticas, lo cual indica que en la formación de profesores de secundaria y universitarios se deberían incluir métodos diversos de clases asociados a la enseñanza de la matemática. El área de las matemáticas se ve relacionada con una autopercepción de dificultad y bajas competencias que, de no trabajarse, podrían incidir en la manera en que los profesores en formación enfrenten y proyecten la enseñanza (^{Lipovec & Antolin, 2014}; Kassila, 2007; ^{Rivas Flores et al., 2010}).

Los casos aquí presentados son útiles, al ser circunstancias únicas e irrepetibles que nos llevan a reflexionar (^{Righetti, 2006}), y se constituyen en material educativo de apoyo a la reflexión de docentes en formación o en servicio.

Coincidimos con ^{Márquez Jiménez (2016)} en el hecho de que la visión negativa hacia la matemática es un fenómeno generalizado entre las personas, también con ^{Lutovac y Kaasila (2011)} específicamente en cuanto a los maestros de primaria, y sostenemos que los programas de formación docente deben encontrar una forma de mejorar o revertir este fenómeno.

Estos dos casos aportan directamente a la formación inicial de estas docentes y a las de muchos otros. En concreto, el caso de la estudiante que reflexiona y resuelve de manera positiva sus conflictos, nos muestra una alternativa de superar los problemas personales en matemática y nos da luces sobre cómo un determinado suceso, enfrentado con los apoyos necesarios, puede reconceptualizarse en una experiencia que aporta al desarrollo del individuo.

El caso que no resuelve sus conflictos, nos lleva a proponer en cursos de pregrado algunas alternativas, como la biblioterapia, ciclos de reflexión sustentados en casos reales en matemática, en los que la autobiografía y la reflexión sobre lo narrado permita abrir caminos que solucionen esta mala visión.

La formación docente debe hacer todo lo necesario con tal de poder trabajar con la experiencia y la consiguiente percepción, autovaloración y proyección, de manera que no termine siendo una profecía autocumplida, igual que en el efecto Pigmalion, de un fracaso que está llamado a repetirse, que incide en una baja autovaloración y baja estima.

Al Igual que en el caso de ^{Wilson y Latterell (2017)} y en lo propuesto por ^{Bañuelos Márquez (1993)}, en estos casos detectados encontramos que la efectividad de sus maestros no fue el único factor en los puntos de inflexión en la reflexión sobre la experiencia en matemáticas. Uno de los casos explicó su nivel de atracción por tipos o ramas particulares de las matemáticas, así como su dificultad o confusión con otras ramas de las matemáticas. De esta manera, algunos de los participantes describieron una trayectoria caracterizada por la comprensión y el disfrute, seguidos por la incomprensión y el desaliento, o viceversa. Aspecto que también debe ser material de análisis, reflexión y mejora.

Conclusiones

Los resultados de esta investigación permiten establecer que la autobiografía, como activador de la reflexión, aporta relevante información desde distintas etapas vividas por un profesor, y da cuenta de importantes datos sobre la manera en la que se va a enfrentar la enseñanza de ciertas materias.

Entre las temáticas que emergen se destacan las formas de enseñanza, las relaciones que establecen los maestros con los alumnos, los tipos de retroalimentación, la mediación de la experiencia de éxito o fracaso, los énfasis que cada profesor da a sus clases y la manera como apoya a sus estudiantes, entre otras. Temáticas todas de gran relevancia para un docente y de las cuales se espera asuma una postura clara y coherente con los fines de la educación actual. Para ^{Kaasila (2007)}, el análisis de la manera en que los maestros en formación hablan sobre sus vivencias durante sus propia experiencia escolar ayuda a comprender sus propósitos, motivos y acciones, relevando que nada de lo que propiciamos es neutro o independiente de nuestra historia.

De hecho, una historia escolar negativa puede dar pie a una forma revitalizada de enfrentar el aprendizaje en esa área cuando se buscan alternativas de apoyo. Por esto, es necesario incluir la reflexión entre pares en la formación docente, para discutir sobre estos puntos de inflexión; lo cual podría canalizarse en la toma de conciencia de la persona que está en punto de inflexión y que implica reflexionar sobre el problema o sentimiento relacionado con ella de manera intencionada y rigurosa. Ello puede cambiar una historia de vida personal, pero, a la vez, las circunstancias de muchos escolares, y en un ámbito tan determinante y trascendente para su desempeño futuro como lo es la matemática.

Finalmente, al activar la reflexión con la autobiografía se rememoran creencias, problemas, sensaciones, contextos y situaciones que demandan al profesor en formación analizar, reflexionar , como agente activo en la construcción de saberes. Con ello se va creando conocimiento docente (Schón, 1998), se crece en autonomía, valoración, profesionalismo (^{Domingo y Gómez, 2014}), y claramente se asume una postura crítico-constructiva frente a lo que podemos transformar y mejorar en un claro compromiso educativo/formativo tanto en lo individual, profesional como social (Giroux, en Domingo y Gómez, 2014).