Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.183 Medellín Jan./Feb. 2014
https://doi.org/10.15446/dyna.v81n183.36005
http://dx.doi.org/10.15446/dyna.v81n183.36005
A STABILITY AND SENSITIVITY ANALYSIS OF PARAMETRIC FUNCTIONS IN A SEDIMENTATION MODEL
UN ANALISIS DE ESTABILIDAD Y SENSIBILIDAD DE LAS FUNCIONES DEFINIDAS POR PARAMETROS EN UN MODELO DE SEDIMENTACION
CARLOS D. ACOSTA
PhD, Departamento de Matemáticas y Estadística, Universidad Nacional de Colombia, Manizales, cdacostam@unal.edu.co
RAIMUND BÜRGER
Dr.rer.nat., CI2MA y Departamento de Ingeniería Matemática, U. de Concepción, Chile, rburger@ing-mat.udec.cl
CARLOS E. MEJIA
PhD, Escuela de Matemáticas, Universidad Nacional de Colombia, Medellín, cemejia@unal.edu.co
Received for review December 13th, 2012, accepted October 18th, 2013, final version december, 08th, 2013
ABSTRACT: This paper deals with the reliable and efficient numerical identification of parameters defining the flux function and the diffusion coefficient of a strongly degenerate parabolic partial differential equation (PDE), which is the basis of a mathematical model for sedimentation-consolidation processes. A zero-flux initial-boundary value problem (IBVP) posed for this PDE describes the settling of a suspension in a column. The parameters for a given material are estimated by the repeated numerical solutions of the IBVP (direct problem) under systematic variation of the model parameters, with the aim of successively minimizing a cost functional that measures the distance between a space-dependent observation and the corresponding numerical solution. Two important features of this paper are the following. In the first place, the method proposed for the efficient and accurate numerical solution of the direct problem. We implement a well-known explicit, monotone three-point finite difference scheme enhanced by discrete mollification. The mollified scheme occupies a larger stencil but converges under a less restrictive CFL condition, which allows the use of a larger time step. The second feature is the thorough sensitivity and stability analysis of the parametric model functions that play the roles of initial guess and observation data, respectively.
KEYWORDS: Sedimentation of suspensions, sensitivity analysis, degenerate parabolic equation, parameter estimation, discrete mollification.
RESUMEN: Este artículo se dedica a la identificación numérica confiable y eficiente de los parámetros que definen la función de flujo y el coeficiente de difusión en una ecuación diferencial parcial de tipo parabólico fuertemente degenerada que es la base de un modelo matemático para procesos de sedimentación-consolidación. Para esta ecuación, el problema de valor inicial con valores en la frontera (IBVP) en el que el flujo es nulo, describe el asentamiento de una suspensión en una columna. Los parámetros para un material dado se estiman con base en repetidas soluciones numéricas del problema directo (IBVP) con una variación sistemática de los parámetros del modelo, con el objeto de minimizar sucesivamente un funcional de costo que mide la distancia entre una observación dependiente de tiempo y la correspondiente solución numérica. En este artículo se destacan dos aspectos. El primer aspecto es que en el método propuesto para la solución numérica eficiente y acertada del problema directo, se implementa un esquema explícito monótono bien conocido basado en diferencias finitas que usan tres puntos mejorado por molificación discreta. El esquema molificado utiliza una malla de más puntos pero converge con una condición CFL menos restrictiva, lo cual permite usar pasos temporales más grandes. El segundo aspecto es el exhaustivo análisis de sensibilidad y estabilidad de las funciones definidas por parámetros en el modelo y que juegan los papeles de aproximación inicial y dato observado, respectivamente.
PALABRAS CLAVES: Sedimentación de suspensiones, análisis de sensibilidad, ecuación parabólica degenerada, estimación de parámetros, molificación discreta.
1. INTRODUCTION
1.1. Scope
Our goal is the numerical identification of unknown parameters in the flux and diffusion terms for the following initial-boundary value problem (IBVP) for a strongly degenerate parabolic equation in one space dimension:

where A is an integrated diffusion coefficient, i.e.,

The diffusion function a is assumed to be integrable and is allowed to vanish on u-intervals of positive length, on which (1a) turns into a first-order hyperbolic conservation law, so that (1a) is a strongly degenerate parabolic. On the other hand, we assume that f is piecewise smooth and Lipschitz continuous. Under suitable choices of u0, f, a,  and
and  the IBVP (1) may describe a variety of real-world applications like traffic flow [9]. We focus our attention on Equation (1) as a model of the sedimentation-consolidation process of a solid-liquid suspension [8].
the IBVP (1) may describe a variety of real-world applications like traffic flow [9]. We focus our attention on Equation (1) as a model of the sedimentation-consolidation process of a solid-liquid suspension [8].
It is well known that solutions of (1a) are, in general, discontinuous even if  is smooth, and need to be defined as weak solutions along with an entropy condition to select the physically relevant solution, the entropy solution. For the definition, existence and uniqueness of entropy solutions of (1) we refer to [7, 8, 10].
is smooth, and need to be defined as weak solutions along with an entropy condition to select the physically relevant solution, the entropy solution. For the definition, existence and uniqueness of entropy solutions of (1) we refer to [7, 8, 10].
In the present work we are interested in a stability and sensitivity analysis of the parametric model functions. In order to perform the tests, we first proceed with a numerical estimation procedure based on repeated numerical solutions of the direct problem (1) under successive variation of parameters appearing in the coefficient functions f and a. In this phase the main components are the efficient and stable solver of the direct problem and the optimization procedure based on the Nelder- Mead Simplex Method. Our goal is the stability and sensitivity analysis of the resulting inverse problem. Theoretical aspects related to identifiability are not our concern in this paper (but cf., e.g., [11]). By sensitivity analysis we mean an intensive set of tests for the numerical identification of parameters with or without noisy observation data. Our approach follows the methodology of [4] but we acknowledge the existence of other ways to perform a sensitivity analysis, for instance [19].
1.2. Related work and outline of the paper
The discrete mollification method is a convolution-based filtering procedure suitable for the regularization of ill-posed problems and for the stabilization of explicit schemes for the solution of PDEs. For the numerical identification of diffusion coefficients by discrete mollification, see [16] and its references.
Inverse problems for strongly degenerate parabolic equations are of particular interest in the context of the sedimentation-consolidation model. In fact, in applications such as wastewater treatment and mineral processing, the reliable extraction of material-specific parameters appearing in the model functions f and a from laboratory experiments allows the operation and control of continuous clarifier-thickeners handling the same material to be simulated [10, 21]. For the special case A ≡ 0, i.e., when effects of sediment compressibility are absent or negligible, (1a) reduces to a first-order nonlinear conservation law, portions of the function f can be identified by comparing observed space-time trajectories of concentration discontinuities, with trajectories appearing in closed-form solutions for piecewise constant initial concentrations [6, 14]. In the presence of sediment compressibility, closed-form solutions are not available and one has to resort to numerical techniques to solve the parameter identification problem [5, 11].
The paper is organized as follows. Section 2 presents the sedimentation-consolidation model along with details on the schemes for the solution of the direct problem, including a brief description of the mollification method. Section 3 deals with the parameter identification problem, the proposed algorithm, the sensitivity analysis and the effect of noisy observation data. This section ends with some conclusions.
2. THE APPLICATION OF THE MATHEMATICAL MODEL
2.1. Sedimentation model
According to [8, 10] and the references cited in these works, (1) can be understood as a model for the settling of a flocculated suspension of small solid particles dispersed in a viscous fluid, where  is the local solid concentration as a function of height x and time t. For batch settling in a closed column of height L we set
is the local solid concentration as a function of height x and time t. For batch settling in a closed column of height L we set  and
and  ; the function
; the function  denotes the initial solid concentration. The material specific function f describes the effect of hindered settling. We employ here the following typical parametric expression:
denotes the initial solid concentration. The material specific function f describes the effect of hindered settling. We employ here the following typical parametric expression:

where  is the settling velocity of a single particle in an unbounded fluid, C>1 is a dimensionless exponent that quantifies how rapidly the settling velocity decreases (as an absolute value) with increasing solids concentration, and
is the settling velocity of a single particle in an unbounded fluid, C>1 is a dimensionless exponent that quantifies how rapidly the settling velocity decreases (as an absolute value) with increasing solids concentration, and  is a (nominal) maximal solids concentration. The function A is given by (2), where we define
is a (nominal) maximal solids concentration. The function A is given by (2), where we define

where  and
and  are the solid and fluid densities, respectively, g is the acceleration of gravity and
are the solid and fluid densities, respectively, g is the acceleration of gravity and  is the derivative of the material specific solid stress function
is the derivative of the material specific solid stress function 
Among several proposed semi-empirical approaches for  we chose the power law type function
we chose the power law type function

with material-dependent parameters  and
and  The values of
The values of  and
and  characterize the compressibility of the sediment formed by a given material.
characterize the compressibility of the sediment formed by a given material.
Values of the primitive  usually have to be determined by numerical quadrature. However, if f and a are given by (3)-(4) and
usually have to be determined by numerical quadrature. However, if f and a are given by (3)-(4) and  is an integer, then
is an integer, then  can be evaluated in closed form by
can be evaluated in closed form by  for
for  (equation (1a) is strongly degenerate) and
(equation (1a) is strongly degenerate) and  for
for  where the function A is defined by
where the function A is defined by

2.2. Discrete mollification
The discrete mollification method [17, 18] consists in replacing a set of data  by its mollified version
by its mollified version  where
where  is the discrete mollification operator defined by
is the discrete mollification operator defined by

The support parameter  indicates the width of the mollification stencil, and the weights
indicates the width of the mollification stencil, and the weights 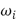 satisfy
satisfy  and
and  for
for  along with
along with  . The weights
. The weights  are obtained by numerical integration of a suitable truncated Gaussian kernel. Details can be found in [1, 2, 3, 16, 20].
are obtained by numerical integration of a suitable truncated Gaussian kernel. Details can be found in [1, 2, 3, 16, 20].
2.3. Discretization of the direct problem
The domain  is discretized by a standard Cartesian grid by setting
is discretized by a standard Cartesian grid by setting  , where
, where  and
and  , where
, where  .
.
We denote by  an approximate value of the cell average of u = u(x, t) over the cell
an approximate value of the cell average of u = u(x, t) over the cell  at time
at time  and correspondingly set
and correspondingly set

We solve (1) numerically using two convergent finite difference methods. The first one [8, 13] has the following form, where  and
and 

Here  stands for the well-known Engquist-Osher numerical flux [12], and
stands for the well-known Engquist-Osher numerical flux [12], and  denotes the standard forward difference operator. Scheme (5) is monotone and convergent under the CFL condition
denotes the standard forward difference operator. Scheme (5) is monotone and convergent under the CFL condition

The second finite difference method is the mollified scheme [2], which is also monotone and convergent and takes the form

This is an explicit method and has the convenient CFL condition

where  . (For the particular mollification weights considered herein, we obtain
. (For the particular mollification weights considered herein, we obtain  .) Clearly, condition (8) is more favorable than (6) since it shows that for a given value of Dx, mollified schemes may proceed by larger time steps. See [2] for more details on this scheme.
.) Clearly, condition (8) is more favorable than (6) since it shows that for a given value of Dx, mollified schemes may proceed by larger time steps. See [2] for more details on this scheme.
3. SENSITIVITY AND STABILITY ANALYSIS
3.1. Parameter identification problem
The inverse problem can be formulated as follows: given observation data  at the final time T > 0 and functions
at the final time T > 0 and functions  ,
,  and
and  , find the flux f and the diffusion function a such that the entropy solution u(x, T) of problem (1) is as close as possible to
, find the flux f and the diffusion function a such that the entropy solution u(x, T) of problem (1) is as close as possible to  in some suitable norm. The inverse problem is solved by minimizing the cost function
in some suitable norm. The inverse problem is solved by minimizing the cost function

Since the functions f and a depend on a vector of parameters, the inverse problem corresponds to the following parameter identification problem:

The functions f and a are associated to the current parameter vector  .
.
We define the piecewise constant function  by
by  for
for  and
and 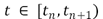 for
for  and
and  and replace
and replace  by a piecewise constant function
by a piecewise constant function  formed by cell averages as follows:
formed by cell averages as follows:

where j = 0,...,  -1. The parameter dependent cost function is
-1. The parameter dependent cost function is
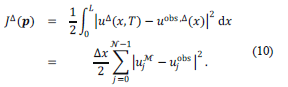
This yields a discrete version of (PI) given by

There are many options for the numerical implementation of the optimization procedure. We selected a globalized bounded Nelder-Mead Method with restarts (MATLAB function fminsearch, see [15] for details), which is a major improvement over the basic simplex method. The strategy is described by the following algorithm. Suppose  , that is, K different parameters are sought.
, that is, K different parameters are sought.
Step 1 Input 
Step 2 for 
 fminsearch
fminsearch
If  then break, end
then break, end
Step 3 End.
3.2. Numerical examples
The reference solution is generated by the corresponding numerical scheme (5) or (7) on a very fine grid. For examples 1, 2 and 3 we consider batch settling in a column of height  m and parameter values
m and parameter values

The objective is to obtain an accurate identification of the parameters  and
and  in eight different instances described in Table 1. Our experiments include clean and noisy observation data. Data at the instant
in eight different instances described in Table 1. Our experiments include clean and noisy observation data. Data at the instant  will play the role of
will play the role of  . Figures 1 and 2 (a) show the reference solution over the whole computational domain and the profile at
. Figures 1 and 2 (a) show the reference solution over the whole computational domain and the profile at  , respectively. The restarting parameter and the tolerance parameter for the optimization are
, respectively. The restarting parameter and the tolerance parameter for the optimization are  and
and  , respectively.
, respectively.
Example 1: Sensitivity to mollification parameters. Clean observation data (no noise added) and  . The results are summarized in Table 2. Here,
. The results are summarized in Table 2. Here,  denotes the number of calls to the fminsearch algorithm,
denotes the number of calls to the fminsearch algorithm,  is the vector of parameter values found,
is the vector of parameter values found,  is the required number of computed solutions of the direct problem,
is the required number of computed solutions of the direct problem,  is the maximum relative error in the result for each parameter (usually due to
is the maximum relative error in the result for each parameter (usually due to  ), and
), and  denotes the total CPU time of each run.
denotes the total CPU time of each run.
Example 2: Sensitivity to initial guess. We randomly generate  initial guesses and carry out the identification task. Each initial guess
initial guesses and carry out the identification task. Each initial guess  is generated in the form
is generated in the form

where  is a uniformly distributed random vectorial variable whose components are between −1 and 1. The results are indicated in Table 3. Here, the average
is a uniformly distributed random vectorial variable whose components are between −1 and 1. The results are indicated in Table 3. Here, the average  of
of  and its standard deviation
and its standard deviation  are included. Additionally, column "# restarts" stands for the number of calls of fminsearch and
are included. Additionally, column "# restarts" stands for the number of calls of fminsearch and  for the number of solutions of the direct problem.
for the number of solutions of the direct problem.
Example 3: Effect of noisy observation data. We randomly generate 100 final profiles and associate them to the previously generated initial guesses. The corrupted profile is generated as follows:

where  and
and  , and
, and  is a uniformly distributed random variable assuming values between −1 and 1. The results are in Table 4.
is a uniformly distributed random variable assuming values between −1 and 1. The results are in Table 4.
3.3. Conclusions
ccording to Table 2, most of the identifications are successful and  seems to be the best choice. For the initial guess A the method for
seems to be the best choice. For the initial guess A the method for  does not converge, but it does converge when started with initial guesses close to A. The results in Table 3, corresponding to Example 2, illustrate how by improving the spatial resolution (i.e., reducing ?x) the quality of the identification is increased.
does not converge, but it does converge when started with initial guesses close to A. The results in Table 3, corresponding to Example 2, illustrate how by improving the spatial resolution (i.e., reducing ?x) the quality of the identification is increased.
Table 4 indicates that the level of noise influences the quality of the recovery but stability is never lost.
Summarizing, this parameter identification procedure yields good results for both the basic scheme and its mollified versions but the mollified approach returned advantages not only in CPU time (in s), but also in the error level, the sensitivity to the initial guess and the effect of noise in the data. This well-posed behavior was already suggested by the convex-shape of the cost functional (Figure 3.)
ACKNOWLEDGEMENTS
CDA and CEM acknowledge support by COLCIENCIAS project 1118-48925120 and by Universidad Nacional de Colombia, Vicerrectoría de Investigaciones, Projects 20201007076, 201010011107 and 20101009545. RB acknowledges support by Conicyt Anillo project ACT 1118 (ANANUM), Fondecyt project 1090456, BASAL project, CMM at Universidad de Chile, Centro de Investigación en Ingeniería Matemática ( ) at Universidad de Concepción and Red Doctoral REDOC.CTA, project UCO 1202 at U. de Concepción.
) at Universidad de Concepción and Red Doctoral REDOC.CTA, project UCO 1202 at U. de Concepción.
REFERENCES
[1] Acosta, C.D., and Bürger, R. Difference schemes stabilized by discrete mollification for degenerate parabolic equations in two space dimensions. IMA J. Numer. Anal., 32: pp.1509-1540, 2012. [ Links ] [2] Acosta, C.D., Bürger, R. and Mejía, C.E.. Monotone difference schemes stabilized by discrete mollification for strongly degenerate parabolic equations. Numer. Meth. Partial Diff. Eqns., 28: pp 38-62, 2012. [ Links ] [3] Acosta C.D. and Mejía, C.E. Stabilization of explicit methods for convection-diffusion problems by discrete mollification. Comput. Math. Applic., 55:pp 363.-380, 2008. [ Links ] [4] Berres, S., Bürger, R. and Garcés, R. Centrifugal settling of flocculated suspensions: a sensitivity analysis of parametric model functions. Drying Technology, 28: pp.858-870, 2010. [ Links ] [5] Bürger, R., Coronel, A. and Sepúlveda, M. Numerical solution of an inverse problem for a scalar conservation law modelling sedimentation. In: Tadmor, E., Liu, J-G., Tzavaras, A.E. (eds.): Hyperbolic Problems: Theory, Numerics and Applications. Proceedings of Symposia in Applied Mathematics, vol. 67, Part 2. American Mathematical Society, Providence, RI, USA, pp.445-454 (2009) [ Links ] [6] Bürger, R. and Diehl, S. Convexity-preserving flux identification for scalar conservation laws modelling sedimentation. Inverse Problems 29 (2013) paper 045008 (30pp). [ Links ] [7] Bürger, R. Evje, S. and Karlsen. K.H. On strongly degenerate convection-diffusion problems modeling sedimentation-consolidation processes. J. Math. Anal. Appl., 247:pp. 517-556, 2000. [ Links ] [8] Bürger, R. and Karlsen, K.H. On some upwind schemes for the phenomenological sedimentation-consolidation model. J. Eng. Math., 41: pp.145-166, 2001. [ Links ] [9] Bürger, R. and Karlsen, K.H. On a diffusively corrected kinematic-wave traffic model with changing road surface conditions. Math. Models Methods Appl. Sci., 13:pp. 1767-1799, 2003. [ Links ] [10] Bürger , R., Karlsen, K.H. and Towers, J.D. A mathematical model of continuous sedimentation of flocculated suspensions in clarifier-thickener units. SIAM J. Appl. Math., 65:pp. 882-940, 2005. [ Links ] [11] Coronel, A., James, F. and Sepúlveda, M. Numerical identification of parameters for a model of sedimentation processes. Inverse Problems, 19: pp. 951-972, 2003. [ Links ] [12] Engquist, B. and Osher, S. One-sided difference approximations for nonlinear conservation laws. Math. Comp., 36:pp. 321-351, 1981. [ Links ] [13] Evje, S. and Karlsen, K.H. Monotone difference approximations of BV solutions to degenerate convection-diffusion equations. SIAM J. Numer. Anal., 37: pp. 1838-1860, 2000. [ Links ] [14] Grassia, P., Usher, S.P. and Scales, P.J. Closed-form solutions for batch settling height from model settling flux functions. Chem. Eng. Sci., 66: pp. 964-972, 2011. [ Links ] [15] Luersen , M.A. and Le Riche, R. Globalized Nelder-Mead method for engineering optimization. Computers and Structures, 82: pp. 2251-2260, 2004. [ Links ] [16] Mejía, C.E., Acosta, C.D., and Saleme, K.I. Numerical identification of a nonlinear diffusion coefficient by discrete mollification. Comput. Math. Applic., 62:pp. 2187-2199, 2011. [ Links ] [17] Murio, D.A. The Mollification Method and the Numerical Solution of Ill-Posed Problems. John Wiley, New York, 1993. [ Links ] [18] Murio, D.A. Mollification and space marching. In: K. Woodbury (ed.), Inverse Engineering Handbook. CRC Press, Boca Raton (2002). [ Links ] [19] Petzold, L., Li, S., Cao, Y., and Serban, R. Sensitivity analysis of differential-algebraic equations and partial differential equations. Computers and Chemical Engineering 30: pp. 1553-1559, 2006. [ Links ] [20] Pulgarín, J., Acosta, C., and Castellanos,G. Multiscale analysis by means of discrete mollification for ECG noise reduction. DYNA 159: pp. 185-191, 2009. [ Links ] [21] Zhen, Z., Zhichao,W., Guowei, G., and Zhiwei.,W. Parameter estimation protocol for secondary clarifier models based on sludge volume index and operational parameters. Asia-Pac. J. Chem. Eng., 6: pp. 266-273, 2011. [ Links ]




















