1. Introduction
The possibility of developing systems that allow the management of water resources has been constituted in recent years, in one of the most representative and priority problems worldwide. The main leaders in the different nations of the world, incorporate it into their agendas and development plans. This is due to the enormous concern that is increasing every day, due to effects such as Global Warming, the El Niño or La Niña Phenomena, which affect multiple crops throughout the planet. Specifically, in Colombia, the three phenomena have reached a profound impact on economies and societies. An aspect that demands a lot of attention in areas where the soils are characterized by being arid or semi-arid, and that result to have low levels of availability of this resource and of the requirements that increase steadily [1,2].
Worldwide, the consumption of the precious liquid in agriculture ranges from 70 to 90%, registering efficacy levels of around 50%, at best [1]. For this same reason, we propose an Intelligent Control System based on executable models, through a Simulation Software and through wireless sensors and low-cost electronic elements, to rationalize and optimize water consumption in small, medium and small crops. of large extensions. In a particular way -and as a Case Study-, the Watermelon was chosen for its implementation, since it is a well-known fruit planted in the experimentation zone, the Subregion Sabanas of the Department of Sucre.
The Watermelon, whose origin goes back to the African continent, where it still grows wild [3], is one of the most representative cucurbits for human consumption, due to its important contributions of components to the diet. This, for its high levels of vitamin A, B series and vitamin C. Also, for its levels of minerals, such as potassium, magnesium, calcium, phosphorus, sodium, and of carotenoids, such as lycopene, beta-carotene, phytoene, leutin, phytoene and neurosporene. Also noteworthy are their levels of carbohydrates, essential and non-essential amino acids, and healthy unsaturated fatty acids. But, the most remarkable thing is its high moisturizing value, since the fruit is composed of 90% water [4,5]. This moisturizing aspect is somehow reflected in its high level of water consumption in each of its stages of cultivation. Still, we lack statistics that determine the exact levels of fluid consumption during their life stages, unless techniques such as covariance and vortices are used to measure evapotranspiration [6].
The main producer of Watermelon worldwide is China, with 44.2% of world production; followed by the production registered by Turkey, which represents 3.78% of world production; Iran 2.78%; Brazil 2.38%. These countries constitute around 67% of world production [7]. Colombia registered, for the year 2016, a production of 139,488 tons in 7,799 hectares [7]. In Fig. 1, some of these statistics are shown, where you can see the enormous difference that China makes with all the other countries in the world, regarding the production of Watermelon.
The world production of Watermelon occupies a very important place in international fruit trade, together with other fruit plants, such as bananas, apples, grapes and citrus fruits, since approximately 2.22% of the production of fruits commercialized worldwide, belongs to the Watermelon [8].
In Latin America, especially in Colombia, horticultural crops have grown in recent years, due to the expansion of policies that encourage them [9]. In contrast, in the Savanna Subregion of the Department of Sucre, despite having large areas of land conducive to the cultivation of these and other plants, the growth has not been the same. The main causes are related to the effects of Climate Change and the scarce implementation of technological tools oriented to the field. In view of the above, a technological solution was implemented based on Fuzzy Control Systems oriented to the cultivation and production of Watermelon in the Subregion Savannas of the Department of Sucre. The main objective of this tool was to optimize resources in terms of energy, amount of liquid supplied, cost reduction and fertigation management.
2. Materials and methods
The Control Diffuse System for Watermelon crops was initially proposed in two phases. The first phase was the simulation of the entire Irrigation Controller, taking into account most of the variables that affect the microclimate of a plant, that is, the relative humidity in the air, the temperature of the air around the plant (approximately 1 m3 around), wind speed, solar radiation. All these variables are included in the evapotranspiration parameter, which, technically, establishes the approximate value of water consumption of the plant due to these environmental factors.
In order to obtain the hourly values of these variables, the historical databases of the meteorological stations located in the Savannahs of the Department of Sucre were used, especially the Agrometeorological Station, located at the Green Door Headquarters of the University of Sucre (coordinates 9.31, -75.38 and altitude 160 meters) and the pluviometric station of La Pastora (coordinates 9.29, -75.49 and altitude 58 meters). The record was made in a time schedule organized into 2880 data matrices that relate the measured variables, during the 30 days of the 4 months of harvest in which it is customary to plant watermelon crops in the region, that is, March, April, May and June.
In the database, the seasons between 2008 and 2015 are recorded, that is 23.040 data for each simulated variable, which guarantees the correct implementation of the simulation and the sensitivity of its results, according to Chebyshev's theorem (1) , which was selected to evaluate the quality of the data, considering that its evaluation does not depend on the type of distribution that the data possess, nor should it start from premises or assumptions related to the correspondence that have the distributions of the data with basic distributions such as Gaussian, in studies with discrete variables [10].
This Probability Theorem establishes the maximum acceptable distance between the standard deviation and the average of a random variable so that its result is considered acceptable. Technically, this means that the minimum number of samples used in this Simulation Study are valid [11].
In addition to including meteorological variables in the Simulation Model, mathematical models supported by specialized literature were included to represent the root growth of the Watermelon plant during the entire sowing period [12]. Knowing that the root -in time and in just measure with its growth- also has a direct influence on the water requirements of the plant and, in general, on the plantation.
Likewise, and in order to make a simulation study as complete as possible, capable of recording the largest amount of data that helps determine the respective water requirements of a Watermelon crop, models for runoff, precipitation rate, and the positive vertical growth of the plant (crop coefficient), which has been defined for annual herbaceous plantations by FAO [13]. All these models that are defined and explained in [14], interact with each other through a simulation tool developed in Matlab® using Simulink®, to model the growth, hour after hour, of the Complete System and its water requirements. In Fig. 2, the complete scheme of the control system and the variables included in it are shown.
All the variables of the system as a whole are modeled through the Water Balance Equation (2), used to know the liquid requirements in real time of the crop, after the splicing of all the air and soil census variables. This model was implemented through the Fuzzy Controller designed in Matlab® for the Drip Irrigation Circuit, implementing the "High-Frequency Localized Irrigation" (RLAF) strategy, which was selected for its efficiency to be applied to the test crop [15].
The Water Balance Model that was defined by [12] uses the parameter n to specify the size of the soil particles and the air space between them. Meaning, that a study of the soils where the Watermelon planting was going to be carried out was required. In the present Case Study of the Sabanas Subregion of the Department of Sucre, from previous studies, it was known that these soils are clayey, loam and clay loam type [16]. So the modeling software used the appropriate parameters, but they had to be introduced by the user, to then perform the respective soil study. That is, if the present prototype is to be used in another area of the country or another geographical region, it would simply be enough to carry out a technical study of soils, where the present percentage values of sand, silt, and organic matter are estimated.
Additionally, it should be clarified that Model (2) included the parameter Zr, which represents in some way the rhizosphere of the plant. Therefore, the variation over time of the soil moisture measured directly, that is, ds/dt which turned out to be an important factor was included because it defines the rate of change in real time of said humidity, either during the irrigation or subsequent to it.
By mass balance, the above variables must be balanced to the contribution of the precipitation rate R(t), minus the values of losses of unused liquid, either by infiltration I(t) or by surface runoff Q[s(t); t], the hourly rate by evapotranspiration E[s(t)] and the deep percolation L[s(t)] All these variables depend substantially on the type of terrain and its physical properties, except for Evapotranspiration, that depends on the climatic conditions exposed above, in addition to the height with the sea level of the growing region.
After feeding the Water Balance Model, the Modern Control Theory was used to perform the irrigation, that is, the difference between the reference signal (desired humidity) and the actual crop signal (real humidity) was used to determine the amount of liquid required by it. This difference is called Error Signal in Control Theory; Ideally, it should be tending to zero (ΔE → 0). In this way, and during a period of stability of the system, it was established that both signals are very similar, that is, that the humidity in the soil is approximately equal to the humidity required by the plant and that, through the action of control, execute the value of the final position of the valve that allows the flow of liquid to the terminals, drippers in the present study, ensuring the required delivery of the liquid and optimizing the energy resources of the same. In Fig. 3, the general scheme of what the control system is, is shown.
As can be seen in Fig. 3, the Evaporation Model, or liquid requirement, which was included in the Fuzzy Controller Programming, contains all the aspects that relate to the microclimate of the plant, such as root growth of the roots and the rhizosphere, the already listed meteorological variables, which are provided through the weather station in real time. These values feed the Water Balance Equation, which would be the comparable value through the Controller and, thus, establish the position of the valve, to let the liquid flow to the irrigation terminals in the crop.
To execute all the previous control action, we used the Simulink® tool of Matlab®, which supports the Mamdani diffuse design, based on rules, which defined the position of the valve in a closed range, from 0 to 100% opening or closing, using the closed set between (-1, 1).
The second phase was the implementation of the Irrigation System in a small plot, to establish the behavior of the Controller. For this, the NI-USB-6009 OEM card was used, which had 8 analog inputs (each of 14 bits and with a speed of 48 KS / s), 2 analog outputs (12 bits at 150 S / s), and 12 digital inputs/outputs (I / O). For this case, and by the nature of the variables that fed the Water Balance Model, and, more specifically, the Penman-Monteith Mathematical Model, the inputs/outputs (I/O) were configured for analog variables.
On the other hand, the same software was used as in the simulation, fed with sensors located in a WatchDog Model 2900ET low-cost weather station, with the technical data in the sensors of Table 1. These sensors wirelessly fed the values of the variables meteorology of the Penman-Monteith Models and the Water Balance in the Fuzzy Controller.
Also, the actuator that was implemented was the proportional type solenoid valve MPYE-5-1 / 8 of FESTO with the position sensor, which operates with an operating range between 0 to 5 volts for its maximum and minimum flow respectively [17].
As can be seen in Fig. 4, the valve is placed in intermediate position with closed intervals at 5 volts, that is, there is no liquid flow passage. Likewise, its maximum expression percentage of opening, and therefore of flow, is recorded when the values of supply voltages are from 0 (it goes from position 1 to 2 of the valve) and 10 volts (it passes from position 1 to 4 of the valve), experiencing maximum flow. This graph called VQ (voltage versus flow) is transcendental, because it not only shows the operation of the actuator but suggests the type of membership functions that should be selected in the fuzzy controller for the valve output variable, taking advantage of the fact that the solenoid valve is 5 ways and 3 positions (valves 5/3); having the possibility of executing several rules that use different percentage values in the passage of the amount of liquid to the crop, that is to say q.
Finally, a pre-amplifier voltage board was implemented to couple the signal from the Controller with the Actuator. As Irrigation Terminals, RLAF drippers were used for the dosage of irrigation and additives that were added to the crop, which is commonly called fertigation, considered transcendent for extension crops [19].
2. Results and discussion
The Sabanas Subregion of the Department of Sucre is an area that, for a large part of the year, receives a high solar radiation load that directly affects its crops in summer seasons. In winter, although the loads go down, they are still important, compared with other regions of the country, added to this the concentration of rainfall at some times of the year. Bearing this in mind, the Controller proposed in the present investigation begins with the evaluation of the meteorological characteristics of the study area and, based on them, makes decisions related to irrigation, in real time. Bearing this in mind, the Controller proposed in the present investigation begins with the evaluation of the meteorological characteristics of the study area and, based on them, makes decisions related to irrigation, in real time.
To show the behavior of the climatic variables and their direct affectation in the crops, in Fig. 5 the relation of the temperature and the solar radiation for the Watermelon harvest months is presented.

Source: The Authors.
Figure 5 The behavior of Solar Radiation and Temperature during the Time of Watermelon Cultivation in the Subregion Sabanas
It can be seen that both temperature and solar radiation increase transcendentally at the end of each month and the harvest. This means that the risk to the crop, in terms of water requirements, is increasing as the harvest time passes, both by the growth of temperature and solar radiation, as well as by the growth of the plants and their subsequent entry in the time of reproduction and fruit growth. This is because solar radiation and temperature on the plant directly affect its growth and development [20].
More specifically, Fig. 6 shows the weekly relation of the load of the temperature and solar radiation applied to the crops during the harvest season, so those possible scenarios that would occur during watermelon harvest seasons in the study region.

Source: Source: The Authors.
Figure 6 Weekly behavior of solar radiation and temperature during the Growing Season.
In Fig. 7, an animation of the scheme implemented in the Irrigation System with Fuzzy Control applied in the cultivation of Watermelon is shown. In order for the Fuzzy Controller to work, an input was used based on the error signal, that is, the difference between the magnitude of the desired humidity with the actual humidity of the crop, and, as an output variable, the action of the valve to the control of liquid, in other words the quantity qi that leaves the valve to the Irrigation System.
In Fig. 8, the scheme of the complete Fuzzy Controller is appreciated; The inputs are temperature, relative humidity, wind speed, solar radiation, maximum and minimum temperature. These inputs are connected to the Net Radiation Modules and then to the Evapotranspiration Module, where the liquid consumption is calculated by air. Then, this Evapotranspiration Module is connected to the Water Balance Module that includes Eq. (1), to calculate the total liquid consumption in real time.
In the scheme of Fig. 8, it is observed that the type of soil chosen for this particulate case is Type 2, that is, clay. As previously described, the System is designed so that the user can choose the type of soil on which the Watermelon crop will be grown. Option 1, is arranged for Franco-type soils, and Option 3 for clay loam. If it is required to use the controller in another type of soil, the percentages of organic material, clay and silt can be modified inside the Water Balance Module.
In addition, from the values of the bulk density, as shown in Fig. 9, in the specific case of clay loam soil all the values shown are experimental values taken from studies in the soils where the sowing was prepared. By modifying this data, the Controller would have the ability to adapt to any type of cultivated land.
Likewise, water consumption in the soil of the plant and the plantation was calculated. For example, one of the variables included in the system was the infiltration of water through the soil, so that, using Darcy's Law as an initial mathematical model, it was possible to evaluate the runoff and deep percolation through the speed of infiltration in the different types of soils evaluated, as shown in Fig. 10.
After experimenting and calibrating the complete modeling of the microclimate system and the irrigation of the plants, the Controller was designed to execute the actions required during the liquid quantity control process. For this, some membership functions were implemented, both for the error input variable and for the valve opening output variable. In Table 2, you can see the respective rules based on these membership functions.
These rules are produced when crossing the membership functions and the linguistic labels, and, in a special way, with those defined by the valve output variable, since this must obey the proportional behavior of the electrovalve, which were already shown and analyzed in Fig 4. Also, this set of fuzzy rules are those that decided -based on the error of the humidity level and the rate of variation of this- the position in which the valve will be adjusted, and said rules were obtained by making an analysis heuristic of the possible decisions that the operator would make, if this were a human experienced in the subject.
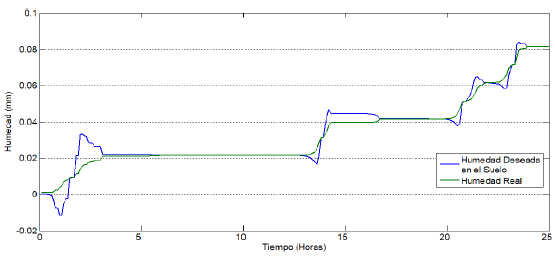
In Fig. 11, the response of the Fuzzy Controller to the desired humidity signal in the culture is shown. It can be seen that the Controller made a significant effort to follow this desired signal, and, from the perspective of Process Control, the System proved to be stable and of optimal behavior because, when calculating the error, evaluating the area under the curve of the difference between the portion of area marked by the desired signal (blue) and the one calculated in real time in the crop (green signal), was less than 2% on average. That is, exactly 1.5421%. The value that is, moreover, very acceptable for systems that work with natural variables and for irrigation districts. Studies such as [21] and [22], were found with error values for Fuzzy Controllers in similar atmospheric conditions, much higher than 4.5%, perhaps due to the fact that the variables associated with the soil are not included in their studies; they only include Evapotranspiration and some meteorological variables.
Based on the information provided by the Controller, it can be stated that the consumption of liquid for the plantation has been optimized, guaranteeing that the quantity of water delivered is approximate that required by the crop.
In Fig. 12, the action of the Controller can be appreciated throughout a day of work. As expected, between 13 and 16 hours a day, there is a higher water requirement and the controller delivers the greatest amount of liquid to the crop. In this way, the energy consumption of the System increases.

Source: The Authors.
Figure 12 Action of the controller for the water requirement of the cultivation.

Source: The Authors.
Figure 13 The action of the valve in the delivery of the liquid to the cultivation.
In Fig. 13, the action of the valve is observed during a day of operation. As can be seen, its behavior is in accordance with what is shown in Fig. 12. Its maximum delivery of liquid is presented at the close time at 15 o'clock, with 20.12 milliliters of water, decreasing as the afternoon passes and then, in the hours at night and for short periods of time, there is also an important requirement: about 17.5 milliliters.
In Fig. 11 to 13, it is shown that the design of the Fuzzy Controller for Irrigation Districts in small, medium and large plantations works correctly, optimizing the water resource and the energy consumption of the System.
Finally, in Fig. 14, the behavior of the error signal at the output of the Controller is shown. It is very important to note that the maximum value is 0.389 (3.897%), that is, the system throughout the harvest season, holds the desired moisture in the crop with a correction factor of less than 4%. In other words, the Controller manages to maintain the water requirements of the crop.
4. Conclusions
The design of the Fuzzy Controller proved to be stable in its behavior, both in the simulation and in its implementation. This ensures the optimization of the water resource and the reduction in the energy consumption of the System. In addition, it was possible to implement using RLAF drippers and fertigation technology, guaranteeing a substantial improvement in production. In percentage terms, the error values do not exceed 1.6% on average, finding maximum values of less than 4%, which is a valid value for a Control System, and even more for agricultural applications, where the tolerability margins can be high.