INTRODUCTION
Soil is a system composed of three phases: solid, liquid and gas. The arrangement of the solid phase or soil matrix determines the geometry of the pore space in which water and air function (Cid-Lazo et al., 2004b). Therefore, it is important, when it comes to knowing the biophysical environment in which the root development of plants occurs, to carry out the physical characterization of the soil (Batey, 2009). This is a very complex process comparable to those studies aimed at grouping properties that delimit a certain behavior of soil functioning (Cid-Lazo et al., 2004b).
With the change in land use, the first modification of a natural ecosystem is compaction (Torres-Guerrero et al., 2016). Soil compaction causes an increase in mechanical density, destroys and weakens its structure, thereby reducing the porosity of soil aeration. Its effects are reflected in a lower development of the root system of plants which implies a lower vegetative development and impairment of agricultural yields (Gutiérrez-Rodríguez et al., 2014).
Vertisols occupy an area of 335 million ha worldwide, generally in semiarid tropical areas, with annual rainfall ranging between 500-1000 mm. Large areas remain in disuse or are only dedicated to extensive uses (livestock, woodcutting, charcoal burning or similar work) that range from smallholdings that produce crops after the rainy season to small and large-scale irrigated agriculture (IUSS Working Group WRB, 2015).
In Cuba they cover an area of about 695,000 ha (Hernández-Jiménez et al., 2014). They are intensively dedicated to the cultivation of sugar cane and rice. Livestock production occupies 50% of agricultural areas (Cid-Lazo et al., 2016).
These soils are characterized by presenting a layer 25 cm or thicker in the first 100 cm of depth, with slickenside or wedge-shaped aggregates inclined longitudinally between 10-60 ° with respect to the horizontal. 30% or more of clays are in the fine earth fraction in the 0-18 cm deep layer or in the Ap horizon and cracks that open and close periodically (Soil Survey Staff, 2010).
They have the peculiarity that, when they yield or absorb water, their apparent volume changes, with the consequent reorganization of the material (Cid-Lazo et al., 2004a). In this way, the apparent density of the soil constitutes an indicator of how the physical properties affect the dynamics of water in the soil, its availability and use by plants (Yang et al., 2016).
In this way, the concept of physical fertility is inseparable from the general fertility of the soil (Cid-Lazo et al., 2006). Likewise, when evaluating changes in the physical quality of soils, the use of multivariate statistics allows a better perception and interpretation of the interactions between the variables involved (Mota et al., 2014). Furthermore, in recent years, hydropedology has become a multidisciplinary science that integrates the fields of research corresponding to pedology and hydrology (Lin et al., 2006).
For the aforementioned reasons, the objective of this work is to determine, through multivariate analysis, the hydropedological behavior of a Chromic Vertisol under different plant covers.
MATERIALS AND METHODS
The work was developed, in 2019, in areas of the Guaro Experimental Block (centroid: 20°40′8.46″ of latitude N and 75°46′9.58″ of longitude W), belonging to the Provincial Research Station of the Sugarcane (EPICA) from Holguín, Cuba, at 17.4 m.a.s.l. The average annual rainfall is 1,067.6 mm, the monthly average temperature is 25.6° C. This region has a tropical rainy climate; it has dry winters and humid summers; registered as Aw, according to the Köppen climate classification. (Peel et al., 2007).
Three types of plant covers were analyzed (natural pasture, sugarcane and secondary forest) established on a Calcium Gleyic Chromic Vertisol (Hernández-Jiménez et al., 2015). The areas of the three vegetation covers were digitized using the MAPINFO 12.0 software in independent layers. Three random points within the limits of each one were generated using the QGIS 3.10 software (Figure 1). In these points, the soil penetration resistance, soil bulk density, gravimetric moisture, and volumetric moisture were determined.
To determine the soil penetration resistance, an impact penetrometer model IAA / Planalsucar-Stolf was used, with the impacting mass of four kg set at a height of 0.40 m. The transformation of the number of impacts per dm to megapascals (MPa) was carried out through the mathematical expression proposed by Stolf (1991):
Where RP is soil penetration resistance, and N is the number of impacts per dm. These results were expressed in constant intervals (0.10 cm), up to 30 cm deep.
Undisturbed samples were taken at the same depths mentioned above with cylinders of 105.35 cm3 in volume. The wet soil mass was determined, and the samples were placed in a stove at 105° C until they reached a constant weight. With the data obtained, soil bulk density was determined (Cid-Lazo et al., 2004a; Cid-Lazo et al., 2006):
where Da is soil bulk density, mss is dry soil mass, and V is the cylinder volume.
Gravimetric moisture was also obtained, using the equation proposed by Cid-Lazo et al. (2004a) and Cid-Lazo et al. (2006):
where θg is the gravimetric moisture, msh is the wet soil mass, and mss is the dry soil mass. The volumetric moisture was determined from equations (1) and (2) (Cid-Lazo et al., 2004a; Cid-Lazo et al., 2006):
A principal component analysis (PCA) was performed on the non-partitioned data matrix to identify the variables that explain the variance of the data. Subsequently, an analysis of canonical correlations was carried out to verify associations between two qualitative sets of variables (set_1: gravimetric moisture and volumetric moisture, which represent soil moisture; set_2: soil bulk density and soil penetration resistance, which define soil compaction). Statistica 7 and Statgraphics Centurión XV.II software were used for statistical analysis.
RESULTS AND DISCUSSION
The 1st and 2nd components explain 71.97 and 11.12% of the variance, respectively, for a cumulative percentage of 83.09%, as a result of the linear combination of the 12 variables studied. The eigenvalues of the two components were above 1 (See Table 1).
Table 1. Eigenvectors of the principal component analysis.
| Variables | 1st component | 2ndcomponent |
|---|---|---|
| Gravimetric moisture 0-10 cm | 0.832365 | 0.437736 |
| Soil bulk density 0-10 cm | -0.130912 | -0.957134 |
| Volumetric moisture 0-10 cm | 0.897024 | 0.029898 |
| Soil penetration resistance 0-10 cm | -0.385339 | -0.801590 |
| Gravimetric moisture 10-20 cm | 0.698635 | 0.568651 |
| Soil bulk density 10-20 cm | -0.386745 | -0.871434 |
| Volumetric moisture 10-20 cm | 0.721587 | 0.366494 |
| Soil penetration resistance 10-20 cm | -0.586691 | -0.772924 |
| Gravimetric moisture 20-30 cm | 0.841134 | 0.449639 |
| Soil bulk density 20-30 cm | -0.744081 | -0.314113 |
| Volumetric moisture 20-30 cm | 0.797638 | 0.419031 |
| Soil penetration resistance 20-30 cm | -0.833466 | -0.412994 |
| Eingenvalue | 8.635828 | 1.334533 |
| Total percentage of variance (%) | 71.97 | 11.12 |
| Cumulative eingenvalue | 8.635828 | 9.970361 |
| Cumulative percentage of variance (%) | 71.97 | 83.09 |
The greatest variation (1st component) given, fundamentally, by the properties related to moisture in the first 20 cm and by hydropedology in the depth of 20-30 cm. As for the 2nd component groups, variation is given by the properties related to soil compaction in the first 20 cm of depth. The 1st component is 6.47 times greater than the 2nd. In both components, there is a contrast between the hydropedological properties that represent soil moisture and those that determine soil compaction.
In the case of the 1st component, as its correlation with moisture is positive, increasing the value of this component increases the water content in the soil, which does not occur with soil compaction in the 20-30cm layer (negative correlation). With respect to the 2nd component, as its value increases, a decrease in soil compaction will occur in the first 20cm of depth (negative correlation).
Figure 2 shows that there are two large groups, one formed by soil moisture and the other by soil compaction. Furthermore, a direct (positive) relationship is observed between soil bulk density and soil penetration resistance. On the contrary, an inverse (negative) relationship was found between soil compaction (represented by soil bulk density and soil penetration resistance) and soil moisture (gravimetric and volumetric moisture). This contrast is more notable between said water content in the soil and the soil bulk density and soil penetration resistance in a depth of 20-30cm.
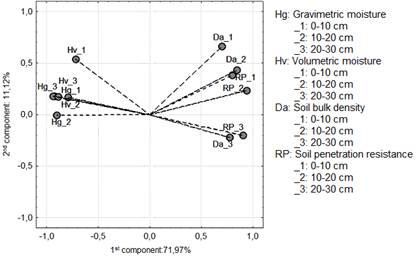
Figure 2. Physical properties dispersion in the principal component analysis. Da: soil bulk density; RP: soil penetration resistance; Hg: gravimetric moisture; Hv: volumetric moisture.
The changes caused by soil moisture in soil bulk density are given by the high content of montmorillonitic clays of Vertisols, which causes these soils to contract and expand constantly under conditions of alternating humidity. This fact affects the variations of soil bulk density.
The evidence suggests that the increase in soil compaction, with the consequent reduction of the pore space, hinders the entry of water into the soil, its movement through it, and its storage in a form available to plants. This reduction in the volume of water that can be used by the plants is accompanied by a decrease in root development, which reduces the space explored by the roots in search of water and nutrients present in the soil.
Hamza and Anderson (2005) state that the increase in moisture favors the decrease in the volumetric density of the soil, since the water molecules in the pore space of the soil prevent the approach of the soil particles. As the moisture decreases, the soil contracts, thus decreasing its volume and increasing its density. Clay soils turn out to be very susceptible to these wetting and drying cycles.
Gao et al. (2016) found, in the first 50 cm of depth, an increase in soil bulk density and the volume of micropores from the surface towards the lower layers of the profile of a soil classified as Vertisol, in Lishu county, Jilin province (China). The increase in soil bulk density caused, especially in non-tillage areas with low soil moisture content, an increase in soil penetration resistance.
In the same way, Jorbenadze et al. (2017), when studying the physical properties of the soils of Georgia, found that Vertisols showed an increase in soil bulk density with depth. This caused a decrease in the maximum capacity of the soil to store water when all pore volumes are full of water (saturation water); of the amount of water contained in the soil previously saturated after the excess has been drained by the gravity force action, and the percolation speed has decreased considerably (water at field capacity). Decrease too, the moisture content of the soil with which the plants cannot replace enough water to regain their turgor (permanent wilting point), and of the amount of water available for the development of the crops that is between the field capacity and the permanent wilting point (usable water).
The magnitudes of the Canonical Correlation analysis, in which the two canonical functions have highly significant values is depicted in Table 2. In the case of the first function, it is especially strong due to its high canonical correlation (0.980682). Wilk's lambda (λ), close to 0, indicates that the independent variables account for almost all of the variance.
Table 2. Magnitude of the relationships that exist between the two sets.
| Eingenva lue | Canonical correlation | Wilk' lambda | Chi-square | Deegrees of freedom | P-value |
|---|---|---|---|---|---|
| Canonical function 1 | |||||
| 0.961737 | 0.980682 | 0.0107241 | 106.579 | 4 | 0.0000 |
| Canonical function 2 | |||||
| 0.719728 | 0.848368 | 0.280272 | 29.892 | 1 | 0.0000 |
For the second function, the value of its canonical correlation (0.848368) is also high, although Wilk's lambda shows that there is a lower variance accounting for the independent variables. Being 1-λ equivalent to the regression coefficient (Badii et al., 2007), it is considered that for the variables corresponding to the first function r2 = 99% and for the second, r2 = 72%.
From the construction of linear combinations between the variables of each set, where the variables were standardized from the subtraction of the mean and the division between the standard deviation, the largest correlations were found. The first associated canonical function is:
The second associated canonical function is:
It is seen that in both canonical functions, there is a primary relationship between volumetric moisture and apparent density, with some contributions from gravimetric moisture and resistance to penetration.
Figure 3 shows the correlation between soil moisture (set of explanatory variables CVARA_1) and soil compaction (set of explained variables CVARB_1). It can be seen that the relationship is linear and with a regular dispersion around the central values of the model, although with a certain discontinuity for the values found in the depth of 20-30 cm.
In this way, any variation that occurs in the soil moisture content will cause changes in its compaction. Furthermore, the grouping of the correlations between the hydropedological variables by depths and not by plant covers is notable. Therefore, changes in soil moisture and soil compaction are more influenced by the depth of the soil than by plant covers. In addition, there are neighborhoods between depths of 0-10 and 20-30cm. The 10-20 cm layer is more spaced and with greater discontinuity. This behavior may be due to the fact that the limits between horizon A and B and the highest values of soil compaction are found at this depth.
Krüger et al. (2018) point out that there is a correlation between soil penetration resistance and soil moisture content. The latter is a variation factor when the former is measured in soils with different degrees of wetting. In this way, it is useful to determine the soil penetration resistance in analogy with the detection of problems concerning the uptake and movement of water in the soil.
Millán et al. (2013), evaluated the effect of the incorporation of biomass on the compaction curve and studied possible alterations in the density and moisture of the soil in a Typical Haplustert located in the municipality of Sincelejo, department of Sucre (Colombia). They found that, for above the maximum soil bulk density (determined by the Proctor test), the increase in soil moisture caused a decrease in soil compaction. Therefore, the variations in soil bulk density depended on the values of said moisture.
CONCLUSIONS
In Principal Components Analysis, the first two components make the greatest contribution to the variance, with 83.09% of the total variance. The highest contributions (1st component) to the total variance are given by moisture at all depths and by soil bulk compaction at a depth of 20-30 cm. The 2nd component is influenced by the soil compaction in the layers 0-10 and 10-20cm deep. There is a contrast, at all depths, between the variables that characterize the state of the solid phase (soil bulk density and soil penetration resistance) with those that describe the liquid phase of the soil (gravimetric and volumetric moisture).
The Canonical Correlation analysis shows the existence of a correlation between the sets CVARA_1 (gravimetric and volumetric moisture) and CVARB_1 (soil bulk density and penetration resistance). The first two sets of canonical variables show a strong correlation (0.980682 and 0.848368, in each case). This is linear and is regularly dispersed along the central values of the model, with a notable grouping by depth.
There is a strong interrelation between the liquid and solid phases of Vertisols. Variations in soil bulk density and penetration resistance affect the reduction or increase of the moisture content in the pore space of these soils.
























