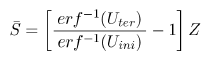Introducción
La disyunción columnar en rocas volcánicas es el patrón de diaclasas que resulta de la contracción y deformación de los materiales durante el enfriamiento y emplazamiento de lavas y corrientes de densidad piroclástica (CDP). Este fenómeno ha adquirido atención por parte de los geocientíficos a nivel mundial, aunque en Colombia hay aún un vacío en el conocimiento sobre estas estructuras. En general, los patrones de diaclasas incluyen columnas de diferentes dimensiones y orientaciones y geometrías poligonales cuando las columnas son observadas en vista de planta. En la sección vertical de una unidad de flujo de lava o de depósito de CDP, se pueden apreciar alternancias entre columnas muy regulares en dimensiones y orientación y zonas en donde las columnas son irregulares y con orientaciones variables (Figura 1). Estas zonas se conocen como facies columnata y facies entabladura, respectivamente (Bakewell, 1813; Tomkeieff, 1940). Las columnas de facies columnata tienen ejes perpendiculares a la superficie de enfriamiento, son generalmente paralelas entre sí, están regularmente espaciadas y tienen una tendencia hexagonal en la geometría de sus secciones ortogonales (Woodell, 2012). Por otra parte, la facies entabladura tiene columnas que se arquean, con ejes inclinados, desorganizadas, y que terminan unas contra otras. Generalmente, la entabladura puede separar dos niveles de columnatas (Spry, 1962) o pueden presentarse solamente dos facies, una columnata inferior y entabladura superior (Walker, 1986).

Figura 1 A. Fotografía de un afloramiento de lavas con disyunción columnar. El sitio, conocido como “La Calera”, está ubicado al suroccidente del volcán Azufral (Nariño) cerca a la vía Túquerres-Tumaco. B. Foto editada señalando rasgos notables de la disyunción. Las líneas discontinuas amarillas marcan de manera aproximada los límites entre facies. Las líneas continuas azules señalan las estrías, marcas dejadas por la propagación de las diaclasas al interior del flujo.
En Colombia, existen algunos estudios principalmente descriptivos de disyunciones columnares, como los de Naranjo-Henao y Ríos-Alzate (1989) , Calderón et al. (2017) , Flórez (2017) , Rave-Bonilla (2019) , Forero y Sánchez (2021) y Rave-Bonilla y Sánchez (2021). Hasta el momento, sin embargo, no se tiene conocimiento de un estudio detallado sobre los mecanismos de formación de estructuras columnares, el análisis de la geometría o la historia térmica de varios sitios en Colombia. Por eso, la presente investigación se enfoca en el estudio de las relaciones entre los distintos parámetros dimensionales y geométricos que presentan las columnas y sus estructuras, además de la definición de cómo, a partir de estas propiedades intrínsecas, se puede inferir el tipo de mecanismo de enfriamiento predominante en su formación. Se utilizan observaciones generales de campo en un grupo de catorce afloramientos y mediciones detalladas en siete afloramientos, la mayoría ubicados en las cordilleras Central y Occidental, y un sitio en el norte de la isla Santa Catalina (Figura 2, Tabla 1).

Figura 2 Mapa de Colombia con la localización de afloramientos (círculos blancos), cuya geometría poligonal fue estudiada mediante inspección visual directa o a través de fotografías de alta resolución. En cada recuadro, el panel superior muestra las geometrías observadas en vista de planta (aproximadamente ortogonal a la elongación de las columnas). En los sitios Cristales y Distrito de Riego se usaron mosaicos de fotos, no necesariamente contiguas, para obtener una muestra representativa. Cuando los polígonos no pudieron ser confirmados, se dibujaron solo los lados visibles y se omitió el relleno. La línea negra gruesa en la parte inferior derecha representa 1 m de longitud. El panel inferior de cada recuadro es un diagrama de barras de la distribución de los tipos de polígonos (T= número de polígonos confirmados, N = número de lados en cada polígono). La Tabla 1 muestra información adicional sobre los sitios, incluidos los resultados de otros sitios cuyos datos no se muestran en la figura. Los afloramientos en los cuales se realizaron mediciones detalladas de la geometría o las dimensiones de las columnas, usando software de procesamiento de imágenes, se han resaltado con un círculo amarillo.
Tabla 1 Datos de los sitios con disyunción columnar estudiados en Colombia. Se incluyen las observaciones de campo a través de fotografías de alta resolución.
| Nombre del sitio | Coordenadas (N, W, en grados decimales) | Litología | Edad | Número de polígonos confirmados | Geometría más común | Referencia (litología, edad) |
|---|---|---|---|---|---|---|
| *Basalt Cay | 13,399639, 81,383330 | Lavas dacíticas | Neógeno | 60 | Hexágonos | Álvarez-Gutiérrez et al. (2014) |
| Alto de ventanas | 4,919579, 75,270285 | Lavas andesíticas | Cuaternario (Pleistoceno temprano-medio) | 6 | Tetrágonos | Ceballos-Hernández et al. (2020) |
| Alto la Llorona | 4,920555, 75,272624 | Lavas andesíticas | Cuaternario (Pleistoceno temprano-medio) | 6 | Tetrágonos | Ceballos-Hernández et al. (2020) |
| Domo San Cancio | 5,04522, 75,49866 | Lavas andesíticas | Cuaternario (Pleistoceno temprano) | 36 | Tetrágonos | Thouret et al. (1990) ; Osorio et al. (2018) |
| *Carros de Piedra | 5,02115, 75,19165 | Lavas andesíticas | Cuaternario (Pleistoceno temprano) | 68 | Hexágonos | Ceballos-Hernández et al. (2020) |
| *Domo Victoria | 4,99628, 75,43698 | Lavas andesíticasdacíticas | Cuaternario (Pleistoceno tardío) | 9 | Heptágonos | Mosquera et al. (1998) ; González (2001) ; Martínez et al. (2014) |
| Distrito de Riego | 2,48776, 75,80969 | Tobas vítreas, cristalinas, líticas, riolíticas | Jurásico | 23 | Pentágonos | Marquínez et al. (2002, 2006), Flórez (2017) |
| La Calera | 1,08779, 77,77590 | Lavas andesíticasbasaltos | Neógeno tardío | 117 | Pentágonos | González et al. (2002) ; González y Zapata (2003); Torres et al. (2005) ; Flórez (2017) |
| Manzanillo (Santa Rosa de Cabal) | 4,917655, 75,639914 | Lavas andesíticasdacíticas | Cuaternario (Pleistoceno temprano) | 9 | Pentágonos, hexágonos | Forero (2020) ; Pulgarín-Alzate et al. (2020) |
| Los Ataúdes | 3,71392, 76,45677 | Lavas basálticas, diabasas | Cretácico temprano | 25 | Hexágonos | McCourt (1984) ; McCourt et al. (1984) ; Flórez (2017) |
| Cristales- Negritos | 4,80000, 75,1000 | Lavas andesíticas | Cuaternario (Pleistoceno temprano) | 3 | - | Ceballos-Hernández et al. (2020) |
| Cristales | 4,80000, 75,0000 | Lavas andesíticas | Cuaternario (Pleistoceno temprano) | 16 | Hexágonos | Ceballos-Hernández et al. (2020) |
| Cristales- Peñón | 4,80000, 75,0100 | Lavas andesíticas | Cuaternario (Pleistoceno temprano) | 7 | Hexágonos | Ceballos-Hernández et al. (2020) |
| Puente Ricardo Chica-Herveo | 5,07830, 75,20878 | Tobas andesític | Cuaternario (Pleistoceno tardío-Holoceno) | 9 | Tetrágonos | Méndez-Fajury (1989) ; Cepeda (2000) |
En los sitios marcados con * no se realizó inspección visual directa.
Marco teórico
Aunque la disyunción columnar es un fenómeno muy común y se han realizado múltiples observaciones, el mecanismo de generación de los muy variados grupos de diaclasas aún es tema de discusión. Algunas de las investigaciones recientes sobre los mecanismos de selección de escala en las disyunciones columnares examinan el problema llevando a cabo experimentos controlados, usando materiales como las suspensiones de almidón de maíz y agua (Goehring et al., 2006; Goehring, 2008) o el lodo en desecación (Goehring et al., 2015); se ha encontrado que el tamaño de las columnas depende inversamente de la velocidad del frente de contracción durante su formación, inferencia apoyada en observaciones de campo en flujos de lava solidificados.
Geometría de los patrones poligonales en la disyunción columnar
Se ha propuesto que la geometría de las redes poligonales en la disyunción columnar evoluciona sistemáticamente desde un estado primario tetragonal (cuadriláteros) hasta un estado maduro con redes hexagonales (Ryan y Sammis, 1981; Aydin y DeGraff, 1988; Budkewitsch y Robin, 1994). Las observaciones revelan que existen tres tipos de intersecciones entre diaclasas, llamadas tipo T, Y, y X. Las intersecciones de tipo T resultan en la formación de polígonos tetragonales; en las de tipo Y, las diaclasas forman ángulos aproximadamente de 120°; y en la intersección tipo X, los patrones son formados por dos uniones tipo Y.
De acuerdo con lo anterior, Gray et al. (1976) demuestran, mediante métodos estadísticos, que, para un plano dividido en una red de polígonos convexos, el número promedio de lados por polígono está dado por la relación:
Donde fn es la frecuencia relativa de polígonos de N lados y χ N , el índice de hexagonalidad, que también es una medida de la madurez del patrón poligonal. Si χ N = 0, se tiene un patrón perfectamente ordenado con todos los polígonos de seis lados; mientras que χ N = 1 indicaría que todos los polígonos son de cinco o siete lados. Con χN = 0,80, el icónico afloramiento de la Calzada del Gigante en Irlanda es considerado uno de los patrones de disyunción columnar más maduros y ordenados que se hayan registrado (Budkewitsch y Robin, 1994; Phillips et al., 2013).
Relación entre el tamaño de estrías y la longitud de lado de columna
Las estrías son bandas aproximadamente paralelas que se aprecian en las caras de las columnas, y son
Donde J T , J Y y J X son las fracciones de las intersecciones tipo T, Y y X, respectivamente, presentes en la red poligonal. De la ecuación 1, se puede predecir que, si existe una mayor frecuencia de intersecciones tipo Y, ñ tiende hacia el valor de seis. Por otro lado, para calcular la desviación o la dispersión de una red poligonal alrededor de un valor, por ejemplo, ñ =6, se puede utilizar el índice de hexagonalidad propuesto por Budkewitsch y Robin (1994) , el cual está dado por la siguiente ecuación:
causadas por eventos sucesivos de propagación de las diaclasas al interior de la lava o depósito de CDP en enfriamiento (Figuras 2 y 3). Algunos estudios sobre el tamaño de estría y la longitud de lado de las columnas sugieren una correlación lineal positiva entre estos dos parámetros, y una relación inversa con la velocidad de enfriamiento (DeGraff y Aydin, 1993). Dado que las columnas con mayor diámetro se desarrollan en lavas o depósitos de CDP que se enfriaron lentamente, mientras que las de menor diámetro se forman durante enfriamiento más rápido, el tamaño de las estrías varía proporcionalmente al ancho lateral promedio de las columnas (Ryan y Sammis, 1978). Para hallar la relación entre tamaños de estría y longitud de lado de polígono, es importante tener en cuenta el tipo de mecanismo de enfriamiento que predomina.

Figura 3 Ilustración de las medidas tomadas a las columnas en campo o procesadas por medio de software. L = longitud de lado de polígono; A = área encerrada por el polígono; θ = ángulo interno; N = número de lados del polígono; D = diámetro de la columna; S = tamaño de estría.
En un flujo de lava o depósito de CDP, la disipación de calor hacia el ambiente externo causa simultáneamente la formación de corteza sólida y la contracción del material. De este modo, se logran dos condiciones fundamentales para que surja la disyunción: la generación de esfuerzos tensionales (por la contracción) y la existencia de un material susceptible de fractura (la costra sólida que se va formando). De acuerdo con Turcotte y Schubert (2002) , asumiendo un mecanismo puramente difusivo (conductivo) de disipación de calor, la propagación de las diaclasas en el material sólido sucede desde una zona de acumulación de tensión térmica inicial (más externa) a otra de tensión térmica final (al interior del flujo), y las tensiones están relacionadas con una diferencia de temperatura, por medio de la siguiente ecuación:
Donde α es el coeficiente volumétrico de contracción térmica; E, el módulo de Young, y υ, la relación de Poisson. Se puede asumir que el tamaño de estría representa la distancia entre dos isotermas fijas T=T ini (temperatura de iniciación de grieta) y T=T te (temperatura de terminación), asociadas a su vez a σ ini y σter. En este sentido, Goehring (2008) propuso que esta relación entre las temperaturas inicial, final y el tamaño promedio de estría S ¯ está dada por:
Donde U= (T − T0 )/(T1 − T0 ) y z es la distancia de avance del frente de fractura respecto a una margen del flujo.
A partir del estudio de emplazamientos de flujos de lava en Canadá y Estados Unidos, Goehring (2008) propuso que, en un estilo conductivo de disipación de calor, la altura promedio de estrías en una posición vertical particular, z, representa la distancia entre las isotermas fijas T=T ini y T= T ter cuando la estría fue formada. Así, en este trabajo se modeló la evolución del campo de temperaturas dentro de un flujo de lava, resolviendo la ecuación 4 para el cambio de temperatura, ∆T=T ini− T ter, a través de una estría, con los siguientes valores iniciales: T ini = 1090°C (temperatura de emplazamiento), T 0= 20°C (temperatura inicial del sustrato), T ter = 750°C (temperatura de transición del vidrio, Tg). De acuerdo con el trabajo mencionado, este análisis térmico puede ser aplicable a una amplia gama de composiciones de lavas.
Por otro lado, para encontrar la relación entre el tamaño de estría y la longitud de lado, cuando la disipación de calor ocurre por convección asistida por grietas, Christensen et al. (2016) proponen:
Donde z´=z/R, y R es la representación de la longitud de escala del flujo; esto implica que:
Combinando las ecuaciones 5 y 6, se obtiene:
Donde L¯ es la longitud promedio de lado del polígono formado en la columna y Pe es el número de Péclet, un valor adimensional que representa la proporción entre la tasa de convección y la tasa de difusión en un sistema de transporte (de calor, en este caso). En regímenes dominados por difusión, P e < 1, mientras que en los regímenes donde domina la convección, P e > 1.
Despejando, la ecuación 7 puede reescribirse en términos del número de Péclet:
Y dado que
Combinando 9 y 8, se encuentra que:
Donde ν es la velocidad linear de flujo (de calor), κ es la difusividad térmica.
Por tanto, bajo la definición del número de Péclet, se puede ver que la velocidad de flujo de calor en la zona convectiva es inversamente proporcional al tamaño promedio de estría.
Metodología
La geometría y las dimensiones de las columnas fueron determinadas a partir de dos aproximaciones que difieren en el nivel de detalle. En primer lugar, se realizó una inspección visual directa de la mayoría de sitios de interés para reconocer las disyunciones y sus facies, ubicar los sitios óptimos para la toma de medidas y definir de manera preliminar la tendencia en organización poligonal. Algunos afloramientos no fueron observados directamente y se recurrió al uso de fotografías de alta resolución. Las fotografías, cuyas orientaciones mostraran los polígonos en vista de planta o en la vista más cercana a la sección transversal a las columnas, fueron seleccionadas para dibujar manualmente los polígonos y realizar una clasificación y conteo de las geometrías. Esta primera aproximación permitió la identificación de 394 polígonos en 14 afloramientos, principalmente ubicados en las cordilleras Central y Occidental, más un afloramiento en Basalt Cay, un pequeño islote al norte de la isla de Santa Catalina (Figura 1, Tabla 1). Solo aquellos polígonos que podían delimitarse claramente fueron marcados y contados. En los polígonos que por diferentes condiciones no era posible un cierre, se dibujaron las líneas más visibles para extraer información sobre el tipo de uniones entre diaclasas.
En segundo lugar, con el propósito de tener una aproximación a la madurez, orden y homogeneidad de los patrones de disyunción, se seleccionaron siete sitios (Figura 1) en los cuales se tomaron las siguientes medidas en las columnas: longitud de lado, L, diámetro máximo, D máx, y mínimo, D mín, conteo de número de lados, N, y de tipos de intersección en las uniones de diaclasas en vista de planta, y se midieron los ángulos internos 𝜃 de los polígonos. Cuando se evidenciaron estrías, se midió el espaciamiento, S, entre estas. Los parámetros geométricos medidos se ilustran en la Figura 3. En los casos donde las condiciones de los afloramientos no permitieron el acceso directo, los datos fueron obtenidos mediante el procesamiento de fotografías de alta resolución con rutinas interactivas (Hetényi et al., 2012) implementadas en MATLAB®. Las rutinas calculan las longitudes de los lados de las columnas y estiman el área, A, encerrada por cada polígono trazado. Para esto, se toma como referencia de escala real, un elemento que esté presente en la foto y del cual se conozca la longitud, como se aprecia en la Figura 4.

Figura 4 Ejemplo de la interfaz interactiva con el programa de procesamiento de imágenes de Hetényi et al. (2012) . Fotografía de un afloramiento en el cual, un objeto de dimensión conocida (vara de Jacob con divisiones cada 10 cm), es usado para determinar la escala de elementos de la imagen (línea verde creada automáticamente por el programa). Los círculos amarillos son marcas definidas por el usuario para señalar los vértices en los polígonos de las columnas. También es posible utilizar el programa para estimar el tamaño de otros rasgos, como las estrías que se puedan notar en las columnas.
Con los datos tomados directamente en campo o derivados del procesamiento de imágenes, se calcularon los parámetros: lado promedio ñ , con la ecuación 1, e índice de hexagonalidad χ Ñ , mediante la ecuación 2. Igualmente, se determinó el tamaño promedio de estrías, S ¯.
Finalmente, para inferir el modo dominante de transferencia de calor durante el emplazamiento, enfriamiento y contracción de las lavas o depósitos de CDP, se usaron las ecuaciones 4 y 8 con los valores medidos de longitud promedio de lado de columna y tamaño promedio de estrías.
Resultados
Madurez de los patrones de disyunciones columnares
En relación con el número promedio de lados, se aprecia que, para los siete sitios analizados, los polígonos corresponden a tetrágonos, pentágonos, hexágonos y heptágonos, con un claro dominio de la geometría hexagonal. La excepción es el sitio “Cristales-Peñón”, donde dominan los tetrágonos (Figura 5).

Figura 5 Diagramas de barras de número promedio de lados, ñ , para siete sitios seleccionados, en los cuales se realizaron medidas detalladas con procesamiento de imágenes. A. Los Ataúdes. B. Carros de piedra. C. Basalt Cay. D. Domo Victoria. E. Cristales. F. Cristales-Negritos. G. Cristales-Peñón. H. Diagrama compuesto por los datos de los siete afloramientos. En cada diagrama se indica el número total, T, de polígonos definidos.
Áreas trasversales, homogeneidad y orden
Los valores de áreas promedio, longitud promedio de lado y ángulos internos promedio de las columnas son parametrizados en forma de una proporción entre la desviación estándar de las medidas y el dato promedio, llamada variación relativa. Por ejemplo, el área de las secciones transversales de las columnas se cuantifica como la relación σ A /Ā, y se denomina variación relativa del área. Luego, los parámetros σ A /Ā, σ L /L¯ , y σ θ /θ¯ son comparados con el índice de hexagonalidad (medida de la madurez) para visualizar posibles dependencias entre estos parámetros y la madurez de la facies columnata de disyunción (Figura 6).
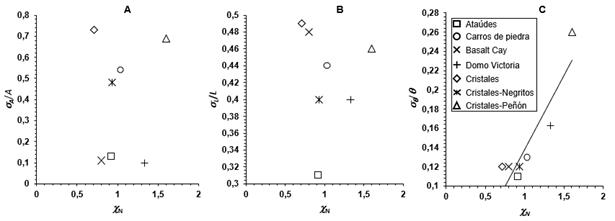
Figura 6 A. Variación relativa del área (σA/Ā) vs hexagonalidad (χN) de las columnas de los afloramientos con facies columnata. B. Variación relativa del promedio de longitudes de lado de las columnas (σL/L¯ ) vs índice de hexagonalidad. C. Variación relativa del ángulo interno de las columnas (σθ/θ¯) vs índice de hexagonalidad. La línea de mejor ajuste en este caso está definida por la función σ /θ¯ = 0,15χ - 0,01, con coeficiente de correlación R = 0,91.
Tamaño de estría (S¯ ) vs longitud de lado (L¯ )
Para estudiar la relación entre los tamaños de estría y la longitud de lado de la cara de la columna, donde aparece la estría, se determinó en primer lugar la relación de los promedios entre estos dos parámetros, η = S ¯/L¯ , para cada uno de los afloramientos. El valor promedio calculado entre todos los sitios es η = 0,15 con desviación estándar de 0,02 (Tabla 2). También se graficaron las alturas de estría (S ¯) vs las longitudes de los lados (L¯ ) para los afloramientos en los cuales fue posible obtener varias mediciones (Figura 7).
Tabla 2 Relación entre los promedios de alturas de estría y longitud promedio de lado de columna, η = S ¯/L¯ , para los afloramientos estudiados.
| Sitio | η = ¯S /¯L |
|---|---|
| Ataúdes | 0,15 |
| Carros de Piedra | 0,14 |
| Basalt Cay | 0,13 |
| Domo Victoria | 0,18 |
| Cristales | 0,13 |
| Cristales-Negritos | 0,11 |
| Cristales-Peñón | 0,19 |

Figura 7 Gráfica de altura de estría, S, vs longitud de lado, L, para los afloramientos con disyunción columnar en Colombia, en los cuales fue posible identificar la facies tipo columnata. La línea de ajuste define la relación S = 0,21L - 1,76, con un coeficiente de regresión R = 0,92.
A modo de comparación, se graficaron los datos promedio de altura de estría (S ¯) y ancho de cara de columna (L¯ ) de las unidades estudiadas en Colombia, junto con los datos de otros afloramientos alrededor del mundo: los basaltos del río Columbia en Norteamérica, lavas basálticas de la isla de Staffa en Escocia y lagos de lava prehistóricos en Hawaii y New Jersey (Estados Unidos), como se muestra en la Figura 8. Los tamaños promedios de estrías son proporcionales a los promedios de ancho de cara de columna, y, para los sitios estudiados en Colombia, las estrías son aproximadamente el 10-25% del ancho de cara de columna, rango consistente con la mayoría de observaciones en otros sitios a nivel mundial.

Figura 8 Gráfica de altura promedio de estrías vs longitud promedio de lado de columna para diferentes macizos rocosos alrededor del mundo. CRB-1: Columbia River Basalts (Grossenbacher y McDuffie, 1995); CRB-2 Columbia River Basalts (Goehring, 2008); SIE: Staffa Island-Escocia (Phillips et al., 2013); BPH: Boiling Pots-Hawaii, 1WB: 1st Watchung Basalt-New Jersey, PMLL: Prehistoric Makaopuhi Lava Lake-Hawaii (Ryan y Sammis, 1981). Las líneas marcadas como 5%, 10%, 20% y 35% representan las relaciones S¯=PL¯ , donde P = 0,05, 0,10, 0,25 y 0,35, respectivamente.
Números de Péclet
Siguiendo a Goehring (2008) , se calcularon los valores del número de Péclet (P e ) de las disyunciones columnares estudiadas en siete sitios en Colombia, utilizando la ecuación 8 y los datos de la Tabla 2. Los valores de P e están en el rango 0,28-0,41, con valor promedio de 0,32 y desviación estándar de 0,06.
Discusión
La disyunción columnar es un fenómeno común en rocas volcánicas y depósitos volcaniclásticos soldados; en Colombia, se han documentado múltiples sitios en los cuales se realizaron observaciones generales de campo y análisis detallados utilizando programas de análisis de imágenes. La inspección visual de los afloramientos analizados en este estudio revela que, en vista de planta, el patrón geométrico de las uniones entre diaclasas tiende a organizarse principalmente en polígonos de cinco y seis lados, aunque también se notan otras geometrías de orden menor (tetrágonos) y mayor (heptágonos). Una comparación gráfica de los arreglos poligonales de la disyunción columnar en Colombia se muestra en la Figura 2, y los datos se resumen en la Tabla 1.
De los afloramientos que exhiben tendencia a la organización hexagonal óptima (N=6), todos corresponden a emplazamientos de lava, de los cuales los que muestran la distribución poligonal más uniforme son los ubicados en Basalt Cay (al norte del archipiélago de San Andrés, Providencia y Santa Catalina), que han sido clasificados como dacitas neógenas (Álvarez-Gutiérrez et al., 2014), y los Carros de Piedra de edad Neógeno tardío- Cuaternario temprano en el municipio de Casabianca, Tolima (Barrero y Vesga, 1976; Ceballos-Hernández et al., 2020). Los dos afloramientos de depósitos de CDP con disyunción documentados (Distrito de Riego de Nátaga, Huila y Puente “Ricardo Chica”-Herveo, Tolima) tienden a una organización de orden menor en pentágonos y tetrágonos, respectivamente. Las rocas del Distrito de Riego de Nátaga corresponden a tobas (ignimbritas) jurásicas de la Formación Saldaña (Marquínez et al., 2002, 2006), mientras que en el sitio Puente “Ricardo Chica” de Herveo afloran rocas del Plioceno-Holoceno formadas por depósitos de flujos de bloques y ceniza soldados del volcán Cerro Bravo (Méndez-Fajury, 1989; Monsalve, 1991; Cepeda, 2000; Alarcón et al.,2020).
Hetényi et al. (2012) midieron el tamaño de columnas en cincuenta sitios en tres países de Europa, y dedujeron condiciones de contorno para el proceso de enfriamiento y la tasa de pérdida de calor. Hofmann et al. (2015) , mediante la aplicación de conceptos de la mecánica de fractura elástica lineal y el principio de máxima tasa de liberación de energía, describieron la evolución del patrón de fisuras como una transición de la configuración rectangular inicial al patrón hexagonal. Mediante un estudio analítico, y por medio de la simulación tridimensional de elementos finitos, Christensen et al. (2016) presentaron un estudio exhaustivo de disyunción columnar, basado en experimentos de enfriamiento de ácido esteárico, y utilizaron simulaciones numéricas para demostrar que el diámetro de las disyunciones columnares es una función no trivial.
Grado de madurez, homogeneidad y orden
La madurez de la disyunción para siete sitios, medida a partir del índice de hexagonalidad, está en el rango 0,71-1,6, y la variación en los tamaños de los polígonos, que indica el grado de homogeneidad, está en el rango 0,1-0,73. Los datos indican que el afloramiento Cristales presenta el mayor grado de madurez, representado en el menor valor del índice χN =0,71 (Figura 6A). A su vez, la variación relativa de área de sus columnas  indica que este afloramiento es el menos homogéneo de todos los sitios estudiados. En contraste, el afloramiento Domo Victoria tiene muy baja madurez (aunque no la más baja, χ
N
=1,33) y el mayor grado de homogeneidad, ya que para este sitio
indica que este afloramiento es el menos homogéneo de todos los sitios estudiados. En contraste, el afloramiento Domo Victoria tiene muy baja madurez (aunque no la más baja, χ
N
=1,33) y el mayor grado de homogeneidad, ya que para este sitio 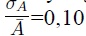 A pesar de lo que muestran estos datos extremos, no puede asegurarse que exista una relación inversa clara entre la madurez y el grado de homogeneidad de las columnas, ya que los datos en conjunto no presentan dicha tendencia (Figura 6 A ).
A pesar de lo que muestran estos datos extremos, no puede asegurarse que exista una relación inversa clara entre la madurez y el grado de homogeneidad de las columnas, ya que los datos en conjunto no presentan dicha tendencia (Figura 6 A ).
A nivel más local, los sitios Cristales, Cristales- Negritos y Cristales-Peñón presentan grados de madurez y homogeneidad en los rangos 0,71-1,6 y 0,48-0,73, respectivamente, dispersión que llama la atención, ya que los tres sitios son cercanos y todos pertenecen a emplazamientos de lava del período eruptivo Pre-Ruiz (Ceballos-Hernández et al., 2020). Se asume que factores externos como la meteorización o la intervención antrópica pueden afectar la forma de las columnas, y han actuado de manera uniforme en estos tres sitios a lo largo del tiempo; la dispersión en la madurez y la homogeneidad señalan condiciones particulares diferentes durante el emplazamiento de cada flujo de lava.
El grado de ordenamiento se estimó mediante el análisis de los parámetros de variación relativa de longitud de lado,  , y la variación relativa de ángulo interno, Estos parámetros están en los rangos 0,31- 0,49 y 0,11- 0,26, respectivamente. De los datos de las Figuras 6 B y 6C se infiere que el más ordenado es el afloramiento Los Ataúdes, que presenta la menor variación relativa de longitud de lado,
, y la variación relativa de ángulo interno, Estos parámetros están en los rangos 0,31- 0,49 y 0,11- 0,26, respectivamente. De los datos de las Figuras 6 B y 6C se infiere que el más ordenado es el afloramiento Los Ataúdes, que presenta la menor variación relativa de longitud de lado,  , y también el menor valor de variación relativa de ángulo
, y también el menor valor de variación relativa de ángulo  . Por su parte, el menos ordenado tiende a ser el afloramiento Cristales-Peñón, donde también se determinan el menor grado de madurez de todos los sitios analizados y una baja homogeneidad.
. Por su parte, el menos ordenado tiende a ser el afloramiento Cristales-Peñón, donde también se determinan el menor grado de madurez de todos los sitios analizados y una baja homogeneidad.
Al promediar las variaciones relativas de σL entre los sitios, se obtiene un valor de 0,35, con una desviación estándar de 0,09. Para comparar este valor con los reportados en otras publicaciones, se promediaron los valores  para los sitios: isla de Staffa (Phillips et al., 2013); algunos sitios de Francia, Hungría e Islandia, registrados por Hetényi et al. (2012) ; el grupo de basaltos del río Columbia en Norteamérica, tomados por Goehring (2008) ; Monte Mudeung en Corea del sur (Lim et al., 2015); y el este y sureste de China, publicados por Li y Liu (2020). Se obtuvo un valor de 0,34 con una desviación estándar de 0,08. Estos dos promedios, el mundial y el de siete sitios en Colombia, se correlacionan bien con los datos experimentales de desecación de fécula de maíz (Goehring y Morris, 2005). Lo anterior reafirma la hipótesis del desorden residual inherente del fenómeno de disyunción columnar, que se presenta a diferentes escalas de longitud y en distintos materiales, es decir, el grado de desorden de un patrón formado por las disyunciones columnares no depende significativamente del proceso físico que lleva a la contracción del material, sino de la naturaleza misma del sistema no lineal.
para los sitios: isla de Staffa (Phillips et al., 2013); algunos sitios de Francia, Hungría e Islandia, registrados por Hetényi et al. (2012) ; el grupo de basaltos del río Columbia en Norteamérica, tomados por Goehring (2008) ; Monte Mudeung en Corea del sur (Lim et al., 2015); y el este y sureste de China, publicados por Li y Liu (2020). Se obtuvo un valor de 0,34 con una desviación estándar de 0,08. Estos dos promedios, el mundial y el de siete sitios en Colombia, se correlacionan bien con los datos experimentales de desecación de fécula de maíz (Goehring y Morris, 2005). Lo anterior reafirma la hipótesis del desorden residual inherente del fenómeno de disyunción columnar, que se presenta a diferentes escalas de longitud y en distintos materiales, es decir, el grado de desorden de un patrón formado por las disyunciones columnares no depende significativamente del proceso físico que lleva a la contracción del material, sino de la naturaleza misma del sistema no lineal.
Por otro lado, a partir de dos perspectivas diferentes, se observó que el número de lados de polígonos en la mayoría de sitios analizados en Colombia tiende a ñ =6, y, como es de esperarse, la distribución de los ángulos internos medidos es similar entre la mayoría de los casos, agrupándose alrededor de 120°. La excepción, nuevamente, es el sitio Cristales-Peñón, donde los polígonos tienden a tener cuatro lados (Figura 5). También se encuentra que la variación relativa de los ángulos internos,  , es baja para la mayoría de los afloramientos estudiados (Figura 6 C ). En comparación con las estadísticas de polígonos en columnas en fécula de maíz desecada (Goehring y Morris, 2005), y las medidas de los ángulos de la famosa Figura 2.8 de O’Reilly (1879) de la Calzada del Gigante, se puede decir que la mayoría de estructuras de disyunción en Colombia están en el mismo rango. El afloramiento de Cristales-Peñón destaca por discrepar respecto a valores de hexagonalidad comunes en Colombia y alrededor del mundo. Sus bajos grados de homogeneidad y orden, sumados a la baja madurez, señalan lavas cuyos patrones de disyunción fueron atrofiados, quizá por condiciones locales que dominaron durante el emplazamiento.
, es baja para la mayoría de los afloramientos estudiados (Figura 6 C ). En comparación con las estadísticas de polígonos en columnas en fécula de maíz desecada (Goehring y Morris, 2005), y las medidas de los ángulos de la famosa Figura 2.8 de O’Reilly (1879) de la Calzada del Gigante, se puede decir que la mayoría de estructuras de disyunción en Colombia están en el mismo rango. El afloramiento de Cristales-Peñón destaca por discrepar respecto a valores de hexagonalidad comunes en Colombia y alrededor del mundo. Sus bajos grados de homogeneidad y orden, sumados a la baja madurez, señalan lavas cuyos patrones de disyunción fueron atrofiados, quizá por condiciones locales que dominaron durante el emplazamiento.
En lo que respecta a los valores de χN y  de los afloramientos, se encontró una correlación positiva (Figura 6 C ), lo cual era de esperarse porque la suma de los ángulos internos de un polígono aumenta con el número de lados (para un tetrágono la suma es 360°, mientras que para un hexágono es 720°), y, por tanto, las disyunciones que formen columnas con más caras laterales deben tener un ángulo interno promedio más alto. Similarmente, los patrones de disyunción que exhiban alto valor de índice de hexagonalidad tendrán una mayor dispersión de ángulos internos, como el caso del afloramiento Cristales-Peñón.
de los afloramientos, se encontró una correlación positiva (Figura 6 C ), lo cual era de esperarse porque la suma de los ángulos internos de un polígono aumenta con el número de lados (para un tetrágono la suma es 360°, mientras que para un hexágono es 720°), y, por tanto, las disyunciones que formen columnas con más caras laterales deben tener un ángulo interno promedio más alto. Similarmente, los patrones de disyunción que exhiban alto valor de índice de hexagonalidad tendrán una mayor dispersión de ángulos internos, como el caso del afloramiento Cristales-Peñón.
Relación entre el tamaño de estría (S¯ ) vs longitud de lado (L¯ )
En la Figura 7 se puede apreciar que, entre los siete sitios representados, los datos que presentan menor dispersión son los correspondientes a Cristales, Los Ataúdes y Domo Victoria. También se revela que el ajuste lineal por mínimos cuadrados indica correlación positiva entre el tamaño de las estrías y la longitud de lado de las columnas, con coeficiente de regresión R= 0,92. Esto comprueba que existe una proporción directa entre el tamaño de estría y el tamaño de lado de las columnas en la disyunción de los afloramientos estudiados en Colombia. En un contexto global, los datos de sitios bien estudiados sugieren que el tamaño de estrías usualmente está entre el 5 y el 20% de la longitud de lado de columna (Basaltos del río Columbia, Grossenbacher y McDuffie, 1995; Goehring, 2008) o entre el 7 y el 20% (Isla Staffa, Phillips et al., 2013). Los datos de Colombia exhiben una variación similar para esta relación, ya que los tamaños de estría estarían comúnmente entre el 10 y el 25% de la longitud de lado de columna (Figura 8). Se ha sugerido que la proporcionalidad entre el tamaño de estrías y la longitud de lado de columnas está relacionada con un control en el proceso de disyunción por parte de las propiedades mecánicas de las rocas (REFs).
Con base en la revisión bibliográfica y en los resultados de este trabajo, se propone que las diferencias encontradas respecto a las dimensiones de estrías y columnas, o la geometría poligonal, estarían relacionadas con la variabilidad de ambientes de formación de las litologías, que implica a su vez variabilidad en composiciones químicas (véase Figuras 4.16 y 4.21 de Calderón, 2021), texturas y condiciones de emplazamiento, o incluso en análisis de diferentes zonas (i. e. facies columnata o entabladura).
Respecto al modo de disipación de calor, las medidas de las estrías y longitudes de columnas en Colombia indican valores bajos de número de Péclet (P e promedio es 0,32), consistentes con regímenes principalmente conductivos. Estos valores deben ser tomados con precaución, ya que provienen de datos de diversos sitios, formados en diferentes tiempos, lo que implica una probabilidad de heterogeneidad en lo relacionado con las condiciones de emplazamiento de las lavas y depósitos de CDP. No debe descartarse la participación del mecanismo de convección asistida por fluidos (agua) en grietas primarias, y es recomendable documentar más afloramientos, principalmente aquellos bien preservados, con similares características geológicas, y en los cuales sea posible establecer con mayor claridad el tipo de facies de disyunción, así como su posición dentro de una unidad particular de flujo. La investigación realizada constituye una primera aproximación al problema de los mecanismos físicos que operan en el emplazamiento de lavas y corrientes de densidad piroclástica en Colombia, y queda por delante un largo camino de exploración de sitios y de aprendizaje.
Conclusiones
El análisis de los datos de geometría y dimensiones de las columnas en múltiples sitios con disyunción en Colombia permite concluir que hay buena coincidencia entre la inspección visual de afloramientos y el análisis utilizando programa de procesamiento de imágenes, por lo que las observaciones en campo pueden ser una aproximación preliminar a rasgos como la madurez, la homogeneidad y el orden de la disyunción columnar. Asimismo, los afloramientos de lava tienen más tendencia a la madurez (n¯ →6) que los afloramientos de DCDP (n¯ →4-5).
De todos los sitios analizados, el afloramiento Cristales, en el flanco suroriental del volcán Nevado del Ruiz, es el más maduro (χ
N
=0,71); el Domo Victoria, un volcán monogenético en cercanías a Manizales, es el más homogéneo  mientras que el sitio Los Ataúdes, en un flujo de lava basáltica, cerca al municipio de Vijes, es el más ordenado
mientras que el sitio Los Ataúdes, en un flujo de lava basáltica, cerca al municipio de Vijes, es el más ordenado  y
y  .
.
Entre los afloramientos de lavas en Colombia, se verifica un desorden residual inherente del fenómeno de disyunción columnar que se cumple para diferentes escalas de longitud y distintos materiales.
Para siete sitios en Colombia, el tamaño de las estrías usualmente es el 10-25% de la longitud de lado de columna, relación que concuerda con resultados de sitios clásicos estudiados en otras partes del mundo.
Los números de Péclet para los afloramientos estudiados están en el rango 0,28-0,41, con promedio de 0,32, valor que también concuerda con el resultado para la disyunción columnar de las lavas del río Columbia en Norteamérica y de los procesos de desecación de agua en almidón (Goehring et al., 2006).