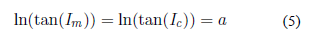Introducción
Las reconstrucciones paleogeográficas y los modelos tectónicos utilizan técnicas como el paleomagnetismo, debido a que aporta información clave como rotaciones o variaciones latitudinales (Butler, 1992; Garcés et al., 1996a). A su vez, el paleomagnetismo se basa en que el campo magnético terrestre es aproximado al dipolo axial geocéntrico, donde el campo es producido por un único dipolo magnético en el centro del planeta y alineado con su eje de rotación. Este modelo permite determinar, basado en los datos de inclinación magnética, los valores de latitud usando la relación tan I = 2tan A (Butler, 1992). Sin embargo, diferentes estudios paleomagnéticos han demostrado que el valor de la inclinación medida podría tener un aplanamiento por compactación de sedimentos (King, 1955; Deamer y Kodama, 1990; Kodama, 1997), y por tanto determinar este aplanamiento es necesario para validar las reconstrucciones paleomagnéticas y los modelos tectónicos (Kodama, 2012; Li y Kodama, 2016). El aplanamiento de la inclinación magnética es calculado usando la relación (King, 1955):
Donde f es el factor de aplanamiento, I m es la inclinación medida e I c es la inclinación corregida. El factor de aplanamiento f varía de 1,0 (sin aplanamiento) a 0 (aplanamiento máximo) (nótese que esto se cumple solo en los casos en que l m ≤ I c ).
Dado que las rocas ígneas no sufren compactación debido al enfriamiento o cementación rápida, un método simple para detectar la existencia del aplanamiento de la inclinación en rocas sedimentarias siliciclásticas consiste es comparar sus valores de inclinación con el valor medido en rocas ígneas (Kodama, 2012; Li y Kodama, 2016).
Existen diferentes aproximaciones para determinar la corrección de la inclinación (Kodama, 2012; Li y Kodama, 2016). Para Kodama (2012) al menos tres procedimientos son utilizados para determinar el factor de aplanamiento y corrección de la inclinación en rocas sedimentarias: Primero, el uso de la anisotropía de remanencia, la cual se usa como procedimiento para calcular el grado de aplanamiento y tiene influencia en el cálculo de paleolatitudes. En este caso la anisotropía de remanencia es función de la anisotropía magnética del grano individual (Kodama, 1997). Esta no es una técnica rutinaria y requiere un enfoque técnico específico para su medición, en el cual la anisotropía del grano individual debe ser determinada secando una mezcla de material magnético y epoxi, bajo un campo magnético entre 35 a 50 mT. Adicionalmente, el material disgregado es llevado al laboratorio de compactación (Kodama, 1997). Segundo, el método Inclinación-Elongación (I-E) (Tauxe et al., 2008), en el cual se calcula el aplanamiento basado en las direcciones magnéticas de periodos prolongados de tiempo, así como las direcciones causadas por la variación secular, por tanto, se requiere un número de datos de inclinación magnética superior a 100. Jiménez et al. (2021) sugieren que el método de I-E (Tauxe et al., 2008), para un conjunto de datos de inclinación menor a 100, induce a sobreestimaciones en la corrección. Por esto, los autores proponen una corrección empírica basada en los valores de corrección promedios reportados en rocas sedimentarias y sugieren un valor de corrección 0,6 para datos en rocas sedimentarias del Grupo Girón en la Cordillera Oriental. Tercero, y de acuerdo con Garcés et al. (1996a), el factor de aplanamiento puede ser determinado usando valores de inclinación y el grado de anisotropía P', derivado del análisis de anisotropía de la susceptibilidad magnética; en este caso el valor de corrección es dependiente de la litología y su ambiente de depósito.
En el presente trabajo se pretende realizar el cálculo del aplanamiento de la inclinación magnética a partir del método descrito, utilizando un nuevo conjunto de datos de ASM y la disponibilidad de datos de inclinaciones y ASM reportadas en rocas del Triásico al Mioceno de la Cordillera Oriental. El cálculo del aplanamiento de la inclinación magnética es útil para evaluar y ajustar los modelos tectónicos de la margen NW de Suramérica.
Paleomagnetismo y anisotropía de la susceptibilidad magnética en la Cordillera Oriental
Los primeros trabajos de paleomagnetismo en los Andes del Norte están concentrados en el área de Bucaramanga, Macizo de Santander y Serranía de Perijá (Creer et al., 1970; Hargraves et al., 1984; Maze y Hargraves, 1984) (Figura 1). Los trabajos más recientes de paleomagnetismo se han enfocado en rocas del Jurásico, Cretácico y Cenozoico de la Cordillera Oriental (Bayona et al., 2006; Jiménez et al., 2014, 2015, 2021, 2022; García y Jiménez, 2016), Andes de Mérida (Castillo et al., 1991) y Serranía de Perijá (Gose et al., 2003; Nova et al., 2012) (Figura 1). Con base en datos paleomagnéticos de unidades del Jurásico Inferior, sin considerar un posible aplanamiento de la inclinación, Bayona et al. (2006) sugieren una traslación de bloques desde latitudes del hemisferio sur ~10°S. Por otro lado, las rocas del Jurásico Superior a Cretácico Inferior estarían localizadas en latitudes cercanas al ecuador (Bayona et al., 2006). Bayona et al. (2006) reportan rotaciones antihorarias mayores a 90° relacionadas con la Falla de Bucaramanga.

Figura 1 Mapa con las principales estructuras y límites estructurales de la Cordillera Oriental (CO), Macizo de Santander (MS), Andes de Mérida, Perijá (P) y Sierra Nevada de Santa Marta (SNSM). El recuadro rojo enmarca la localización de la sección estratigráfica del Grupo Girón (Figura 2).
Con base en un estudio magnetoestratigráfico, Jiménez et al. (2021) siguen la nomenclatura estratigráfica de Etayo-Serna (1989) en una sección del Grupo Girón en el Anticlinorio de Los Yariguíes, y sugieren una edad para el Grupo Girón entre Kimmeridgiano y Valanginiano. Con base en un factor de corrección de 0,6, Jiménez et al. (2021, 2022) sugieren que las rocas del Jurásico Superior han tenido una posición cercana a la posición actual ~7° y reportan rotaciones horarias de ~50°, relacionadas a fallas transversales NE. Basado en datos paleomagnéticos y anisotropía de la susceptibilidad magnética, Jiménez et al. (2014) sugieren que la Cordillera Oriental es un orógeno primario que no ha experimentado rotaciones significativas y que es producto de la partición de la deformación, con desplazamientos de rumbo destral en la zona axial y cizalla pura en los flancos. En el eje de la Cordillera Oriental, García y Jiménez (2016) reportan rotaciones horarias y antihorarias de magnitud moderada asociadas a desplazamientos de rumbo.
Las lineaciones magnéticas inclinadas reportadas en la Cordillera Oriental son el resultado de la deformación no coaxial que ha experimentado la Cordillera (Jiménez et al., 2014). García y Jiménez (2016) reportan lineaciones magnéticas paralelas a la tendencia estructural de la Cordillera Oriental y la preservación de fábricas sedimentarias.
Sin evaluar el posible aplanamiento de la inclinación, los trabajos paleomagnéticos en la Serranía de Perijá (Gose et al., 2003; Nova et al., 2012) y en los Andes de Mérida (Castillo et al., 1991) proponen que las rocas del Jurásico Medio al Cretácico Inferior no han sufrido un movimiento latitudinal significativo. En la Serranía de Perijá se reportan rotaciones horarias cercanas ~ 50° (Gose et al., 2003; Nova et al., 2012).
Respecto a la mineralogía magnética, con base en experimentos de magnetismo remanente isotermal (IRM), el IRM y su desmagnetización progresiva o las curvas termomagnéticas, los trabajos reportados en la Cordillera Oriental (Bayona et al., 2006; Jiménez et al., 2014, 2015, 2021, 2022; García y Jiménez, 2016; Jiménez y García, 2023), los Andes de Mérida (Castillo et al., 1991) y la Serranía de Perijá (Gose et al., 2003; Nova et al., 2012) reportan la presencia de hematita como principal portador del magnetismo remante natural. Los valores bajos de susceptibilidad (< 200 x 10-6 SI) sugieren un aporte de minerales paramagnéticos contenidos en la matriz arcillosa (Jiménez et al., 2014, 2022).
Metodología
Anisotropía de la susceptibilidad magnética
El comportamiento magnético de una roca está condicionado por su mineralogía y por el campo magnético terrestre. En un cuerpo rocoso, la sensibilidad a la magnetización está definida por una constante adimensional llamada susceptibilidad magnética (X):
Donde M es la magnetización de la muestra y H, el campo magnético aplicado. La susceptibilidad magnética (X) será positiva si la mineralogía dominante es ferromagnética (s.l) y paramagnética, o será negativa si la mineralogía dominante es diamagnética. En un volumen de roca, las direcciones preferenciales de una propiedad física en 3 ejes determinan una fábrica o anisotropía (Tarling y Hrouda, 1993).
De acuerdo con Caballero (2011), una fábrica o una anisotropía de una roca es un arreglo espacial de sus constituyentes y determina la distribución de sus propiedades físicas (e.g. susceptibilidad magnética). Por tanto, existen diferentes tipos de anisotropías que se originan en una roca debido a la orientación preferencial de sus elementos o constituyentes. En el caso de una roca sedimentaria, el arreglo interno de sus constituyentes estará principalmente asociado a procesos de sedimentación, y la fábrica será primaria o sedimentaria. Si la orientación preferencial está afectada por procesos de deformación, la fábrica será tectónica y definida por lineaciones o foliaciones; si la fábrica está definida por los constituyentes ferromagnéticos (s.l), será una fábrica de remanencia (Tarling y Hrouda, 1993; Caballero, 2011).
Según Tarling y Hrouda (1993), la anisotropía de la susceptibilidad magnética (ASM) puede ser definida como un tensor simétrico de segundo orden, cuya magnitud y orientación de sus ejes principales están definidas por K 1 , K2 y K3 (K 1 >K 2 >K3). La ASM será gráficamente representada por un elipsoide, donde K1,=Kmax, K2 = Kint y K3 = K min . (Hrouda, 1982; Borradaile, 1988). Los resultados son usualmente procesados usando el software libre Anisoft de AGICO, donde se obtienen la orientación y la magnitud de los tres ejes principales del elipsoide de ASM, y con los cuales se obtienen diferentes paramentos con sentido geológico (Jelinek, 1981; Tarling y Hrouda, 1993). Los principales parámetros son: valor medio de la susceptibilidad, K m = (K1 + K2 + K3) /3 (SI). El eje máximo (K1) y el eje mínimo (K 3 ) del elipsoide de la ASM que corresponden a la lineación magnética y el polo de la estratificación, respectivamente. El parámetro de forma del elipsoide de la ASM (T). T = 2(ln K2 - ln K3)/(ln K1 - ln K3); si T > 0, el elipsoide es oblado y si T < 0, el elipsoide es prolado. El grado de anisotropía del elipsoide de ASM (P'). P' = exp (2 [(ln K1 - ln Km)2 + (ln K2 - ln Km)2 + (ln K3 - ln Km)2])1/2. Finalmente, la lineación magnética (L) es definida por la relación L = K1/K2, y la foliación magnética (F) es definida como F = K2/K3.
Cálculo de aplanamiento y corrección de la inclinación magnética
La relación entre la sedimentación, direcciones de remanencia magnética y fábricas magnéticas ha sido estudiada por diferentes autores (Hrouda, 1982; Jackson et al., 1991; Kodama, 1997, 2009, 2012; Tan y Kodama, 2002; Gilder et al., 2003). Debido a que el aspecto más complicado en la corrección de la inclinación por aplanamiento en rocas hematíticas es la determinación de la anisotropía de la partícula individual, Kodama (2009) sugiere usar valores cercanos a 1,4-1,45 para evitar las complejidades de las mediciones. Según Gilder et al. (2003), la compactación induce al aplanamiento de la inclinación y podría causar que el grado de anisotropía (P') se incremente, por tanto, la fábrica oblada (T > 0) tendría más aplanamiento que la fábrica prolada (T < 0). Según Garcés et al. (1996b), la fábrica magnética dominada por minerales paramagnéticos se correlaciona con el aplanamiento de la inclinación según el tipo de roca determinado. Garcés et al. (1996a) sugiere que las aproximaciones teóricas (Jackson et al., 1991) no pueden ser aplicadas a sedimentos naturales, aunque podrían ser aplicados solo con una simplificación, como lo sugieren Collombat et al. (1993), en sedimentos marinos. En los dos casos teórico (Jackson et al., 1991) y aplicado (Collombat et al., 1993), el factor de aplanamiento f es determinado por la relación entre la dirección paleomagnética y la anisotropía de remanencia.
Para Garcés et al. (1996a), una misma correlación se puede lograr usando la anisotropía de la susceptibilidad magnética, ya que se estaría midiendo los mismos parámetros. Esta aproximación podría ser viable si todos los constituyentes magnéticos formaran una misma fábrica magnética. García-Lasanta et al. (2015) muestran que a baja temperatura y a temperatura ambiente la fábrica magnética no varía considerablemente, ya que los filosilicatos y la hematita tienen una anisotropía de susceptibilidad magnética muy oblata, como lo sugieren Martín-Hernández y Hirt (2003).
De acuerdo con Garcés et al. (1996a), una medida del alineamiento de las partículas en los sedimentos puede ser determinada usando los parámetros de grado de anisotropía P' y el parámetro de forma T, teniendo en cuenta que cada facies tendrá un rango de P' o T particular, es decir, cada litología tendrá un elipsoide particular. La inclinación tiene una fuerte relación con el elipsoide de ASM, y se infiere una correlación lineal positiva entre el ln (P') y ln (tan(I)).
La metodología utilizada por Garcés et al. (1996a) se basa en la definición del factor de aplanamiento como (ASM2/ASMx)b, de acuerdo con Collombat et al. (1993), y asume que el eje de mínima susceptibilidad de los elipsoides ASM (K 3 ) es perpendicular a la estratificación, entonces:
Donde I m es la inclinación medida, I c es la inclinación corregida, P' es el grado de anisotropía y b es una constante. La misma ecuación puede escribirse como:
Donde Y = ln(tan(Im)), X = -ln(P') y α = ln(tan(Ic)). Esta ecuación se ajusta a la media estimada del grado de anisotropía y a la inclinación medida en cada muestra/ sitio para obtener los valores de a y b. Si se asume el caso de una roca perfectamente isotrópica con un P' = 1, no se presentaría un error en la inclinación, por lo que:
Siendo posible obtener la inclinación corregida (Garcés et al., 1996a). El ajuste de la ecuación se realiza mediante la librería scipy de Python, específicamente con la herramienta curve fit (scipy.optimize.curve fit - SciPy v1.7.1 Manual), la cual permite obtener los parámetros a y b a partir del ajuste de la ecuación 4 y de los datos requeridos (P' e I m ).
Distribución de datos de paleomagnetismo y susceptibilidad magnética en la Cordillera Oriental
En los estudios de paleomagnetismo y anisotropía de la susceptibilidad magnética en rocas detríticas en la Cordillera Oriental (Figura 1), el muestreo se realiza en lodolitas y areniscas de grano fino, por tanto, el aporte a la susceptibilidad magnética será en su mayoría por minerales paramagnéticos como arcillas y filosilicatos (Jiménez et al., 2014, 2022). En la Cordillera Oriental se dispone de un conjunto de datos de declinación (D) e inclinación (I) magnética y datos del grado de anisotropía de la susceptibilidad magnética, distribuidos en unidades sedimentarias del Triásico-Jurásico al Cretácico Inferior (Jiménez et al., 2014, 2022) y del Cretácico Inferior al Mioceno (Jiménez et al., 2014; García y Jiménez, 2016) (Figura 1, Tabla Suplementaria 1 y Tabla Suplementaria 2). Otro conjunto de datos disponibles de declinación e inclinación magnética corresponde a los reportados por Jiménez et al. (2021), correspondientes a la sección estratigráfica del Grupo Girón, que corresponde a 199 especímenes con datos (Figura 2, Tabla Suplementaria 1). En la misma sección se dispone de un nuevo conjunto de datos de anisotropía de la susceptibilidad magnética para un número representativo de 63 muestras (Figura 1 y Tabla 1).

Figura 2 Mapa geológico en una zona del flanco oriental del Anticlinorio de Los Yariguíes y localización de la columna estratigráfica del Grupo Girón. Columna estratigráfica generalizada con la ubicación de las 63 muestras analizadas para anisotropía de la susceptibilidad magnética. Modificado de Jiménez et al. (2021).
Tabla 1 Resultados de anisotropía de la susceptibilidad magnética en 63 muestras del Grupo Girón medidas en este trabajo. K m es la susceptibilidad media; L = lineación magnética; F = foliación magnética; P’ = grado de anisotropía corregido; T = parámetro de forma.
| Sitio | Formación | Coordenadas WGS84 | Edad | Buz (°) | K m (× 10-6) | K 1 | K 2 | K 3 | L | F | P’ | T | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Latitud L F P’ T (°Norte) | Longitud (°Oeste) | D (°) | I (°) | D (°) | I (°) | D (°) | I (°) | |||||||||
| LS-120 | 310/74 | 126,9 | 45,4 | 29,7 | 146,1 | 18,1 | 263,1 | 54,2 | 1,0027 | 1,0242 | 1,0270 | 0,7942 | ||||
| LS-119 | 310/74 | 112,1 | 67,6 | 24,2 | 164,5 | 15 | 283,5 | 61 | 1,004 | 1,017 | 1,021 | 0,5997 | ||||
| LS-118 | 310/74 | 106,4 | 49,2 | 15,2 | 147,2 | 27,3 | 293,2 | 58,1 | 1,0274 | 1,0092 | 1,0369 | -0,4950 | ||||
| LS-117 | 310/74 | 91,48 | 246,5 | 10,7 | 340,1 | 18,6 | 128,0 | 68,4 | 1,0163 | 1,0043 | 1,0207 | -0,5762 | ||||
| LS-116 | 310/74 | 76,65 | 344,1 | 55,8 | 79,7 | 3,8 | 172,3 | 34,0 | 1,0840 | 1,1551 | 1,2521 | 0,2822 | ||||
| LS-115 | 310/74 | 93,2 | 219,4 | 5,1 | 127,7 | 18,2 | 324,4 | 71,1 | 1,005 | 1,012 | 1,017 | 0,4001 | ||||
| LS-114 | 310/74 | 96,6 | 27,9 | 16,6 | 123,1 | 16,7 | 255,6 | 66,1 | 1,006 | 1,009 | 1,015 | 0,1714 | ||||
| LS-113 | *295/70 | 111,8 | 334,1 | 26,9 | 72,1 | 15,3 | 188,5 | 58,4 | 1,010 | 1,043 | 1,054 | 0,6113 | ||||
| LS-112 | *295/70 | 80,7 | 47,4 | 9,8 | 141,5 | 22,2 | 295,2 | 65,5 | 1,003 | 1,008 | 1,011 | 0,445 | ||||
| LS-111 | *295/70 | 121,3 | 60 | 22,9 | 160,2 | 22,8 | 290 | 56,7 | 1,004 | 1,008 | 1,012 | 0,3826 | ||||
| LS-110 | *295/70 | 116,3 | 29,6 | 21 | 121,9 | 5,9 | 226,8 | 68,1 | 1,005 | 1,013 | 1,018 | 0,4173 | ||||
| LS-109 | *295/70 | 99,7 | 28 | 22,8 | 297,5 | 1,1 | 204,9 | 67,2 | 1,005 | 1,008 | 1,012 | 0,2788 | ||||
| LS-108 | *295/70 | 85,39 | 70,8 | 37,9 | 337,1 | 4,7 | 241,2 | 51,7 | 1,0015 | 1,0154 | 1,0169 | 0,8253 | ||||
| LS-107 | *295/70 | 120,6 | 74 | 40,8 | 312,2 | 31,5 | 198,5 | 33,3 | 1,105 | 1,256 | 1,389 | 0,3902 | ||||
| LS-106 | Los Santos | 6,84050 | 73,28489 | Jurásico Tardío- Cretácico Temprano | *295/70 | 70,9 | 35,1 | 51,1 | 128,4 | 2,6 | 220,4 | 38,8 | 1,040 | 1,084 | 1,127 | 0,3464 |
| LS-105 | *294/72 | 21,68 | 5,6 | 10,9 | 113,5 | 58,0 | 269,3 | 29,6 | 1,0048 | 1,0179 | 1,0229 | 0,5741 | ||||
| LS-104 | *294/72 | 34,96 | 59,4 | 23,5 | 309,4 | 38,1 | 173,1 | 42,7 | 1,0073 | 1,0784 | 1,0863 | 0,8250 | ||||
| LS-103 | *294/72 | 29,9 | 111,1 | 13,1 | 2,5 | 53,9 | 209,8 | 33 | 1,073 | 1,172 | 1,258 | 0,3833 | ||||
| LS-102 | *294/72 | 16,4 | 64,9 | 39,7 | 323,2 | 13,8 | 218 | 47 | 1,013 | 1,010 | 1,022 | -0,1498 | ||||
| LS-100 | *294/72 | 110,3 | 31,4 | 28,3 | 131,8 | 18,5 | 250,6 | 55,2 | 1,007 | 1,005 | 1,012 | -0,1035 | ||||
| LS-98 | 95/46 | 86,4 | 27,4 | 37,4 | 152,6 | 37 | 269,8 | 31,2 | 1,005 | 1,005 | 1,011 | -0,0101 | ||||
| LS-97 | 95/46 | 78,83 | 47,1 | 26,0 | 155,4 | 32,7 | 286,8 | 45,9 | 1,0090 | 1,0059 | 1,0149 | -0,2086 | ||||
| LS-96 | 95/46 | 102,5 | 42,9 | 29,6 | 164,4 | 42,6 | 291,1 | 33,1 | 1,012 | 1,003 | 1,015 | -0,5953 | ||||
| LS-95 | 95/46 | 69,3 | 22,5 | 38,8 | 137 | 27,2 | 251,7 | 39,1 | 1,007 | 1,010 | 1,016 | 0,1987 | ||||
| LS-93 | 95/46 | 87,8 | 342,7 | 2,8 | 76 | 49,5 | 250,3 | 40,3 | 1,017 | 1,020 | 1,038 | 0,0741 | ||||
| LS-92 | 95/46 | 86,2 | 33,6 | 34 | 138,2 | 20,5 | 253,5 | 48,7 | 1,007 | 1,034 | 1,041 | 0,6346 | ||||
| LS-91 | 80/70 | 76,8 | 8,7 | 16,5 | 112,1 | 38 | 260 | 47,3 | 1,010 | 1,024 | 1,034 | 0,3994 | ||||
| LS-90 | 80/70 | 60,99 | 359,4 | 17,3 | 139,6 | 67,9 | 265,1 | 13,3 | 1,0097 | 1,0113 | 1,0211 | 0,0727 | ||||
| LS-89 | 119/44 | 90,5 | 1,6 | 14,3 | 119,4 | 61,3 | 264,9 | 24,3 | 1,006 | 1,011 | 1,017 | 0,2682 | ||||
| GR-192 | 95/63 | 57,5 | 159,7 | 51,3 | 14,4 | 33,4 | 272,5 | 17,3 | 1,0046 | 1,0298 | 1,035 | 0,727 | ||||
| GR-191 | 95/63 | 89,7 | 164,4 | 21,6 | 20,8 | 63,8 | 260,1 | 14,1 | 1,0032 | 1,0234 | 1,027 | 0,759 | ||||
| GR-189 | 95/63 | 86,4 | 153,8 | 22,8 | 31,3 | 52 | 257 | 28,6 | 1,0032 | 1,0192 | 1,022 | 0,712 | ||||
| GR-188 | 95/63 | 39,1 | 183,9 | 22,7 | 19,6 | 66,6 | 276,3 | 5,7 | 1,0105 | 1,0358 | 1,047 | 0,543 | ||||
| GR-187 | 95/63 | 57,68 | 194,3 | 21,1 | 96,9 | 18,6 | 329,0 | 61,3 | 1,0048 | 1,0931 | 1,0983 | 0,8972 | ||||
| GR-186 | 95/63 | 56,5 | 180,3 | 21,4 | 73,5 | 36,5 | 294,1 | 45,7 | 1,005 | 1,0069 | 1,012 | 0,155 | ||||
| GR-185 | 95/63 | 31,84 | 182,4 | 36,4 | 59,1 | 36,7 | 300,5 | 32,6 | 1,0028 | 1,0096 | 1,0125 | 0,5434 | ||||
| GR-184 | 95/63 | 44,3 | 260,5 | 74,4 | 31 | 10,3 | 123,2 | 11,6 | 1,0029 | 1,0068 | 1,01 | 0,394 | ||||
| GR-183 | 95/63 | 124,7 | 355,2 | 37,7 | 162,1 | 51,6 | 260,2 | 6,4 | 1,0028 | 1,0181 | 1,0210 | 0,7276 | ||||
| GR-182 | 95/63 | 84,08 | 345,0 | 37,8 | 244,3 | 13,4 | 138,3 | 49,0 | 1,0057 | 1,0079 | 1,0137 | 0,1607 | ||||
| GR-181 | 97/65 | 47,1 | 347,2 | 8,5 | 92,3 | 60,1 | 252,5 | 28,4 | 1,0144 | 1,0092 | 1,024 | -0,221 | ||||
| GR-180 | 97/65 | 62,8 | 171,5 | 2,3 | 76,8 | 64,6 | 262,6 | 25,3 | 1,004 | 1,0115 | 1,016 | 0,48 | ||||
| GR-179 | 97/65 | 49,79 | 174,5 | 15,8 | 75,3 | 29,6 | 289,0 | 55,7 | 1,0111 | 1,0091 | 1,0203 | -0,0946 | ||||
| GR-178 | 97/65 | 41,5 | 159,5 | 48,7 | 4,5 | 38,5 | 264,2 | 12,6 | 1,0079 | 1,023 | 1,024 | 0,488 | ||||
| GR-177 | 97/65 | 54,38 | 165,5 | 20,7 | 46,4 | 52,1 | 268,2 | 30,2 | 1,0048 | 1,0156 | 1,0204 | 0,5300 | ||||
| GR-175 | 97/65 | 54,6 | 170,1 | 4,9 | 76,4 | 36,3 | 266,6 | 53,2 | 1,0349 | 1,1381 | 1,1778 | 0,5811 | ||||
| GR-174 | Angostura del Río Lebrija | 6,84347 | 73,2982 | Jurásico Tardío | 97/65 | 43,51 | 103,7 | 33,9 | 9,4 | 6,4 | 270,0 | 55,3 | 1,0114 | 1,0033 | 1,0147 | -0,5544 |
| GR-173 | 95/74 | 38,85 | 116,0 | 38,1 | 15,9 | 12,7 | 270,8 | 49,1 | 1,0227 | 1,0108 | 1,0337 | -0,3511 | ||||
| GR-171 | 95/74 | 47,1 | 36,7 | 48,9 | 129,8 | 2,7 | 222,2 | 41 | 1,0107 | 1,0047 | 1,015 | -0,388 | ||||
| GR-170 | 95/74 | 43,69 | 45,1 | 28,6 | 284,7 | 42,8 | 156,5 | 33,7 | 1,0219 | 1,0347 | 1,0574 | 0,2222 | ||||
| GR-169 | 95/74 | 52,9 | 46,5 | 32,4 | 303,5 | 19,6 | 187,6 | 50,8 | 1,0164 | 1,012 | 1,029 | -0,152 | ||||
| GR-168 | 95/77 | 86,3 | 184,5 | 15,5 | 49,6 | 68,6 | 278,6 | 14,4 | 1,005 | 1,0082 | 1,013 | 0,238 | ||||
| GR-167 | 95/74 | 61,43 | 17,5 | 44,0 | 173,1 | 43,3 | 275,2 | 12,5 | 1,0048 | 1,0153 | 1,0201 | 0,5241 | ||||
| GR-166 | 91/77 | 145,9 | 8,7 | 13,1 | 129,1 | 65,2 | 273,7 | 20,6 | 1,0154 | 1,0234 | 1,039 | 0,205 | ||||
| GR-165 | 91/77 | 133,8 | 198,7 | 0,3 | 291,0 | 83,2 | 108,7 | 6,8 | 1,0133 | 1,0501 | 1,0640 | 0,5751 | ||||
| GR-164 | 91/77 | 47,27 | 350,6 | 30,3 | 155,6 | 58,9 | 256,7 | 6,6 | 1,0060 | 1,0282 | 1,0343 | 0,6478 | ||||
| GR-164 | 91/77 | 44,7 | 55,3 | 37,6 | 313,7 | 14,7 | 206,4 | 48,6 | 1,0434 | 1,0345 | 1,079 | -0,112 | ||||
| GR-163 | 91/77 | 55 | 11,7 | 44,2 | 278 | 3,9 | 184 | 45,5 | 1,0382 | 1,1088 | 1,151 | 0,468 | ||||
| GR-162 | 91/77 | 63,7 | 163,1 | 37,6 | 55,8 | 21,1 | 303,2 | 44,9 | 1,0036 | 1,0229 | 1,027 | 0,725 | ||||
| GR-160 | 91/77 | 53 | 273,5 | 27,1 | 30,3 | 41,3 | 161,1 | 36,6 | 1,0155 | 1,0297 | 1,046 | 0,312 | ||||
| GR-159 | 91/77 | 52,15 | 252,9 | 46,3 | 31,9 | 35,8 | 138,5 | 21,6 | 1,0134 | 1,1099 | 1,1247 | 0,7736 | ||||
| GR-158 | 98/80 | 86,4 | 281,3 | 32,9 | 53 | 45,8 | 173 | 25,9 | 1,0153 | 1,1261 | 1,1433 | 0,773 | ||||
| GR-157 | 98/80 | 76,6 | 19,7 | 63 | 224,4 | 24,8 | 129,8 | 9,9 | 1,0135 | 1,0069 | 1,0205 | -0,318 | ||||
| GR-156 | 98/80 | 82,1 | 338,5 | 63,4 | 69 | 0,2 | 159,1 | 26,6 | 1,0217 | 1,0168 | 1,0389 | -0,127 | ||||
Resultados
Anisotropía de la susceptibilidad magnética para el Grupo Girón en la sección de la Cuchilla del Ramo
Se colectaron 63 muestras de lodolitas y areniscas de grano fino del Grupo Girón (Tabla 1) con un taladro portátil a gas y enfriado por agua. Los núcleos fueron orientados in situ mediante una brújula magnética corregida (-7° según el Centro Nacional de Datos Geofísicos, utilizando el Modelo Internacional de Campo Geomagnético (IGFM); http://www.ngdc.noaa.gov/geomag-web/). Los núcleos fueron cortados en muestras estándar de aproximadamente 2,2 cm de longitud y 2,4 cm de diámetro. La medición de la anisotropía de campo bajo se realizó en un Kappabridge multifunción (MFK1-FA, AGICO), utilizando una matriz de 3 posiciones para cada núcleo. El tensor y los parámetros ASM se calcularon a partir de las estadísticas de Jelinek (1978) y fueron procesados en el software libre Anisoft 5.0 usando una proyección del hemisferio inferior, mostrando la orientación de los ejes K1, K2 y K3 (Figura 3).
La susceptibilidad magnética es baja con una susceptibilidad media (Km) de 73,9 x 106 [SI] (Figura 3), lo cual sugiere que la susceptibilidad magnética está dominada por minerales paramagnéticos y que es posible realizar una interpretación basada en la orientación preferencial de los minerales (Rochette, 1987; Rochette et al., 1992; Parés y van der Pluijm, 2002). El elipsoide de anisotropía de susceptibilidad magnética muestra un parámetro de forma T promedio de 0,054 y un grado de anisotropía P' promedio de 1,025. La lineación magnética L y la foliación magnética F promedio son 1,012 y 1,013, respectivamente (Figura 3). El eje K 3 del elipsoide tiende a ubicarse alrededor del polo de la estratificación, lo que sugiere que la forma del elipsoide en general es oblada y conserva su fábrica sedimentaria (Figura 3).

Figura 3 A. Proyección estereográfica (equal-área) del elipsoide de la anisotropía de susceptibilidad magnética. B. Histograma de distribución de la susceptibilidad media (Km). C. Relación entre el grado de anisotropía (P') y la susceptibilidad media (Km). D. Relación entre el parámetro de forma y el grado de anisotropía (P').
Cálculo del factor de aplanamiento en el modelo de referencia
La aplicación del método utilizado por Garcés et al. (1996a) se basa la ecuación 3, por lo que el primer paso consiste en el cálculo de la tangente de la I m y del inverso del grado de anisotropía. Estas son las dos variables de ingreso al modelo curve-fit, que utiliza mínimos cuadrados no lineales para ajustar estos datos a una función dada, que en este caso es el despeje de la tangente de la inclinación medida a partir de las ecuaciones 3 y 4:
Así, usando 1/P' como X, tan(Im) como Y, y (6) como la función de ajuste, curve-fit da como resultado los valores óptimos para los parámetros a y b de tal forma que la suma de los valores residuales es minimizada.
A partir de a y b es posible calcular una tan(Im) modelada para todas las muestras. De la misma forma a es utilizado para calcular la inclinación corregida (Ic) y usando este valor junto con la inclinación medida de cada muestra es posible calcular el factor de aplanamiento (f) a partir de la fórmula:
Donde I c es la inclinación corregida, e I m es la inclinación medida o I DRM . Al obtener un f para cada una de las muestras que quedaron después del filtrado, se da como resultado el promedio de todos los valores de f obtenidos para cada set de datos.
El modelo de referencia corresponde a los datos reportados por Garcés et al. (1996a), que está basado en 11 datos, de los cuales 3 se caracterizan por un alto grado de anisotropía (>1,1), por lo que se descartan (Figura 4). Al aplicar curve fit se obtuvo un ajuste con R2 = 0,9224, α = 0,55 y b = 25,52 y una f de 60,06°, que, al ser comparado con el valor de I c de 60° reportado por Garcés et al. (1996a), indica que la herramienta curve fit funciona correctamente (Figura 4).
4.3 Filtro de datos
Con el fin de unificar los conjuntos de datos por analizar, se realizó un filtro a los datos reportados en la Cordillera Oriental, Catatumbo, Perijá y Sierra Nevada de Santa Marta (Tabla Suplementaria 1 y Tabla Suplementaria 2). El filtro utilizado depende de los valores del grado de anisotropía P', inclinación, aplanamiento y el valor de a95 (parámetro para medir la precisión de las direcciones de magnetización de las rocas; cuanto menor sea, más precisión). Se utilizaron sitios y muestras con un P' < 1,1, inclinación < |20°|, aplanamiento < |15°| y a95 < 20°. El filtro permite utilizar únicamente datos con información de anisotropía de susceptibilidad magnética, por tanto, datos reportados en la Cordillera Oriental, Perijá, Santa Marta (Bayona et al., 2006, 2010; Nova et al., 2012) no pueden incluirse en el modelo. De los 103 datos originales reportados por Jiménez et al. (2014, 2021, 2022) y García y Jiménez (2016) , 68 datos pasaron los 4 filtros, 14 corresponden a sitios de unidades del Triásico-Jurásico Inferior, 43 corresponden al Jurásico Medio-Cretácico Inferior y 11 sitios corresponden a rocas del Cretácico-Cenozoico (Tabla 2).

Figura 4 Ajuste y correlación usando curve fit para el conjunto de datos reportados por Garcés et al. (1996a) según la ecuación y filtrando según los criterios descritos.
Tabla 2 Conjunto de datos utilizados para el modelamiento curvefit. Para el modelo se utilizaron los sitos con datos de inclinación (Im) y el grado de anisotropía (P'). * indica capas volcadas.
| Sitio | Formación | Coordenadas WGS84 | Edad | Fuente | Rumbo/ Buz (°) | Tilt Correct | P' | ||
|---|---|---|---|---|---|---|---|---|---|
| Latitud (° Norte) | Longitud (° Oeste) | D (°) | I m (°) | ||||||
| M04 | Tilatá | 5,530168 | 73,342689 | Mioceno | Jiménez et al., 2014 | 38/26 | 352,5 | 5,7 | 1,019 |
| CP03 | Guaduas | 5,1629 | 73,9972 | Maastrichtiano-Paleoceno | García y Jiménez, 2016 Jiménez et al., 2014 | 202/62 | 5,3 | 10 | 1,044 |
| CP04 | 5,1667 | 74,0000 | *241/75 | 202,3 | 16,1 | 1,024 | |||
| P20 | 4,516292 | 74,146646 | *104/118 | 18,2 | 10,6 | 1,036 | |||
| P131 | 5,559983 | 73,366118 | 106/21 | 12,7 | -0,9 | 1,031 | |||
| P139 | 5,621390 | 72,99559 | 267/53 | 176,9 | 6,8 | 1,023 | |||
| C07 | Chipaque | 5,2201 | 74,0190 | Santoniano | García y Jiménez, 2016 | 349/22 | 192,6 | 4,7 | 1,041 |
| C14 | Rosa Blanca | 5,901171 | 73,334881 | Cretácico Temprano | Jiménez et al., 2014 | 73/4 | 165,1 | -6,6 | 1,02 |
| C122 | San Gil | 6,021040 | 72,957035 | Cretácico Temprano | Jiménez et al., 2014 | 300/25 | 3,9 | -6,6 | 1,023 |
| C123 | 6,021034 | 72,957042 | 300/25 | 347,7 | -3,3 | 1,051 | |||
| LS-119 | Los Santos | 6,840503 | 73,28489 | Jurásico Tardío-Cretácico Temprano | Jiménez et al., 2021 | 310/74 | 218,2 | -0,1 | 1,021 |
| LS-115 | 6,840503 | 73,28489 | 310/74 | 181,6 | -17 | 1,017 | |||
| LS-114 | 6,840503 | 73,28489 | 310/74 | 48,4 | -3,5 | 1,015 | |||
| LS-113 | 6,840503 | 73,28489 | *295/70 | 54,6 | 10,6 | 1,054 | |||
| LS-112 | 6,840503 | 73,28489 | *295/70 | 43,4 | 10,4 | 1,011 | |||
| LS-111 | 6,840503 | 73,28489 | *295/70 | 53,9 | 3,7 | 1,012 | |||
| LS-110 | 6,840503 | 73,28489 | *295/70 | 192,5 | -8,3 | 1,018 | |||
| LS-109 | 6,840503 | 73,28489 | *295/70 | 198,5 | -5,9 | 1,012 | |||
| LS-102 | 6,840503 | 73,28489 | *294/72 | 195,6 | -10,7 | 1,022 | |||
| LS-100 | 6,840503 | 73,28489 | *294/72 | 50 | 14,4 | 1,012 | |||
| LS-98 | 6,840503 | 73,28489 | 95/46 | 69,9 | 14,5 | 1,011 | |||
| LS-96 | 6,840503 | 73,28489 | 95/46 | 38 | -3,1 | 1,015 | |||
| LS-95 | 6,840503 | 73,28489 | 95/46 | 43,7 | 6,5 | 1,016 | |||
| LS-93 | 6,840503 | 73,28489 | 95/46 | 67,5 | 9,9 | 1,038 | |||
| LS-92 | 6,840503 | 73,28489 | 95/46 | 68,4 | -0,6 | 1,041 | |||
| LS-91 | 6,840503 | 73,28489 | 80/70 | 61,9 | 10,7 | 1,034 | |||
| GR-192 | 6,84347 | 73,2982 | 95/63 | 210,7 | -4,8 | 1,035 | |||
| GR-191 | Angostura del Río Lebrija | 6,84347 | 73,2982 | Jurásico Tardío | Jiménez et al., 2021 | 95/63 | 29,6 | -10,6 | 1,027 |
| GR-189 | 6,84347 | 73,2982 | 95/63 | 187,8 | 4,1 | 1,022 | |||
| GR-188 | 6,84347 | 73,2982 | 95/63 | 209,8 | -4,5 | 1,047 | |||
| GR-186 | 6,84347 | 73,2982 | 95/63 | 7,4 | -9,3 | 1,012 | |||
| GR-184 | 6,84347 | 73,2982 | 95/63 | 191,4 | 45,9 | 1,01 | |||
| GR-181 | 6,84347 | 73,2982 | 97/65 | 55,3 | 31,2 | 1,024 | |||
| GR-180 | 6,84347 | 73,2982 | 97/65 | 43,9 | 2,8 | 1,016 | |||
| GR-178 | 6,84347 | 73,2982 | 97/65 | 228,8 | -7,2 | 1,024 | |||
| GR-168 | 6,84347 | 73,2982 | 95/77 | 26,3 | -6,2 | 1,013 | |||
| GR-166 | 6,84347 | 73,2982 | 91/77 | 15,7 | -16 | 1,039 | |||
| GR-164 | 6,84347 | 73,2982 | 91/77 | 42 | -14,8 | 1,079 | |||
| GR-162 | 6,84347 | 73,2982 | 91/77 | 22,9 | 17,1 | 1,027 | |||
| GR-160 | 6,84347 | 73,2982 | 91/77 | 36,9 | -2,4 | 1,046 | |||
| GR-157 | 6,84347 | 73,2982 | 98/80 | 48,3 | 7,1 | 1,0205 | |||
| GR-156 | 6,84347 | 73,2982 | 98/80 | 39,3 | 0,5 | 1,0389 | |||
| S1 | Grupo Girón | 7,10777 | 72,97111 | Jurásico Tardío- Cretácico Temprano | Jiménez et al., 2022 | 350/10 | 325,7 | 14,8 | 1,014 |
| S2 | 7,10777 | 72,97501 | 270/24 | 324,3 | 5,1 | 1,024 | |||
| S3 | 7,10833 | 72,97805 | 285/18 | 335,8 | 2,5 | 1,013 | |||
| G5 | 7,15683 | 73,1283 | 67/38 | 40,5 | 1,5 | 1,025 | |||
| Zg1 | 6,8982 | 73,1816 | 358/41 | 43 | 15,2 | 1,024 | |||
| Zg2 | 6,89972 | 73,18861 | 344/51 | 30,2 | 8 | 1,02 | |||
| Zg3 | 6,89666 | 73,19138 | 346/28 | 12,8 | -10,7 | 1,032 | |||
| Zg4 | 6,89457 | 73,21051 | 326/36 | 185,6 | -0,5 | 1,039 | |||
| Zls | 6,88805 | 73,22055 | 320/14 | 4,7 | 15,4 | 1,054 | |||
| JD | Jordán | 7,29981 | 73,02225 | Jurásico Temprano | Jiménez et al., 2022 | 136/47 | 48,4 | 1 | 1,02 |
| MJ2 | 7,27621 | 73,0621 | 98/50 | 156,1 | 6,2 | 1,01 | |||
| SJ12 | 6,87437 | 73,11499 | 192/16 | 243,6 | 4,2 | 1,014 | |||
| SJ13 | 6,86509 | 73,10362 | 181/13 | 252,4 | -11,7 | 1,022 | |||
| SJ15* | 6,8596 | 73,09827 | 256/9 | 251,2 | -1,8 | 1,043 | |||
| AJ17 | 6,71388 | 73,06406 | 343/12 | 251 | 11,7 | 1,024 | |||
| PJ7 | 6,98471 | 73,0547 | 317/37 | 16,3 | -13,4 | 1,016 | |||
| B1 | 7,18657 | 73,151 | 111/26 | 3,2 | 0,8 | 1,012 | |||
| B3 | 7,1933 | 73,1539 | 166/12 | 16,7 | 14,1 | 1,019 | |||
| N2 | Noreán | 8,25255 | 73,45274 | Jurásico Temprano | Jiménez et al., 2022 | 258/58 | 180 | 5,1 | 1,013 |
| N3 | 8,25139 | 73,46741 | 113/85 | 15,4 | 14 | 1,021 | |||
| N4 | 8,21847 | 73,4691 | 262/85 | 353,5 | -5,5 | 1,026 | |||
| AR18 | La Rusia | 5,97306 | 73,21021 | Jurásico Medio-Tardío | Jiménez et al., 2022 | 280/71 | 353,5 | 10,7 | 1,016 |
| AR22 | 5,90295 | 73,07212 | 280/36 | 31,6 | 0,1 | 1,017 | |||
| AR25 | 5,90586 | 73,2497 | 311/38 | 207,5 | 3 | 1,036 | |||
| AM21 | Montebel | 5,93843 | 73,11099 | Triásico- Jurásico Temprano | Jiménez et al., 2022 | 323/38 | 184,1 | -12,2 | 1,034 |
| AP27 | Palermo | 5,90149 | 73,21735 | Triásico-Jurásico Temprano | Jiménez et al., 2022 | 295/23 | 48 | 0,5 | 1,054 |
Modelo curve fit para el Triásico-Jurásico Inferior: los 14 sitios de las unidades del Triásico-Jurásico Inferior corresponden a las unidades Montebel en el Anticlinorio de Arcabuco (1 sitio), la Formación Noreán en el flanco oeste del Macizo de Santander (1 sitio) y la Formación Jordán en los bloques colgante y yacente de la Falla de Bucaramanga (Figura 5, Tabla 2). Con base en este conjunto de datos, el modelo curve fit deriva un factor de aplanamiento de 0,79 ± 0,56.
Modelo curve fit para el Jurásico Medio-Cretácico Inferior: los 43 sitios de las unidades del Jurásico Medio-Cretácico Inferior corresponden a las unidades La Rusia en el Anticlinorio de Arcabuco (3 sitios) y el Grupo Girón en el Macizo de Santander (3 sitios), bloque yacente de la Falla de Bucaramanga (1 sitio) y en el Anticlinorio de los Yariguíes (37 sitios) (Figura 6, Tabla 2). Con base en este conjunto de datos el modelo curve fit deriva un valor de aplanamiento de 1,14 ± 0,78.
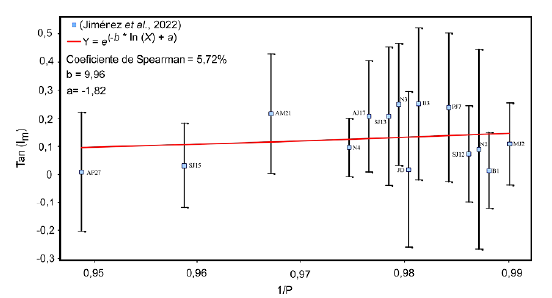
Figura 5 Ajuste y correlación usando curve fit para el conjunto de datos reportados por Jiménez et al. (2022) según la ecuación y filtrando según los criterios descritos. El valor de f para este set de datos es de 0,79 (Ic = 9,20°).

Figura 6 Ajuste y correlación usando curve fit para el conjunto de datos reportados por Jiménez et al. (2021, 2022) según la ecuación y filtrando según los criterios descritos. El valor de f para este set de datos es de 1,14 (Ic = 7,05°).
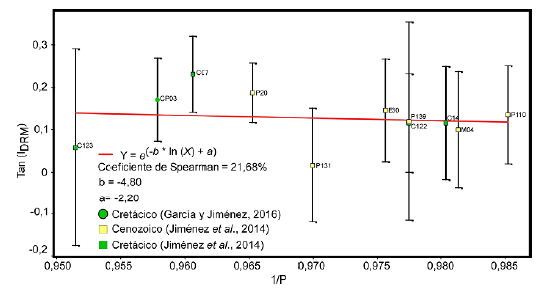
Figura 7 Ajuste y correlación usando curve fit para el conjunto de datos reportados por Jiménez et al. (2014) y García y Jiménez (2016) según la ecuación y filtrando según los criterios descritos. El valor de f para este set de datos es de 1,15 (Ic = 6,27°).
Modelo curve fit para el Cretácico-Cenozoico: los 11 sitios de las unidades del Cretácico al Cenozoico están distribuidos en las unidades Rosablanca, San Gil y Chipaque (4 sitios), Guaduas (4 sitios), Lodolitas de Fusagasugá (1 sitio) y Tilatá (1 sitio), en la zona axial de la Cordillera Oriental y en la Formación Cuervos (1 sitio) en el Catatumbo (Figura 7, Tabla 2). Con base en este conjunto de datos el modelo curve fit deriva un valor de aplanamiento de 1,15 ± 0,21.
Modelo curve fit para la Cordillera Oriental: con base en los 68 sitios de las unidades del Triásico al Cenozoico, distribuidas en la Cordillera Oriental, Macizo de Santander y Catatumbo (Figura 8, Tabla 2), el modelo curve fit deriva un valor de aplanamiento de 1,04 ± 0,6.
Discusión
Las inclinaciones y paleolatitudes reportadas para la Cordillera Oriental (Jiménez et al., 2014, 2015, 2021, 2022; García y Jiménez, 2016) muestran variaciones y dispersiones en las medidas que pueden estar relacionadas con la litología, granulometría, densidad de datos, variaciones de posición latitudinal, normales y reversos, etc. Esto puede causar que en el modelo haya valores fuera de la estadística del dominio del factor de aplanamiento (teóricamente entre 0 y 1). Para casos como este, de alta variabilidad en los datos (factores obtenidos de 1,14, 1,15 y 1,04), el factor debe acotarse al valor máximo posible que es 1, por lo que se debe realizar un filtrado más acorde con la información disponible.
Datos calculados vs datos modelados
Los coeficientes de correlación como el de Pearson o Spearman son medidas que permiten evaluar el grado de relación lineal o monotónica entre variables. Pearson mide relaciones lineales, o cambios proporcionales de una variable con respecto a otra. Por otro lado, Spearman mide el grado en que los cambios de una variable se asocian con los cambios en la misma dirección en otra variable, sin que sean necesariamente proporcionales. A partir de esto es posible definir si el modelo entiende la tendencia o el patrón de los datos.
El coeficiente de Spearman, al ser útil para evaluar relaciones que no son necesariamente lineales, fue calculado para evaluar los modelos obtenidos con curve fit, que utiliza la ecuación 6. Los coeficientes obtenidos para cada uno de los conjuntos de datos presentan valores muy bajos en comparación con el obtenido para los datos de Garcés et al. (1996a): 5,72%, 1,35%, 21,68%, 0,21% y 97,80% para el Triásico-Jurásico Inferior, Jurásico Medio-Cretácico Inferior, Cretácico-Cenozoico, Cordillera Oriental y Garcés et al. (1996a), respectivamente. Esto indica que no se está reflejando una relación entre las inclinaciones calculadas y las modeladas.
Todos los valores de inclinación utilizados por Garcés et al. (1996a) en su ajuste y después de los filtros son mayores a 10°; 56° es el valor mayor. A partir de esto se cambió el filtro: inclinación < |20°| por |25°| > inclinación > = |10°|, y se obtuvieron nuevamente los valores de f junto a un nuevo coeficiente de Spearman. Los resultados se encuentran en la Tabla 3.
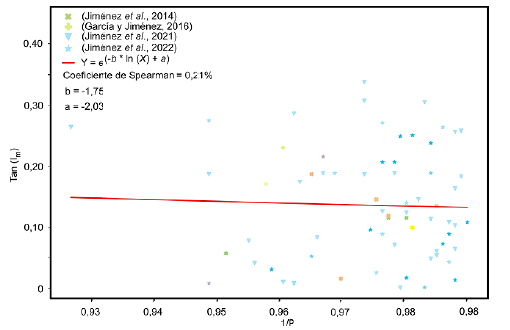
Figura 8 Ajuste y correlación usando curve fit para el conjunto total de datos reportados en la Cordillera Oriental y Macizo de Santander y Catatumbo reportados por Jiménez et al. (2014, 2021, 2022) y García y Jiménez (2016) según la ecuación y filtrando según los criterios descritos (Ic = 7,44°).
Tabla 3 Comparación entre el aplanamiento y el coeficiente de Spearman obtenidos para los datos con los filtros originales vs. el nuevo filtro que no tiene en cuenta ni inclinaciones someras ni muy altas.
| Triásico-Jurásico Inferior | Jurásico Medio- Superior | Cretácico-Cenozoico | Cordillera Oriental | |
|---|---|---|---|---|
| Aplanamiento utilizando filtro inicial | 0,79 ± 0,56 | 1,14 ± 0,78 | 1,15 ± 0,21 | 1,04 ± 0,6 |
| Coeficiente de Spearman (%) | 5,72 | 1,35 | 21,68 | 0,21 |
| Aplanamiento utilizando filtro final | 0,82 ± 0,06 | 0,98 ± 0,20 | 0,46 ± 0,18 | 0,93 ± 0,22 |
| Coeficiente de Spearman (%) | 63,77 | 15,67 | 50 | 8,36 |
Los resultados muestran una mejoría general en los coeficientes de Spearman y en los errores calculados para los valores de aplanamiento, principalmente en las muestras del Triásico-Jurásico Inferior. En el caso de las muestras del Cretácico-Cenozoico, el filtro dejó solo 3 muestras para el cálculo, por lo que no se podría tener en cuenta. Esto permite concluir que el modelo adquiere mayor validez cuando no se tienen datos de inclinaciones someras.
Corrección de la inclinación y paleolatitudes
Jiménez et al. (2021), basados en el método I-E (Tauxe et al., 2008) determinan valores de f para la Formación Angostura del Río Lebrija de 0,6 y para la Formación Los Santos de 0,26, mostraron una gran discrepancia entre la inclinación observada (14°) y la corregida (43,1°), y sugirieron una sobreestimación de la inclinación. El valor de f es inusualmente bajo y podría ser explicado por el bajo número de datos disponible (<100) para el cálculo siguiendo el método de I-E (Tauxe et al., 2008; Jiménez et al., 2021, 2022). Para evitar posibles sobreestimaciones de la inclinación, Jiménez et al. (2021) evalúan 3 valores de f (0,5, 0,6 y 0,7) como factor de corrección, teniendo en cuenta que estos valores son considerados como realistas para el tipo de rocas estudiadas (Bilardello y Kodama, 2010). Finalmente, la inclinación de las rocas del Triásico al Cretácico Inferior fue corregida usando un factor de corrección f de 0,6 (Jiménez et al., 2021, 2022).
Los valores de f determinados usando el modelo curve fit varían entre 0,79 a 1,15, pero utilizando el filtro ajustado a los datos disponibles se tienen valores entre 0,82 y 0,98 (descartando el valor de 0,46 obtenido para Cretácico-Cenozoico por la falta de datos después del filtro para un cálculo significativo). El valor medio obtenido muestra un valor de 0,93, lo cual sugiere que estas rocas no han sido afectadas por aplanamiento y por tanto los valores de las paleolatitudes no varían significativamente. El valor de f 0,93 difiere de la corrección sugerida por Jiménez et al. (2021, 2022) y es coherente con los datos de paleolatitudes reportadas en la Formación Jordán en el área de Bucaramanga (Bayona et al., 2006) y en rocas volcánicas del área de Santa Marta (Bayona et al., 2010), los cuales sugieren traslaciones de bloques desde el hemisferio sur. Un factor de f de 0,93 implica que durante el Triásico al Jurásico Temprano bloques para-autóctonos estarían localizados en el hemisferio sur y fueron transportados desde posiciones entre 14°S y 10°S hacia el norte por la subducción oblicua de la Placa Farallón (Bayona et al., 2006, 2010, 2020; Jiménez et al., 2021, 2022). Durante el Jurásico Tardío a Cretácico Temprano, estos bloques tectónicos se localizaban en el hemisferio norte, cercanos a su posición actual ~7°N (Bayona et al., 2006, 2010, 2020; Jiménez et al., 2021, 2022).
Conclusiones
Con base en el método de Garcés et al. (1996a), para un conjunto de datos reportados de anisotropía de susceptibilidad magnética y datos de paleomagnetismo distribuidos en la Cordillera Oriental, Macizo de Santander y Catatumbo, sumado a un nuevo conjunto de datos de anisotropía de la susceptibilidad magnética en el Anticlinorio de Los Yariguíes, fue posible determinar un valor medio del factor de aplanamiento f) de 1,04 ± 0,6 (0,93 ± 0,22 tras el filtro de inclinaciones someras y muy altas). Este valor sugiere que las inclinaciones observadas no han sufrido procesos de aplanamiento, por lo tanto, las paleolatitudes derivadas sugieren que bloques tectónicos del Triásico a Jurásico Temprano experimentaron traslaciones desde el hemisferio sur. Los bloques tectónicos desde el Jurásico Medio a Cretácico Temprano estarían localizados en latitudes norte cercanos a su posición actual como se sugiere en estudios previos (Bayona et al., 2006, 2010, 2020; Jiménez et al., 2021, 2022).
El error calculado de 0,6 es originado por la mezcla de dos conjuntos de datos. El primer conjunto corresponde a inclinaciones someras y latitudes cercanas a su posición actual; el segundo conjunto de datos corresponde a inclinaciones mayores y latitudes en el hemisferio sur. Al excluir las inclinaciones más altas y bajas del modelo, el error disminuye considerablemente de 0,6 a 0,22 e introduce el valor del factor de aplanamiento dentro de su dominio teórico. El método de corrección utilizado es más efectivo en conjuntos de datos con inclinaciones medias a altas. En particular, se puede afirmar que en la Cordillera Oriental el método de corrección es más aplicable en rocas del Jurásico Temprano.
El número de datos disponibles en la Cordillera Oriental permitió realizar el modelo curve fit según el método de Garcés et al. (1996a); sin embargo, se sugiere que 1) futuros trabajos de paleomagnetismo incluyan datos de anisotropía de susceptibilidad magnética, y que 2) exploren metodologías como la anisotropía de remanencia para estimar el aplanamiento de la inclinación magnética.