Services on Demand
Journal
Article
Indicators
Related links
Share
Revista Colombiana de Química
Print version ISSN 0120-2804On-line version ISSN 2357-3791
Rev.Colomb.Quim. vol.38 no.1 Bogotá Jan./Apr. 2009
ELECTRON ANGULAR DISTRIBUTIONS IN DISSOCIATIVE PHOTOIONIZATION OF THE HYDROGEN MOLECULE
DISTRIBUCIONES ANGULARES ELECTRÓNICAS EN LA FOTOIONIZACIÓN DISOCIATIVA DE LA MOLÉCULA DE HIDRÓGENO
DISTRIBUIÇÕES ANGULARES DE ELÉTRONS NA FOTOIONIZAÇAO DISSOCIATIVA DA MOLÉCULA DE HIDROGÊNIO
Jhon F. Pérez-Torres1,2, José L. Sanz-Vicario3, Fernando Martín2
1 Instituto de Química, Universidad de Antioquia, Medellín, Colombia.
2 Departamento de Química, Universidad Autónoma, Madrid, España.
3 Instituto de Física, Universidad de Antioquia, Medellín, Colombia. sanjose@fisica.udea.edu.co
Recibido: 07/11/08 - Aceptado: 03/04/09ABSTRACT
A method to calculate angular distributions for electrons ejected from fixed-in-space molecular hydrogen molecules subject to ultrashort intense laser pulses is proposed, based on the ab initio solution of the time-dependent Schrodinger equation. This method of solution allows for a temporal picture of interferences arising in the dissociative ionization channel (in the proton kinetic energy spectrum) due to the presence of the autoionizing double excited states in the Hydrogen molecule. In particular, we show how this autoionization during the dissociative photoionization process may also induce a counterintuitive asymmetry in the angular distribution of the ionized electron with respect to nuclei inversion, in spite of dealing with an homonuclear system.
Key words: Ab initio calculations, hydrogen molecule, molecular photoionization, electron angular distributions.
RESUMEN
Se propone un método para calcular distribuciones angulares de electrones ionizados en la molécula de hidrógeno fija en el espacio sometida a pulsos láser intensos y ultracortos, basado en la solución desde primeros principios de la ecuación de Schrodinger dependiente del tiempo. Esta solución nos permite tener una visión temporal de la interferencias generadas en el canal de ionización disociativa (en el espectro de energía cinética de los protones) debido a la presencia de la autoionización de estados doblemente excitados de la molécula de hidrógeno. Se muestra específicamente cómo la autoionización durante el proceso de fotoionización disociativa también puede inducir una asimetría en la distribución angular del electrón ionizado con respecto a la inversión nuclear, un efecto no intuitivo a pesar de estar tratando con un sistema homonuclear.
Palabras clave: cálculos ab initio, molécula de hidrógeno, fotoionización molecular, distribuciones angulares electrónicas.
RESUMO
Propõe-se um método para calcular as distribuições angulares de elétrons ionizados de uma molécula de hidrogênio fixa no espaço, sujeita a pulsos de laser intensos e ultra-curtos, baseado na soluçao desde primeiros princípios da equaçao de Schrõdinger dependente do tempo. Esta soluçao nos permite ter uma visão temporal das interferências geradas no canal de ionizaçao dissociativa (no espectro de energia cinética dos prótons) devido á presença da auto-ionização de estados duplamente excitados da molécula de hidrogênio. Mostra-se especificamente como a auto-ionização durante o processo de foto-ionização dissociativa pode também induzir uma assimetria na distribuição angular do elétron ionizado com respeito á inversão nuclear, um efeito não intuitivo apesar de estar se tratando de um sistema homonuclear.
Palavras-chave: cálculos ab initio, molécula de hidrogênio, fotoionização molecular, distribuições angulares eletrônicas.
INTRODUCTION
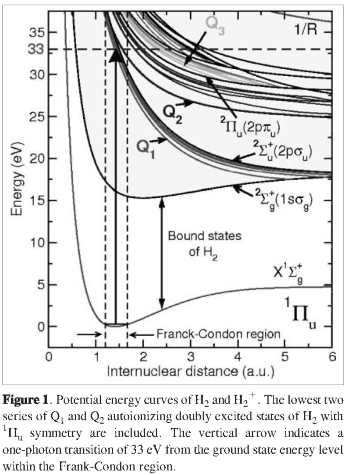
For decades the main concern of quantum chemistry has been the development of methodologies to calculate ab initio binding energies and stable geometrical structures from simple to complex molecules, mostly in their ground state. In dealing with chemical reactivity, quantum chemistry also begins to envisage models and methods for dynamical processes in which not only the ground state but also excited states are involved in the reaction mechanisms. In particular, when molecules are subject to radiation, one opens the way to multichannel reaction phenomena which is the area of study of photochemistry. Nevertheless, even for simple molecules, the processes appearing in laser-molecule interactions may be quite involved indeed and it is quite desirable to have a detailed temporal picture of reactions. In this work we study the ionization photo dynamics of the hydrogen molecule H2 subject to intense ultra short laser pulses with a quantum time-dependent method, specifically when the photon energy takes the molecule to the region where doubly excited states lie above two ionization thresholds. At variance with atoms, the absorbed photon energy is shared between electronic and nuclear degrees of freedom, so that the residual molecular ion H2+ may be left vibrationally excited or in a dissociative state. Keeping the scheme as simple as possible, the reactions of H2 under a laser radiation with photon energies above ~ 23 eV may be summarized as follows:
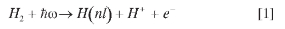

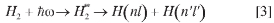
i.e., dissociative ionization [1], non dissociative ionization [2], and the last reaction [3] denotes that dissociation into neutrals which is only mediated by previously populated double excited states H2** These superexcited states are called Q1 resonances (lying above the H2+(1 σg) ionization threshold), Q2 resonances (above the H2+ (2pσu) limit) and so on (see Figure 1). Since these states are immersed into an electronic continuum, they are metastable, a short lifetime in the scale of femtoseconds (fs) is associated to them and after being populated, they autoionize to produce also dissociative ionization [1] or non dissociative ionization [2], which implies a strong interference with the direct absorption reaction. Only those molecules that survive without being autoionized follow the dissociative path to produce excited hydrogen atoms H(nl) [3]. The imprint of the key role that resonant states play in the photo dynamics may be directly appreciated in the distributions of the kinetic energy of protons released after molecular dissociation in reaction [1] and also in the production of atomic excited states H(nl), which eventually decay radiatively. Both events were the subject of recent measurements. Ito et al. (1) measured kinetic energy distributions of the ejected H+ at different photon energies and J.D. Bozek et al. (2) measured the production of Lyman a and Balmer a fluorescence from H(nl) after photodissociation of H2. A sophisticated time dependent theoretical? method to deal with such photo-processes in H2 has already been developed by? our group (3) and it reproduces the experimental data fairly well (2,3,4).
With the recent advent of COLTRIMS spectroscopic techniques (5), kinematically complete experiments, where the momenta of all charged particles is determined at each single event, are becoming available and now they represent a challenge to the theorist. Inparticular, for the dissociative ionization process [1], the experiment is able to determine the orientation of the hydrogen molecule at the time of electron ejection by photon impact. Since the orientation at a given time is known, one may claim that the electron came from a fixed-in-space molecule. Therefore, we develop a procedure to compute such angular distributions for the ionized photoelectrons and, since electronic and nuclear motions are coupled, we show their explicit dependence on the proton kinetic energy release.
METHOD OF SOLUTION
Our method is based on the solution of the time dependent Schrödinger equation (TDSE), which is appropriate when the laser-molecule interaction happens to occur in the time scale ofatto- and femtoseconds (fs) and the laser intensity is large enough to invalidate perturbative approaches. Thus we solve the TDSE for the hydrogen molecule,
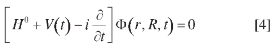
where H0 is the field-free Hamiltonian of H2 in the body-fixed frame and V (t) = p A(t) represents the field interaction potential in the velocity gauge. A cosine-square modulated pulse with photon energy ω and duration T is switched on/off in the interval [0, T]. We then perform a close-coupling expansion of the time-dependent molecular wave function:
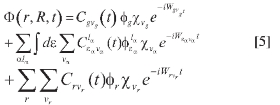
in terms of vibronic (electronic Φ and nuclear Χ states of the ground g, continuum for each channel α with energy εα and angular momentum lα of the ionized electron, and resonant states r of H2. By inserting this expansion into the TDSE, a set of coupled differential equations is obtained and solved numerically from time t = 0 (when the laser pulse starts) up to a time t > T when the pulse is already gone. To compute total energies Wnv and electronic and vibrational wave functions included in [5] we cannot rely on the plethora of standard computational codes available for the theoretical chemist. In particular, the calculation of resonant and continuum states of molecules are still a no man's land in standard chemical computations, so that one has to tailor his own computer codes. The ground state of H2 is evaluated by expanding the electronic wave function Φg in a basis of configurations built from H2+ orbitals, which are represented in a one-center expansion in terms of B-splines basis within a radial box. The continuum wave functions 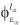 are calculated using a L2 close-coupling method by using the same set of H2+ orbitals but with a well-defined angular momentum l for the escaping electron, which ensures that correct boundary conditions are imposed. The series of Qn resonant states are obtained from the QH0Q Feshbach-projected electronic Hamiltonian, with a configuration interaction method too. Vibrational wave functions were also computed in terms of B-splines basis for each electronic state. For further details the reader is referred to Ref. (3).
are calculated using a L2 close-coupling method by using the same set of H2+ orbitals but with a well-defined angular momentum l for the escaping electron, which ensures that correct boundary conditions are imposed. The series of Qn resonant states are obtained from the QH0Q Feshbach-projected electronic Hamiltonian, with a configuration interaction method too. Vibrational wave functions were also computed in terms of B-splines basis for each electronic state. For further details the reader is referred to Ref. (3).
The ionization cross section, 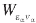 differential in the energy, for one photon absorption is computed from the coefficients
differential in the energy, for one photon absorption is computed from the coefficients 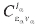 (t) for t >T with the expression:
(t) for t >T with the expression:
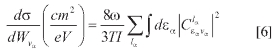
where the photon energy ω is given in Joules, the laser intensity I in W/cm2 and the laser duration T in seconds. In order to compute electron angular distributions in the ionization channel, the final wave function [5] at time t > T must be projected onto the asymptotic incoming wave function (expanded in partial waves) that represents a free electron with energy εα plus a residual ion H2+, left in channel a. After some algebra, one arrives to the following expression for the density of probability differential in both proton kinetic energy EH+ and the solid angle Q for the ejected electron:
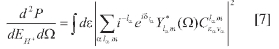
where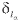 corresponds to the Coulomb phase shift. Short-range phase shifts are already included in the coefficients
corresponds to the Coulomb phase shift. Short-range phase shifts are already included in the coefficients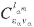 during the propagation. Note also that for dissociative ionization,
during the propagation. Note also that for dissociative ionization, 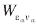 is related to the center-of- mass energy of the ejected protons,
is related to the center-of- mass energy of the ejected protons, 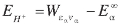 where
where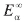 is the asymptotic energy of an H atom separated from an H+ for the channel α.
is the asymptotic energy of an H atom separated from an H+ for the channel α.
RESULTS
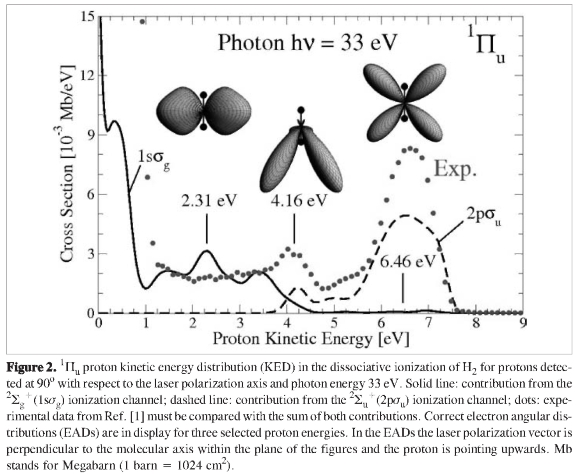
To illustrate the performance of our method we provide results for the dissociative ionization of H2 subject to a laser pulse with a photon energy of ω = 33 eV, intensity I = 1012 W/cm2 and pulse duration T = 10 fs, perpendicularly polarized to the internuclear axis. Dipole selection rules imply that only the 1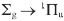 transition takes place. At this photon energy the ground state is excited to the Q2 series of resonances (see Figure 1) along with the underlying two nonresonant continua corresponding to the open channels H2+(1s&sigmag)+e(εl) and H2+(2pσu)+e(εl). Figure 2 shows the kinetic energy distributions (KED) for the final continuum calculated following (6) at photon energy ω = 33 eV and pulse duration T = 10 fs, with separate contributions from H2+(1sσg) and H2+(2pσu) thresholds and it is compared with the experimental results by Ito et ál. (1), for protons observed at 90o with respect to the field polarization axis. The peaks structure in the KED for 1sσg and 2pσu curves only appears due to the presence of the autoionization of the Q1 and Q2 resonances, that produces H2+(1sσg)+e(εl) (both Q1 and Q2) and H2+(2pσu) + e(εl) (only Q2). Closing the autoionization pathway, one should obtain simple Frank-Condon absorption profiles without peaks structure.
transition takes place. At this photon energy the ground state is excited to the Q2 series of resonances (see Figure 1) along with the underlying two nonresonant continua corresponding to the open channels H2+(1s&sigmag)+e(εl) and H2+(2pσu)+e(εl). Figure 2 shows the kinetic energy distributions (KED) for the final continuum calculated following (6) at photon energy ω = 33 eV and pulse duration T = 10 fs, with separate contributions from H2+(1sσg) and H2+(2pσu) thresholds and it is compared with the experimental results by Ito et ál. (1), for protons observed at 90o with respect to the field polarization axis. The peaks structure in the KED for 1sσg and 2pσu curves only appears due to the presence of the autoionization of the Q1 and Q2 resonances, that produces H2+(1sσg)+e(εl) (both Q1 and Q2) and H2+(2pσu) + e(εl) (only Q2). Closing the autoionization pathway, one should obtain simple Frank-Condon absorption profiles without peaks structure.
The origin of asymmetric electron angular distributions is attributed to the Q2 autoionization decay into the two open channels mentioned above and the due interference between these two pathways. To satisfy the final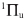 symmetry, the angular momentum for the emitted electron must be l = 1,3,5,... (p-,f-,.. ungerade waves) for the H2+(2sg) gerade threshold, and l=2,4,... (d-,g-,.. gerade waves) for the H2+(2pσu) ungerade threshold. Electron angular distributions included in Figure 3 are taken at proton kinetic energies 2.31 eV, 4.16 eV and 6.46 eV and when the residual ion is left either in the H2+(1sσg) state or in the H2+(2pσu) state. At 2.31 eV, for instance, the 1sag case clearly shows a dominant contribution of the p-wave and the 2pσu,ofa d-wave. One observes that these distributions are fully symmetrical with respect to nuclei inversion. However, molecular states as built in the LCAO model of the chemical bond dissociate into a mixture of atomic orbitals, i.e.,
symmetry, the angular momentum for the emitted electron must be l = 1,3,5,... (p-,f-,.. ungerade waves) for the H2+(2sg) gerade threshold, and l=2,4,... (d-,g-,.. gerade waves) for the H2+(2pσu) ungerade threshold. Electron angular distributions included in Figure 3 are taken at proton kinetic energies 2.31 eV, 4.16 eV and 6.46 eV and when the residual ion is left either in the H2+(1sσg) state or in the H2+(2pσu) state. At 2.31 eV, for instance, the 1sag case clearly shows a dominant contribution of the p-wave and the 2pσu,ofa d-wave. One observes that these distributions are fully symmetrical with respect to nuclei inversion. However, molecular states as built in the LCAO model of the chemical bond dissociate into a mixture of atomic orbitals, i.e.,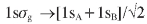 and
and 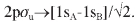 These delocalized molecular orbitals are not truly connected with what one expects from a COLTRIMS experiment. Asymptotically, any experimental device will measure a localized electron bound in an H atom in a well-defined atomic state H(nl) plus a proton, a picture not provided by gerade or ungerade states. Accordingly, we must then project the total wave function onto the correct 1sA ~1sσg + 2pσu linear combination that breaks the gerade-ungerade symmetry. Ultimately this amounts to amend expression [7] by undoing the g-u mixing. Consequently, electrons coming from the two g-u channels interfere, even and odd electron angular momenta I contribute now simultaneously and as a result, the angular distributions become asymmetric with respect to nuclei inversion, mainly when the contributions from the two thresholds overlap at ~ 4 eV and none of them is dominant (see Figure 2 for the correct angular distributions). This fundamental result on symmetry breaking has already been predicted by a time-independent method and confirmed experimentally (6). Nonetheless, the main advantage of the present time-dependent method is the possibility to understand in the time domain the formation and evolution of KED spectra and electron angular distributions. For instance, Figure 4 includes four snapshots at different propagation times during the pulse duration, in which one may appreciate the onset of the autoionization process in the formation of peaks interference structures in KED and also in the symmetry breaking in the electron angular distributions. Furthermore, this asymmetry seems to be independent to the direction in which the proton is emitted (compare the oscillating nature from t = 5.0 fs and t = 7.4 fs angular distributions at EH+ =4.16 eV) precluding any explanation of this effect in terms of a post-collisional electron-proton electrostatic interaction.
These delocalized molecular orbitals are not truly connected with what one expects from a COLTRIMS experiment. Asymptotically, any experimental device will measure a localized electron bound in an H atom in a well-defined atomic state H(nl) plus a proton, a picture not provided by gerade or ungerade states. Accordingly, we must then project the total wave function onto the correct 1sA ~1sσg + 2pσu linear combination that breaks the gerade-ungerade symmetry. Ultimately this amounts to amend expression [7] by undoing the g-u mixing. Consequently, electrons coming from the two g-u channels interfere, even and odd electron angular momenta I contribute now simultaneously and as a result, the angular distributions become asymmetric with respect to nuclei inversion, mainly when the contributions from the two thresholds overlap at ~ 4 eV and none of them is dominant (see Figure 2 for the correct angular distributions). This fundamental result on symmetry breaking has already been predicted by a time-independent method and confirmed experimentally (6). Nonetheless, the main advantage of the present time-dependent method is the possibility to understand in the time domain the formation and evolution of KED spectra and electron angular distributions. For instance, Figure 4 includes four snapshots at different propagation times during the pulse duration, in which one may appreciate the onset of the autoionization process in the formation of peaks interference structures in KED and also in the symmetry breaking in the electron angular distributions. Furthermore, this asymmetry seems to be independent to the direction in which the proton is emitted (compare the oscillating nature from t = 5.0 fs and t = 7.4 fs angular distributions at EH+ =4.16 eV) precluding any explanation of this effect in terms of a post-collisional electron-proton electrostatic interaction.
CONCLUSION
We present a time dependent method to compute proton kinetic energy distributions and electron angular distributions coming from photodissociative ionization of H2, just the theoretical ingredients to fully compare with kinematically complete experiments (COLTRIMS). Asymmetric photoe-lectron angular distributions may arise in H2 (in general, in any symmetric molecule) due to the interference between the gerade and ungerade electron waves, when the excited molecule decays through autoionization onto two dissociative ionization channels pertaining to different gerade or ungerade symmetries of the residual molecular ion H2+.
ACKNOWLEDGEMENTS
J.F.P-T acknowledges a PhD grant E07D401391CO from the Programme Alban, the European Union Programme of High Level Scholarships for Latin America, J.L.S-V thanks financial support from Vicerrectoría de Investigación (CODI) at Universidad de Antioquia and Colciencias agency and F. Martín from DGI project FIS2006-00298 (Spain).
REFERENCES
1. Ito, K.; Hall, R. I.; Ukai, M. Dissociative photoionization of H2 and D2 in the energy region of 25-45 eV.J. Chem.Phys. 1996.104: 8449-8457. [ Links ]
2. Bozek, J. D.; Furst, J. E.; Gay, T. J.; Gould, H.; Kilcoyne, A. L. D.; Machacek, J. R.; Martin, F.; McLaughlin, K. W.; Sanz-Vicario, J. L. Production of excited atomic hydrogen and deuterium from H2 and D2 photodissociation. J. Phys. B: At. Mol. Opt. Phys. 2006. 39: 4871-4882. [ Links ]
3. Sanz-Vicario, J. L.; Bachau, H.; Martin, F. Time-dependent theoretical description of molecular autoio-nization produced by femtosecond xuv laser pulses. Phys. Rev. A. 2006. 73: 033410-1,033410-12. [ Links ]
4. Sanz-Vicario, J. L.; Palacios, A.; Cardona, J. C.; Bachau, H.; Martin, F. Ab initio time dependent method to study the hydrogen molecule exposed to intense ultrashort laser pulses. J. Electron Spectrosc. Relat. Phenom. 2007. 161: 182-187. [ Links ]
5. Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L. P. H.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 2003, 66: 1463-1545. [ Links ]
6. Martin, F. et ál. Single photon-induced symmetry breaking of H2 dissociation. Science, 2007 . 315: 629-633. [ Links ]