Introducción
Los antibióticos son compuestos químicos que tienen la capacidad de tratar enfermedades producidas por bacterias. Históricamente, estos compuestos han sido sintetizados en gran magnitud desde el descubrimiento de la penicilina y su uso ha sido muy amplio en las últimas décadas [1]. El uso indiscriminado de estos fármacos en medicina humana y animal ha ocasionado un impacto negativo en el medio ambiente debido a la falta de métodos eficientes para el tratamiento de efluentes líquidos. Esto ha producido una gran preocupación por la resistencia antimicrobiana que puede producir la gran cantidad de desechos presentes en el medio ambiente [2]. De igual manera, según el informe O'Nell del 2014, el gobierno británico ha considerado que las infecciones resistentes a los antimicrobianos podrían convertirse en la principal causa de muerte en el mundo para el año 2050 [3]. Actualmente, uno de los antibióticos beta-lactámicos más utilizados a escala mundial para el tratamiento de enfermedades infecciosas producidas por bacterias es la amoxicilina, la cual representa uno de los antibióticos más prescritos en Europa y Estados Unidos [4]. En las últimas décadas, el uso de este compuesto ha generado altos niveles de concentración en el medio ambiente, especialmente en fuentes de aguas superficiales, aguas subterráneas potables y residuales [5], [6]. En este caso, los métodos experimentales para la degradación de este compuesto no han sido efectivos debido a la estructura molecular compleja que presenta con diferentes grupos funcionales similares a los aminoácidos presentes en las proteínas [7], [8]. Particularmente, debido a su estructura molecular, la amoxicilina presenta diferentes formas iónicas como función del pH cuando se encuentra disuelta en agua (ver Figura 1). También, estas características estructurales favorecen la solubilidad de la amoxicilina en agua (entre 25 y 300 mg/mL a 25°C); esta especie es muy soluble en agua pura a pH~7 [9]. Esta propiedad fisicoquímica le permite una alta permanencia en fase acuosa por un largo tiempo, lo que favorece que este compuesto pueda ser absorbido y bioacumulado por plantas y animales [10], [11].
Diferentes técnicas experimentales han sido empleadas con la finalidad de reducir la concentración de amoxicilina en agua [12], [13]. Por ejemplo, las técnicas de encapsulamiento y precipitación con surfactantes y polímeros permiten la reducción de la concentración de este tipo de compuestos farmacéuticos betalactámicos en agua [14]. Así mismo, el proceso foto-Fenton ha sido empleado para la degradación de la amoxicilina en solución acuosa en moléculas más simples [15], [16]. En este proceso, a nivel molecular, la conformación espacial de la amoxicilina y su interacción con el agua tienen un papel fundamental en el camino de la reacción involucrada en la degradación de esta especie en el campo experimental. Así, desde el punto de vista molecular, las técnicas de simulación molecular, como los cálculos mecánico-cuánticos y la dinámica molecular, permiten dilucidar el arreglo espacial, la conformación y las interacciones moleculares de los compuestos químicos en diferentes medios solventes [17]-[20]. Estas técnicas de simulación molecular han permitido evaluar el comportamiento de las moléculas a nivel microscópico, lo cual permite obtener una visión más amplia de los sistemas químicos [21]-[23].
En este sentido, en este trabajo se llevó a cabo un análisis conformacional de la amoxicilina en agua mediante dos procedimientos combinando diferentes técnicas de simulación molecular: a) con solvatación implícita mediante cálculos mecánico-cuánticos y b) con solvatación explícita usando dinámica molecular. Además, se evaluó el alcance de ambos procedimientos para la obtención de la conformación espacial más estable tomando en cuenta el efecto que tiene el solvente sobre la estimación de las conformaciones espaciales [24], [25]. Finalmente, se exploró el comportamiento molecular de la amoxicilina en fase acuosa mediante dinámica molecular, con la finalidad de comprender la importancia de las interacciones moleculares en la estabilidad de esta especie en este medio solvente. Los resultados obtenidos pueden contribuir a una mejor comprensión de la cinética química de degradación de la amoxicilina, en medio acuoso, por procesos químicos y fotoquímicos.

Figura 1 Estructuras iónicas de amoxicilina involucradas en los diferentes equilibrios de disociación.
Metodología empleada
La estructura molecular de la amoxicilina presenta diferentes grupos funcionales similares a los contenidos en los aminoácidos (ver Figura 2), lo cual le permite tener valores de pKa iguales a 3,2 y 11,7 [26], [27] asociados al grupo ácido y la amina primaria presentes en su estructura (ver Figura 1).
Para llevar a cabo el análisis conformacional de la amoxicilina en agua se utilizaron dos estrategias de simulación molecular. En este caso, las estrategias involucran el uso de los métodos de solvatación implícita y explícita. El método mecánico-cuántico conductor polarizable continuo (C-PCM por sus siglas en inglés) [28]-[30] fue utilizado para la solvatación implícita y el método de solvatación explícita fue desarrollado con simulaciones de dinámica molecular con moléculas de agua rodeando a la amoxicilina.
Inicialmente, la molécula de amoxicilina fue construida en la herramienta Draw Structure de la página web PubChem [31]. Esta estructura fue optimizada con el software Avogadro (versión 1.2.0) y almacenada en el formato *.mol [32]. Cabe destacar que la estructura molecular puede ser diseñada directamente en el software Avogadro u otros softwares que sirvan de interfaz gráfica. Además, la construcción de la estructura de la amoxicilina fue realizada de tal manera que no se refleja el puente de hidrógeno intramolecular en el grupo carboxílico, con la intención de evaluar la influencia de la conformación inicial de la estructura molecular en el análisis conformacional. En este primer procedimiento, la estructura molecular optimizada fue usada en el programa Ballon-v1.8.2 [33] para producir las diferentes configuraciones estructurales denominadas conformaciones. Este programa utiliza el modelo de energía potencial MMFF94 [34] para obtener configuraciones optimizadas con diferentes arreglos espaciales a partir de una conformación inicial. Sin embargo, este programa no fue capaz de determinar el puente de hidrógeno intramolecular a partir de la conformación inicial utilizada. Un total de 57 conformaciones espaciales para la amoxicilina fueron obtenidas utilizando los parámetros por defecto asignados al programa (--nconfs 100, --nGenerations 300). Estas conformaciones fueron visualizadas mediante el software wxMacMolPlt [35] donde se procedió a preparar las entradas (inputs) con extensión "*.inp" para realizar la optimización geométrica de estas estructuras usando el software Gamess-US (versión 2021-R2) [36]-[38]. Estas conformaciones espaciales fueron optimizadas en el vacío para evaluar la estabilidad de estos arreglos moleculares en este medio. En este procedimiento, todas las configuraciones espaciales fueron optimizadas en el vacío con el funcional híbrido DFT/M06-2X [39] en el nivel 6-31G+(d,p) [40]. Luego, a todas las conformaciones optimizadas se les realizaron cálculos tipo single point de solvatación implícita utilizando el método de solvatación C-PCM con el mismo funcional DFT/M06-2X [39] a un nivel 6-31G+(d,p) [40] para determinar su energía de solvatación en agua. El método de solvatación determina la energía necesaria para transferir la molécula desde el vacío hacia el medio solvente, en donde se incluye la energía necesaria para construir la cavidad dentro del solvente en la cual va a ser insertada la molécula del soluto. Las contribuciones dispersivas a la energía de solvatación fueron obtenidas con el método de solvatación universal (SMD por sus siglas en inglés) [41]. Como resultado del proceso de simulación se obtienen los archivos de salida output con extensión ".log" de donde se obtiene la información de la energía libre de solvatación para el análisis conformacional. La energía de solvatación, AGsolv, es definida por la Ec. (1):
En donde el término AGelec corresponde a la contribución electrostática a la energía de solvatación y el término AGcds corresponde a la contribución energética asociada a la construcción de la cavidad dentro del solvente y las interacciones dispersivas entre el soluto y el solvente. Una vez realizado el análisis de las energías en todas las conformaciones, se tomaron las cinco estructuras moleculares con las energías libres de solvatación más favorables y estas estructuras fueron optimizadas con el método de solvatación C-PCM [28]-[30] con el mismo funcional DFT/M06-2X [39] a un nivel 6-31G+(d,p) [40]. Además, se tomaron cinco conformaciones estructurales con el puente de hidrógeno intramolecular en el grupo -COOH más estables en agua para realizar una comparación entre las energías de solvatación obtenidas. En la segunda estrategia, usando solvatación explícita, la molécula de amoxicilina fue colocada en el centro de una caja cúbica de dimensiones 5x5x5 nm3. En esta misma caja, la amoxicilina fue solvatada con un total de 4150 moléculas de agua. La configuración inicial de la amoxicilina en agua es mostrada en la Figura 3.

Figura 3 Estructura molecular de la amoxicilina con moléculas de agua en una caja cúbica bajo condiciones de contornos periódicos.
Inicialmente, una simulación de minimización de energía fue realizada para relajar las configuraciones de las moléculas dentro de la caja con el procedimiento steep descent [42]. Seguidamente, al sistema relajado se le realizó una simulación de dinámica molecular tipo NVT a una temperatura de 298,15 K. En este ensamble tipo NVT, el número de partículas, el volumen de la caja de simulación y la temperatura son mantenidos constantes y se observa la variación de la energía total del sistema. La temperatura fue controlada con el método v-rescale [43]. El radio de interacción utilizado para determinar las interacciones de vdw fue de 1,25 nm y el método de Ewald [44] fue empleado para determinar las contribuciones electrostáticas. Las condiciones de contornos periódicas fueron mantenidas en las dimensiones xyz. La longitud de las simulaciones fue de 20 ns y las configuraciones fueron almacenadas cada 1 ps, generando un total de 20.000 conformaciones. En esta parte, los force fields OPLS-AA [45] obtenido en el servidor LigParGen [46] y TIP4P [47], [48] fueron utilizados para describir las moléculas de amoxicilina y agua, respectivamente. La construcción y la simulación del sistema fueron realizadas con el programa Gromacs (versión 2019.2) [49], [50]. El análisis conformacional fue realizado evaluando la raíz cuadrada de la desviación cuadrática media de las posiciones de los átomos, RMSD, en el espacio ocupado definido por la Ec. (2):
En esta ecuación (2), rn i es la posición del átomo n en la conformación i y el término rn ref corresponde a la posición del átomo n en la conformación inicial de referencia.
Resultados y discusión
Exploración de las conformaciones de la amoxicilina usando cálculos mecánico-cuánticos
En esta parte se obtuvieron diferentes conformaciones espaciales para la amoxicilina sin presencia del puente de hidrógeno intramolecular en el grupo -COOH en el vacío utilizando el programa de generación de conformaciones balloon-v-1.8.2 [33]. La estabilidad fue evaluada en función de la energía total de estas conformaciones estructurales y la energía libre de solvatación estimada usando un cálculo tipo single point (ver Figura 4(a)). En la Figura 4(a) se puede apreciar que la conformación identificada como C1 corresponde a la conformación inicial utilizada. La energía total obtenida muestra que esta conformación C1 es la más estable en el vacío en comparación con el resto de conformaciones evaluadas. También, utilizando la conformación C1 como la configuración de referencia más estable en el vacío, se observa que otras conformaciones identificadas como C5, C15 y C20 tienen una considerable estabilidad en el vacío equivalente a la conformación C1. Seguidamente, para comparar de forma eficiente la estabilidad de las conformaciones espaciales se determinó la energía relativa de cada conformación en el vacío utilizando la conformación C1 como la más estable (ver Figura 4(b)). La Figura 4(b) muestra que el resto de las conformaciones son menos estables en comparación con la configuración C1, lo cual indica que todas las conformaciones obtenidas según el procedimiento de balloon-v-1.8.2 [33] tienen una menor estabilidad energética en el vacío según los cálculos mecánico-cuánticos. Para este caso, las conformaciones C5, C15 y C20 tienen valores de energías relativas de 1,38; 0,58 y 3,33 kJ/mol en comparación a la conformación C1. Estas conformaciones estructurales son las más estables en el vacío en conjunto con la conformación C1 usada para generar las conformaciones estructurales en este programa.
Adicionalmente, las energías libres de solvatación de las 57 configuraciones fueron calculadas y sus valores son mostrados en la Figura 4(c), en la cual se observa que la conformación más estable en el medio solvente corresponde a la configuración C56 (AGsolv igual a -98,16 kJ/mol). Para este caso, esta conformación estructural tiene la energía libre de solvatación más favorable, lo cual indica que este arreglo espacial cuenta con una interacción favorable con el agua que ha sido descrita de forma implícita. A su vez, otras conformaciones espaciales identificadas como C43 (AGsolv igual a -95,90 kJ/mol) y C51 (AGsolv igual a -95,73 kJ/mol) tienen energías libres de solvatación más favorables para este medio solvente. También, se puede observar que las conformaciones espaciales C56, C43 y C51 para la amoxicilina son más favorables en el agua que en el vacío. Un hecho notable que muestran los resultados es que la conformación inicial C1 es una de las conformaciones que tienen una energía de solvatación menos favorable con respecto a las estructuras evaluadas, lo cual indica que se debe ser bien selectivo en la estructura de partida para realizar el análisis conformacional. En la Figura 5 se muestran los arreglos espaciales de las conformaciones más estables en el vacío y el medio acuoso.
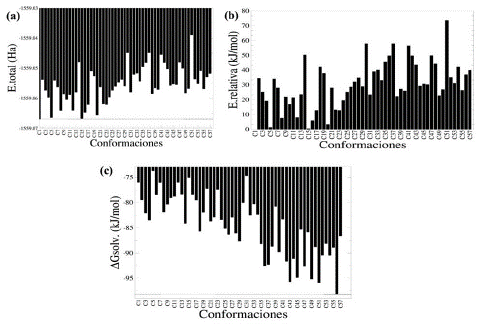
Figura 4 Energías para las conformaciones estructurales construidas sin el puente hidrógeno en el grupo carboxílico. (a) Energías totales de cada conformación. (b) Energías relativas calculadas usando como referencia la molécula más estable (conformación C1). (c) Energía libre de solvatación para cada conformación, calculada con el método de solvatación SMD usando como solvente el agua.
En la Figura 5(a) se observa que la conformación C1 para la molécula de amoxicilina está completamente extendida en el vacío con el grupo -NH2 interaccionando con el grupo -NH localizado cerca del anillo beta-lactámico. En la Figura 5(b), en el vacío, la molécula de amoxicilina muestra una conformación espacial ligeramente extendida. En esta conformación se observa la interacción tipo puente de hidrógeno entre el protón del ácido carboxílico con el grupo carbonilo más cercano. En cambio, en la Figura 5(c) se observa una molécula con un arreglo espacial plegado en donde el anillo aromático interacciona con el grupo carbonilo más cercano y el átomo de hidrógeno del grupo carboxílico con el nitrógeno presente en el anillo beta-lactámico. Para las conformaciones en el medio acuoso, se observa en la Figura 5(d) que la conformación C43 tiene una conformación espacial semiplegada en donde el átomo de hidrógeno del grupo -COOH interacciona con el anillo aromático y el grupo -NH2 de la molécula. En la conformación C51 (ver Figura 5(e)), la amoxicilina se muestra ligeramente contraída con el átomo de hidrógeno del grupo -COOH en interacción con el grupo cetónico localizado en el anillo beta-lactámico. En la Figura 5(f), la amoxicilina con la conformación C56 se encuentra semiplegada con el átomo de hidrógeno del grupo -NH en interacción con el grupo -NH2 formando un puente de hidrógeno intramolecular. En esta conformación, que corresponde a la más estable en agua, los grupos funcionales están expuestos completamente hacia el agua como solvente implícito. Finalmente, estos resultados demuestran que es fundamental hacer la exploración de las conformaciones estructurales en un medio solvente para identificar la conformación más estable de esta molécula. En este caso, el programa balloon-v-1.8.2 [33] permite obtener diferentes conformaciones espaciales en el vacío, pero luego se debe identificar, usando un proceso de solvatación, la conformación más estable, lo cual requiere de mayor poder computacional.
Evaluación de las energías libres de solvatación para las conformaciones más estables de la amoxicilina sin puente de hidrógeno y con puente de hidrógeno
En esta parte, las estructuras con las energías libres de solvatación más favorables fueron utilizadas para evaluar a mayor profundidad el efecto del puente de hidrógeno intramolecular del grupo -COOH en la estabilidad de estas conformaciones en el medio acuoso. Las conformaciones de la amoxicilina C56, C51, C43, C49 y C45 fueron utilizadas como estructuras sin puente de hidrógeno en el grupo -COOH. A su vez, las conformaciones C5, C47, C29, C34 y C56 fueron usadas como estructuras con puente de hidrógeno en el grupo -COOH. Estas estructuras fueron seleccionadas por mostrar los grupos funcionales polares expuestos al medio solvente. Cada una de estas conformaciones fue optimizada en el medio solvente usando el método de solvatación C-PCM junto con el método SMD. Las contribuciones a la energía libre de solvatación fueron determinadas y sus valores son reportados en las Tablas 1 y 2 para las conformaciones estudiadas. En la Tabla 1 los valores de energía libre de solvatación muestran que la conformación C56 es más favorable en fase acuosa. En este caso, la conformación espacial C56 pasó de una configuración semiplegada a un arreglo plegado en el proceso de optimización geométrica. También, esta conformación tiene la contribución electrostática más alta a la energía de solvatación, lo cual sugiere que los grupos polares de la molécula de amoxicilina están más expuestos a la interacción con el agua en esta conformación. Para la contribución electrostática se muestra el siguiente orden decreciente de contribución a la energía de solvatación: C56 > C49 > C51 > C43 > C45. A su vez, se observa que la conformación C49 tiene la contribución cavidad-dispersiva-repulsiva más alta en comparación con el resto de las estructuras conformacionales evaluadas. En este caso, la conformación C49 requiere de una mayor energía para construir la cavidad del solvente y genera la mayor repulsión con el agua. En este caso, la energía libre AGcds tiene el siguiente orden decreciente: C49 > C56 > C45 > C43 > C51, el cual es muy distinto al mostrado en la contribución electrostática. Aquí se puede apreciar que las energías libres de solvatación son dependientes del arreglo molecular de la especie evaluada en el medio solvente y de la exposición de los grupos polares en el momento de hacer la optimización geométrica.
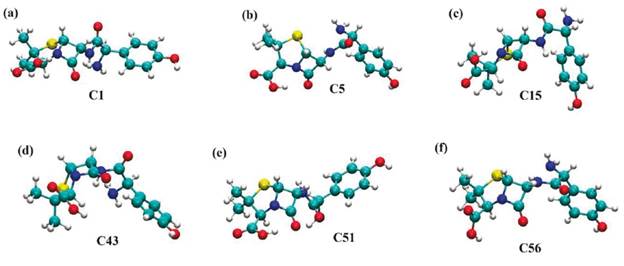
Figura 5 Conformaciones estructurales de la amoxicilina más estables obtenidas de los cálculos mecánico-cuánticos en el vacío y el agua descrita como solvente implícito. (a), (b) y (c) corresponden a las conformaciones C1, C5 y C15 más estables en el vacío. (d), (e) y (f) corresponden a las conformaciones C43, C51 y C56 más estables en el agua.
En la Tabla 2 se muestra que las contribuciones a la energía libre de solvatación para las conformaciones formando el puente de hidrógeno intramolecular en el grupo -COOH son de mayor magnitud en comparación a las reportadas sin puente de hidrógeno en la Tabla 1. La ganancia de estabilidad con respecto a la energía libre de solvatación es considerable en comparación con las conformaciones sin el puente de hidrógeno intramolecular en la amoxicilina. Para este caso, las conformaciones con el puente de hidrógeno intramolecular presentan energías libres de solvatación entre -110 y -130 kJ/mol. La conformación C34 tiene la energía libre de solvatación más favorable en comparación con el resto de conformaciones. Además, se observa que la contribución cavidad-dispersiva-repulsiva (AGcds) asociada a la energía libre de solvatación varía ligeramente en comparación con la contribución electrostática (AGelec). En este caso, se observa que la contribución electrostática sigue este orden decreciente de afinidad con el agua: C34 > C29 > C56 > C5 > C47. En cambio, la contribución AGcds, que indica la cantidad de energía necesaria para construir la cavidad en el solvente, muestra la siguiente tendencia en las conformaciones estudiadas: C5 > C56 > C34 > C29 > C47.
Tabla 1 Energías libres de solvatación (AGsolv) de las conformaciones más estables en agua de la amoxicilina sin puente hidrógeno intramolecular en el grupo -COOH. Se muestra la contribución electrostática (AGelec) a la energía libre de solvatación, la contribución asociada a la energía libre necesaria para construir la cavidad y la interacción dispersiva-repulsiva en el medio solvente (AGcds).
| Conformación | AGelec | AGcds | AGsolv |
|---|---|---|---|
| espacial | (kJ/mol) | (kJ/mol) | (kJ/mol) |
| C56 | -158,87 | 32,26 | -98,16 |
| C51 | -152,97 | 28,33 | -95,89 |
| C43 | -151,46 | 29,46 | -95,73 |
| C49 | -155,02 | 34,02 | -95,19 |
| C45 | -150,04 | 30,54 | -94,89 |
Tabla 2 Energías libres de solvatación (AGsolv) de las conformaciones de la amoxicilina con puente hidrógeno intramolecular en el grupo -COOH. Se muestra la contribución electrostática (AGelec) a la energía libre de solvatación, la contribución asociada a la energía libre necesaria para construir la cavidad y la interacción dispersiva-repulsiva en el medio solvente (AGcds).
| Conformación espacial | AGelec (kJ/mol) | AGcds (kJ/mol) | AGsolv (kJ/mol) |
|---|---|---|---|
| C5 | -148,28 | 34,98 | -113,30 |
| C47 | -142,76 | 31,21 | -111,55 |
| C29 | -152,55 | 32,76 | -119,79 |
| C34 | -154,89 | 33,47 | -121,42 |
| C56 | -151,54 | 34,39 | -117,15 |
Estos resultados muestran que el arreglo intramolecular tiene una gran influencia en la estabilidad que presenta la molécula en el medio solvente en estudio. En este caso, se observa que las conformaciones espaciales con el puente de hidrógeno intramolecular en el grupo -COOH tienen la más alta estabilidad en agua. En la Figura 6 se muestran las conformaciones espaciales que fueron evaluadas en esta parte. En este caso, la Figura 6(e) corresponde a la conformación C56 que es la más estable en agua sin puente de hidrógeno en el grupo -COOH. En esta conformación la amoxicilina tiene un arreglo espacial semi extendido. Sin embargo, se presentan diferentes interacciones intramoleculares que le confieren estabilidad en el medio solvente. Aquí se observan las interacciones: (a) entre el oxígeno del grupo -COOH con el grupo metil vecino, (b) entre el átomo de hidrógeno entre el grupo -NH y el grupo -NH2 y (c) entre el grupo cetónico del anillo beta-lactámico con el hidrógeno del anillo aromático de la molécula. Adicionalmente, esta conformación C56 fue utilizada como configuración inicial con el puente de hidrógeno en el grupo -COOH y optimizada en el medio solvente. En la optimización con puente de hidrógeno intramolecular la ganancia en estabilidad energética fue de -18,99 kJ/mol. En las conformaciones con puente de hidrógeno se observa que la conformación C34 tiene la mayor energía de solvatación. En esta conformación, la amoxicilina está completamente plegada con los grupos -COOH, -NH2, -C=O y el anillo beta-lactámico expuestos para interaccionar con el agua descrito de manera implícita (ver Figura 6(h)). Adicionalmente, con este arreglo conformacional se observa una interacción intramolecular entre el anillo aromático y el azufre presente en el anillo de cinco miembros.
Finalmente, se puede decir que la conformación más estable en agua va a depender de la presencia o no del enlace de hidrógeno intramolecular en la molécula de amoxicilina.
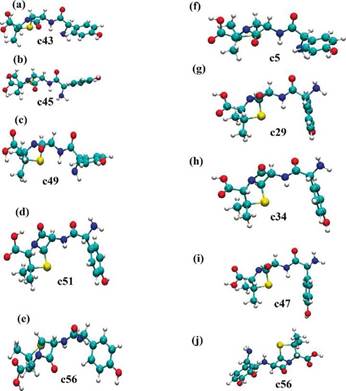
Figura 6 Conformaciones estructurales de la amoxicilina más estables en el agua descrita como solvente implícito. (a), (b), (c), (d) y (e) corresponden a las conformaciones C43, C45, C49, C51 y C56 sin el puente de hidrógeno intramolecular en el grupo -COOH. (f), (g), (h), (i) y (j) corresponden a las conformaciones C5, C29, C34, C47 y C56 con el puente de hidrógeno intramolecular en el grupo -COOH.
Análisis conformacional de la amoxicilina mediante la simulación de dinámica molecular
La dinámica molecular es un tipo de técnica computacional que ha permitido analizar el comportamiento o evolución de un sistema (físico, químico o biológico) a través del tiempo, calculando las fuerzas entre los átomos que lo conforman mediante las ecuaciones del movimiento de Newton. En este caso, la variación de la conformación espacial de la amoxicilina en presencia de agua definida de forma explícita fue evaluada usando la combinación de los Force Field OPLS-AA [46] y TIP4P [47], [48]. Estos modelos de Force Field han sido ampliamente aceptados para describir las propiedades estructurales y termodinámicas de moléculas orgánicas y agua en diferentes estudios computacionales. La molécula de amoxicilina que fue insertada en la caja con agua presentaba una conformación plegada como se observa en la Figura 3. De esta simulación de dinámica molecular se obtuvieron un total de 20.000 conformaciones espaciales para la molécula de amoxicilina en agua.
En esta primera parte, los cambios conformacionales con respecto a la estructura inicial fueron explorados para evaluar la variación estructural de la molécula de amoxicilina en el agua a lo largo de la simulación. Para realizar esto, la raíz cuadrada de la desviación cuadrática media de las posiciones de los átomos (RMSD) en el espacio ocupado fue determinada usando la trayectoria de las posiciones atómicas a lo largo del tiempo de simulación. La distribución de probabilidad de esta propiedad estructural se muestra en la Figura 7.

Figura 7 Distribución de probabilidad para el RMSD de la amoxicilina en agua obtenido con la simulación de dinámica molecular. 20000 conformaciones espaciales fueron obtenidas para la amoxicilina. Este valor de RMSD fue determinado usando una conformación plegada de la amoxicilina.
Como se observa en la Figura 7, las conformaciones espaciales obtenidas para la amoxicilina fueron plegadas, semiextendidas y extendidas completamente. En este caso, las conformaciones espaciales semiextendidas y extendidas de la amoxicilina están presentes con mayor proporción en el medio acuoso explícito en comparación con la conformación inicial tipo plegada. La conformación espacial semiextendida se presenta con la mayor probabilidad y un valor de RMSD de 0,26 nm, lo cual indica una gran variación conformacional de la estructura molecular de la amoxicilina en agua en comparación con la estructura inicial que fue colocada dentro de la caja de agua. En dicha conformación espacial, la amoxicilina se encuentra con todos los grupos funcionales expuestos al exterior para interaccionar con las moléculas de agua. En cambio, en la estructura con la conformación plegada se observa la interacción intramolecular entre el anillo aromático y el anillo de cinco miembros presente en la amoxicilina. De igual manera, en esta conformación se observa la interacción tipo puente de hidrógeno entre el átomo de hidrógeno del grupo -NH y el nitrógeno -NH2 presente en la estructura.
Adicionalmente, la distribución de probabilidad de la energía total de la molécula de amoxicilina para sus diferentes conformaciones en agua fue determinada en este estudio. Este resultado se muestra en la Figura 8.

Figura 8 Distribución de probabilidad de la energía total de la amoxicilina en agua obtenida de la simulación de dinámica molecular tipo NVT.
Como se muestra en la Figura 8, las energías totales de las conformaciones obtenidas de la simulación con dinámica molecular se encuentran en un intervalo comprendido entre -200 y -50 kJ/mol. El valor de energía total igual a -50 kJ/mol sugiere que el arreglo espacial extendido para la amoxicilina en agua corresponde a la conformación menos estable presente en el medio solvente. A su vez, la amoxicilina ligeramente plegada es la conformación espacial que tiene la mayor probabilidad de estar presente en el medio acuoso, lo cual indica que esta configuración tiene la población de conformaciones más alta a lo largo del proceso de simulación con un valor de energía total comprendido entre -130 y -100 kJ/mol. También, se puede observar que la conformación completamente plegada tiene la energía más estable (alrededor de -200 kJ/mol) en comparación con el resto de las conformaciones observadas en las simulaciones. En esta conformación plegada se observa que el anillo aromático interacciona con el anillo formado por cinco átomos y los grupos funcionales polares quedan expuestos para interaccionar con las moléculas de agua. Esto indica que se presenta el efecto hidrofóbico en este proceso de solvatación de la molécula de amoxicilina en la fase acuosa. Finalmente, los resultados obtenidos de la simulación de dinámica molecular sugieren que hay una considerable variación de las conformaciones de la amoxicilina a lo largo de la simulación. En este caso, el mayor RMSD fue obtenido para la conformación extendida; sin embargo, esta conformación corresponde a la conformación menos estable en el medio solvente desde el punto de vista energético. En cambio, el RMSD (alrededor de 0,1) de la conformación plegada fue el más bajo, lo cual indica que esta conformación es muy parecida a la conformación inicial usada para el proceso de simulación. En este estudio, usando la combinación de modelos de energía potencial OPLS-AA [46] y TIP4P [47], [48], la conformación plegada corresponde a la más estable como lo indica la energía total obtenida de la simulación. La ventaja que tiene el usar la dinámica molecular es que nos permite obtener un mayor conjunto de conformaciones espaciales en comparación con el obtenido con el programa Ballon-v1.8.2 [33]. Este criterio es importante siempre y cuando se utilice el modelo de energía potencial adecuado para describir las moléculas en estudio. En la siguiente sección se exploran las interacciones moleculares entre la amoxicilina y el agua que influyen en su conformación espacial en fase acuosa.
Evaluación de las interacciones moleculares entre la amoxicilina y el agua mediante dinámica molecular
Para evaluar las interacciones moleculares entre la amoxicilina y las moléculas de agua se utilizó la función de distribución radial (RDF, por sus siglas en inglés) que permite determinar las capas de solvatación alrededor de una molécula en particular y la intensidad de la interacción en un medio solvente. La curva RDF entre la amoxicilina y el agua en conjunto con una representación de las capas de solvatación se muestran en la Figura 9.
La curva RDF fue obtenida utilizando los centros de masas de las moléculas involucradas en este estudio. En la Figura 9(a) se observan un total de tres picos de máxima intensidad localizados a las distancias de 2,12; 5,80 y 8,40 Å. Estos picos indican la formación de tres capas de solvatación alrededor de la molécula de amoxicilina. La primera capa de solvatación tiene un espesor de 2,12 Å medido desde el centro de masa de la amoxicilina. La intensidad de este primer pico sugiere que la interacción molecular es muy débil entre las moléculas de agua localizadas en este radio de interacción y la amoxicilina. El número total de moléculas de agua localizadas en esta región es de 31 (ver Figura 9(b)). La segunda capa de solvatación empieza a una distancia 2,12 Á y termina en la posición del segundo pico de interacción a una distancia de 5,80 Å. Las moléculas de agua localizadas en esta capa de solvatación interaccionan con las moléculas de amoxicilina y con las moléculas de agua localizadas en la primera capa de solvatación que están interaccionando con la molécula de amoxicilina. Esta descripción ha sido utilizada en otros estudios de solvatación explícita [52], [53]. En este caso, las interacciones moleculares que prevalecen en esta región corresponden a los puentes de hidrógeno entre las moléculas de agua localizadas en esta región. Desde 5,80 hasta 8,40 Å se observa una tercera capa de solvatación alrededor de la molécula de amoxicilina que corresponde a la interacción tipo puentes de hidrógeno entre las moléculas de agua. El número de moléculas de agua alrededor de la segunda capa de solvatación fue de 90 moléculas según los resultados obtenidos de la simulación realizada (ver Figura 9(b)).

Figura 9 (a) Curva de la función de distribución radial entre la amoxicilina y el agua obtenida de la simulación de dinámica molecular tipo NVT y (b) Capas de solvatación alrededor de la molécula de amoxicilina.
De igual manera, la interacción molecular entre los grupos funcionales presentes en la amoxicilina con el agua fue evaluada mediante la función de distribución radial utilizando los últimos 10 ns de la simulación de dinámica molecular tipo NVT (ver Figura 10). Aquí se observa cómo los grupos funcionales -COOH, -NH2, -OH y -NH tienen la interacción molecular más fuerte con el agua en el proceso de simulación. En este caso, la fuerza de la interacción con el agua tiene el siguiente orden para los grupos funcionales evaluados: -NH2 > -OH > -COOH> -NH como lo expresa la magnitud del primer pico de interacción.
El pico de máxima intensidad para el grupo -COOH está localizado a una distancia de 3,04 Å. Este grupo funcional es un donador de protones. Este protón saliente de este grupo funcional puede ser aceptado por las moléculas de agua que rodean a la amoxicilina. En cambio, para los grupos -OH y -NH2, el pico de máxima intensidad está localizado a 2,80 Å. El grupo -NH2 tiene un par de electrones libres que lo convierten en un buen aceptor de los hidrógenos presentes en las moléculas de agua y el grupo funcional -OH puede ser solvatado muy bien por las moléculas de agua. La intensidad del pico del grupo -COOH es menor en comparación con el del grupo -NH2 y el grupo -OH. En este caso, se corrobora que estos grupos funcionales están asociados directamente a los pKa de la molécula de amoxicilina debido a que presentan los picos de interacción de mayor intensidad en la curva de RDF que se muestra en la Figura 10.

Figura 10 Curva de la función de distribución radial entre los grupos funcionales presentes en la amoxicilina y el agua, obtenida de la simulación de dinámica molecular tipo NVT.
En función de la curva RDF, se puede establecer que los grupos funcionales: -NH2, -OH y -NH presentes en la amoxicilina tienen una solvatación más efectiva en agua en comparación con el grupo funcional -COOH. También se observa que el anillo beta-lactámico tiene dos picos de interacción débil con intensidades localizadas en las posiciones 4,54 y 7,44 Å. Esto sugiere la presencia de dos capas de solvatación alrededor de este anillo que permite indicar la exposición que tiene esta porción de la molécula de amoxicilina a las moléculas de agua. Adicionalmente, la función de distribución espacial (SDF, por sus siglas en inglés) alrededor de la molécula de amoxicilina fue determinada con la simulación de dinámica molecular [54], [55]. Esta función muestra la isosuperficie que producen las moléculas de agua alrededor de la molécula de amoxicilina. En este caso, la isosuperficie SDF fue obtenida usando como grupo funcional de referencia el -COOH presente en la amoxicilina, como se muestra en la Figura 11.
En la Figura 11 se observan las isosuperficies que corresponden a la capa de solvatación alrededor de los diferentes grupos presentes en la estructura de la amoxicilina. Estas isosuperficies están localizadas en las regiones más hidrofílicas que se muestran en la estructura de la amoxicilina en dicha conformación espacial promedio [52]. Esto indica que las moléculas de agua rodean de forma efectiva los grupos polares presentes en la molécula de amoxicilina. En la Figura 11(a) se muestra cómo la isosuperficie SDF está localizada en la región asociada al grupo -COOH cuando la referencia para determinar dicha propiedad es el mismo grupo funcional. En la Figura 11(b) se observa cómo la isosuperficie cubre completamente a la molécula de amoxicilina cuando la referencia utilizada para su estimación fue el grupo funcional -NH2 y finalmente para el grupo -OH usado como referencia se observa que la capa de solvatación se concentra de igual manera en la región más hidrofílica de la molécula (ver Figura 11(c)). En este caso, se observa que el anillo aromático no muestra isosuperficies SDF cuando las moléculas de agua están cerca de su entorno. Para complementar lo obtenido en esta distribución de moléculas de agua alrededor de la estructura molecular de la amoxicilina, la energía de solvatación y la superficie accesible al solvente fueron determinadas para esta molécula en el medio solvente [56], [57]. En la Figura 12 se muestra la energía libre de solvatación y la superficie accesible al solvente como función del tiempo de la simulación de dinámica molecular.
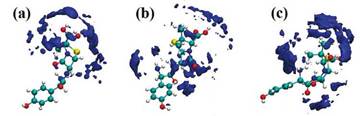
Figura 11 Representación de la función de distribución espacial (SDF, por sus siglas en inglés) del sistema amoxicilina y agua obtenido del análisis de la simulación de dinámica molecular tipo NVT. La SDF fue determinada usando diferentes referencias: (a) grupo funcional -COOH, (b) grupo funcional NH2 y (c) grupo funcional -OH.
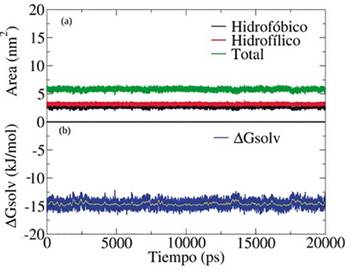
Figura 12 (a) Área accesible al solvente de la amoxicilina como función del tiempo de simulación y (b) Energía libre de solvatación de la amoxicilina en agua como función del tiempo de simulación.
Claramente, como se muestra en la Figura 12(a) la región hidrofílica tiene más área de contacto con el agua en comparación con la región lipofílica. El área accesible al solvente para la región lipofílica de la molécula es de 2,63±0,17 nm2 y para la región hidrofílica el área accesible fue de 3,18±0,23 nm2. Estos valores indican que la región hidrofílica es la que presenta los grupos funcionales -COOH, -NH2 y -NH en conjunto con el anillo beta-lactámico contenido en la estructura de la amoxicilina. Finalmente, el valor de -14,58 kJ/mol para la energía libre de solvatación muestra la afinidad que tiene la molécula de amoxicilina por el agua. Sin embargo, este valor es muy bajo comparado con los reportados por Khanal y Adhikari [58], comprendido entre -528 y -558 kJ/mol, el cual fue obtenido por simulaciones de dinámica molecular usando diferentes modelos de energía potencial para describir el agua y distintos métodos de integración para calcular la energía libre de solvatación. Cabe destacar que el valor obtenido en este trabajo sugiere que la molécula de amoxicilina tiene una alta solubilidad en agua a una temperatura de 298,15 K (ver Figura 12(b)). La solubilidad experimental de la amoxicilina en agua ha sido reportada con un valor aproximado de 4 mg/mL [59], [60]. Finalmente, esto indica que los resultados de las simulaciones moleculares son consistentes con los valores reportados experimentalmente.
Conclusiones
El arreglo espacial y la interacción molecular de la amoxicilina en agua fueron evaluados mediante dos estrategias de simulación molecular. Inicialmente, el generador de conformaciones espaciales balloon-v-1.8.2 que depende del modelo de energía potencial MMFF94 fue usado para construir las conformaciones de la amoxicilina, y la estabilidad de las conformaciones de esta molécula fue determinada mediante cálculos mecánico-cuánticos en el vacío y en el solvente con el método de solvatación implícita. Los resultados han demostrado que no es adecuado considerar las conformaciones obtenidas por el generador de conformaciones como geometrías aceptables, sino que es necesario hacer una exploración de estas configuraciones usando los cálculos mecánico-cuánticos. Para la amoxicilina se obtuvo que la conformación más estable en el vacío (conformación C1) difiere de la obtenida en el medio solvente (conformación C56). Particularmente, los cálculos mecánico-cuánticos en el vacío sugieren que la amoxicilina tiene una conformación extendida. Sin embargo, usando la solvatación implícita, la amoxicilina tiene un arreglo semiplegada y plegada completamente para la conformación sin puente de hidrógeno y con puente de hidrógeno en el grupo -COOH. La presencia del puente de hidrógeno intramolecular contribuye a incrementar la estabilidad de la molécula en el medio solvente. De la simulación de dinámica molecular, la amoxicilina es bien descrita por el modelo de energía potencial OPLS-AA. En este caso, los resultados sugieren que la conformación más estable en agua corresponde a una conformación plegada. Sin embargo, en la simulación, la conformación con mayor población presente es la conformación semiplegada. De igual manera, la RDF indica que la amoxicilina presenta tres capas de solvatación alrededor de su estructura molecular. La función de densidad espacial y la superficie accesible al solvente sugieren que la amoxicilina tiene una región hidrofílica bien definida en donde se encuentran presentes el anillo beta-lactámico y los grupos -COOH, -NH2 y -NH. La energía libre de solvatación de -14,58 kJ/mol indica que la amoxicilina tiene una muy buena afinidad por el agua. Sin embargo, este valor difiere considerablemente del obtenido por el método de solvatación implícita de -98,16 y -121,42 kJ/mol para las conformaciones más estables. En este trabajo, ambas estrategias de cálculos permiten explicar el comportamiento de las conformaciones de la amoxicilina en agua.

















