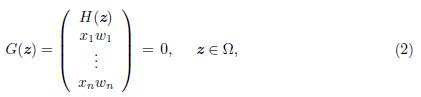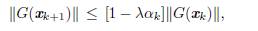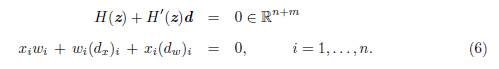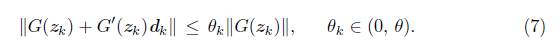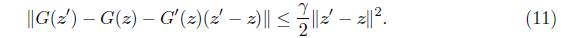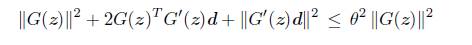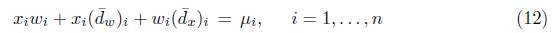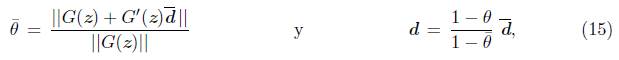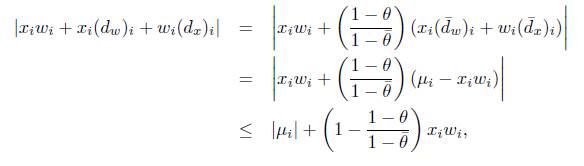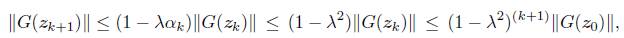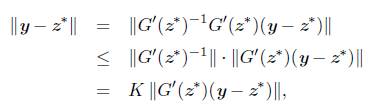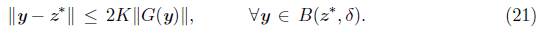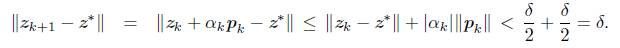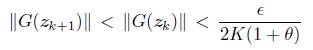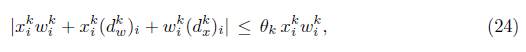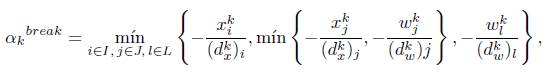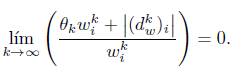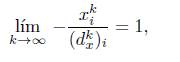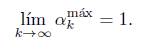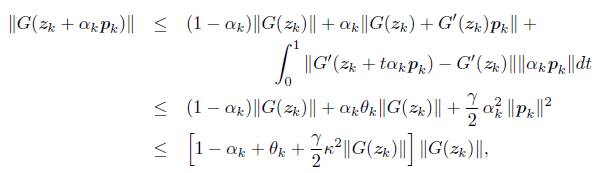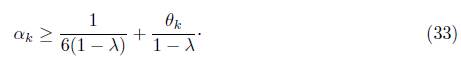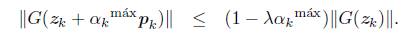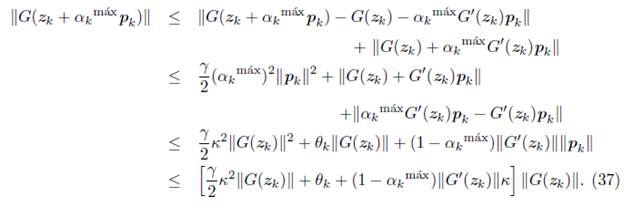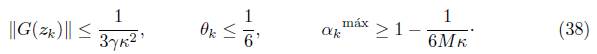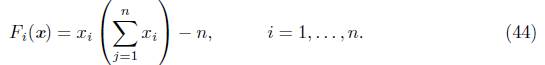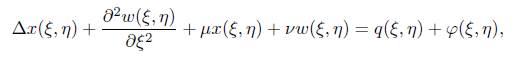Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introducción
Dada una función H: ℝ n+m+n -y ℝ n+m continuamente diferenciable, el Problema de Complementariedad Horizontal, abreviadamente PCH(H), consiste en encontrar vectores x Є ℝ n, y Є ℝ m y ω G Rn tales que
En este contexto, decimos que un vector es no negativo, si todas sus componentes son no negativas.
Observemos que, en el problema PCH(H), no hay restricciones sobre el vector y. En algunos casos este vector no existe, por ejemplo cuando H(x, w) = F(x) - ω, para cualquier función F: ℝ n - ℝ n no lineal y continuamente diferenciable, con lo cual el problema de complementariedad horizontal, se reduce al bien conocido problema de complementariedad no lineal, que consiste en hallar x G Rn tal que
Otros problemas relacionados con el de complementariedad horizontal son los de comple-mentariedad Lineal [10], implícita [27], vertical [9] [14] y, desigualdades variacionales [15] [21]. Para estos problemas han sido propuestos, entre otros, métodos tipo [3] [10] Newton [8] [12] [16] [23] [22] [30] [31], Newton inexacto [13] [17] [18] [27] [29] [33] y cuasi-Newton inexacto [7].
Las numerosas aplicaciones del problema en áreas como ingeniería, economía, modelos de equilibrio, teoría de optimización [5], [14], [19], [28], [32] han incrementado el interés de investigadores en proponer algoritmos eficientes para su solución [6], [2], [24], [26].
Una estrategia muy usada para resolver el problema de complementariedad horizontal, consiste en reformularlo como el siguiente sistema de ecuaciones no lineales restricto
donde G: ℝ n+m+n -y ℝ n+m+n y Ω= { z = (x, y, ω) Є ℝ n+m+n : x ≥ 0 , ω ≥ 0}.
A su vez, y con el objetivo de proponer algoritmos globales para su solución (e indirectamente resolver el problema de complementariedad horizontal), el sistema (2) puede reformularse como el siguiente problema de minimización
donde || • || denota la norma euclidiana.
En [4], los autores resuelven (3) mediante un algoritmo global de punto interior con direcciones Newton inexactas, el cual preserva factibilidad mediante el uso de gradientes proyectados. La demostración de convergencia (lineal, superlineal y cuadrática) de dicho algoritmo es presentada en [6]. Por otra parte, en [1], los autores demuestran que el uso de direcciones de Newton exactas en el algoritmo propuesto en [4] tiene buenas propiedades locales de convergencia.
Recientemente, en [7], el autor presenta un nuevo algoritmo global cuasi Newton inexacto de punto interior para resolver problemas de complementariedad horizontal basado en la reformulación (3). Este algoritmo usa, siempre que sea posible, una dirección cuasi-Newton inexacta y en algunas iteraciones, para garantizar factibilidad, proyecta dicha dirección sobre el conjunto Ω. Con esta estrategia, se mantienen buenas propiedades de convergencia de los métodos cuasi-Newton.
Motivados por los buenos resultados obtenidos en [7], en este artículo, usamos la estrategia de combinar una dirección Newton inexacta con su proyección sobre el conjunto Ω, solo cuando se necesite garantizar factibilidad, para proponer un nuevo algoritmo tipo Newton inexacto par resolver el PCH(H) indirectamente a través de su reformulación como el problema de minimización (3). Vale la pena mencionar que este nuevo algoritmo usa una estrategia de búsqueda lineal diferente a la utilizada en [7], la cual resultó más eficiente numéricamente. Complementamos la nueva propuesta algorítmica con su análisis teórico y numérico.
Organizamos la presentación de este artículo en la siguiente forma. En la Sección 2, presentamos el nuevo algoritmo y describimos algunas de sus características. En la Sección 3, presentamos el análisis de convergencia del algoritmo propuesto. En la Sección 4, analizamos su comportamiento numérico. Finalmente, en la Sección 6, presentamos algunos comentarios finales.
2. Nuevo algoritmo
En esta sección, presentamos un nuevo algoritmo global de punto interior para resolver (3), el cual genera una sucesión de puntos factibles {x k } que satisface la condición de decrecimiento suficiente [24],
donde α
k
es el tamaño del paso y
. Esta condición es libre de derivadas, lo cual es ventajoso en lo que respecta al costo operacional del algoritmo. Además, su uso se justifica por su relación con algoritmos tipo Newton inexactos globalmente convergentes, en los cuales se exige, en cada iteración, un decrecimiento suficiente de ||G|| [11].
Una característica importante del nuevo algoritmo es su búsqueda direccional, la cual usa una dirección Newton inexacta, a menos que se pierda factibilidad, caso en el cual, se proyecta esta dirección sobre el conjunto Ω .
Antes de presentar el algoritmo y para una mejor comprensión del mismo describimos explícitamente la matriz jacobiana de G en z, denotada G'(z) Є ℝ ( n+m+n)x(n+m+n) y el sistema de ecuaciones lineales G(z) + G''(z)d = 0.
donde H'(z) Є ℝ (n+m)x(n+m+n) es la matriz jacobiana de la función H en el vector z; W = Diag(w 1 ,... ,w n ) Є ℝ nxn ; X = Diag(x 1 ,... ,x n ) Є ℝ nxn y 0 denota la matriz cero en R mxm .
Usando (4) y un vector d = (d x d y d w ) T Є ℝ (n+m+n) , el sistema G'(z)d = -G(z) equivalentemente G(z) + G'(z)d = 0 puede expresarse como el sistema matricial,
el cual, después de unos sencillos cálculos matriciales se convierte en el siguiente sistema de n + m + n ecuaciones no lineales,
La estructura del sistema (5) y en particular, del sistema (6) desempeña un papel central en nuestra propuesta algorítmica.
Debido a que el algoritmo propuesto es tipo Newton inexacto con direcciones proyectadas, lo llamaremos Algoritmo NIDP. Presentamos a continuación su descripción formal.
Algoritmo (Algoritmo NIDP).
Sean
, y c
small
< 1. Para k = 0,1, hacer:
1. Criterio de parada. Si ||G(zk)|| ≤ ε pare. Sino, siga los pasos 2 a 6.
2. Dirección de Newton inexacta. Calcule
tal que
Si ||d k ||\ ≤ c big y
entonces defina p k = d y sino, pase al Paso 4.
3. Tamaño de paso máximo. Dado T k Є [t, 1), calcule (7)
y haga
pase al Paso 4, de lo contrario, pase al Paso 5.
4. Direcciones proyectadas. Escoja T k Є [t, 1), haga α k = T k y defina
4.1. Si ||G(z k + α k p+)|| ≤ [1 − λα k ]||G(z k )|| defina p k = p+ y pase al Paso 6.
4.2. Si z k + α k p− ∈ Ω y || G(z k + α k p−)|| ≤ [1 − λα k ]||G(z k )||defina p k = p− y pase al Paso 6.
4.3. Haga α k = β αk y vuelva a 4.1.
4.4. Si α k = λ, pare.
5. Búsqueda lineal. Calcule
tal que
5.1. Si α k = λ, pare.
6. Actualización. Haga zk+i = z k + α k P k .
Observe que en el Paso 4, se calcula no solamente p+, sino su negativo, pero solo se pregunta por la factibilidad de p debido a que, este vector no necesariamente es factible.
3. Análisis de convergencia
En esta sección, presentamos los resultados de convergencia del Algoritmo NIDP. Las hipótesis generales que usamos en el análisis son las siguientes.
H1. Existe z* Є Ω tal que G(z*) = 0.
H2. G(z) es una función Lipschitz continua en Ω. Es decir, existe una constante positiva Υ tal que, para todo z, z’ Є Ω,
Una consecuencia inmediata de la hipótesis H2 es que para todo z, z’ Є Ω,
El siguiente teorema garantiza que una dirección de Newton inexacta es de descenso para la función de mérito f.
Teorema 3.1. Si G(z) = 0 y d es una dirección que satisface (7), para algún θ Є [0,1), entonces
Demostración. Si d es una dirección que satisface (7) entonces
por lo tanto,
de donde,
luego,
y como 0 ≤ θ < 1, concluimos que
Por otro lado, es claro que si ∇ f (z) T p+ = 0 entonces p+ o p_ será una dirección de descenso para f . Lo anterior nos permite inferir que en cualquier caso, los ciclos en 4.1, 4.2 o en el Paso 5 terminarán en un número finito de repeticiones.
El siguiente teorema da una condición suficiente que garantiza la existencia de una dirección tipo Newton que cumple las condiciones (7) y (8).
Teorema 3.2. Sea z Є Ω tal que G(z) = 0. Si un vector no nulo d satisface
Y
entonces existe θ min Є [0, 1) tal que, para cualquier θ Є [θ min , 1), existen d Є Rn+m+n y η Є [0, 1) tales que
Y
En particular, si
entonces, para cualquier θ Є [0,1), existe d Є ℝ n+m+n
tal que (13) se cumple y además,
Demostración. Para d = 0, sean
con θ Є [9,1). Usando (15) tenemos que
Usando
en la desigualdad anterior, concluimos que
Si definimos
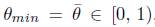, tenemos que existe d dada en (15) tal que (13) se satisface. Además, para este vector, por (12), se satisface que
por tanto, existe
tal que d Є ℝ
n+m+n
satisface (14). Finalmente, supongamos que
Luego, para
se verifican (5) y (6), con lo cual
. Además, de (15) y (16)
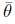= 0, y con ello, η = 9. Así, para cualquier 9 G [0,1), existe d Є ℝ n+m+n tal que (13) se satisface y, además,
Observe que si G'(z) es no singular entonces, tomando
, podemos garantizar que (16) se cumpla y por tanto, que exista una dirección d que satisfaga (7) y (8) para cualquier θ Є [0,1).
El siguiente teorema garantiza que la sucesión de imagenes de los puntos generados por el Algoritmo NIDP converge a cero.
Teorema 3.3. Si {z k } es una sucesión generada por el Algoritmo NIDP, entonces
Demostración. Sean p k una dirección calculada mediante el paso 2 o el paso 4 y a k G (0, 1) el tamaño del paso calculado en las búsquedas lineales llevadas a cabo en los pasos 4.1, 4.2 o 5. Luego,
dado que
, concluimos que
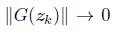siempre que k → ∞, con lo cual obtenemos el resultado deseado.
La no singularidad de la matriz jacobiana de G en un punto de acumulación de una sucesión generada por el Algoritmo NIDP es suficiente para garantizar, no solo la convergencia de la sucesión a dicho punto, sino también que ese punto es una solución del sistema de ecuaciones no lineales (2). Esto lo garantiza el siguiente teorema.
Teorema 3.4. Si {z k } es una sucesión generada por el Algoritmo NIDP y z* es un punto de acumulación de la sucesión tal que G'(z*) es no singular entonces
Demostración. Por hipótesis, z* es un punto de acumulación de {z k }. Entonces existe una subsucesión {z kj } tal que z kj → z*, cuando j → ∞ y, por la continuidad de G,
Además, el Teorema 3.3 garantiza que G(z k ) → 0, cuando k → ∞, por lo tanto, G(z*)=0.
Por otra parte, sean K = ||G'(z*) -1 || y 6 un escalar positivo suficientemente pequeño1 tales que, para todo y Є B(z*, δ) se cumplen las tres condiciones siguientes:
i) Existe la matriz G'(y) -1 ;
2i) ||G'(y) -1 || < 2K; y
3i)
.
Ahora, para y Є B(z*, δ) tenemos que,
Para acotar el primer término del lado derecho de (19), observemos que
con lo cual
de (19) y (20),
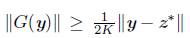equivalentemente
Sean e 1 Є (0, δ/8) y Є = mín{Є 1 , c big }. Como z* es un punto de acumulación de {z k } y G(z*) = 0, entonces existe un k suficientemente grande tal que
Por i) y el Teorema 3.2 tenemos que, para tal k y cualquier θ Є (0, 1), existe una dirección d k tal que (7) y (8) se satisfacen. Así,
dado que, Є < δ/8 entonces || d k || < δ/2.
Ahora, si α k max ≤ c small en el Paso 3 del algoritmo entonces d k será proyectada, y por propiedades de la proyección,
Así, en cualquiera de los casos en que sea calculada la dirección p k , se tiene que ||p k || ≤ δ/2 con lo cual,
Luego, z k + 1 Є B(z*,δ). Por otra parte,
y por (21)
concluimos que
por lo tanto, z k + 1 Є S Є .
En resumen, para todo k mayor que un k suficientemente grande, se cumple que z k Є S e y como ||G(zk)|| → 0, de (21), concluimos que z k → z*, cuando k → ∞.
Una consecuencia del Teorema 3.4, es que la sucesión {||p k ||} está acotada. Esto se formaliza en el Corolario 3.5.
Corolario 3.5. Si {zk} es una sucesión generada por el Algoritmo NIDP y z* es un punto de acumulación de la sucesión tal que G (z * ) es no singular, entonces existen una constante k > 0 y un k tal que para todo k ≥ k, se cumple que
Demostración. Por el Teorema 3.4, z k → z* cuando k → ∞, luego existe un k suficientemente grande tal que para todo k ≥ k, se tiene que z k Є B(z * , δ), donde δ es la constante positiva que garantiza las condiciones i) a 3i) en la demostración anterior. Por i), (22) y (23), para todo k ≥ k, se satisface la desigualdad
Por lo tanto, para todo k ≥ k, existe k = 4K tal que
La constante k del corolario anterior proporciona una cota inferior para la constante c big de algoritmo propuesto, bajo la cual la dirección de Newton será aceptada. Así lo garantiza el siguiente corolario.
Corolario 3.6. Bajo las hipótesis del corolario anterior, si, Cb ig > 4K entonces existe k tal que para todo k > k la dirección de Newton inexacta, calculada en el Paso 2 del algoritmo será aceptada.
En el siguiente teorema se garantiza que la sucesión {α b k reak }, cuyos términos ayudan a obtener el tamaño de paso máximo, converge a uno.
Teorema 3.7. Sea {zk} una sucesión generada por el Algoritmo NIDP. Si z* Є Ω es un punto de acumulación de dicha sucesión, la matriz G'(z*) es no singular, C big ≥ 4K y θ k - 0 entonces
Demostración. Por el Teorema 3.4, la sucesión {z k } converge a z* y por hipótesis, c big ≥ 4K, con lo cual el Corolario 3.6 garantiza que la dirección d k calculada en (7) será aceptada en el paso 2 del algoritmo.
Ahora, como la matriz G (z * ) es no singular entonces existe k tal que G’ (zk) es no singular para todo k ≥ k, lo que a su vez implica de acuerdo con (4) que x i k y w i k no se anulan simultáneamente. Sin pérdida de generalidad, supongamos x i k > 0, para todo i = 1,.. . ,n.
Por (8),
luego,
dado que, xik > 0 y wik ≥ 0 entonces (dkX)i y (dkw )i no pueden ser simultáneamente no negativos. En particular, no es posible que (dkX)i = 0 y (dkw)i > 0 o viceversa. Por tal razón, consideramos los siguientes casos:
Caso 1: (dkx)i = (dkw)i = 0.
Caso 2: (dkx)i < 0 y (dkw)i ≥ 0.
Caso 3: (dkx)i < 0 y (dkw)i < 0.
Caso 4: (dkx)i ≥ 0 y (dkw)i < 0.
Si el Caso 1 ocurre para todos los índices i, entonces la iteración actual es solución del problema. Por lo tanto, supondremos que los casos 2, 3 o 4 ocurren por lo menos para algún índice i. Por (9) inferimos que abreakk debe ser tal que
Luego,
• Si i es un índice para el cual el Caso 1 ocurre, entonces (26) será satisfecho por cualquier αkbreak ≥ 0.
• Si i es un índice para el cual el Caso 2 ocurre, entonces (26) será satisfecho siempre que
Como αkbreak debe satisfacer (27), (28) y (29) simultáneamente, entonces
donde I, J y L denotan los conjuntos de índices para los cuales, ocurren los casos 2, 3 y 4, respectivamente.
Observe que en los casos 3 y 4 wik = 0, en caso contrario (24) implica que (dkW )i = 0, lo cual no es posible. Por otra parte, como la matriz G (z*) es no singular entonces, por el Teorema 3.4, G( z* ) = 0. Luego, por las condiciones de complementariedad y no negatividad, xi* = 0 o ωi* = 0. Además, por la no singularidad de G ( z* ) y de acuerdo con su estructura, deducimos que xi* y wi* no se pueden anular simultáneamente. Nuevamente, sin pérdida de generalidad, supongamos xi* = 0.
Dado que wik → wi* = 0 y por el Corolario 3.5 existe una constante k > 0 tal que ||dk|| ≤ K||G(zk)|| entonces
Así, para k suficientemente grande, podemos asumir que
Ahora, por (8) concluimos que
Luego,
Nuevamente, por el Corolario 3.5, para k suficientemente grande existe una constante k tal que ||dk|| ≤ K||G(zk)|, luego (dW)i| ≤ K||G(zk)|| y como G(zk) → 0, podemos concluir que |(dkw)i| → 0. Por otro lado, para los casos 3 y 4, tenemos que wik → w* = 0 y dado que θk → 0 entonces
Luego, de (31) deducimos que xik + (dkx)i = o(xik). En consecuencia,
lo cual completa la prueba del teorema.
Dos consecuencias del Teorema 3.7 son los dos corolarios siguientes. El primero garantiza que la dirección de Newton inexacta generada por el Algoritmo NIDP será aceptada como dirección de descenso; el segundo, que la sucesión {αkmax} de tamaños máximos del paso, converge a uno.
Corolario 3.8. Sea {zk} una sucesión generada por el Algoritmo NIDP. Si z* es un punto de acumulación de la sucesión tal que G (z*) es no singular, cbig > 2K y θk → 0 entonces existe un k tal que para todo k ≥ k la dirección de Newton inexacta calculada en el Paso 2 del algoritmo será aceptada como dirección de descenso.
Corolario 3.9. Sea {zk} una sucesión generada por el Algoritmo NIDP. Si z* Є Ω es un punto de acumulación de dicha sucesión, G'(z*) es no singular, Cbig ≥ 4K, θk → 0 y Tk → 1, k → ∞ entonces
El siguiente teorema garantiza la convergencia superlineal de la sucesión generada por el algoritmo propuesto.
Teorema 3.10. Suponga la hipótesis H2 y sea {zk} una sucesión generada por el Algoritmo NIDP. Si z* Є Ω es un punto de acumulación de dicha sucesión, G'(z*) es no singular, Cbig ≥ 4K, Tk → 1, y θk → 0 entonces, para k suficientemente grande αk = αkmáx y además, {zk} converge superlinealmente a z*.
Demostración. Por el Corolario 3.8, Pk = dk para todo k suficientemente grande. Ahora,
Por tanto, y dado que αk Є (0,1), ||Pk|| < K||G(zk)|| y la hipótesis H2,
pero G(zk) → 0 entonces, en particular,
, para k suficientemente grande. Luego,
. Observemos que
siempre que (1 - λ)αk ≥ 1/6 + θk, dado que λ Є (0, 2/3) entonces para garantizar que (32) se cumpla, es suiciente que
Ahora, por el Corolario 3.9, sabemos que αkmax → 1 y como por hipótesis θk → 0 entonces, para k suficientemente grande, αkmax satisface (33) y por tanto, (32) de tal manera que
Luego, αkmax satisface la condición (10) en el Paso 5 del algoritmo en consecuencia, αk = αkmax, para k suficientemente grande.
Por otro lado, dado que G(z*) es no singular entonces G'(zk) es no singular y además, ||G'(zk)-1||≤ 2||G'(z*)-1|| = 2K, para k suficientemente grande, de donde
Por el Teorema del Valor Medio, sabemos que existe £k en el segmento que une a zk con z* tal que ||G(zk)|| = ||G(zk) - G(z*)|| ≤ ||G' (ξk)|| ||zk - z*||, pero como zk → z* y G' es continua, podemos asegurar que existe una constante R > 0 tal que, para k suficientemente grande, ||G'(ξk)|| ≤ R. Así,
Por (34) y (36),
con lo cual, garantizamos la convergencia superlineal de la sucesión ya que, zk → z*, θk → 0 y αk máx → 1. 0
Finalmente, el siguiente teorema garantiza la convergencia cuadrática de la sucesión generada por el algoritmo propuesto.
Teorema 3.11. Suponga la hipótesis H2 y sea {zk} una sucesión generada por el Algoritmo NIDP. Si z* Є Ω es un punto de acumulación de dicha sucesión, G'(z*) es no singular, Cbig ≥ 4K, y además suponga que existen constantes c1 y c2 tales que
entonces la sucesión {zk} converge cuadráticamente α z*.
Demostración. Por el teorema anterior, αk = αkmax para todo k suficientemente grande. Además, existe una constante k > 0 tal que ||pk|| ≤ k ||G(zk)||, y por (11), tenemos que
Dado que G es continuamente diferenciable y zk → z* entonces existe una constante M > 0 tal que ||G'(zk)|| ≤ M, para todo k suficientemente grande. De igual forma, como G(zk) → 0, αkmáx → 1 y θk = O (||G'(zk)||) entonces, para todo k suficientemente grande, se cumple que
Usando (38) en (37), se obtiene la siguiente desigualdad,
Por otro lado, sumando y restando algunos términos, usando la desigualdad triangular, el Paso 6 del Algoritmo propuesto, el hecho de que αkmáx ≤ 1 y la desigualdad (23), tenemos que
Luego, de (39),
Por lo tanto,
Así, de (37), (40) y dado que,||G′(zk)||≤ M, tenemos que
Finalmente, si c máx{c1,c2}, entonces por hipótesis
Usando (42) en (41),
.
Por (36), tenemos que
por lo tanto, la sucesión {zk} converge cuadráticamente α z*.
4. Experimentación numérica
En esta sección analizamos numéricamente el desempeño del Algoritmo NIDP. Para ello, usamos un computador con procesador Intel(R) Core(TM) i7, RAM de 16 GB y el software MATLAB para escribir los códigos de los algoritmos y funciones de prueba.
Usamos el criterio de parada ||G(z)||≤ ε = 10-6 y los siguientes valores para los parámetros del algoritmo, cbig = 104, csmall = 10-4 β = 0.5 X = 10-4 Tk = t = 0.9995, y N = 200. Además, usamos gradientes conjugados cuadrados (cgs), para calcular la dirección tipo Newton inexacta en el Paso 2 del algoritmo.
Consideramos tres problemas de complementariedad horizontal, dos de los cuales corresponden al caso particular de complementariedad no lineal. Con el fin de comparar los resultados obtenidos al resolver estos problemas con el Algoritmo NIDP, resolvemos los mismos problemas, con la versión exacta de este algoritmo (la dirección de descenso del Paso 2, se obtiene de forma exacta) que llamaremos Algoritmo NE, con el Algoritmo PGIN de [6] y con el Algoritmo CNIDP propuesto en [7].
Las tablas en las que reportamos los resultados contienen la siguiente información: tipo de algoritmo usado para la resolver el problema (Método), tamaño del problema (n), número de iteraciones realizadas por los algoritmos hasta encontrar una solución o converger a un punto estacionario (k), tiempo en segundos requerido por los métodos en caso de convergencia (t), número de iteraciones en las que se usó una dirección proyectada (Proy.), número de iteraciones internas que realizó el método inexacto (It.In.), punto inicial (zo), divergencia (--) y cociente de los errores entre dos iteraciones sucesivas RelRes = ||zk+1 - z*||/||zk - z*||.
4.1. Problema 1
El primer problema, es de complementariedad no lineal, y está asociado a la función F : ℝ n → ℝ n, definida por [20]
con, x0 = xn+1 = 0. Este problema es equivalente al de complementariedad horizontal, H(x, ω) = 0, xT ω = 0, x, ω ≥ 0, con H(x, ω) = F(x) - ω.
El Cuadro 1 contiene los resultados obtenidos al resolver este problema variando su tamaño y tomando como punto inicial un vector de unos del tamaño apropiado.
En general, el número de iteraciones del Algoritmo NIDP es mayor que el requerido por el Algoritmo NE, no obstante el tiempo de ejecución del primero es mucho menor que el del segundo, como es de esperarse. Resaltamos que el Algoritmo NE no requirió proyectar ninguna dirección, sin embargo, aunque el Algoritmo NIDP proyectó en todos los ensayos algunas de las direcciones, su eficiencia en términos de tiempo es indiscutible. En este mismo sentido, se puede observar que aunque el Algoritmo CNIDP es un algoritmo cuasi Newton, este fue menos eficiente en términos de tiempo, que el Algoritmo NIDP, lo cual sugiere un mejor rendimiento de la búsqueda lineal propuesta para el Algoritmo NIDP.
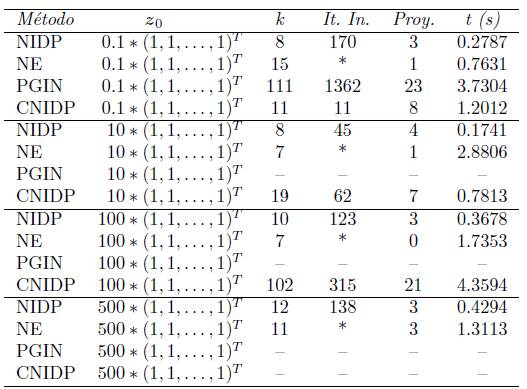
Por otro lado, con el fin de analizar el carácter global del Algoritmo NIDP, consideramos vectores iniciales múltiplos del vector de unos, y generamos 500 vectores iniciales aleatorios. El Cuadro 2 contiene los resultados obtenidos en el primer caso. Vale la pena mencionar que en todos estos experimentos el tamaño del problema fue n = 1000.
Los resultamos de el Cuadro 2 muestran la robustez del Algoritmo NIDP frente a los otros dos métodos.
Al resolver el Problema 1, con el Algoritmo NIDP y 500 puntos iniciales aleatorios, cuyas componentes se encuentran en el intervalo [0, 20], observamos que el método convergió en todos los experimentos con un promedio de 20.26 iteraciones y 0.3330 segundos. Entre tanto, el Algoritmo NE convergió en un promedio de 17.7 iteraciones y 1.1716 segundos. Estos resultados nuevamente, nos permiten resaltar la robustez del Algoritmo NIDP y su eficiencia en términos de tiempo del mismo.
Para finalizar los experimentos llevados a cabo con el Problema 1, presentamos en el Cuadro 3, el comportamiento detallado del Algoritmo NIDP para el problema de tamaño 1000 y z0 = (1,..., 1)T.
Como podemos observar, este experimento evidencia los resultados demostrados en la teoría de convergencia, en particular que el cociente RelRes, converge a cero, a medida que θ tiende a cero, lo que muestra en la práctica convergencia superlineal del algoritmo.
4.2. Problema 2
Este problema corresponde al de cornpleirientariedad no lineal (equivalentemente a uno de coniplernentariedad horizontal) asociado a F : ℝ n → ℝ n, definida por
El Cuadro 4 contiene los resultados obtenidos al resolver el Problema 2, con los Algoritmos NIDP, NE, PGIN y CNIDP a partir de z0 = (25, ..25)T. La segunda columna (n), indica el tamaño del problema. Como era de esperarse, debido a que la matriz jacobiana involucrada en este problema es densa, los métodos inexactos fueron más eficientes, en términos de tiempo, que su contraparte exacta. En particular, cuando el tamaño del problema fue considerablemente grande. Además, en la mayoría de experimentos, el Algoritmo NIDP fue más rápido y requirió de menos iteraciones que sus homólogos, el PGIN y el CNIDP.
Para analizar la robustez del Algoritmo NIDP, realizamos 1000 experimentos generando aleatoriamente puntos iniciales, con componentes en el intervalo [1, 50]. El porcentaje de éxito fue del 100% al resolver el respectivo problema de tamaño 1000. El algoritmo realizó en promedio 10 iteraciones y requirió aproximadamente de 0. 5 segundos para resolver el problema en cada uno de los experimentos.
El Cuadro 5, en sus columnas 2 a 6, contiene el valor de los parámetros del Algoritmo NIDP en cada una de las 11 iteraciones (columna 1) que demoró para resolver el Problema 2, con n = 1000 y z0 = (25, 25, ..., 25)T. Observamos muy buen desempeño, ya que en todas las iteraciones se dieron pasos completos. En la columna 6, se aprecia que el cociente RelRes, converge a cero, a medida que 0 tiende a cero (columna 5), lo cual evidencia la convergencia superlineal método, como se demostró en el Teorema 3.10.
4.3. Problema 3
Consideramos el problema de complementariedad horizontal, definido por
donde A,B Є ℝ nxn, q Є ℝ n y φ: ℝ n x ℝ n - Rn es un término no lineal. Estos problemas surgen de la discretización de una ecuación diferencial como la siguiente
con algunas condiciones de frontera y de complementariedad [25]. En la experimentación numérica usamos los parámetros establecidos en [25],
, con i y v constantes positivas,
tridiagonal por bloques, cuyas diagonales superior e inferior contienen, en cada uno de sus bloques la matriz -Im, con m2 = n, y cuya diagonal principal contiene en cada bloque la matriz S = tridiag( - 1, 4, - 1), de orden m. De igual forma,
donde ⊗ denota el producto de Kronecker.
Consideramos tres términos no lineales, también propuestos en [25] que dieron lugar a tres problemas. Estas tres funciones φ 1 , φ 2 , φ 3 , se definen por, φ1,i(x, w) = x i 2 , φ 2yi (x, w) = w i 2 , φ 3,i (x, w) = X i W i . Además, consideramos el caso φ (x, w) = φ 0(x, w) = 0 que da lugar al reconocido problema de complementariedad horizontal lineal.
En los cuadro 6, 7 y 8 presentamos los resultados obtenidos para el Problema 3, con los Algoritmos PIDP, NE, PGIN y CNIDP para cada una de las funciones < o, < i , < 2, < 3, variando el tamaño de los problemas. En el Cuadro 8, no aparece la fila para p 1 porque los métodos no convergen en este caso.
Observemos que los métodos inexactos tomaron ventaja frente al exacto para n grande (n = 5625). Los Algoritmos NIDP y NE fueron consistentes ya que convergieron a la solución del problema en todos los ensayos, sin embargo la diferencia a favor, en tiempo, para el algoritmo NIDP, fue bastante clara para todos los problemas de tamaño 2500 y 5625. Es importante observar que el Algoritmo NIDP realizó muy pocas iteraciones internas para resolver el sistema (7), en contraste con el gran tamaño del problema.
Para finalizar y con el objetivo de probar nuevamente la robustez del Algoritmo NIDP realizamos 500 ensayos, con cada uno de los cuatro problemas de tamaño 2500 originados por los términos no lineales pi. En el Cuadro 9 registramos el porcentaje de éxitos en cada caso (Éxito), iteraciones promedio (k) y el tiempo promedio (t(s)) para resolver cada uno de los problemas. Los puntos iniciales en cada ensayo fueron generados aleatoriamente de tal forma que sus componentes pertenezcan al intervalo [1, 50].
El hecho que el algoritmo haya convergido en el 100 % de los experimentos habla muy bien de su robustez y aunque la cantidad de iteraciones promedio fue relativamente alta cuando se tomaron las funciones φ1 , φ 2 y φ 3, creemos que el tiempo de ejecución fue bastante aceptable teniendo en cuenta el tamaño del problema a resolver.
5. Comentarios finales
En este trabajo proponemos un algoritmo tipo Newton inexacto global para resolver el problema de complementariedad horizontal. Su principal novedad es la alternativa de usar la proyección de la dirección inexacta de Newton cuando esta no sea de descenso. Además, el algoritmo usa una búsqueda lineal libre de derivadas que asegura un descenso de la función de mérito relacionada a cada problema.
Demostramos que el algoritmo propuesto tiene buenas propiedades de convergencia bajo hipótesis razonables. Presentamos resultados numéricos que contrastan los resultados teóricos presentados en el Capítulo 3 y vislumbran la ventaja de usar métodos inexactos, especialmente para problemas de gran tamaño.
