Mahacine Amrani¹

¹ Ingeniero especializado en procesos industriales, Ecole Mohammadia d'Ingénieurs de Rabat, Marruecos. Participante, numerosos proyectos relacionados con Ingeniería Aplicada a los Procesos Industriales. Profesor, Ingeniería Aplicada y Procesamiento de Señales, Facultad de las Ciencias y Técnicas de Tánger. Curso de Procesos Industriales y Procesamiento de Señales - estudiantes de la maestría en Ingeniería Química, Facultad de las Ciencias y Técnicas de Tánger, Marruecos. Département de Génie Chimique, Faculté des Sciences & Techniques de Tanger. amrani.mahacine@menara.ma

RÉSUMÉ

Ce travail se réfère à la séparation d’un mélange de plusieurs constituants obtenus comme produits de la thermo dégradation du poly(méthacrylate de méthyle) (PMMA).nous désirons purifier le monomère de méthacrylate de méthyle (MMA) obtenu suite à la dégradation thermique à 95% en masse pour atteindre la concentration maximale de 99.5% grâce au procédé de pervaporation. Ce travail a pour objectif d’étudier la théorie de la pervaporation et d’appliquer les principaux critères thermodynamiques pour le choix des membranes en polymères convenables à la séparation du mélange MMA/PRP/ISB. Ces critères thermodynamiques sont basés sur les paramètres d’interaction et des solubilités des monomères dans la membrane. L’avantage de l’utilisation de cette technique de séparation réside principalement dans le fait que cette méthode a une faible consommation énergétique comparée au autres procédés tels : la distillation ou la cristallisation.

Mots-clé: membrane, polymère, solvant, pervaporation, thermodynamique, interaction, solubilité

RESUMEN

Este trabajo describe la separación de una mezcla de varios componentes obtenidos como productos del proceso de termo-degradación del polimetacrilato de metilo (PMMA). Se purificó el monómero de metacrilato de metilo, obtenido por degradación térmica 95% en masa, mediante el proceso de pervaporación hasta obtener una concentración máxima de 99.5%. El objetivo de este trabajo consistió en realizar una revisión conceptual sobre pervaporación y en la aplicación de los principales criterios termodinámicos para la selección de membranas poliméricas para la separación de la mezcla MMA/PRP/ISB. Estos criterios termodinámicos se basan en parámetros de interacción y solubilidad de los monómeros sobre la membrana. La ventaja principal de la utilización de esta técnica de separación reside en el bajo consumo de energía comparado con otros procedimientos, tales como la destilación o la cristalización.

Palabras clave: membrana, polímero, solvente, pervaporación, termodinámica, interacción, solubilidad.

ABSTRACT

This work describes separating a mixture of several components obtained as a product of methyl polymethyl methacrylate (PMMA) thermo-degradation. It was aimed at purifying methyl methacrylate monomer (MMA) obtained by 95% mass thermal degradation to reach 99.5% maximum pervaporation concentration. This work studied the theory of pervaporation and applying the main thermodynamic criteria for choosing suitable polymer membranes for separating the MMA/PRP/ISB mixture. Such thermodynamic criteria were based on monomer interaction with and solubility on the membrane. The advantage of using this separation technique lies mainly in the fact that this method has low energy consumption compared to other processes, such as distillation or crystallisation.

Keywords: membrane, polymer, solvent, pervaporation, thermodynamics, interaction, solubility

Recibido: agosto 24 de 2006 (Received: august 24^th of 2006)
Aceptado: octubre 19 de 2006 (Accepted: october 19^th of 2006)

Introduction

Lors de la séparation des mélanges organiques par pervaporation, le choix de la composition de la membrane approprié s’avère intéressant et complexe. Pour cela, il est intéressant d’établir des critères thermodynamiques qui permettent de choisir, parmi une multitude de polymères, de façon préliminaire quelques compositions de membranes utiles pour des séparations spécifiques. Un des critères de base pour le choix d’une membrane de pervaporation est la valeur d’interaction solvant- polymère χ_AB. Cette valeur se calcule à partir des données des paramètres de solubilité des constituants à séparer et des polymères utilisés en fonction des propriétés physico chimiques.

Dans ce travail, on propose et on étudie un ensemble de critères thermodynamiques utiles pour le choix de la membrane appropriée à la séparation du métacrylate de méthyle (MMA) à partir d’un mélange de MMA, d’isobutinate de méthyle (ISB) et de propionate de méthyle (PRP).

Dans cet article, nous avons utilisé des modèles thermodynamiques et des données bibliographiques pour calculer les paramètres définissant les critères de base dans le choix de la membrane de pervaporation. Tenant compte de l’importance de la séparation du monomère MMA, du choix de la membrane appropriée ainsi que de la complexité du procédé, nous avons procédé à l’élaboration de critères généraux pour faciliter et préparer le travail expérimental. La pervaporation est un procédé de séparation de mélanges liquides à travers une membrane organique. La séparation des dérivés de l’acide acrylique, à savoir le MMA, le ISB et le PRP, produit principalement par dégradation thermique du poly (méthacrylate) de méthyle PMMA. Nous désirons purifier le monomère MMA, obtenu en phase liquide à une concentration en masse approximative de 95% suite à la dégradation thermique.

La pervaporation est une méthode de séparation alternative ne nécessitant pas une grande quantité d’énergie comparée à la distillation. Lors de la séparation à travers les membranes, le processus est généralement sélectif à un ou plusieurs constituants en fonction de la taille, la forme, la charge, l’affinité ou encore la structure chimique de chaque constituant présent dans le mélange de l’alimentation.

La pervaporation est un procédé de fractionnement complexe ou les caractéristiques de séparation peuvent être influencées par la composition du mélange à traiter. Ce procédé est communément utilisé pour enlever un contaminant d’un mélange liquide. Il s’avère très attractif quand il s’agit de contourner la composition azéotropique. Pour améliorer le flux de transfert, il est préférable de choisir une membrane en polymères à l’état viscoélastique car ceci permet d’obtenir une plus grande solubilité des impuretés à séparer. Contrairement à la séparation de mélanges gazeux ou les membranes utilisées sont dans un état cristallin ou semi cristallin (Mulder, 1996). Le mécanisme de dissolution- diffusion est généralement adopté pour expliquer le phénomène de pervaporation, en particulier lors du fractionnement des mélanges d’hydrocarbures ou d’hydrocarbures halogénés.

La pervaporation des mélanges liquides diffère de la pérmeation à constituant unique puisque la solubilité et la diffusivité d’un constituant du mélange peuvent être affectées significativement par la perméation des autres constituants ; comme c’est le cas observé pour la séparation du mélange benzène/hexane/polyéthylène, qui pervapore considérablement plus vite que chacun des constituants seuls (Huang et Lin, 1968). Ces résultats imprévus de perméation sont dus à l’augmentation de la vitesse de diffusion des espèces lentes retenues par la présence des espèces coexistantes. Des conclusions similaires sur l’accouplement des flux de pervaporation ont été rencontrées dans des études récentes (Fels et Huang, 1971 ; Heintz et Stephan, 1994).

Pour la modélisation du phénomène de diffusion d’un mélange liquide à travers une membrane en polymère, nous avons utilisé des relations empiriques linéaires ou exponentielles ou la diffusivité d’un constituant est liée aux concentrations des autres constituants dans le système pénétrant polymère. Cependant de bons résultats ont été obtenus, comparativement aux valeurs expérimentales, et ce par le développement de modèle de volume libre pour la diffusion des mélanges liquides dans les polymères (Fels et Huang, 1971). Une relation linéaire a été développée entre la perméabilité et la concentration dans le cas de mélange liquides quasi-idéaux (Greenlaw et al., 1977; Long, 1965). Une relation exponentielle a été également développée pour relier le coefficient de diffusion à la concentration des espèces pour le mélange eau- éthanol, sans tenir compte des interactions existant entre le pénétrant et la membrane (Mulder et Smolders, 1994). Ce modèle-ci à travers des membranes en latex pour le mélange eau- éthanol a été singulièrement optimisé (Wei et Huang, 1994). Une série de calculs théoriques nous permet d’établir, en ce qui suit, les critères thermodynamiques décisifs pour le choix d’une membrane de pervaporation du mélange que l’on désire traiter. Une fois la membrane choisie, nous avons testé un modèle simple de dissolution- diffusion (Matsura, 1994) pour expliquer le processus de séparation d’un mélange binaire par pervaporation.

Dans ce travail, nous présentons et discutons les valeurs calculées pour :

-les paramètres d’interaction d’une série de polymères avec chacun des constituants que nous nous proposons de séparer.

-les isothermes d’absorption du MMA et des impuretés W dans les systèmes poly (methyl propyl siloxane) PMPM/MMA et PMPS/W.

-les coefficients de diffusion à dilution infinie D₀ pour MMA et W dans le système PMPS/MMA/W.

-les coefficients de diffusion D_i pour les systèmes PMPS/MMA et PMPS/W.

-les coefficients de plasticité γ′ du PMPS en présence de MMA et de W.

-Le taux de mouillage 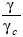pour le PMPS en présence de MMA, ISB et PRP.

Ces cinq paramètres représentent les critères thermodynamiques pour le choix de membranes fonctionnelles en pervaporation pour la séparation de MMA, ISB et PRP.

Rappels théoriques

La pervaporation est un procédé de fractionnement de mélanges homogènes dans lequel, le mélange, initialement liquide traverse une membrane organique selon un processus complexe. Ce dernier implique dans une première étape, la solvatation préférentielle du constituant minoritaire, puis dans une seconde étape la diffusion des espèces dans l’épaisseur de la membrane -qui gonfle par son contenu-, et enfin la vaporisation du liquide à la face aval maintenue sous pression réduite selon deux modes différents : par pompage continu ou par balayage de gaz inerte.

Deux constituants i et j se mélangent spontanément si l’énergie libre du mélange est inférieure à la somme des énergies libres de chaque constituant. Pour séparer un mélange formé spontanément, il est nécessaire de fournir une quantité d’énergie égale ou supérieure à l’énergie libre du mélange ΔG_m. Cette énergie libre, correspondant au travail minimum W_min pour séparer i et j peut être sous forme de chaleur ou de travail mécanique.

L’enthalpie libre du mélange est déterminée à partir des enthalpies libres de chacun des constituants et donc de leur potentiel chimique µ_i donné par l’équation suivante :

En pratique, l’énergie nécessaire pour la séparation des constituants peut dépasser largement la valeur du travail minimum. La cristallisation et la distillation sont accompagnées d’un changement de phase, et donc il faut ajouter la chaleur nécessaire pour la vaporisation ou la solidification. Les procédés à membrane tels l’osmose inverse ou l’électrodialyse ont lieu sans changement de phase, et donc à faible consommation d’énergie. Lors de la pervaporation, la faible pression à l’aval de la membrane favorise le changement de phase du permeat puisque la pression partielle d’un constituant dans la membrane est supérieure à la pression du vide à l’aval de la membrane.

Mécanisme de dissolution- diffusion d’un mélange binaire

Le gradient de potentiel chimique à travers la membrane est considéré comme une force motrice pour le transfert en masse dans le procédé de pervaporation. Pour chaque constituant, ce gradient peut s’écrire sous la forme :

ou a_im est l’activité du constituant i dans la membrane et V_i le volume molaire du constituant i. ∇p est le gradient de pression entre la face amont et aval de la membrane et T la température du système. On considère que la pression de l’alimentation reste constante lorsque les constituants traversent la membrane de largeur l comme le montre la Figure 1.

La première loi de Fick nous permet d’écrire l’équation de transport selon la forme :

L’équilibre thermodynamique qui s’établit entre la face amont et aval de la membrane peut être représenté par les équations suivantes :

Les indices 2 et 3 correspondent respectivement à la face en contact avec la dissolution et celle en contact avec la pérméation. En outre, nous savons que

ou µ₀ est le potentiel chimique standard d’un constituant pur. L’équilibre thermodynamique d’un constituant i entre les deux faces de la membrane s’écrit alors :

En considérant que la pression de dissolution à l’amont P₂ décroît à l’intérieur de la membrane jusqu’à l’aval de celle-ci, les équations (8) et (9) peuvent s’écrire sous la forme :

L’activité étant égale au produit du coefficient d’activité par la concentration, nous avons :

Si l’on définit le coefficient de répartition K, comme le rapport des coefficients d’activité pour chaque constituant et , les équations (12) et (13) deviennent alors:

L’équation (4) devient alors :

Ce qui nous permet de calculer le flux de transfert de chaque constituant i à travers la membrane.

Absorption de solvant dans un réseau de polymères

Les isothermes d’absorption, en particulier dans le cas de composés organiques sur des matériaux élastomères, peuvent être décrites moyennant l’expression suivante (Favre et al., 1993):

ou les indices s et p se référent respectivement au solvant et au polymère, V étant le volume molaire et φ la fraction de volume dans le système solvant- polymère, a_s est l’activité du solvant dans la membrane et χ le paramètre d’interaction solvant- polymère. La valeur de χ peut être obtenue par l'équation :

ou χ_s est le terme de contribution entropique, χ_h terme de contribution enthalpique, δ_s et δ_p étant les paramètres de solubilité respectifs du solvant et du polymère.

Diffusion du solvant dans le réseau de polymères

Différentes expression permettent de relier la diffusivité du solvant à la concentration de celui-ci dans le polymère. Elles ont été dérivées de la théorie du volume libre. Dans ce qui suit, une relation exponentielle simple permet d’observer l’interdépendance du coefficient de diffusion et de la fraction volumique du solvant dans la membrane φ_s. Cette relation, très usitée pour sa simplicité, décrit de façon adéquate la relation entre le coefficient de diffusion et la concentration (Favre et al., 1994):

ou D₀ est le coefficient de diffusion à dissolution infinie et γ′ le coefficient de plasticité relatif à l’augmentation du volume libre dans le réseau de polymères après absorption du solvant. Cette expression a été utilisée pour calculer le coefficient de plasticité à partir de données de D_0i et des valeurs de D calculées à l’aide de l’équation (23) (Favre et al., 1994).

Mouillage de la membrane organique solide par les solutions

Le rapport des tensions superficielles 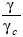permet de prévoir le taux de mouillage d’un matériau solide, tel un film membranaire de tension superficielle γ_c, par un liquide de tension superficielle γ. La membrane n’est pas mouillée si 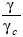≥1. L’angle de contact pour le mouillage se forme sous l’effet des trois tensions inter faciales entre le solide, le liquide et le gaz, selon l’équation de Young :

Les indices s,l,v se référent respectivement à l’état solide, liquide et vapeur. Pour déterminer expérimentalement la tension superficielle critique, on mesure les angles de contact entre le film organique et divers liquides à température constante. γ_c correspond à la tension superficielle du liquide pour une valeur de cosυ=1.γ_c est donc donnée par l’équation

Procédure de calcul

Le choix de la membrane adéquate pour notre problème de séparation a été dicté par le calcul du paramètre d’interaction χ à l’aide de l’équation (18). Une fois la membrane choisie, nous avons calculé le taux de mouillage 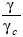, les coefficients de diffusion à dilution infinie D_0i (équation 22), les coefficients de diffusion D_i (équation 23) les coefficients de plasticité γ′ (équation 25) pour le système choisi. Nous avons pu, aussi appliquer un simple modèle de dissolution-diffusion pour obtenir les valeurs de la perméabilité P_i, les flux de pervaporation J_i et les facteurs de séparation SF_i^j. Ces résultats sont présentés et discutés dans ce qui suit.

Résultats et discussions

Calcul des paramètres de solubilité

L’utilisation des paramètres de solubilité δ_s et δ_p du solvant et du polymère respectivement reste un critère thermodynamique de choix pour sélectionner le solvant adéquat au polymère considéré. Ces paramètres sont liés également à la polarité du matériau. De manière générale, le bon solvant correspond à celui dont le paramètre de solubilité se trouve dans l’intervalle : δ_p-1.1≤δ_s≤δ_p+1.1. Le Tableau 1 présente les différents paramètres de solubilité et classés selon leur polarité croissante (Barton, 1990).

Calcul des paramètres d’interaction χ

En tenant compte des critères thermodynamiques de miscibilité et de compatibilité, le choix d’une membrane efficace pour la séparation d’un mélange liquide peut se faire en utilisant les paramètres d’interaction solvant – polymère χ. Ce paramètre s’annule lorsque la dissolution est totale. Un bon solvant de pervaporation correspond à des valeurs de χ≤0.8 (Favre, et al., 1993). Ce qui est le cas du PDMS et divers solvants considérés. La valeur de χ est déterminée en utilisant l’équation semi-empirique (18) pour différents systèmes, et particulièrement pour le système PMPS / MMA- ISB- PRP décrit pat le Tableau 2.

Les valeurs de δ du Tableau 1 ont été utilisées dans l’équation (18) pour calculer le terme enthalpique χ_h; le terme entropique a été pris égal à 0.35, valeur acceptable pour ce type de systèmes en pervaporation. Dans la Tableau 2, nous avons marqué en gras les polymères montrant une grande interaction avec les impuretés ISP et PRP.

Tracé des isothermes d'absorption pour un système solvant- polymère

Nous avons procédé à l’étude du comportement des liquides à séparer sur une membrane en PMPS en accord avec le critère thermodynamique du paramètre d’interaction χ. Pour déterminer les isothermes d’absorption des systèmes PMPS / MMA et PMPS/W ou W correspond principalement aux impuretés ISB et PRP nous avons utilisé l’équation (17). Pour différentes compositions φ_i, nous avons calculé les activités correspondante du MMA et des impuretés W. on remarque que la valeur de l’activité a_MMA atteint la valeur de 1 lorsque la composition du mélange est φ_MMA=0.612 et l’activité des impuretés a_W=1 lorsque φ_W=0.797 (Figure 2 et 3)

3.5.Corrélation entre le coefficient de diffusion à dilution infinie et le volume molaire du pénétrant

Le coefficient de diffusion à dilution infinie D_0i est un paramètre primordial pour quantifier la diffusion d’un pénétrant à travers une membrane donnée. Une relation linéaire entre h D_0i et le volume du pénétrant V_i pour différents systèmes polymère/ pénétrant est usuellement utilisée en accord avec l’expression (22) (Favre, et al., 1994):

ou A et B sont des constantes obtenues graphiquement.

Diverses valeurs de D_0i existent pour le système PDMS et diffèrents pénétrants, et dont quelques uns présentent une certaine similitude en forme et en taille avec les substances que nous désirons séparer (Favre, et al., 1994). Sur la figure 5, un ajustement linéaire ainsi que des interpolations ont été effectués pour les données de D_0i afin d’obtenir des valeurs correspondant au PRP, ISB et le MMA.

Calcul des coefficients de diffusion et de plasticité des systèmes PMPS/MMA et PMPS/W

Plusieurs relations mathématiques ont été proposées pour expliquer la variation du coefficient de diffusion en fonction de la concentration :

Le terme d h a_i / d h φ_l est obtenu en différenciant l’équation (17) par rapport à h φ_s dans l’équation (24), lorsque le système tend vers l’idéalité, c’est à dire, lorsque la fraction du volume du pénétrant φ_l tend vers 0, le rapport [d h a_i / d h φ_l] tend vers 1.

La méthode graphique permet de déterminer la valeur de d h a_i / d h φ_l d’une autre façon en calculant les pentes de la courbe de h a_i en fonction de h φ_i comme le présente la Figure 4.

Nous avons calculé des deux manières citées la valeur du rapport d ln a_i / d ln φ_l. Cette valeur, injectée dans l’équation (23) afin de calculer le coefficient de diffusion D_ij, permet de calculer ensuite le coefficient de plasticité γ′ et donc obtenir le meilleure corrélation entre le coefficient de diffusion et la concentration du pénétrant. La linéarisation de l’équation (19) nous permet d’écrire :

ou γ′ est le coefficient de plasticité caractéristique à chaque système pénétrant polymère. La valeur de γ′ est un critère important pour le choix de la membrane convenable à la séparation des constituants. Les courbes de h D_i en fonction de φ_i ont été tracées pour les systèmes PMPS/MMA et PMPS/W dans le but de déterminer les valeurs de γ′. Les Figures 6 et 7 décrivent le comportement du coefficient de diffusion en fonction de la concentration. Comme l’on peut l’observer sur la figure 5, au fur et à mesure que la concentration de MMA dans le système augmente, la valeur de son coefficient de diffusion diminue sensiblement. le même comportement est observé pour les impuretés W, à la seule différence que les variations de D_W en fonction de φ_W sont plus faibles, ce qui favorise la séparation des constituants du mélange.

Critères de mouillage de la membrane en contact avec les constituants à séparer

En accord avec la théorie de l’angle de contact, la membrane de pervaporation en polymère solide n’est pas mouillée lorsque le rapport des tensions superficielles 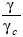est supérieur à l’unité. Les valeurs des tensions superficielles critiques γ_c pour les membranes hydrophobes et hydrophiles, ainsi que les tensions superficielles des constituants à séparer sont données par des tables standard (Rodríguez et al., 2003). La figure 8 décrit la variation du taux de mouillage 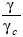en fonction de la température en Kelvin. On utilise l’équation (26) pour calculer γ et on considère γ_c du PDMS constante et égale à celle proposée par le Tableau 3.

A et B sont des constante caractéristiques à chaque constituant à séparer et T_r la température réduite correspondante. Ce critère nous permet de choisir une température opératoire optimale pour séparer les constituants du mélange. Pour cela, si nous désirons retenir le MMA, il serait plus judicieux de travailler à des températures pour lesquelles le ISB et le PRP mouillent plus facilement le PDMS ou le PMPS que le MMA. Cette température doit être comprise entre 273K (0°C) et 287K (14°C). Pour des températures supérieures à 14°C, le MMA mouille la membrane de PDMS à une moindre proportion que le ISB ou le PRP. Ce qui permettra que ceux-ci s’absorbent préférentiellement et traversent la membrane plus facilement.

Conclusions

Dans ce travail nous nous sommes intéressé à quelques aspects physico-chimiques du procédé de pervaporation. Nous avons établi et appliqué divers critères thermodynamiques pour le choix d’une membrane convenable pour la séparation du mélange à séparer. L’utilisation des paramètres d’interaction polymère- pénétrant χ nous permet de sélectionner la membrane à utiliser. Deux membranes se sont avérées convenables pour notre cas, à savoir la membrane en PMPS et celle en PMOS en accord avec les valeurs de χ calculées. Dans le système d’absorption PMPS/MMA, la valeur unitaire de l’activité est atteinte pour une concentration en MMA de φ_MMA=0.612, alors que pour le système PMPS/W, la valeur a_W=1 est atteinte pour une concentration φ_W=0.797. En accord avec le modèle utilisé, le coefficient de diffusion à dilution infinie D_0i diminue de façon semi-logarithmique lorsque le volume molaire des pénétrants MMA, ISB et PRP augmente. Lorsque la concentration de certains pénétrants augmente, leurs coefficient de diffusion respectifs diminue de façon semi-logarithmique. Néanmoins, pour les faibles concentrations, les impuretés diffusent plus rapidement que le MMA. Ce qui permet leur élimination. Lorsqu’on applique le critère de mouillage 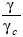nous pouvons affirmer qu’à des températures de 287 K, le MMA ne mouille pas la membrane en PDMS, contrairement aux impuretés. Ce qui facilite sensiblement la séparation des impuretés.

Références

Mulder, M.V.H., Basic Principles of Memnrane Technology, 2^nd Edition, Kluwer Academic Publishers, 1996, pp. 584.        [ Links ]

Huang, R.Y. and Lin, V.J.C., Separation of liquid mixtures by using polymer membranes. I. Permeation of binary organic liquid mixtures through polyethylene., J.Appl. Polym.Sci, 12, 1968, pp. 2615-2631.        [ Links ]

Fels, M. and Huang., R.Y.M., Theoretical interpretation of the effect of mixture composition on separation of liquids in polymers., J. Macromol. Sci. Phys., B5, 1, 1971, pp. 89-110.        [ Links ]

Heintz, A. and Stephan, W.J., A generalized solution—diffusion model of the pervaporation process through composite membranes Part I. Prediction of mixture solubilities in the dense active layer using the UNIQUAC model, J. Membrane Sci., 89, 1994, pp. 143-151.        [ Links ]

Greenlaw, F.W., Shelden, R.A. and Thompson, E.V., Dependence of diffusive permeation rates on upstream and downstream pressures : II. Two component permeant., J. Membrane Sci., 2, 1977, pp. 333-348.        [ Links ]

Long, R.B., Liquid Permeation through Plastic Films., Ind. Eng. Chem. Fundam.,4, 1965, pp. 445 – 451.        [ Links ]

Mulder, M.H.V. and Smolders, C.A, On the mechanism of separation of ethanol/water mixtures by pervaporation I. Calculations of concentration profiles, J. Membrane Sci., 17, 1994, pp. 289-307.        [ Links ]

Wei, Y. and Huang, R.Y.M., Selective sorption of latex membranes with ethanol-water mixtures., Sep. Sc. Technol., 29, 1994, pp. 301-314.        [ Links ]

Matsura, T., Synthetic membranes and membranes processes., 467 pp,CRC Press Inc, Boca Raton, 1994.         [ Links ]

Favre, E., Nguyen, Q.T, Schaetzel, P., Clement, R. and Neel, J., Sorption of organic solvents into dense silicon membranes, Part.I, Validity and limitations of Flory-Huggins and related theories., J. Chem. Soc. Faraday Trans., 89, 1993, pp. 4339-4346.        [ Links ]

Favre, E., Shaetzel, P., Nguygen, Q.T., Clément, R. and Néel, J., Sorption, diffusion and vapor permeation of various penetrants through dense poly(dimethylsiloxane) membranes: a transport analysis., J. Membrane Sci., 92, 1994, pp. 169-184.         [ Links ]

Barton, A.F.M, Handbook of polymer-liquid interaction parameter and solubility parameters., Murdoch University, CRC Press, Australie, 1990, pp. 768.        [ Links ]

Rodriguez, F., Cohen, C. and Archer, L., Principles of polymer systems., Taylor & Francis Books, 5th Edition, 2003, pp. 774.        [ Links ]