ARTÍCULO ORIGINAL

Codificador RS(n,k) basado en LFCS: caso de estudio RS(7,3)

RS(n,k) Encoder based on LFCS

Cecilia Sandoval-Ruiz*

Grupo de investigación en Tecnologías Digitales Aplicadas a Telecomunica–ciones. Universidad Nacional Experimental Politécnica de la Fuerza Armada Bolivariana (UNEFA), A.A. 2103. Maracay, Venezuela.

^*Autor de correspondencia: teléfono: + 58 + 0414 + 9447293, correo electrónico: csandoval1@uc.edu.ve (C. Sandoval)

(Recibido el 01 de septiembre de 2011. Aceptado el 28 de agosto de 2012)

Resumen

El presente artículo presenta el diseño de un codificador Reed Solomon basado en un circuito concurrente, LFCS - Linear Feedback Concurrent Structure- que permite la generación de los símbolos de redundancia del código de forma paralela, siempre que se le suministren los k símbolos de información a codificar de forma simultánea, el codificador ofrece a su salida los símbolos de redundancia correspondientes. Para lograr este desarrollo se generalizó el modelo matemáticos para la descripción del comportamiento del codificador, se realizó la configuración en lenguaje descriptor de hardware VHDL de un codificador Reed Solomon, tomando como caso de estudio el RS(7,3), se simuló el diseño propuesto validando así su funcionamiento, para finalmente realizar la comparación de la implementación del codificador entre la versión secuencial y la versión basada en LFCS, obteniendo una reducción de componentes hardware y optimizando la velocidad de respuesta y consumo de potencia. Concluyendo, que el diseño del codificador propuesto valida el modelo concurrente generalizado a partir de la correspondencia con la arquitectura del LFCS.

Palabras Clave: LFCS, codifi cador reed solomon, diseño concurrente

Abstract

This article presents the design of a Reed Solomon encoder circuit based on a concurrent LFCS -Linear Structure Concurrent Feedback- allowing the generation of code redundancy symbols in parallel, provided that you supply the k information symbols to encode simultaneously, the encoder provides at its output corresponding redundancy symbols. To achieve this development was generalized mathematical model describing the behavior of the encoder, the configuration was done in VHDL hardware description language of a Reed Solomon encoder, taking as case study the RS (7.3), the design was simulated validating the proposed operation, and finally the comparison of the encoder implementation between the sequential version and the version based on LFCS, obtaining a reduction of hardware components and optimizing the speed of response and power consumption. In conclusion, the proposed encoder design validates the concurrent model generalized from the correspondence with the architecture of LFCS.

Keywords: LFCS, reed solomon encoder, concurrent design

Introducción

El codificador Reed Solomon encuentra su vigencia tecnológica de acuerdo a las prestaciones y grado de complejidad del decodificador, característica que lo hace competitivo entre las alternativas de codificación de canal, lo que motiva una investigación acerca de la optimización del modelo que permita describir este codificador a nivel de hardware.

En investigaciones previas, se han desarrollado los codificadores Reed Solomon en VHDL (del inglés, Very High Speed Integrated Circuit Hardware Description Language) usando para ello, algoritmos secuenciales [1], estos codificadores demandan una gran capacidad de cómputo en su implementación, a fin de obtener una alta velocidad de procesamiento, estando su velocidad de respuesta en la salida del codificador siempre limitada por el hardware sobre el cual se implementa el circuito. Los desarrollos en tecnología para implementación de hardware por su parte representan una alternativa de solución para cubrir la demanda en cuanto a capacidad de cómputo y velocidad, siendo cada vez más evidente la nece–sidad de optimización de los modelos de acuerdo a la filosofía de diseño sobre tecnología de hardware reconfigurable, que se maneja actualmente. Es por ello que en esta investigación se propone la paralelización del codificador Reed Solomon, usando un caso de estudio para la comprobación del funcionamiento basado en el desarrollo de ecuaciones que describan el modelo matemático concurrente del codificador RS, el método empleado para la obtención de estas ecuaciones ha sido el análisis del proceso secuencial, descripción generalizada de la composición de vectores y correspondencia con la paralelización del circuito LFSR (del inglés, Linear Feedback Shift Register).

Los codificadores Reed Solomon RS(n,k), donde n, es el número de símbolos del código y k, número de símbolos de datos, son ampliamente empleados en sistemas de comunicaciones, una de sus aplicaciones consiste en el diseño de los Códigos Turbo Producto Reed Solomon TC-RS [2], al momento de implementar la matriz de codificación, el codificador cruzado depende de los símbolos de redundancia generados por el primer codificador, esto demanda la implementación de un codificador rápido, preferiblemente paralelo, para así tener los datos de entrada del segundo codificador en un solo pulso de reloj. En tal sentido; en este trabajo se presenta la propuesta de un codificador paralelo, basado en la arquitectura de un LFSR concurrente, el cual se ha denominado Linear Feedback Concurrent Structure - LFCS.

Es importante señalar que el estudio de la arquitectura del codificador RS en la presente investigación ha sido orientado hacia una solución de hardware, por lo cual su descripción debe estar dada para un dispositivo de hardware configurable y de tecnología actualizada para el modelo que acá se plantea como solución, en este aspecto se selecciona la tecnología FPGA (del inglés, Field Programmable Gate Arrays).

Fundamentos de los Códigos Reed Solomon

Al momento de seleccionar el objeto de estudio para la presente investigación se han considerado factores de relevancia y vigencia tecnológica de los códigos Reed Solomon. Teniendo presente que si bien existen actualmente alternativas de codificación con buenas prestaciones, es el código RS uno de los que resulta más competitivo desde el punto de vista de la complejidad del decodificador [2]. Esto en contraste con los Turbo Códigos, los cuales presentan ventajas en el dominio de transmisión de datos, pero se ven limitados para transmisión de voz y video, por la demandas de cómputo en las etapas del intercalador/des-intercalador en tiempo real.

Esta investigación se inicia a partir de una detallada revisión sobre los desarrollos de los códigos RS, encontrando un amplio campo de aplicación de dichos códigos en los sistemas de comunicaciones, tales como; Digital Video Broadcast (DVB). Digital Satellite Broadcast (ETS 300- 421satellite, ETS 300-429 cable), Intelsat Earth Stations (IESS-308), Space Telemetry Systems (CCSDS,. ADSL Transceivers (ITU G.992.1), Wireless Broadband Systems (IEEE 802.16), 2.5G, 10G and 40G Optical Networks (ITUT G.795). Es por tal motivo, considerando las aplicaciones y las alternativas de concatenación de códigos, como es el caso de códigos Turbo Productos basados en codificadores Reed Solomon, que se plantea la mejora en el desempeño del codificador, encontramos fundamental optimizar el diseño de los componentes constitutivos del código, a fin de obtener una mayor eficiencia, en cuanto a capacidad de cómputo en los codifica–dores y velocidad de respuesta, para así disponer de códigos compuestos óptimos, de allí que se decidió el estudio y optimización del codificador RS(n,k), componente básico de estos esquemas de codificación híbridos, lo que justifica el desarrollo de un codificador RS paralelo.

Modalidades de Implementación del Codificador RS basado en VHDL

A continuación se presenta una comparación entre la implementación del Codificador Reed Solomon de forma secuencial y de forma paralela, basadas en los conceptos de procesos secuenciales y asignaciones concurrentes manejadas en lenguaje VHDL, para diseño de hardware.

El codificador Reed Solomon puede ser descrito en VHDL a través de un proceso secuencial, el cual consiste en un conjunto de instrucciones ordenadas bajo una secuencia lógica de ejecución, donde una instrucción dependa del resultado de la instrucción anterior, existe un elemento temporal a considerar que controla el orden de ejecución de cada instrucción. La instrucción de sintaxis process se emplea para describir la parte secuencial de un circuito. A efectos de la simulación, solo se ejecutará el process cuando se detecte variación de las señales declaradas en la lista de sensibilidad del proceso, en el proceso las sentencias seguirán una secuencia que depende de la ocurrencia de un cambio en la señal para la cual el proceso es sensible, motivo por el cual se debe declarar una lista de señales sensibles asociadas al proceso, es decir, una señal de reloj para la sincronización de las instrucciones, en el caso del codificador RS se requieren n pulsos de reloj, siendo n el número de símbolos del código.

Gracias al diseño orientado a hardware, el codificador puede ser descrito a través de asignaciones concurrentes, este tipo de asignaciones pueden definirse como operaciones sobre señales que coinciden en el tiempo, dicho de otra forma, la salida de la asignación obtendrá su valor en función de los valores de las n señales de entrada. Para comprender mejor el concepto podemos concentrar la atención en un circuito con múltiples etapas de hardware, dispositivos en cascada, los cuales generan una salida en función de sus entradas, algunos de estos componentes pueden tener señal reloj, sin embargo; el orden de las señales se maneja a través de las entradas, permitiendo que el vector de salida R(x) del codificador RS, se genere en un solo pulso de reloj, obteniendo los símbolos de datos y los símbolos de redundancia de forma simultánea, de esta manera se presenta una solución al codificador RS con salida paralela, lo que lo hace un código más eficiente y competitivo.

Codificador Reed Solomon Paralelo

Previas investigaciones han desarrollado paralelización de etapas de los codificadores Reed Solomon paralelos [3], se han presentado modificaciones al algoritmo de Euclides para paralelizar etapas del decodificador [4], todo esto promueve el diseño de codificadores RS paralelos, en vista que la paralelización es un objetivo para el procesamiento de los datos para corrección de errores, en el mismo orden de ideas, se han desarrollado ecuaciones de paralelización de las funciones del codificador, planteando la codificación a través de unidades de procesamiento paralelas basadas en multi-núcleos [5].

Arquitectura del Generador de Redundancia en el codificador RS

En el estudio del codificador Reed Solomon [1], podemos detectar una arquitectura característica del generador de código, ésta es denominada LFSR - Linear Feedback Shift Register, corresponde a un circuito secuencial que permite la generación de los símbolos de redundancia, cuyo número de etapas estará dado por la diferencia entre los parámetros n,k. A su vez, esta arquitectura está compuesta de elementos base como lo son los multiplicadores, los n,k elementos de memoria y las compuertas xor para los b bits por símbolos. Al momento de describir la arquitectura podemos definir los parámetros de escalabilidad del codificador de forma genérica, con lo cual la longitud del LFSR será ajustable, en función de los parámetros n y k del codificador, de igual manera se debe ajustar el polinomio generados del código, lo cual incide sobre los coeficientes que serán establecidos en la descripción VHDL, los cuales se pueden identificar de forma genérica. Por otra parte, se puede ajustar el tamaño del símbolo, a través del parámetro b, asociado este al tamaño del bus y de la capacidad de los multiplicadores, todos estos parámetros serán ajustables en el diseño, destacando que de ellos dependen los coeficientes del polinomio irreducible del campo P(X) para el circuito del multiplicador y los coeficientes del polinomio generador del código G(X) para el circuito LFSR del codificador. Al momento de realizar la descripción en VHDL requerimos manejar la arquitectura del codificador [1], la cual corresponde con la figura 1.

El generador de símbolos de redundancia del codificador recibe el primer símbolo de los datos de entrada d(i), éste pasa a la salida a través del componente selector del símbolo de salida (Mux de salida), a la vez es operado con el dato almacenado en el registro menos significativo r(0) a través de la xor de entrada, el resultado es ingresado a través de un siguiente multiplexor (Mux de entrada) al circuito LFSR y se realiza la operación de multiplicación en algebra de campos finitos de Galois con cada uno de los coeficientes del polinomio generador G(x), el resultado del producto se operan a través de una xor de b bits, ancho del símbolo, con la salida del registro precedente, al recibir la señal de reloj, el dato es almacenado en el registro a la salida de la xor, el proceso se realiza para los k símbolos, los resultados dependen de la secuencia de símbolos de entrada, posteriormente el multiplexor de salida selecciona el símbolo del r(0) durante (n-k) pulsos de reloj, los cuales corresponden a los símbolos de redundancia.

Al realizar el análisis de la secuencia, se obtienen las ecuaciones en el tiempo de cada símbolo de redundancia, este estudio genérico se empleó para la generación del modelo matemático adaptado a la descripción en lenguaje VHDL.

Metodología

El primer paso que se realizó fue estructurar el circuito del LFSR secuencial, seguidamente se generó cada vector de símbolos de salida del LFSR, a través de n pulsos de reloj, como se presenta en la figura 2, con un polinomio generador G(x)=5,7,7,4 y con un vector de entrada de datos D(x)=1,3,7.

Aplicación del LFCS para el generador de redundancia

A partir de la observación del comportamiento del generador de símbolos de redundancia del codificador Reed Solomon, se reconoció una arquitectura coincidente con el circuito de reducción modular, donde existe una correspondencia entre los coeficientes del polinomio generador que define el código Reed Solomon y los coeficientes del polinomio irreducible que define el campo de Galois, motivo por el cual se consideró evaluar la extensión del modelo concurrente del LFCS desarrollado en la paralelización del multiplicador en campos de Galois [6] al circuito generador del código.

Así la relación lógica-matemática, para cada uno de los elementos generados por el componente LFSR, es presentada en la tabla 1.

Donde r_t es un vector de i símbolos de b bits cada uno, para generar cada término se presenta una relación entre los vectores en el instante t y t+1, la operación corresponde a la operación producto en el campo GF (de sus siglas en inglés, Galois Finite), entre los símbolos de r_t y los coeficientes del polinomio generador G(x) y el componente corresponde a la operación suma en el campo GF, la cual coincide con la XOR lógica. En t = 0 se inicializa el vector R(x), para cada pulso de reloj se obtendrá un nuevo vector que es función del vector en t = t-1 y del correspondiente símbolo del vector a codificar que se ha denominado, datos de entrada, donde el cálculo de cada elemento está dado por el producto entre los coeficientes de cada elemento g_i y el símbolo que se realimenta, es decir el símbolo menos significativo del vector R(x).

Desarrollo del Modelo Concurrente del Codificador RS(n,k)

Para generar cada símbolo, correspondiente a aplicar el circuito LFSR sobre un polinomio de datos de entrada D(x), cuyos coeficientes serán representados por los símbolos de datos, el cual depende del instante de tiempo y la posición del elemento en el polinomio, G(x) el polinomio generador del código, el cual tendrá representados sus elementos por el coeficiente g_i, el cual será fijo en el tiempo y su valor depende de la posición, de donde se obtuvo la ecuación 1.

Donde r_t(i) corresponde al símbolo i del vector R(x) en un instante de tiempo t, r_t-1(i) corresponde al símbolo almacenado en el registro un instante de tiempo anterior, d(i) corresponde al símbolo en la entrada de datos y d(i) el coeficiente del polinomio generador que es fijo en la arquitectura.

Seguidamente, se definió la ecuación general del vector R(x) para cada instante de tiempo, el cual corresponde a la concatenación de los términos obtenidos para cada elemento i en la ecuación 1, donde se empleará el símbolo '&' para indicar la operación de concatenación a fin de coincidir con la descripción en VHDL, de donde se obtiene la ecuación 2.

Siendo r_t el vector generado en un tiempo t de aplicar el circuito de generación de símbolos de redundancia. De esta manera, se tomó el modelo del circuito de estructura concurrente de realimentación lineal para la generación de los símbolos de redundancia del codificador Reed Solomon, partiendo del LFSR que forma parte de la arquitectura del codificador RS, cuya longitud está dada por los n-k registros, de b bits cada uno, se obtiene el modelo paralelizado, en el cual cada palabra corresponde a un elemento del campo finito GF(2^m), de esta manera, se procedió a la generalización de la ecuación del LFCS, esta vez aplicable a registros de capacidad de b bits, al desarrollar la ecuación 2, se obtiene la expresión presentada en la ecuación 3, que corresponde a la aplicación del modelo concurrente del LFSR para la descripción del codificador paralelo.

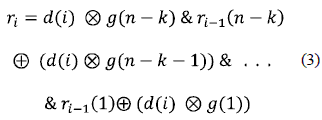
Para la implementación en VHDL se ha expresado el factor de la multiplicación en algebra finita de Galois, a través de la salida del multiplicador como operando del LFSR concurrente, siendo éste un componente implementado en VHDL para la obtención del producto en el campo finito, por lo cual el resultado se debe expresar como un único término, para lo cual la ecuación del modelo se reescribe identificando al producto en el campo GF como m_t,i tal como se observa en la ecuación 4.

Esta ecuación permite generar las salidas del LFSR en un instante t, la cual dependen de los valores anteriores, la generación de los n-k vectores permite obtener los símbolos de redundancia del código de manera concurrente, sin requerir una secuencia sincronizada por señal de reloj, siendo el vector concatenado el resultado de los símbolos de datos y los símbolos de redundancia.

En la tabla 2 podemos observar la descripción VHDL de este codificador seleccionado.

En la figura 3, se puede observar la respuesta concurrente, es decir; la salida paralela. Donde el polinomio generador del código corresponde a G(x) = 5,7,7,4, los símbolos de entrada de datos (e1,e2,e3) están dados por el vector D(x) = 1,3,7, los símbolos de redundancia generados (s4,s5,s6,s7) se presentan a través del vector R(x) = 0,1,1,5, de manera de obtener finalmente en la salida del codificador RS(7,3) paralelo, los símbolos de salida de datos (s1 a s7), dados por el vector S(x) = 1,3,7,0,1,1,5, donde se valida el comportamiento del codificador con el modelo paralelo desarrollado.

Uno de los análisis que resultó de interés consistió en el consumo de recursos de hardware entre la implementación secuencial, que comprende la descripción VHDL [1] y la implementación paralela, encontrando los reportes sintetizados en la tabla 3. Donde se puede observar, una importante mejora tanto en tiempo de respuesta, como en consumo de recursos de hardware en el diseño paralelo que se ha desarrollado bajo el modelo del LFCS generado a través de esta investigación.

Los slice corresponden a los bloques lógicos funcionales que constituyen la arquitectura del FPGA, los arreglos de estas unidades funcionales permiten la implementación en hardware del diseño, para el codificador RS secuencial se requieren 8 slices del dispositivo XC5vlx50T- 3FF1136, mientras que en el diseño paralelo se requieren 11 slice, tal como es de esperarse debido a que las funciones lógicas deben implementarse de forma paralela y no se comparten recursos de hardware como en el caso secuencial, sin embargo, la utilización de flipflops (Slice FF) en la implementación secuencial demanda 12, correspondientes a los n-k registros de b bits cada uno, en tanto que el codificador RS paralelo no requiere de elementos de memoria, las tablas de búsqueda LUTs4 para el caso secuencial se requieren 20 en contraste con el modelo paralelo que solo requiere 13, de manera que se evidencia un ahorro en componentes de hardware considerable, aun teniendo en cuenta que el objetivo de este diseño es la aumentar la velocidad de codificación, de donde se observa que el codificador secuencial requiere una señal de reloj, n pulsos de reloj para completar una codificación, en este caso 7*Delay Máx que se traduce en 85,645ns, esto versus el procesamiento paralelo que no requiere señal de reloj y tiene un retardo máximo de 10,621 ns, con respecto a los cambios en las entradas del codificador RS.

Es oportuno señalar que uno de los aspectos críticos corresponde a los retardos del circuito combinacional, debido a la profundidad lógica del diseño paralelo, sin embargo, esto ha sido solventado directamente por la herramienta de desarrollo ISE11, que cuenta con la capacidad de optimización de la distribución a través del proceso de síntesis, al tratarse el diseño a nivel de la tecnología del dispositivo, basada en LUTs en lugar de compuertas, lo que simplifica el número de etapas definido como complejidad lógica del circuito final.

En la figura 4, se reportan los resultados del consumo de potencia suministrada en el reporte de la herramienta de desarrollo ISE 11.

Se puede observar una optimización en el consumo de potencia asociado al diseño sobre el modelo paralelo, ya que la potencia del circuito lógico es de 0,05mW para ambos diseños, la potencia asociada a las señales es de 0,33 mW en el diseño paralelo vs. 0,13 mW en el diseño secuencial, pero la relación de la potencia consumida por el reloj (clk) corresponde a 0,48 mW en el diseño secuencial, en tanto que para el diseño paralelo no aplica, de este modo se tiene un ahorro de potencia dinámica de un 42,42%, vale destacar que el consumo de potencia dinámica ha sido calculado sin considerar la potencia disipada en los pines de entrada y salida, esto debido a que el diseño es un componente del sistema de comunicación donde las IO (entradas-salidas) no son implementadas en los pines del dispositivo, en ese caso encontramos que el número de entradas / salidas es mayor para el diseño paralelo.

Conclusiones

Se empleó la teoría de correspondencia entre la arquitectura de los LFSR del multiplicador GF y del generador de redundancia para realizar la interpretación secuencial de la arquitectura y generar las ecuaciones que describen el modelo concurrente en VHDL, lo que aporta a la comunidad científica un modelo matemático- lógico para la configuración del codificador Reed Solomon paralelo basado en el concepto de asignaciones concurrentes para descripción de hardware y se logró su validación a través de simulación para el caso de estudio considerado.

Con los resultados obtenidos se realizó el análisis de eficiencia con respecto a investigaciones previas de modelos secuenciales del RS(7,3) [1], siendo el modelo paralelo apropiado para su implementación sobre hardware, usando VHDL, tecnología que ofrece soporte a tales niveles de paralelización, esto ampliamente justificado en la tendencia hacia el desarrollo de decodificadores paralelos [3-4]. El trabajo desarrollado aporta un modelo general que puede ser aplicado para la implementación de cualquier codificador RS(n,k), con valores del polinomio generador G(x) ajustables de acuerdo al diseño.

Referencias

1. C. Sandoval, A. Fedón. ''Codificador y decodificador digital Reed-Solomon programados para hardware reconfigurable''. Revista Ingeniería y Universidad. Vol. 11. 2007. pp. 17-31.         [ Links ]

2. C. Hsie, B. Shung, L. Chen. ''A Reed-Solomon Product-Code (RS-PC) Decoder Chip for DVD Applications''. IEEE Journal of Solid-State Circuits. Vol. 36. N°. 2. pp. 229-238. 2001. Available in: http://www.si2lab.org/publications/jnl/hcchang_jssc_01.pdf. Consultada el 23 de enero de 2011.         [ Links ]

3. C. Chang, A. Hyo, L. ''High-Throughput Low- Complexity Four-Parallel Reed-Solomon Decoder Architecture for High-Rate WPAN Systems''. IEICE TRANSACTIONS on Communications. Vol. E94-B. 2011. pp.1332-1338. Available in: http://soc.inha.ac.kr/images/High-Throughput_Low-Complexity_Four-Parallel_Reed-Solomon_Decoder_IEICE%282011.05.01%29_published.pdf. Consultada el 05 de abril de 2011.         [ Links ]

4. L. Hanho. ''High-speed VLSI architecture for parallel Reed-Solomon decoder''. IEEE Trans. Very Large Scale Integr. Syst. Vol. 11. 2003. pp. 288-294. Available from: http://soc.inha.ac.kr/images/Itvlsi03_lee.pdf. Consultada 10 de noviembre de 2010.         [ Links ]

5. P. Sobe. Parallel Reed/Solomon Coding on Multicore Processors. In Proceedings of the 2010 International Workshop on Storage Network Architecture and Parallel I/Os (SNAPI '10). IEEE Computer Society. Washington DC, USA. 2010. pp. 71-80, Available from: http://storageconference.org/2010/Papers/SNAPI/8.Sobe.pdf. Consultada 11 de agosto de 2011.         [ Links ]

6. C. Sandoval. ''Multiplicador Paralelo en Campos Finitos de Galois GF (2m) Aplicado a Códigos Reed Solomon con longitud ajustable sobre FPGA''. Congreso Internacional de Investigación UC. Vol. 1. 2010. pp. 42-48.         [ Links ]