ARTÍCULO ORIGINAL

Variable frequency harmonic vibration suppression using active vibration absorption

Supresión de Vibración Armónica de Frecuencia Variable Usando Absorción Activa de Vibraciones

Francisco Beltrán-Carbajal*

¹Departamento de Energía, Unidad Azcapotzalco, Universidad Autónoma Metropolitana. Av. San Pablo N.° 180, Colonia Reynosa Tamaulipas. C.P. 02200. México D.F., México.

^*Corresponding author: Francisco Beltrán Carbajal, e-mail: fbeltran.git@gmail.com

(Received January 16, 2014; accepted June 26, 2014)

Abstract

Passive dynamic vibration absorbers have been extensively used for harmful vibration attenuation in many practical engineering systems. The applicability of these passive vibration absorption devices is limited to a specific narrow operation frequency bandwidth. In this article, a novel active vibration absorption scheme is proposed to extend the vibration suppression capability of a passive mass-spring-damper absorber for any excitation frequency, including interest resonant harmonic perturbation forces. The central foundations of a passive absorber are exploited in the design stage of the presented absorption scheme. Thus, the active absorption device applies forces on the protected mechanical system that counteract the unknown perturbation forces, conserving the vibration attenuation property of the passive absorber. The perturbation force is estimated on-line using an extended state observer proposed in this work. Simulation results are included to show the efficiency of the active vibration absorption scheme to reject completely unknown resonant and chaotic forced vibrations affecting the primary mechanical system, and to prove the effectiveness of the estimation of exogenous perturbation forces.

Keywords: Mechanical vibrations, dynamic vibration absorbers, active vibration absorption, force estimation

Resumen

Los absorbedores dinámicos pasivos de vibraciones se han utilizado ampliamente para atenuación de vibraciones dañinas en muchos sistemas de ingeniería prácticos. La aplicabilidad de estos dispositivos de absorción pasiva de vibraciones se limita a un ancho de banda angosto y especifico de frecuencias de operación. En este artículo se propone un nuevo esquema de absorción activa de vibraciones que permite extender la capacidad de supresión de vibraciones de un absorbedor masa-resorte-amortiguador pasivo para cualquier frecuencia de excitación, incluyendo fuerzas de perturbación armónica resonantes de interés. Los fundamentos centrales de un absorbedor pasivo se explotan en la etapa de diseño del esquema de absorción propuesto. Así, el dispositivo de absorción activa aplica fuerzas sobre el sistema mecánico primario que contrarrestan las fuerzas de perturbación desconocidas, conservando la propiedad de atenuación de vibraciones del absorbedor pasivo. La fuerza de perturbación se estima en línea usando un observador de estado extendido propuesto en este trabajo. Se incluyen resultados en simulación para mostrar la eficiencia del esquema de absorción activa de vibraciones para rechazar vibraciones forzadas resonantes y caóticas completamente desconocidas afectando el sistema mecánico primario, y para probar la efectividad de la estimación de fuerzas de perturbación exógenas.

Palabras clave:Vibraciones mecánicas, absorbedores dinámicos de vibraciones, absorción activa de vibraciones, estimación de fuerza

Introduction

Mechanical vibration is a quite common problem in numerous applications of practical engineering systems. Vibrations can cause diverse troubles as material fatigue, rapid wear of machine parts, excessive noise, poor finishes of manufactured products, loosening of fasteners, efficiency loss, discomfort to people and malfunction of instrumentation [1]. A low cost practical technological solution to the harmful vibration problem consists on the use of passive dynamic vibration absorbers to attenuate vibrations of a primary or main mechanical system below acceptable levels. The dynamic vibration absorbers are also known in the literature as anti-vibrators, vibration neutralizers, tuned mass dampers, dynamic damper, vibration absorber and shock absorber [2-4]. A vibration absorber is a devise comprising inertia, stiffness and damping elements coupled to the flexible mechanical system to be protected. This secondary or auxiliary mechanical system can be considered in the design stage of a mechanical system or incorporated to an existing system.

The passive vibration absorption devices manifest satisfactory results into a narrow excitation frequency bandwidth without the use of an external energy supply. This secondary system adds two new resonant frequencies where the forced mechanical system exhibits high vibration levels. The inclusion of optimum viscous damping into the vibration absorber is a well-known solution to increase the harmonic vibration attenuation band. However, damping could make inefficient the vibration absorption mechanism and the vibration cancellation at the tuning frequency of the absorber is not guaranteed anymore. Therefore, a passive vibration absorber is not recommended for variable frequency operation conditions involving resonant excitation forces. For these scenarios, properly controlled active vibration absorbers offer better performances (see, e.g., [5- 11] and references therein). The interested reader is also referred to the books [2-4] and references therein, where various configurations, shapes, models and applications of dynamic vibration absorbers are clearly described.

Certainly, there exist current valuable proposals on vibration control schemes using vibration absorbers reported in the literature (see, e.g., [5- 16]). Here, it is evidenced this research subject is quick active and important. Nevertheless, most of the contributions using a single mass-springdamper absorber mainly consider the vibration suppression problem for certain excitation frequencies. Thus, the efficient vibration absorption problem for on-line rejection and estimation of unknown variable resonant disturbing forces is challenging, pertinent and relevant, and its solutions admit a wide variety of real applications in the design and operation of practical engineering systems. Moreover, the estimation of exogenous forces is also a problem of high relevance in vibration control of flexible mechanical systems [17].

This paper deals with the harmonic vibration suppression problem of variable excitation frequency using active dynamic vibration absorbers. A novel simple and efficient active vibration absorption scheme is proposed to extend the applicability of a passive mass-springdamper absorber for any excitation frequency, including interest resonant harmonic perturbation forces. The presented control design approach exploits the central basis of a passive vibration absorber. Thus, different to the most of the current active vibration control proposals, in this work an active vibration absorber is seen as a dynamic controller that should apply forces on the primary mechanical system that counteract the unknown perturbation forces through the coupling mechanical elements between both systems. Moreover, the vibration attenuation property of the passive vibration absorber is advantageously conserved. The simplicity of our active vibration control scheme is an additional feature that makes this attractive. The proposed active vibration absorption scheme includes a feedback controller for reference position trajectory tracking tasks on the vibration absorber and an on-line asymptotic estimation approach of harmonic excitation forces. The perturbation signal estimation is based on the Taylor polynomial expansion of the harmonic force and the design of an extended state observer. In previous works [11, 12], the perturbation force is algebraically reconstructed by estimating its frequency, amplitude and phase parameters on-line. In this work, the force and its time derivatives up to a certain order are directly estimated. The force estimate can then greatly simplify the estimation procedure of the parameters associated with such force. The introduced design methodology can be extended for other configurations of vibration absorbers, several perturbation force types and on-line parameter identification.

Some simulation results are provided to show the efficient performance of the presented vibration absorption scheme as well as the fast and efficacious estimation of resonant perturbation forces. Additionally, the acceptable performance of the proposed active vibration absorption scheme and on-line force estimation approach were verified when the primary mechanical system is subjected to completely unknown chaotic disturbances generated by a Lorenz system. Note that, it is widely known that uncertain chaotic systems exhibit complex and unpredictable behavior and hence the state estimation is an open and challenging problem. Therefore, the synthesis of the actively controlled absorption device introduced in this paper also represents an alternative solution for real-time estimation and rejection of this kind of disturbance signals in vibrating mechanical systems. For more details on chaotic systems reader is referred to [18-20] and references therein.

Vibrating mechanical system

Consider the forced vibrating primary mechanical system with an active mass-springdamper dynamic vibration absorber shown in figure 1. The generalized coordinates are the positions of each mass, x₁ and x₂. In addition, u represents the control force input and f(t) some unknown harmonic excitation force. Here, m₁, k₁ and c₁ denote mass, stiffness and viscous damping of the primary mechanical system to be protected against undesirable harmonic vibrations. Similarly, m₂ , k₂ and c₂ denote mass, stiffness and viscous damping of the dynamic vibration absorber. Note that, when u ≡ 0 the active vibration absorber becomes only a passive vibration absorber, which is able to attenuate harmonic vibrations into a small frequency band close to its tuning frequency.

The vibration mechanical system can also be represented schematically by the feedback interconnection of figure 2. In this energetic interconnection diagram, the primary mechanical system and the active vibration dynamic absorber are modeled by Σ₁ and Σ₂, respectively. Moreover, y₁ = x₁ and y₂ = x₂ are the output variables of each subsystem.

The mathematical model that describes the dynamic behaviour of the actively controlled vibration mechanical system is then given by the set of coupled ordinary differential equations (1).

Where f(t) is a harmonic force affecting the primary mechanical system of the form (2).

Here, ω and F₀ are the excitation frequency and amplitude of the force f, respectively.

Defining the state variables as z₁=x₁, z₂=x₁, z₃=x₂ and z₄=x₂, one obtains the state space description (3).

The dynamic system (3) is stable in the case of u ≡ 0 and f ≡ 0. In fact, defining the storage function (4) as the total energy of the system.

And taking the time derivative of V along the trajectories of system (2) results in the expression (5).

Then V ≡ 0 if and only if z₂=z₄ ≡ 0, and hence z₁=z₃ ≡ 0. Therefore, from the LaSalle's Theorem [21] is proved that system (3) is globally asymptotically stable.

Strictly speaking, the active vibration control problem consists on applying to the primary mechanical system a force that counteracts the undesirable harmonic vibrations. In this contribution, the use of an active vibration dynamic absorber is proposed. Thus, the control force is transmitted from the vibration absorption devise to the primary mechanical system through the coupling mechanic elements (spring k₂). Therefore, the total active vibration suppression (z1 → 0 as t → ∞) is accomplished if and only if u_a=k₂z₃=-f(t). Then, one can conclude that the position variable of the vibration absorber follows the reference trajectory described by (6).

Thereby, a novel active vibration absorption scheme is proposed in this paper. This consists of a feedback controller (u) for reference position trajectory tracking tasks on the vibration absorber and an on-line asymptotic estimation approach of harmonic excitation forces. The reference trajectory is specified in accordance with the control force (u_a=k₂z₃=-f(t)) that allows suppressing the harmonic vibrations on the primary mechanical system. This means, the position output variable (y₂=z₃) of the vibration absorber (Σ₂) should satisfactorily follow the time-varying trajectory (z*₃(t)=-f(t)/k₂) in closed loop. Therefore, the transcendence of the proposed active vibration control approach is the applicability extension of passive vibration absorbers for variable excitation frequency conditions instead of a specific operation frequency alone. In addition, the online identification of the excitation frequency and amplitude is greatly simplified thanks to the availability of the estimated force signal.

Active vibration absorption

Consider the mathematical model (Σ₂) of the active vibration absorber described by (7).

Then, the feedback controller (8) is proposed for the tracking of some reference position trajectory y*₂ (t) on the vibration absorber.

Substitution of the controller (8) into system (7), results in the closed loop dynamics (9) of the tracking error, e₂ = y₂ - y*₂ .

with characteristic polynomial (10).

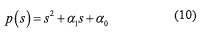
Therefore, the design parameters, α₀ and α₁, are selected so that the characteristic polynomial (10) is a (stable) Hurwitz polynomial. Hence, the global asymptotic stability of the tracking error e₂ is guaranteed. Then, the tracking of the trajectory y*₂ (t) is verified as (11), i.e.,

For the closed-loop tracking error dynamics, the reference system (12) is proposed in terms of the natural frequency ω_nc > 0 and damping ratio ζ_c > 0 desired for the active vibration absorber.

Then, the control gains can easily be computed as α₀= ω_²nc and α₁= 2ζ_cω_nc.

Evidently, the optimal vibration attenuation (x₁ = 0) in the primary mechanical system (Σ₁) is accomplished for the reference position trajectory y*₂= - f (t)/k₂. Under this scenario, the closed loop dynamic for the controlled mechanical system (1) is then given by equations (13).

Clearly, system (13) can be simplified as (14).

Therefore, e₂→0⇒ x₁→0, and thence the steady state control response is given by (15).

where and are the natural frequency and damping ratio of the passive vibration absorber, respectively.

Moreover, it is desired that ζ₂≈ 0, in order to get the maximum efficiency of the passive vibration dynamic absorber. In this case, equation (15) is simplified as (16).

Thus, one can verify from (16) that when the excitation frequency ω is equal to the natural frequency (tuning frequency) ω₂ of the passive vibration absorber, the maximum vibration attenuation (x₁≈ 0) is obtained with a small control effort (u ≈ 0). Consequently, the proposed active vibration control scheme takes into account the main application of the passive vibration absorption property as well. Certainly, the simplicity of the proposed control approach is resulted of the appropriate use of the passive vibration absorber.

Since the planned reference trajectory y*₂ (t) requires information of the harmonic force f(t)=F₀sinωt as well as its time derivatives up to second order, in next section an on-line force estimation approach is presented. The estimation is based on the design methodology of state observers presented in [22], which are robust against time polynomial perturbation inputs.

On-line harmonic excitation force estimation

It is widely known the huge usefulness of the Taylor polynomials for approximating functions in many engineering applications. Indeed, the harmonic force f(t) can locally be modeled by the family of Taylor polynomials of order r-1 described by (17) [23]:

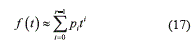
where the residual terms are negligible if t↓0 or r→∞. Therefore, one can approximately reconstruct the disturbance force signal into a short time interval by identifying the coefficients p_i [24].

Then, from (17) the r-th order mathematical model (18) for the harmonic force is obtained.

where f₁=f, f₂=f, f₃= f¨, ... , f_r=f ^(r-1). In addition, δ is an unknown bounded perturbation which considers the influence of the residual terms of the truncated Taylor polynomial expansion (17).

Thus, the local dynamics of the extended primary mechanical system is governed by (19).

Then, from (19), the extended estate observer (20) is proposed.

The estimation error dynamics is then described by equation (21).

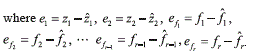
The characteristic polynomial associated with (21) is given by (22).

The observer gains, β₁, i = 0, 1, 2, ... r+1, are selected so that the characteristic polynomial (22) is a Hurwitz polynomial. Therefore, the observation error is bounded for any δ bounded [25]. Hence, estimates of the harmonic force and its time derivatives up to r-th order can be obtained by the implementation of the extended state observer (20). Note that the characteristic polynomial (22) do not depend of the coefficients p_i of the polynomial expansion (17). Thus, the observer continually self-updates and the harmonic force f(t) is locally approximated by a (r-1)-th degree time polynomial. Undoubtedly, the observer design parameters β₁ have to be chosen so that the observation error dynamics is faster than the desired closed-loop primary system dynamics as well as the highest excitation frequency of the harmonic perturbation force specified to be rejected.

Simulation results

In order to verify the efficiency and effectiveness of the proposed active vibration absorption scheme, some computer simulations were carried out on a mechanical system with a dynamic vibration absorber characterized by the realistic parameter set described in table 1.

First of all, the high performance of the passive vibration absorber (u ≡ 0) is shown in figure 3. In this scenario, the primary mechanical system is perturbed by the harmonic force f(t)4sin(9.65t) N and the passive vibration absorber tuned at . Clearly, the passive absorber cancels the harmonic vibration affecting the primary system response. Evidently, this is because the excitation frequency, ω=9.65rad/s, coincides with the tuning frequency (ω₂) of the vibration absorber.

On the other hand, figure 4 manifests the unsatisfactory performance of the passive vibration absorption when the primary system is disturbed by the resonant frequency excitation f(t)=4sin(8.35t)N. This operation condition notoriously induces very large vibration amplitudes which is an unacceptable situation. Thus, an active vibration absorber is recommended for variable frequency operation conditions inside the working bandwidth of the equipment, including resonant frequency vibrations.

Figure 5 presents the efficient performance of the proposed active vibration absorption scheme based on the controller (8) and extended state observer (20). Here, the satisfactory vibration suppression on the primary mechanical system subjected to the resonant excitation force f(t)=4sin(8.35t) is verified.

The effective estimation of the harmonic force is displayed in figure 6. The small estimation error of the harmonic force, e_f = f - f_e, is clearly visible. For this assessment, a third order Taylor polynomial family was chosen for the harmonic force reconstruction. The characteristic polynomial for the sixth order estimation error dynamics was set to be of the form (23).

Where the natural frequency ω_no and the damping ratio ζ_o were chosen so that the estimation error dynamics be faster than the desired closed-loop primary system dynamics and the excitation frequency. Thus, these gains were set as: ω_no= 300 rad/s and ζ_o=0.7071.

Figure 7 shows the response of the control force u applied to the vibration absorber at the time of 4 s. The satisfactory tracking of the reference trajectory specified for the active vibration absorber is accomplished. Therefore, the small tracking error,, is practically zero. The control gains were selected to get a closed-loop secondary system dynamics having the Hurwitz characteristic polynomial (24), with natural frequency ω_nc=15 rad/s and damping ratio ζ_c =0.7071.

the active vibration absorber is accomplished. Therefore, the small tracking error, , is practically zero. The control gains were selected to get a closed-loop secondary system dynamics having the Hurwitz characteristic polynomial (24), with natural frequency ωnc=15 rad/s and damping ratio ζc =0.7071.

with a=10, b=30, c=1, and initial conditions η₁(0)=-10, η₂(0)=-10, η₃(0)=-10.

Figures 8, 9 and 10 describe the acceptable performance of the proposed active vibration absorption scheme using disturbance force estimation generated by the chaotic system of Lorenz (25). The attenuation of chaotic forced vibrations is verified in figure 8. The satisfactory estimation of the excitation force is clearly visualized in figure 9. Moreover, the control force applied to the vibration absorber is shown in figure 9. Here, the effective tracking of reference trajectory generated on-line and planned for the actively controlled vibration absorber is verified as well.

Conclusions

In this paper a novel active vibration absorption scheme has been proposed to extend the vibration suppression capability of a passive mass-springdamper absorber for any excitation frequency. The presented design approach considers an active vibration absorber as a dynamic controller that applies forces on the primary mechanical system that counteract the unknown perturbation forces. In this way, the active vibration control synthesis is greatly simplified and the dissipation property of the passive vibration absorption is conserved. The control force of the active absorber is transmitted to the primary mechanical system through the coupling mechanical spring. The proposed active vibration absorption scheme includes a feedback controller for reference position trajectory tracking tasks on the vibration absorber and an online asymptotic estimation approach of harmonic excitation forces as well as its time derivatives of certain order. The perturbation signal estimation is based on the Taylor polynomial expansion of the harmonic force and the design of an extended state observer. The analytical and simulation results show the robust and efficient performance of the proposed active vibration absorption scheme to reject variable frequency harmonic vibrations as well as disturbing forces generated by a chaotic system of Lorenz. The fast and effective estimation of the harmonic and chaotic perturbation forces is verified as well. Therefore, one can conclude that our active vibration absorption approach represents a very good alternative solution to the problem of variable frequency vibration suppression. In addition, the obtained results can be extended to other topologies of absorbers to attenuate vibrations due to a wide spectrum of endogenous and exogenous disturbances.

References

S. Rao. Mechanical Vibrations. 5^th ed. Ed. Prentice Hall. Upper Saddle River. New Jersey, USA. 2011. pp. 10-13.         [ Links ]

2. B. Korenev, L. Reznikov. Dynamic Vibration Absorbers. 1^st ed. Ed. John Wiley & Sons Ltd. Chichester. England. 1993. pp. 1-296.         [ Links ]

3. S. Braun, D. Ewins, S. Rao. Encyclopedia of Vibration. 1^st ed. Ed. Academic Press. London, UK. 2002. pp. 1-26.         [ Links ]

4. A. Piersol, T. Paez. Harris's Shock and Vibration Handbook. 6^th ed. Ed. McGraw-Hill. Columbus, USA. 2010. pp. 6.1-6.33.         [ Links ]

5. C. Kai, A. Huang. ''Active Vibration Absorbers Design for Mechanical Systems with Frequency-Varying Excitations''. Journal of Vibration and Control. DOI: 10.1177/1077546313478293. 2013. pp. 1-14.         [ Links ]

6. S. Chatterjee. ''Optimal Active Absorber with Internal State Feedback for Controlling Resonant and Transient Vibration''. Journal of Vibration and Control. Vol. 329. 2010. pp. 5397-5414.         [ Links ]

7. M. Tso, J. Yuang, W. Wong. ''Suppression of Random Vibration in Flexible Structures Using a Hybrid Vibration Absorber''. Journal of Vibration and Control. Vol. 331. 2012. pp. 974-986.         [ Links ]

8.P. Bhatta, A. Sinha. ''A Discrete-time, Optimal, Active Vibration Absorber''. Journal of Sound and Vibration. Vol. 268. 2003. pp. 201-208.         [ Links ]

9. P. Bonello. ''Adaptive Tuned Vibration Absorbers: Design Principles, Concepts and Physical Implementations''. F. Beltrán (editor). Vibration Analysis and Control-New Trends and Developments. 1^st ed. Ed. InTech. Rijeka, Croatia. 2011. pp. 1-26.         [ Links ]

10. F. Beltrán, G. Silva, B. Vázquez, E. Chávez. ''Design of Active Vibration Absorbers Using On-Line Estimation of Parameters and Signals''. F. Beltrán (editor). Vibration Analysis and Control-New Trends and Developments. 1^st ed. Ed. InTech. Rijeka, Croatia. 2011. pp. 27-46.         [ Links ]

11. F. Beltrán, G. Silva. ''Adaptive-Like Vibration Control in Mechanical Systems with Unknown Parameters and Signals''. Asian J. Control. Vol. 15. No. 16. 2013. pp. 1613-1526.         [ Links ]

12. F. Beltrán, G. Silva, M. Arias. ''Active Unbalance Control of Rotor Systems Using On-Line Algebraic Identification Methods''. Asian J. Control. Vol. 15. No. 16. 2013. pp. 1627-1637.         [ Links ]

13. T. Bandivadekar, R. Jangid. ''Optimization of Multiple Tuned Mass Dampers for Vibration Control of System Under External Excitation''. Journal of Vibration and Control. Vol. 19. 2012. pp. 1854-1871.         [ Links ]

14. R. Chen, T. Wu. ''Vibration Control of Base System Using Distributed Dynamic Vibration Absorbers.'' Journal of Vibration and Control. DOI: 10.1177/1077546312472923. 2014. pp. 1-12.         [ Links ]

15. R. Harik, J. Issa. ''Design of a vibration absorber for harmonically forced damped systems.'' Journal of Vibration and Control. DOI: 10.1177/1077546313501928. 2013. pp. 1-11.         [ Links ]

16. S. Saravanamurugan, T. Alwarsamy, K. Devarajan. ''Optimization of Damped Dynamic Vibration Absorber to Control Chatter in Metal Cutting Process''. Journal of Vibration and Control. DOI: 10.1177/1077546313492554. 2013. pp. 1-10.         [ Links ]

17. M. Arias, F. Beltrán, G. Silva. ''On-line Algebraic Identification of Eccentricity Parameters in Active Rotor-Bearing Systems''. International Journal of Mechanical Sciences. Vol. 85. 2014. pp. 152-159.         [ Links ]

18. X. Zhang, X. Liu, Q. Zhu. ''Adaptive Chatter Free Sliding Mode Control for a Class of Uncertain Chaotic Systems''. Applied Mathematics and Computation. Vol. 232. 2014. pp. 431-435.         [ Links ]

19. A. Senouci, A. Boukabou. ''Predictive Control and Synchronization of Chaotic and Hyperchaotic Systems Based on a T-S Fuzzy Model''. Mathematics and Computers in Simulation. Vol. 105. 2014. pp. 62-78.         [ Links ]

20. G. Chen. Controlling Chaos and Bifurcations in Engineering Systems. 1^st ed. Ed. CRC Press. Florida, USA. 1999. pp. 1-71.         [ Links ]

21. H. Khalil. Nonlinear Systems. 3^rd ed. Ed. Prentice Hall. New Jersey, USA. 2002. pp. 126-130.         [ Links ]

22. H. Sira, V. Feliu, F. Beltrán, A. Blanco. Sigma- Delta Modulation Sliding Mode Observers for Linear Systems Subject to Locally Unstable Inputs. Proceedings of the 16^th Mediterranean Conference on Control and Automation. Ajaccio, France. 2008. pp. 344-349.         [ Links ]

23. H. Sira, F. Beltrán, A. Blanco. ''A Generalized Proportional Integral Output Feedback Controller for the Robust Perturbation Rejection in a Mechanical System''. Sciences et Technologies de l'Automatique. Vol. 5. 2008. pp. 24-32.         [ Links ]

24. M. Fliess, C. Join, H. Sira. ''Non-linear Estimation is Easy''. Int. J. of Modelling, Identification and Control. Vol. 4. 2008. pp. 12-27.         [ Links ]

25. Z. Gao. Active Disturbance Rejection Control: A Paradigm Shift in Feedback Control System Design. Proceedings of the 2006 American Control Conference. Minneapolis, USA. 2006. pp. 2399-2405        [ Links ]