English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
Aiming at being economically competitive within highly demanding environmental standards, energy management was initially initiated by all types of organizations worldwide to reduce both the incurred monetary costs and their carbon footprint in their operation[1]. Lately, with the “smartization” of power grids, the citizens come into play, as they can be encouraged to shape their demand profiles to increase the sustainability of the domestic tasks[2, 3].
In order to guarantee increased access to energy resources at affordable costs, either for citizens or organizations, effective energy management policies must be implemented, together with easy-to-use computer-assisted applications for both electricity producers and end-users. However, the requirements of these applications will be fairly different for each of these to agents. On the one hand, companies may want to be capable of performing realistic simulations, as well as controlling and planning the electricity market. On the other hand, citizens have to be provided with applications that ease them to monitor and manage the energy consumption at household level. These applications are clearly under the context of the smart city paradigm, as they target citizen engagement, environment protection, and economic considerations to provide a good Quality of Service (QoS) and user experience[4].
By 2018, the average household energy consumption reported by the US Energy Information Administration has been 12,906 KWh of electricity[5], with an anual growing rate of approximately 0.9%[5]. In Europe, the figure is less than 10,000 KWh, but also significant as it represents 21.4% of the total energy consumed by households, which is 27.2% of total energy consumption in EU[6]. Temperature control and electronic and kitchen appliances are those that most contribute to the consumption (ranging from 65% to 75%), and this pattern is fairly similar worldwide, even in developing countries.
But energy efficiency at domestic level can be improved by accurately planning the usage of deferrable appliances, that is, those devices whose demand for energy can be postponed or interrupted (dishwashers, washing machines, etc.), with little-to-no impact on the QoS provided to the users[2, 3]. In this context, citizens can be aware of different electricity prices and the availability of sustainable, yet not-storable energy generated by renewable sources, to properly schedule the operation of these appliances.
The aim of this work is to extend our previous conference article[7] presented at the Ibero-American Congress of Smart Cities ICSC-CITIES 2019, which addresses the problem of planning household appliances considering user preferences. For the purpose of providing a recommendation system for the end-users, two conflicting objectives, namely maximizing the user satisfaction (measured in terms of the QoS provided with respect to the given preferences) and minimizing the total energy consumed (in terms of the total cost of the electricity bill), are considered. The novel contributions of this research include the formulation of a newly developed mixed-integer mathematical programming model of the problem. This has been addressed with an exact solver that may serve as a baseline for comparing with the EA, on the basis of the smaller instances.
This work has been developed under the context of the Cloud Computing for Smart Energy Management (CC-SEM) project[8, 9], which proposes building an integrated platform for smart monitoring, controlling, and planning energy consumption and generation in urban scenarios. Technologies such as Big Data analysis, computational intelligence, Internet of Things, High Performance Computing and Cloud Computing, and specific hardware for energy monitoring/control are the key enabling pillars of the project.
The article is organized as follows. Section 2 presents the formulation of the multiobjective household energy consumption planning and a review of related works. The proposed evolutionary approach for household energy planning is described in Section 3. The experimental analysis is reported in Section 4. Finally, Section 5 presents the conclusions and the main lines of future work.
2. The household energy planning problem
This section introduces the household energy planning problem, the multiobjective formulation addressed in this article, and a review of related works.
2.1 General considerations
The goal of the study is to develop a system to help end-users to take appropriate decisions concerning the use of household appliances in a given planning period (e.g., daily, weekly, etc.).
The problem consists in scheduling the use of different household appliances to minimize the energy household costs while considering end-user preferences (customer satisfaction). These can easily become conflicting interests[10] since the period of time in which end-users prefer to use the appliances might not be the one that minimizes the energy cost. Therefore, an optimization model that takes into account the end-user preferences, electricity prices, and the available contracted power is devised to solve this problem.
The planning period is divided in slots considering the user preferences. For every slot, each user can indicate a value that represents the priority of using a certain appliance in that time. Higher values of priority represent a higher desire of using the appliance. In case that users do not indicate their preferences, machine learning is applied to infer preferences from the analysis of historical utilization data. Classification methods can also be applied to characterize the household power consumption, regarding neighboring houses and socio-economical data, such as for other public services[11].
The problem formulation assumes that the energy cost is known for each time interval. In general, these values are publicly available from the energy companies, for example from the National Electricity Company (UTE for its Spanish acronym) in Uruguay. Also, the máximum contracted power for each user is known, from the contract details provided by the energy company. The contracted maximum power can only be surpassed by a small amount in a short period of time, without causing a short circuit. In line with informal surveys performed to energy practitioners implemented for this study, the users are allowed to use up to 30% more than the máximum energy. However, schedules that include such a surplus are penalized.
2.2 Problem formulation
The multiobjective version of the household energy planning problem addressed in this article considers the following sets:
a set of users U = (u 1 . . . u |U| ), each user represents a house in a city;
a set of minutes T = (t 1 . . . t |T| ) in the planning period;
a set of domestic appliances L
u
=
for each user u;
And the following parameters:
a parameter W u indicates the maximum electric power contracted by user u;
a penalty term ρ applied to those users that surpass the maximum electric power contracted;
a parameter
indicates the average time of utilization for user u of appliance l ∈ L
u
a parameter C t indicates the utilization cost (per kW) of the energy in time t;
a parameter
indicates the power (in kW) consumed by appliance l;
a parameter
indicates the preference of user u to use the appliance l ∈ L
u
at time t.
a parameter C t indicates the energy cost at time t.
Parameter
considers the energy consumption measurements of electrical devices reported by Kolter and Johnson[12]. For each minute of the day, in the period of a month, the user preference is defined considering how many times each appliance was turned on for each appliance at that minute. Parameter D uses consumption values of user appliances from a representative day. The usage duration of the appliance was studied, defined as the number of consecutive minutes in which it remained powered on[13].
Two alternatives are defined for defining the penalti model used for those situations in which the household consumption exceeds the maximum power contracted. The first alternative (soft penalty) is when the user excedes the maximum power contracted for less than 30% of it. This is the maximum value of energy consumption that can exist without a short circuit occurring. In that case, the solution is penalized by a 30% of ρ. The second scenario (hard penalty) is when the user exceeds the máximum power contracted in a value greater than or equal to 30%. Therefore, those plannings are penalized entirely by the penalty term ρ.
Lets consider the binary variable
that indicates if user u has appliance l ∈ L
u
turn on at time t; and variable
that indicates the time period in which user u has appliance l ∈ L
u
turned on continuously (without intermediate turn off) from time t.
= m - j with m = max
∈ (t, r)
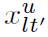= 1. Additionally, lets consider binary variables
which is 1 when the continuous usage appliance l by user u from time t is equal to or larger than the average time of utilization for user u of appliance l ∈ L
u
, 0 otherwise;
which is 1 when the consumed energy by user u at time t is excedes the maximum power contracted by that user, 0 otherwise; and
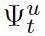which is 1 when the consumed energy by user u at time t is exceeds in more than 30% the maximum power contracted by that user, 0 otherwise.
Then, the problem can be formulated as a mixed-integer programming (MIP) model as follows:
Subject to
The problem proposes finding a planning function X =
for the use of each household appliance that simultaneously minimizes the cost of the total energy consumed, i.e., Equation (1) which include the charge for energy consumption and the penalization for exceeding the maximum power contracted, and maximizes the user satisfaction defined in Equation (2) (given the users’ preference functions). In regard to restrictions, Equation (3) establishes the length of the interval of time that each appliance will be turn on for each user at each time slot. Equation (4) sets a boundary condition for variable
. Equation (5) ensures that the length of time an appliance will be on does not exceed more tan required by the user. Equation (6) sets
to be one when the length of time an appliance will be on is equal to the required by the user. Equation (7) enforces
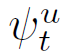to be one if the user exceeds the maximum power contracted (soft penalty). Equation (8) enforces
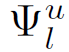to be one if the user excedes the maximum power contracted for more than 30% (hard penalty). Equation (9)-(12) establish the binary nature of the variables. Equation (13) establishes that
is a non-negative continuous variable.
Equation (3) is not linear. In order to get a linear model, linearization of[14] is applied to obtain a linear model without increasing the number of integer variables. Therefore, continuous variable
is introduced and Equation (3) is replaced by Equation (14)- (18).
2.3 Related works
The analysis of the related literature allows identifying several hardware- and software-based methods for household energy consumption characterization and planning. The main related works are reviewed next.
The main line of work related to the proposed research has been developed by Soares et al., who studied the household electricity demands and categorized a set of appliances, according to their use and management strategies that can be applied to them[15]. An initial work[2] introduced a model based on integer non-linear programming for energy utilization planning, with the aim of reducing cost. The authors applied an EA to minimize the cost of invoice and violations to the maximum contracted power. The EA allowed to reduce up to 40% the energy cost for the users with respect to a reference scenario without demand management. Later, the authors proposed minimizing cost and maximizing user satisfaction[3], which is the main motivation for the work proposed in our research. Results showed that the cost reduction was 22-24%. However, no trade-off solutions were computed, so different users with equal contracted power and equal preferences should adapt to the same planning. Additionally, no studies were carried out in different urban levels (buildings, neighborhoods, etc.) or used real data.
Our previous work[16] presented a hardware and software platform for intelligent monitoring and planning of energy consumption in homes. The proposed system integrates a hardware controller for energy efficiency, a communication protocol to improve data transmission, and a software module for planning and managing household devices.
The proposed solution was implemented applying the Internet of Things (IoT) paradigm, allowing the integration of computational intelligence techniques. A greedy algorithm was proposed for planning, considering user preferences and a maximum allowed power consumption. Results showed that it is possible to reduce the energy consumption of a water heater to 38.9% and that two water heaters and an air conditioner can be optimized simultaneously without reducing QoS. These results suggest that the proposed approach is useful for energy consumption planning in homes.
Bilil et al. proposed a characterization of household appliances and a dynamic planning method for collaborative microgrids[17]. Two multiobjective optimization problems were studied, accounting for the activation and power profiles of appliances. A simulation procedure was applied to generate the instances of these problems and NSGA-II was used to solve them.
The instances consisting in 40 microgrids that include a flexible deferrable appliance, such as a water heater, and a non-flexible one (i.e., dishwasher). For the experiments, a residential load curve based on U.S. user profiles was used. The results showed that the load curve can indeed become very flat by applying the proposed bi-level multiobjective optimization scheduling approach.
Geem et al.[18] proposed an Harmony search optimization algorithm to define charging schedule of an energy storage system with renewable power generators under dynamic electricity prices and demand charge policy.
Although heuristic methods were generally used to solve energy scheduling problems (mainly due to the associated computational complexity[19]), other methods have also been applied to similar problems in the related literature. For example, Guan et al. proposed an exact formulation for configuring the household energy planning while considering a variety of energy supply sources and electric demands[20]. They solved the problem using CPLEX while considering uncertainty associated with energy supply sources. Barbato et al. modelled a problem of household energy planning with a non-cooperative game theoretical approach[21] where they considered dynamic energy prices in order to induce a reduction of demand peaks.
The analysis of the related works indicates that there is room to contribute with solutions focused on the development of systems to implement the management of domestic demand through the integration of IoT technologies and computational intelligence algorithms.
3. The proposed EA for household energy planning
This section describes the proposed EA to solve the household energy planning problem.
3.1 Evolutionary algorithms
EAs are stochastic techniques that emulate natural evolution to solve optimization, search, and learning problems. They are useful for solving complex real-world problems in multiple application áreas[22].
An EA is an iterative The initial population is generated by applying a random procedure or using a specific heuristic for the problem to be solved. Each individual encodes a tentative solution to the problem and has a fitness value that determines its suitability to solve the problem. The goal of the EA is to improve the fitness of individuals in the population. In order to achieve this objective, evolutionary operators are applied iteratively, such as the recombination of parts of two individuals and the random mutation of an individual’s coding. These operators are applied to individuals selected according to their fitness, thus guiding the EA toward tentative solutions of higher quality that replace old individuals.
The stop criterion usually involves a fixed number of generations, a quality level on the fitness of the best individual, or detecting convergence. The EA returns the best solution found in the iterative process, taking into account the fitness function considered for the problem.
Algorithm 1 presents the generic schema of an EA with a population P.
3.2 The proposed EA for household appliances planning
The main features of the proposed EA for household appliances planning are described next. Solution encoding.
A problem-specific encoding is used to represent solutions. The proposed encoding considers for each user a vector X = (x 0 , x 1 , . . . , x T ), where T is the total number of timesteps (i.e., minutes) in the planning period. Each element xj in the encoding is a vector of binary values xj = (b 1 , b 2 , . . . , b L ), where L is the number of appliances considered in the planning and each value b i indicates if the appliance is on on timestep j.
Figure 1 presents an example of solution encoding for an instance of the problem considering five appliances. In the example, at timestep (minute) i, appliances #1, #2, and #5 are ON, while appliances #3 and #4 are OFF.
Fitness assignment. The fitness function of the proposed EA (F) corresponds to a linear aggregation of the power consumption and user satisfaction functions:
Several combinations of weights (α, β) were studied in order to properly weight each objective function and provide a useful search pattern. The main results of the analysis are reported in Section 4.2. The combination that allowed computing the best results was (α = 0.65, β = 1). Initialization. The population of tentative solutions is initialized by applying a randomized method that assigns to each appliance a probability γ = 0.6 (value tuned in preliminary experiments) to be ON at each time step, following a discrete non-uniform distribution. Assigning a slightly larger probability to each appliance to be ON than to be OFF allows starting the evolutionary search for a more diverse set of solutions. The value of γ was set to provide an equal pressure to both objectives, considering the weights defined in the previous paragraph. Selection.
The standard tournament selection was applied in the proposed EA. Preliminary experiments demonstrated that tournament selection provides an appropriate selection pressure to guide the search. After a preliminary configuration analysis, the size of the tournament was set to two individuals, and the best of them is selected. Evolutionary operators. Ad-hoc evolutionary operators were conceived to provide efficacy and diversity to the search, working with the proposed solution encoding.
The proposed evolutionary operators are:
Recombination. An ad-hoc version of the Single Point Crossover operator was conceived to recombine solutions. A cutting point is selected for each user and a new planning is created for each user, using information from the first parent (before the cutting point) and from the second parent (after the cutting point). Figure 2 presents an example of the application of the proposed recombination operator between two solutions for a problem instance with three users and six appliances for each user.
Mutation. The mutation operator modifies the current state of an appliance. First, a specific time interval is randomly selected for every user, according to a uniform distribution. An appliance is then randomly selected (applying a uniform distribution) from all belonging to that user, and its state is changed (on/off or viceversa). Figure 3 presents an example of the mutation operator.
3.3 Development and execution platform
The evolutionary approach was implemented using the ECJ library, a Java-based evolutionary computation system developed at George Mason University (cs.gmu.edu/~eclab/projects/ecj). ECJ includes easily modifiable classes for solving optimization problems.
The experimental evaluation was performed on a Dell Power Edge server, Quad-core Xeon E5430 processor at 2.66GHz, 8 GB RAM, from Cluster FING, Universidad de la República, Uruguay[23].
4. Experimental analysis
This Section presents the experimental analysis of the proposed EA for household energy consumption planning in order to test the capability of developing an automated recommendation system for end-users. As aforementioned, this is a relevant problem for both energy companies and citizens under the novel smart city paradigm.
4.1 Problem instances
A set of six problem instances was built using real data [Table 1].
First of all, a set of representative deferrable appliances of household consumption was chosen. For this purpose, the following information was consulted: i) the categorization of household appliances according to their operating profiles and purposes[2]; ii) the average and máximum time of use of each appliance -which was computed (calculated from real energy household consumption data of the REDD dataset[12]) to determine those appliances that mostly contribute to the overall energy consumption-; and iii) other complementary parameters, such as, the number of times that the appliance is turned in a month, the number of households where each appliance is present, the frequency of activation, etc. At the end of this procedure, six deferrable appliances were selected: dishwasher, microwave, dryer, air conditioning, oven, and refrigerator. The planning period is one day.
From REDD dataset[12], data of the energy consumption of one month was retrieved studied for the selected appliances. This data, that in REDD dataset[12] is sampled every three seconds, was discretized in fifteen minutes time intervals. For each time interval and for each appliance, the user’s preference to have that appliance turned on was defined as directly proportional to the number of days in which that appliance was turned on in that time interval. Since considerable differences were detected in the usage profile of the appliances on weekdays and weekend, different instances were made for these two parts of the week. Finally, data of the energy prices and maximum allowable electric power that can be used by a household were retrieved from the National Electricity Company (UTE) in Uruguay (https://portal.ute.com.uy).
4.2 Linear aggregation of EA fitness function
Since the presented problem in Section 2.2 aims at simultaneously minimizing costs and maximizing user satisfaction, a linear aggregation approach was used for handling this biobjective nature in the fitness function of the EA as stated in Equation (19). An analysis was performed to set the best values of α and β. Particularly, the candidate values considered for α were {0.3, 0.65, 0.75, 1.0} and β were {0.3, 0.5, 1.0}. For this analysis, the EA was executed over three medium-size instances of the problem (two, four, and six devices). Table 2 reports the mean and interquartile range (IQR) of the best fitness value computed in 30 independent executions of the proposed EA for the three instances solved, using the studied configurations.
A graphical example is shown in Figure 4, in which the trade-off analysis of different combinations of (α,β) are presented for solutions for instance #3. These results are representative of those obtained for other tested instances. Finally, the combination (0.65,1.0) was chosen since it allowed computing the best trade-off solutions regarding user satisfaction and energy cost.
4.3 Baseline algorithms for results comparison
Two baseline heuristics strategies were implemented for evaluating the results of the proposed EA for household appliances planning: a greedy algorithm and a Business-as-Usual (BaU) planning strategy, which are described next. Greedy planning strategy. Greedy algorithms iteratively build solutions based on a taking optimal local decisions in each step. For this particular case, a greedy algorithm from the literatura[16] was adapted.
The proposed strategy searches the best time intervals to switch on each appliance dk, according to the user satisfaction and cost, considering the linear aggregation fitness function used for the EA (Equation (19)] using α = 0.65 and β = 1 (Algorithm 2). BaU planning strategy. The BaU strategy proposes assigning ON times to each appliance without planning considering only user satisfaction. These plannings have good user preference values, but suboptimal cost values.
The model presented in Section 2.2 is a combinatorial optimization problem. Although this kind of problems is known to be time-consuming for exact methods, specially for real-world instances as the one used in this paper[24], the EA solutions are also compared with the exact resolution for small instances to validate the results. The MIP model is solved with Gurobi 8.1.1.[25] through Pyomo as modelling language[26]. For the purpose of comparison, the same combination (α,β) that was used in the linear aggregation of the EA was used is Gurobi.
4.4 Parametric configuration analysis
EA parameters must be adjusted to determine the configuration that allows computing the best results. The analysis was performed over three problem instances, different from those used in the evaluation to avoid bias. After an initial evaluation, the population size was fixed at 150 individuals after preliminary experiment[27].
Three relevant parameters of the proposed EA were studied: number of generations used as stopping criterion (G), recombination probability PC and mutation probability PM. Candidate values for each parameter were: PC ∈ {0.1, 0.25, 0.5}; PM ∈ {0.1, 0.05, 0.01}; and G ∈ {2, 500, 5, 000, 10, 000}.
All combinations of parameter values were studied by performing 50 independent executions of the proposed EA for the three problem instances considered in the analysis. The metric considered in the analysis was the linear aggregation fitness function defined in the previous subsection.
The methodology for selecting the best configuration included: i) the Shapiro-Wilk statistical test was applied to check normality, taken as a null hypothesis that the results followed a normal distribution; as p-values less than 0.05 were obtained, the null hypothesis was discarded and it was assumed that the fitness results follow a non-normal distribution; ii) the Friedman’s rank test was applied, taken as a null hypothesis that the fitness distributions for the different configurations were not different, as p-values less than 0.05 were obtained, the null hypothesis was discarded and the results significantly differ from each other.
Table 3 reports the fitness values computed in the parameter setting experiments for a representative problem instance. Overall, the best results (i.e., largest fitness median and also lower IQR) were obtained using configuration #11 (values G = 10, 000, pC = 0.1, and PM = 0.1). Henceforth, these values were used in the validation experiments of the proposed EA.
4.5 Experimental results
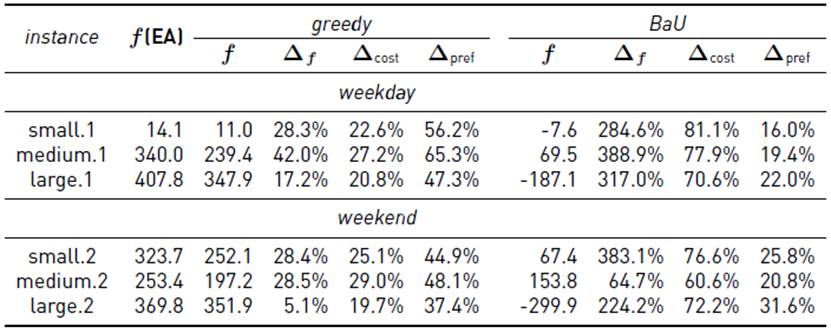
Table 4 reports the median of the best fitness computed by the EA and the comparison with the reference heuristics algorithms. The relative improvement on fitness values (Δ f ) and on each objective function (Δcost, Δpref) over each reference algorithm refA is computed as Δ = (f(EA)−f(refA))/f(refA).
Results in Table 4 indicate that the proposed EA is able to improve significantly over the greedy algorithm regarding the fitness values.
Considering the baseline results computed by the proposed greedy algorithm, improvements of up to 42.0% were obtained in instance medium.1. Results also suggest that consumption patterns during the weekend are harder to plan for the EA, as the improvements over the greedy algorithm reduced to 5.1% in instance large.2. This can be explained due to the interactive utilization of household appliances in weekends, when people are at home a significantly larger periods than in weekdays. Regarding the improvements on user satisfaction and cost, the plannings computed by the proposed EA allow reducing more than 20% the electric bill, and preferences improve more than 40% in all the studied scenarios.
The EA computed significantly cheaper plannings tan those of BaU, which systematically failed to provide good cost values, indicating that users do not take the correct decisions to turn on home appliances in this regard, and they can benefit of having an automated planning offered by a recommendation system. In addition, preferences on the solutions computed by the EA were 16-31% better than BaU. The obtained improvements over a BaU strategy are consistent with results reported in previous works for a reduced subset of home appliances (air conditioner and water heater)[16].
On the other hand, Gurobi was applied to the smaller instances with a execution timelimit of 1,800 sec: in small.1 obtained a fitness function of 17.3 (-18.5% difference with the EA) with an optimality gap of 9.79%, and in small.2 obtained a fitness function of 1,320.36 (-75.48% difference with the EA) with optimality gap of 0.23%.
The obtained results suggest that the proposed evolutionary approach is accurate for computing household energy consumption plannings accounting for both energy costs and user satisfaction at the same time in comparison to the baseline heuristics. The proposed approach is a first step towards designing an intelligent recommendation system for end-users.
5. Conclusions and future work
This article presents a mathematical formulation based on mixed-integer programming to address the problem of household energy planning that aims to optimize the energy cost, which is affected by an electricity rate that varies along the day, and the user preferences. As a first approach to develop an automated recommendation system for end-users, this is a relevant problem for both energy companies and citizens under the novel smart city paradigm.
A specific EA was proposed to solve the problem, simultaneously optimizing both criteria using a linear aggregation multiobjective function and ad-hoc evolutionary operators. A set of six realistic problem instances built using real data were considered in the experimental evaluation of the proposed EA. The analysis compared the EA results with two baseline planning heuristic methods (greedy and business-as-usual) and an exact approach based on Gurobi for small instances.
The experimental results showed that the proposed EA is able to compute accurate plannings, accounting for significant improvements on the problem objectives in comparison to the baseline heuristics. Regarding the baseline greedy algorithm, improvements of up to 42.0% were obtained in the proposed multiobjective function, accounting for an average reduction of more than 20% in the energy consumption (and thus, on the electric bill) and preferences improved more than 40% in all the studied scenarios. Regarding the BaU strategy, the EA computed significantly cheaper plannings and user preferences improved up to 31%, in line with previous results from our research group. The exact approach was able to compute better solutions but consuming a larger amount of resources.
The obtained results suggest that the proposed evolutionary approach is accurate for computing household energy consumption plannings accounting for both energy costs and user satisfaction at the same time. Overall, the proposed algorithm showed to be effective for addressing the considered optimization problem. The analysis demonstrated that users can significantly benefit of having an automated planning offered by a recommendation system.
Table 4 Experimental results: fitness values and improvements of the proposed EA over the baseline greedy algorithm and the BaU strategy
The main lines for future work are related to study explicit multiobjective algorithms to solve the problem, in order to compute several trade-off solutions at the same time. The problem formulation can be extended to include the noisy nature of user preferences in order to define an uncertainty optimization problem. In this regard, robust evolutionary approaches should be studied to solve this problem variant. Another important research line is to continue enhancing the exact resolution either by implementing more advanced multiobjective approaches (such as augmented epsilon constraint method) or considering stochastic variations of the exact model with extensive formulation. Future work also should include a more extensive computational experimentation to calibrate the parameters of the EA and a set of formal surveys to decision-makers (including users and practitioners) to estimate more accurately some of the inputs of the model (such as, the usage patron of the appliances by the users’ and the maximum amount of energy that can be used before producing a shortcut).
