I. INTRODUCTION
Currently, energy consumption is increasing exponentially due to the large number of new devices, which also implies an increase in the cost of energy consumption. Hence, the flow and availability of energy is fundamental for the interaction between supply and demand of energy systems, such importance is reflected on the behavior of energy production, import, export and consumption by sources and sectors, the latter being a fundamental part in the planning to ensure efficient energy production and consumption [1], [2]. For this reason, smart grids (SG) are applied in advanced measurement infrastructure (AMI), which allow to develop analysis of the electrical energy consumption profile in any environment [3], [4]. Therefore, given the importance of the energy system, it is necessary to implement energy consumption prediction systems that allow adequate planning of electricity consumption to reduce costs; and resource optimization, including the development of models that allow the scaling of networks in response to the demand of energy consumption [5], [6], [7].
According to the aforementioned, there are several methods that allow energy consumption forecasting, however, most of them can result in high computational processing due to the mathematical process inherent in these methods [7], for example, among the various methods is the use of artificial neural networks (ANN) that offer temporal data prediction through adaptive learning, self-organization, fault tolerance, and real-time operation allowing to monitor and track the future behavior of electrical energy consumption or other physical phenomena [8], [9]. The availability of the data universe to be used in a predictive system based on neural networks is extremely important because it allows a better system training with a low error in the prediction [10].
On the other hand, wavelet neural networks (WNN) allow to use the benefits of neural networks combined with the wavelets [11], [12] and using a smaller data universe due to the wavelet decomposition in several levels on the same wave, hence reducing storage and processing resources [13]. However, there are mathematical methods such as the use of Potential Polynomials of Degree One (P1P) that correspond to a computationally efficient mathematical model due to its ability to work even with data compression methods such as Compressive Sensing (CS), which allows using a source compression process prior to data transmission [14], [15], [16].
According to the aforementioned, electricity consumption data have time series characteristics, therefore, there are several methods that allow the projection of the electricity consumption profile. The various methods aim to predict future events, using mathematical models capable of capturing the most important trends of a Smart Grid and thus contributing to its management. The importance of predictive analysis in Smart Grid is associated with the use of Big Data in recent years due to the large amount of information collected through AMI, some of the advantages of using Big Data in Smart Grids are:
Restore service promptly in the event of a service interruption
Reduce operating costs
Reduce consumer costs
Reduction in peaks demand
Greater system efficiency
Greater security
Therefore, the objective of the case study is to identify the most efficient prediction method considering two neural network structures under three different training methods, contrasting them with the prediction obtained by P1P and WNN, and giving a continuation to the research done by [14]. The metrics analyzed correspond to the mean square error and the computational capacity through Big-O notation [13], [14], [17], [18], thus establishing the advantages in the implementation of each predictive system. Through this analysis, this case study seeks to develop a consumption prediction platform by obtaining data from the AMI network based on WNN as a first stage of prediction, so that educational institutions can evaluate and reduce their electricity consumption.
II. METHODOLOGY
A. Data Processing
Data was collected from 4 smart meters, which are connected to a smart metering network (AMI). This system collects information in 15-minute intervals, generating 96 electrical profile data per day. In addition, a 74-week universe was used with parameters such as voltage, current, accumulated electrical energy, accumulated apparent power, accumulated reactive power, and maximum power demand consumed.
In addition, the information is organized by separating the data for each day of the week and differentiating holidays, as the profile statistics changes [ref p1p]. In this context and due to the amount of information, the Big Data paradigm was applied using sorting methods to find the irregular data. The applied process is described in Fig. 1 .
After having a universe of data without irregularities, the information can be processed using a three-dimensional matrix structure as shown in Figure 2, where the structure for 8 weeks of information is identified in each matrix. Hence, through the 74 weeks obtained by the intelligent measurement system of the Educational Institution for which the prediction platform was developed; 66 sub matrices of 8 weeks were obtained by displacing 1 new week to the previous matrix. This information grouping process facilitated the subsequent analysis with the different prediction techniques used, since each day of the week presents different statistics.
This matrix organizes the data and is developed through the use of a target signal which is the daily electricity consumption profile [14],[16],[19],[20] and which the present case study starts from.
B. Potential Polynomials of Degree 1
The P1P mathematical model allows to obtain data projection by means of polynomial regressions and it also shows characteristics of simplicity and low computational cost in terms of temporal data prediction. This mathematical model has low error and high-performance characteristics in the prediction of electricity consumption data [19]. The objective of this method is to use input data with an unknown internal function to generate a future estimation value. In addition, [14] shows how this method is employed for the projection of electricity consumption data.
The prediction by P1P is governed by equation (1) and (2).
C. Neural Networks for Data Projection
The projection of electricity consumption data can work with feedforward neural networks and recurrent neural networks, the former being the most suitable for predicting the next value in a time series of data [21]. In this way, neural networks allow knowing the future behavior of the electricity consumption profile using different historical records obtained by the AMI network [22]. Then, according to the characteristics presented by the consumption profile and the reviewed literature, it was decided to use error Backpropagation and Cascade-Correlation (CASCOR) algorithms [18], [23], [24] together with the downward gradient, Resilient Backpropagation and Levenberg-Marquardt training functions [25], [26], [27], [28].
The training method for the Levenberg-Marquardt algorithm is defined by equation (3) [29].
Where J is the Jacobian matrix containing the first derivatives of the squared error with respect to each neural network parameter. Also, in equation (3), if λ tends to zero, Newton's method is obtained using the approximate Hessian; moreover, if λ is very large, it tends to behave in a manner approximating to the downward gradient method. It is advisable to start λ with a high value so that as the algorithm progresses λ decreases to obtain an acceleration in the convergence to the minimum.
As an alternative, it was also decided to work with wavelet neural networks to take advantage of the decomposition of the signal into different levels, through the wavelet functions in order to reduce the computational complexity, which allows multi-scale processing proper to the use of wavelets [30].
For the descending gradient method, a learning rate η = 0.01 was used, which determines the speed of training or convergence, as shown in the mathematical model of the previous section.
On the other hand, the parameter for the Resilient Back Propagation method was used according to the mathematical model presented in [28], where the values shown in equations (4) - (6) were used.
In order to analyze the optimization method through the Levenberg-Marquardt algorithm, a damping factor of λ = 0.2 was used, and according to [30] the initial value reveals a behavior similar to the downward gradient method. The value of λ decreases as the number of iterations of the network training progresses. Thus, as λ decreases, it behaves similarly to Newton's method, in accordance with the needs of the mathematical model shown in equation (3).
D. Training of the neural networks
For each of the implemented neural networks, a total of 8 weeks were used in the input layer considering only working days (Monday to Friday) with a total of 40 days, each containing 96 samples collected by the AMI network (Figure 1).
In order to keep the same ANN and WNN entries, 10 days were used as input data. Therefore, for the WNN, each of these days were broken down into 3 different levels using wavelets, hence obtaining 4 inputs to the neural network for each of the 10 days, thus having a total of 40 days as input data matrix for the neural network. In addition, 15 neurons were used in the hidden layer of the neural network to obtain a lower mean square error according to [17].
In the output layer there are 5 nodes, each of them represents a predicted weekday from Monday to Friday, each of these is a vector with 96 data corresponding to a sampling of every 15 minutes.
On the other hand, the wavelet function used is Daubechies, which according to [18] offers favorable results when employing it in WNNs.
II. ANALYSIS OF RESULTS
The performance analysis of the neural network in contrast with the performance of the P1P and WNN prediction method is supported by the results obtained using the mean square error in the correlation between the power consumption data and the projected data in addition to the Big-O notation. For the analysis case of Big-O, the number of neurons used in the neural network versus the time taken to train each ANN structure mentioned are used as parameters.
The P1P-based projection for the electrical consumption profile shows a fair similarity to the actual values. However, details are lost in the resolution of local maximum or minimum as shown in Fig. 3 -a. Projection methods based on conventional neural networks or wavelet neural networks demonstrate a much more accurate projection. Fig. 3 -b shows that the signals projected by the different types of training are closer to the trend of the target wave.
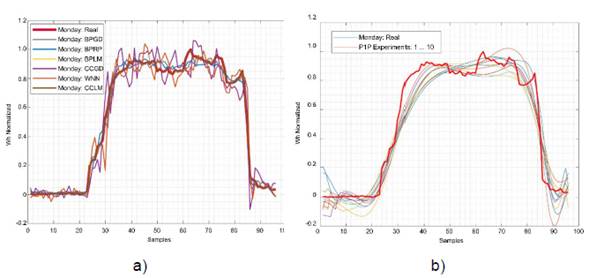
Fig. 3 Consumption profile. a) with conventional predictions and wavelet neural networks. b) with polynomial predictions.
A. Mean Squared Error (MSE)
Fig. 4 shows that the training method with the lowest possible error was Levenberg-Marquartd with a minimum MSE of 0.2% and a maximum of 0.5% in both training methods, where the MSE curve stabilizes from iteration 50 of training, while the Downward Gradient and Resilient Backpropagation training methods in CASCOR presented the highest MSE with a minimum value of 1. On the other hand, a minimum MSE of 0.18% and a maximum of 0.28% was presented for the Resilient Backpropagation training method, obtaining a stabilization in the training after 30 iterations.
For the projection obtained by the P1P prediction method, values between 1.95% and 0.67% were obtained as maximum and minimum values, respectively.
Fig. 4 also shows that the mean square errors of this method oscillate continuously without stabilizing. For the WNNs method, a mean square error of 0.41% was obtained, demonstrating a similar error stability to the Resilient Backpropagation method since they use a similar training method.
B. System Performance
In the hidden layer, the variation was from 0 to 15 neurons, hence obtaining 15 units of processing time for each prediction method. To know the behavior of each prediction method as a function of the execution time of its algorithms, the Big-O notation was used, which indicates the performance trend of the methods with theoretically smaller errors shown in the previous point.
Fig. 5 shows that the Levenberg-Marquardt training method for both network structures, including the WNN method, demonstrate a positive exponential trend, i.e., the processing time increases as the number of neurons in the hidden layer increases. On the other hand, the Back Propagation structure with the downward gradient training method reveals an opposite trend to the Levenberg-Marquardt training method for all analyzed neural network models, including WNN. It is important to mention that for the prediction method using P1P, the MSE is practically constant in all tests.
On the other hand, the Back Propagation structure with the downward gradient training method reveals an opposite trend to the Levenberg-Marquardt training method for all analyzed neural network models, including WNN. It is important to mention that for the prediction method using P1P, the MSE is practically constant in all tests.
III. CONCLUSION
According to the results obtained, the smallest MSE value is present in the conventional neural network method with Feed Forward Back Propagation structure.
Also, the Levenberg-Marquardt training method generates a lower error at a higher computational cost; in the case of WNN, it reduces the error by offering the advantage of using a smaller amount of input data that can be decomposed by wavelets, but it demands a high hardware cost.
The results show that the projections obtained through the P1P method are less accurate than the other methods because their behavior is based on a polynomial function. However, P1P compensates this deficit through computational saving features, optimization and execution times with a low MSE (between 1 and 2%) for little data.
According to the Big-O analysis, it is verified that the performance of the prediction methods depends on the number of neurons existing in the hidden layers of the neural network-based methods. Also, it is observed that the Levenberg-Marquardt method behaves in a positive exponential manner, which expresses a longer execution time as the number of hidden neurons increases. Finally, the downward gradient training method behaves inversely, as the number of neurons in the hidden layer increases the execution time will be shorter, therefore guarantying a low MSE.






















