I. INTRODUCTION
Linja has a series of rules to play correctly, and a series of components to develop the games. Up to this point, the game has been described in general terms, as it is played with the physical board. Now, to bring it into the field of computer science, the link corresponds to the application of game theory [1], which is defined as an area of mathematics where it is possible to describe situations that represent conflicts considering that the payoff is affected by the actions of an intelligent machine. In other words, game theory is constituted based on a strong mathematical structuring for problem-solving in an organization [2].
When approaching game theory as the main factor to work with the machine, it is important to select an algorithm that allows to conduct the game process by optimizing the moves. In this case, Minimax was selected. It is a game theory algorithm used to minimize the maximum expected loss with complete information since each player knows the state of his opponent [3]. According to Muros [4], this algorithm takes care of choosing the best move for the player assuming that his opponent will choose the worst move for the player.
We aim to develop an application of the Linja game using an algorithm based on game theory. For Madbouly et al. [5], game theory is oriented towards decision-making and player interventions based on the choice of strategies to maximize winning opportunities, which allows the machine to make autonomous decisions.
Therefore, it is necessary to know the rules of the game to subsequently apply the Minimax algorithm. Its application involves managing complete information of the player states to select the best move for each one, assuming that the opponent will choose the worst one [6]. In other words, it seeks to determine and observe the optimal moves in each of the games using a programming language for graphical user interface.
With the constant expansion of society, the understanding of human beings is getting bigger and bigger and the problem of learning therapy for school students is getting more and more serious, which has brought abundant tasks to the education and management of college students [7]. With the appearance of 5th generation mobile networks (5G), the data needed by mobile devices (MDs) is explosively increasing. High-consumption, low-latency applications are huge challenges for resource-constrained Internet of things (IoT) devices [8]. In Reinhardt et al. [9] several empirical studies on collaborative learning are analysed, it found that group targets, individual responsibility, and group interaction are the essential factors of promoting learning achievement.
The importance of the application of the Minimax algorithm in Linja is based on the observation of the optimal moves of the player, considering the decision making that corresponds to each move. In this case, it is determined by the machine when competing against a real player [10]. To do this, the mathematical models is adapted to the development of games within the game using a multiparadigm programming language that works together with the tools provided and that potentially contributes to develop the game to achieve an intelligent and autonomous system [11].
Finally, Linja is a strategic board game in which the main idea is to compete by taking the pieces of the player to the opposite end of the board and making them advance more optimally than the opponent until the end of the game [12].
II. MATERIALS AND METHODS
A. Information Model and Production System (PS)
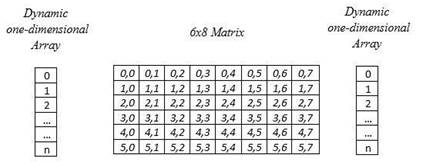
1) Data Structure (DS). For the development of the project, a data structure that relies mainly on a two-dimensional array or a matrix with 6x8 dimensions was implemented. Additionally, one-dimensional vectors have used that function as auxiliary to set the movement corresponding to the tokens and thus avoid matrix overflow.
Figure 1 shows a representation of the main DS corresponding to the 6x8 matrix with two auxiliary one-dimensional arrays of variable size, where the indexes corresponding to the positions the pieces can occupy in the structures represent the game board.
The following is a description of the basic concepts of Linja, drawn from the initial exploratory research on the game. The components of the game board are the following: 12 pieces of the same colour; 12 pieces of another colour; 7 rods or separators to assemble the board.
The playing rules are the following:
- During the turn, the player may make two moves. The first move allows the player to put a piece of his colour one line forward, except that he may not move to a line which, at that moment, contains a total of six pieces of any colour.
- The second move depends on the number of pieces in the line reached by the first move. This number, which does not include the piece that has just arrived, marks the number of lines that the player may advance using the second piece of his colour, which may be the same as the first move or different. It is forbidden to end a move on a line that already contains six pieces, but it is permitted to pass over it.
- The game ends when a player moves the last piece so all the pieces of his colour have passed over the opponent's pieces, i.e. there are no pieces of his colour left in a line or between the furthest piece and the end of the board. Not all the pieces will have reached the last line, and this is important in the game as the scoring system is based on the distance the pieces must travel.
Once a Final State (FS) is reached, the scores for each player are calculated as follows: any piece that has reached the end of the board counts for 5 points; 3 points for any piece left on the penultimate line, 2 for the previous line, 1 for the one before that, and if any pieces are still behind, they count for 0 points. The player with most points is the winner. Figure 2 shows the values corresponding to each separation, to calculate the final score of each player (see Figure 2).
2) Configuration Space (CS). At the start of the game, all the pieces must be placed on the board; six pieces of one colour are placed vertically in the first column and six of the other colours in the last column. In the same way, 6 pieces of each colour are placed in the other columns, for a total of 12 pieces placed horizontally.
The game ends when the pieces of each colour are separated in such a way that the pieces of one colour (red) are in the first four columns, and the pieces of another colour (blue) are in the next four columns. Then, to determine the winner, the score value of each column -as can be seen in the header of the board- is multiplied by the number of pieces in the column where each piece is located (Figure 3).
Starting from the game, we take the alternatives that the player has with his pieces in the first move and the first turn as a reference. In this case, the player will have seven alternatives to position a piece on a different square.
Starting from the initial node that represents the initial state (IS) and the child nodes that represent the different decisions or alternatives of the player in the initial move, we describe the potential moves that the Player One (MAX (J1)) has, taking one of the moves in the figure as a reference. It is possible to visualize many alternatives. It is also evident that alternatives will increase for Player Two (MIN (J2)) in the second move, since their advance depends on the location and the number of pieces available (Figure 4).
3) Control Strategy (CST). The Minimax algorithm was used to carry out the project, which consists of starting at the current position of the game and using the legal move generator to create the possible successive positions up to a certain limit of levels (if the game allows it, the complete game tree is developed up to the final positions).
Formally, the steps of the Minimax algorithm are the following (Figure 5):
Generate the game tree. All nodes will be generated until an end state is reached.
Calculate the utility function values for each terminal node.
Calculate the value of the upper nodes from the value of the lower ones. Depending on the level, MAX or MIN, the minimum and maximum values will be chosen, representing the moves of the player and the opponent; hence the name Minimax.
Choose the move by evaluating the values that have reached the highest level.
Figure 6a. details the Minimax algorithm. In this case, we worked on a function known as a function of minimum that uses a value "g" as a parameter to determine the current state of the token and it executes the optimal movement within the possible ones, thus returning the value that minimizes loss possibility in the movement. Figure 6b. details a function that varies according to the return value, since we worked with a function of maxima that allows us to determine the maximum gain value from the possible movements and to select the optimal. The two functions are described algorithmically, working as components to represent the tree structure of the Minimax algorithm.
Finally, Figure 6c presents the complete Minimax algorithm, including the max and min functions in a recursive way, i.e., the general algorithm but in a single function to track the moves of each player in their respective turn and determine the result of the game.
This approach leads to two interrelated research questions: (1) Can minimax search models be formulated in a way they help understanding how minimax search works? and (2) Can minimax models be used to create effective search algorithms?
The minimax search using a heuristic evaluation function is known as an effective technique for gaming. The above presents an analysis of a remarkably simple Minimax model that yields the surprising and unsatisfactory conclusion that fixed depth backing values are slightly more reliable than heuristic values [2].
4) Heuristic Programming. The heuristic to give values to the nodes of the tree and to be able to apply the Minimax technique consists of subtracting the score of the black chips (agent) from that of the red chips (human player). In this way, Minimax is guaranteed to make a decision with an optimal score for the outcome of the game.
Figure 7 shows the tree generated by the intelligent agent to decide which move to make in the Linja game, it grows to an approximate ratio of 140^n, where n refers to the depth of the tree and 140 is the number of moves that can be made on the Linja board.
The possible moves derived from the initial state are 140, having 12 pieces in the initial state and two moves per turn. Therefore, each piece’s move can be combined with that of the other, thus obtaining 12*12 = 144. There are 4 moves not performed because pieces that have already reached or exceeded the limit of the board prevent them. Hence, the maximum number of nodes reached in the tests was 2,283,383 at the maximum depth. According to the theoretical formula, it should reach 2,744,000 nodes.
B. Tools
The materials to develop the project were selected by their versatility and the easiness to unify all the parts within the same software environment, both for designing the interface and for coding the algorithm. Figure 8 shows the main interface of the "Player VS AI" game mode. In this game mode the user plays with the AI, which is based on three tactical criteria which are explained later. The implemented AI has an optimal learning level as the game unfolds. The AI learning is achieved according to the moves that the user executes, at the beginning it can execute moves according to three levels of difficulty: easy, normal, and hard. The level of difficulty is determined by the speed at which the machine learns the user's moves, i.e., the higher the difficulty, the more the AI learns as the player performs the moves in the game. In general terms, the AI moves depend on three factors: the algorithm, the level of difficulty, and the user's level during the game.
Each tactical criteria functions as an opponent and they are identified by a name, their characteristics are:
Alex: This opponent is based on the movement of the pieces located in the back, so it tends to make the advances with the farthest pieces and take advantage of the number of advances of the second move of the turn.
Drake: This opponent maintains a balanced level of movements between the forward and back pieces, so he frequently advances trying to take advantage of the first move of the turn, if possible with a forward checker to get a significant number of advances in the second move with a piece from the back.
Kira: This opponent tends to use the front pieces in her moves, so it is common that at the beginning she tries to get her pieces to the goal in a fast way by taking advantage of the first move of the turn, but sometimes she wastes the second move by not giving priority to the pieces in the back. Additionally, to selecting the game AI, the player must also select the difficulty of the game, which is based on three levels: easy, normal, and hard. The difficulty level is determined by how fast the machine learns the user's moves, i.e., the higher the difficulty of the AI, the more the machine learns.
Table 1 shows the tools used throughout the project, summarizes their main characteristics, and their proper implementation.
Table 1 Tools and materials used in the project.
| Name | Features | Implementation |
|---|---|---|
| Python | It is an open source, object-oriented programming language, very simple and easy to understand. [12] | Python in artificial intelligence (AI), allows the implementation of the Minimax algorithm with the use of appropriate libraries for the creation of an AI. |
| Pygame | A set of Python modules designed for writing video games. Pygame adds functionality in addition to the excellent SDL library. [9] | This library allows you to create the gameplay and movements of Linja with all the functions in the Python language in a simple and comfortable way. |
| Pycharm | Available as a cross-platform application, PyCharm is compatible with Linux, macOS and Windows platforms. Sitting among the best Python IDEs (Integrated Development Environment). [10] | This IDE is composed of code analysis tools, debugger, testing tools and version control options. |
| Flask | It is a Python framework and module that allows you to develop web applications easily. It has a small and easy to extend core. [13] | This framework helps in storing important information, such as moves and movements for the machine to use and memorize while playing autonomously. |
III. RESULTS AND DISCUSSION
The IS approach is discussed in an initial experimental scenario, where the tokens are located without alteration in position. Table 2 describes the positions of the tokens located in the 6x8 matrix, which in this case corresponds to the sub-index of the matrix.
Table 2 Number of advances for the second move of the first turn.
| Token colour | Subindex |
|---|---|
| Red | (0,0), (0,1), (0,2), (0,3), (0,4), (0,5), (0,6), (1,0), (2,0), (3,0), (4,0), (5,0) |
| Blue | (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (5,7), (0,7), (1,7), (2,7), (3,7), (4,7) |
Starting from the scenario, the next step is the simulation of the constraint moves set out in the playing rules. To transfer the game interface to a graphical user interface (GUI) environment using the libraries provided by the programming language, 'x' and 'y' are represented by red and blue pieces, respectively.
To validate the moves -in this case the first move corresponds to the advance in a column in the first turn- the player can move any of his pieces one square. In this example the move corresponds to the advance of the piece in the first move to subindex 1.7 of the matrix. Table 3 shows the number of squares that the player can advance in the second move once the first move of the first turn has been executed.
The second move considers the existing pieces in the column reached in the first move; in this case, column 2 is taken, which means advancing 2 squares in the second move. Figure 9 shows the moves made by player 'x' corresponding to the first turn. The first move corresponds to the piece highlighted in green, which moves from the subscript 1.7 to 1.6 of the matrix, and the second move corresponds to the piece highlighted in orange, which moves from 2.7 to 2.5.
A second experimental scenario corresponds to the arrival of the player's tokens to column 0 or column 7 of the matrix, the tokens are stored in one-dimensional arrays. Table 4 describes the positions that the tokens could have when they arrived to the target columns.
Table 4 Positions of tokens in the arrays.
| Array number | Piece colour | Array Index |
|---|---|---|
| 1 | Red | 0,1,2,3,4,5,6,7,8,9,10,11 |
| 2 | Blue | 0,1,2,3,4,5,6,7,8,9,10,11 |
A major problem in the development of the game arose when the pieces reached the first and last column of the DS, since these columns do not have a limit of tiles like the others. To solve this problem, two one-dimensional arrays are used, one for the 'x' tokens and the other for the 'y' tokens.
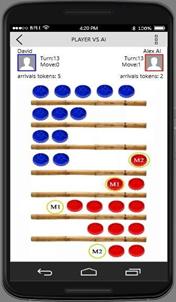
Figure 10 describes the arrival of the token with the sub index 0.6, highlighted in green, executed in the first move of the first turn of player 'y', which is stored in a one-dimensional array. In the case of the opponent's moves, which could be the machine, the aim is to find optimal moves or those that maximize the gain in each turn. For the second advance, the possible moves allow advancing four columns without losing advances, that is, maximizing the gain. The possible moves to take advantage of the second advance are shown, in this case, the algorithm or the opponent player must analyse and foresee the moves that the initial player will execute in the following turn to minimize the loss since any move triggers many possibilities to the opponent's move. The pieces marked in blue correspond to the optimal moves that the player could make; those in yellow correspond to valid moves but less effective than those in blue, and the ones in orange correspond to the worst moves that could be made.
This experimental scenario corresponds to the completion of the game concerning the positions that the tokens can take. Table 5 describes the scores for the positions of both the arrays and the matrix. Note that the scores are different for each player depending on the ending position of the tokens, so that each player's score is based on the final position he/she occupies in the DS index.
Table 5 Final position of the tokens in the DS.
| Structure | Column number | Subindex | Score player 1 | Score player 2 |
|---|---|---|---|---|
| Array1 | 0 | 0,1,2...11 | 5 | 0 |
| Array2 | 0 | 0,1,2...11 | 0 | 5 |
| Matrix | 0 | (0,0), (0,1)...(0,5) | 0 | 5 |
| Matrix | 1 | (1,0), (1,1)...(1,5) | 0 | 3 |
| Matrix | 2 | (2,0), (2,1)...(2,5) | 0 | 2 |
| Matrix | 3 | (3,0), (3,1)...(3,5) | 0 | 1 |
| Matrix | 4 | (4,0), (4,1)...(4,5) | 1 | 0 |
| Matrix | 5 | (5,0), (5,1)...(5,5) | 2 | 0 |
| Matrix | 6 | (6,0), (6,1)...(6,5) | 3 | 0 |
| Matrix | 7 | (7,0), (7,1)...(7,5) | 5 | 0 |
If the player or the machine wants to play a second turn, they must plan a move that allows them to reach an empty column in the second turn. This move is particularly important because it means making four consecutive advances if the player executes the moves in an optimal way. A move where a second turn is obtained from a second advance corresponding to the player's first turn. The counters marked with the green circle correspond to the first advance of the turn, which show that in the second advance the player has the right to move one column forward. Therefore, the piece with subscript 0,1 marked in orange is moved to column 2, which is empty at that moment. This move will allow the player to have one more turn, thus maximizing the gain.
To validate the game, some tests that allowed us to check the execution times in games developed with the AI and real users were conducted. Initially, games with three real users were developed; all the users faced each other during two games, the results of the games by time in minutes and seconds are described in Table 6.
Table 6 Player vs Player starting times.
| Player 1 | Player 2 | Player 3 | |
| Player 1 | - | 11m:14s | 12m:19s |
| Player 2 | 11m:47s | - | 12m:44s |
| Player 3 | 11m:55s | 10m:51s | - |
The loading time of the application is 8 seconds, the execution of the online games depends directly on the match making and the connection stability of the players. For online games, it is possible to create unlimited games with a maximum of two players each, that is, 1 real player vs 1 real player. If it is a local game, the maximum number of users is two players depending on playing with the AI or with another player.
Table 7 shows the game times of each game in seconds. It can be seen that player 3 (red) was the one who spent most time in his games, while player 2 (red) was the one who spent less time. Player 3 played the fastest game (blue) vs. player 2 (red), while the slowest game was played by player 3 (red) vs. player 2 (blue). According to these results, there is no significant correlation between the games, since they vary in time according to the movement decisions of the players.
The movements of the machine are executed with a speed of 2.5 seconds while the animation of the scroll card is performed in the application. On average, the AI vs AI game lasts three minutes, although the games between an AI and real users generally depend on the time the human spends to execute the movement, so it will be longer than AI vs AI. Table 7 shows the times of a game played by three real users with each of the three AIs. It is evident that the game between a player and Alex AI lasts 9 minutes approximately; Drake AI, 7 minutes approximately; and Kira AI, 6 minutes approximately. It should be noted that time is not constant in the games since the human player varies his movement time while the machine makes its choice immediately after the user makes the last movement.
Table 7 Player vs Player starting times.
| Player 1 | Player 2 | Player 3 | |
| Alex AI | 9m:16s | 9m:52s | 8m:56s |
| Drake AI | 7m:11s | 6m:14s | 6m:49s |
| Kira AI | 4m:58s | 5m:34s | 5m:54s |
Figure 11a shows the game times of the machine with real players in seconds. It shows that Kira AI was the one who spent less time in her games. Since the AI tends to move pieces in advance, it is possible that the user takes advantage of the AI movements to play in an optimal way and end the game, or that the AI executes optimal movements according to the opponent's way of playing. In the case of Alex AI, it spent the most time in games, it tends to move the pieces in the back, so the pieces tend to concentrate at the center of the game board according to the opponent's movements, which are generally balanced. Finally, Drake is in the middle, since it is a balanced AI, which causes the pieces on the board to disperse during the first minutes so there is fluidity in the game by the two players. As for real players, they do not reflect a specific behavioural trend over time, on the contrary, they adapt to the AI's way of playing when executing movements.
In the previous scenarios it became evident that the Minimax application must comply with the playing rules by executing valid and optimal moves, so that it can compete against a real player, learn from their moves, and then use them to continue developing the game.
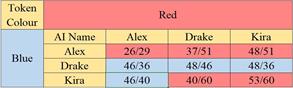
Figure 11b shows the scores obtained after playing with the AI. The table shows the matches where each AI has played with itself and two opponents. In each game the red piece had the first turn. In general, from data observation, it is inferred that Drake won the games over his opponents, except when he played with himself. On his side, Alex lost all the games, except the one he played with himself, when red pieces won. Finally, Kira won both games to Alex but she lost two games against Drake; when she played with herself, red pieces won. In the following figures the final score of each player is stored. The boxes show the results with the distribution of points obtained in the game by player separated by a slash, to identify the winner of the game in the table, the cells have a colour depending on the axis where the player who obtained more points is located. So, if the winner was an AI of the vertical axis the cell will be blue. Hence, if there is a winner in the horizontal axis, the cell will be red. For example, Alex located on the vertical axis plays with Drake on the horizontal axis, they obtain a score of 37/51 and the box is red, it means that the winner is Drake with 51 points versus Alex with 37 points.
As of the first iteration above you have several AI opponents. In the second iteration, games will be played again to check if the scores are maintained or new atypical events occur in order to consider them in the difficulty criteria of each AI. Next, more games will be played to find new scores and the same players will be kept with their respective ways of playing.
After the second iteration, the same pattern of victories as the first iteration is maintained, so it is necessary to conduct another one to find diverse ways of ending the games played by the AI. It should be noted that between two virtual players the result is always the same because they choose the same movements. In Figure 11c, after completing the third iteration, results are different from to the two previous iterations, although the difference in points is almost the same in all matches. These results allow us to conclude that there is no uniformity when playing with the AI, random and completely different values can be found because there are more decisions to be made and a real user will never play the same game with AI.
IV. CONCLUSIONS AND FUTURE WORK
After completing the project, the rules and mechanics of the Linja game were implemented in a software for its subsequent use as a game. The Minimax algorithm was applied to make it an intelligent system where both human and machine opponents could play the game and find a winner.
The project had limitations such as the complexity of controlling all possible moves; since Linja is a game with multiple possibilities, adapting them to find the right and most intelligent move was the biggest problem when programming. It was necessary to use libraries and add-ons that facilitated the development of the game.
Undoubtedly throughout the project, it was noticeable that improvements in the graphical interfaces are very important to achieve an intuitive system and for all movements to be clear to users, so it was necessary to support the development of the project with tools that facilitated the correct application of components to create an intuitive and functional GUI.
The future work, considering everything we learned in this project, is based on improving the graphics and making it adaptable to other operating systems such as Android. Also, make it possible to access the game via Internet to play online with other real opponents and with the AI’s difficulty levels using and applying distributed systems.