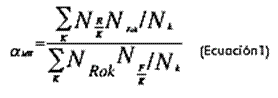Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introducción
Alrededor de 180.000 jóvenes chilenos (43 % de la matrícula secundaria nacional) de los deciles de ingreso más bajos cursan la Educación Media Técnica (EMTP) (Ministerio de Educación -Mineduc-, 2013; Sevilla, 2012; Ortiz, 2011). De estos jóvenes, solo un 38 % continúan sus estudios cursando primer año en la Educación Superior Técnico Profesional (ESTP), lo cual es una tasa baja, si se considera que la tasa neta de participación nacional en educación superior es 70,7 % (Rucci et al., 2015). Un menor número de estudiantes de EMTP ingresan a la educación superior universitaria, algunos gracias a los beneficios económicos del estado como becas y créditos y luego de postergar su ingreso por un tiempo considerable (hasta 5 años después).
Los estudiantes de la EMTP deberían poder participar en condiciones de igualdad con aquellos estudiantes que reciben mayor tiempo de formación general (quienes reciben un currículo científico humanista más intensivo) y con aquellos cuyas condiciones socioeconómicas (mayor capital económico y cultural) les permiten el acceso expedito a las universidades de mejor calidad (Leyton et al., 2012). Esto es un tema de justicia educacional que se ha discutido previamente en debates sobre el carácter reproductor de la desigualdad que puede implicar la existencia del sistema formativo diferenciado por modalidades de estudios técnicos o humanistas (Farías y Carrasco, 2012; Larrañaga et al., 2013; Orellana, 2011).
La educación técnico profesional (TP) es importante para el desarrollo de las naciones (Organización para la Cooperación y el Desarrollo Económico -OCDE-, 2009; 2017). La mayoría de los países de la OCDE tienen un recurso humano altamente preparado en el nivel técnico profesional y menos concentrado en el nivel profesional (Meller y Rappaport, 2008). En el contexto chileno, los padres de familia y los mismos estudiantes de EMTP tienen aspiraciones y deseos de trayectorias educativas que los conduzcan a un nivel educativo más avanzado como el universitario (Sepúlveda y Valdebenito, 2014; Sepúlveda, 2016). Dicho nivel es más valorado socialmente y en algunos casos representa un mayor retorno económico a la inversión por la inserción laboral y los salarios que implica (Carrasco y Venables, 2010; Secretaría Ejecutiva de Formación Técnico-Profesional, 2010; Mineduc, 2018a, 2018b) y no implica las dificultades que se han observado en el nivel de formación técnico superior -escaso financiamiento público, débil vinculación con el sector productivo, carencia de mecanismos de articulación y movilidad- (Bernasconi, 2006; Donoso et al., 2012; Gaete y Morales, 2011).
Los estudiantes del nivel EMTP buscan desarrollar una trayectoria que los conecte pronto con el mundo del trabajo, pero sin dejar de lado la posibilidad de una formación universitaria en el futuro (Sepúlveda y Valdebenito, 2014; Sepúlveda, 2016; Farías y Carrasco, 2012; Farías y Sevilla, 2012). En este sentido, es importante analizar las posibilidades que tienen los estudiantes chilenos de EMTP de que en su trayectoria educativa puedan ingresar a un establecimiento educativo de nivel superior y que sea selectivo como es el caso de las Universidades del Concejo de Rectores (CRUCH) y sus adscritas, cuyo acceso está condicionado a los resultados en la PSU. Este acceso se ve obstaculizado debido a las dificultades en el rendimiento académico que podría producir la formación bajo un currículo de educación diferenciada (Farías y Carrasco, 2012).
Evidencia preliminar señala que en la prueba estandarizada de ingreso a la universidad (PSU) se presentan diferencias de desempeño entre grupos que pueden afectar los resultados de los estudiantes de media técnica para el acceso a la educación superior (Mineduc, 2020; Centro de Estudios Mineduc, 2019).
Aunque los principios del nuevo Sistema Único de Admisión de la Educación Superior son claros y socialmente deseables, la nueva legislación deja abierta la pregunta sobre cuáles deben ser las características de un sistema de admisión de estudiantes vulnerables a la ESTP. Una de estas características de base y altamente deseables es que se promueva la redistribución y el reconocimiento, y que el sistema de admisión permita una selección virtuosa. Sevilla (2015) define la selección virtuosa como una en la que no se discrimine por el nivel socioeconómico, se prediga la probabilidad de éxito en la educación superior (egreso oportuno y desempeño) y se permita discernir aspectos psicológicos que favorezcan la retención.
El presente estudio se enfoca en el desempeño en la PSU condicional a la modalidad de estudios (técnico profesional vs. académica). Según el reporte del Departamento de Evaluación, Medición y Registro Educacional (DEMRE, 2018), la distribución de respuestas correctas a los ítems de la prueba PSU en el año 2018 para el total nacional es en promedio 37 preguntas correctas para lenguaje (51 % del total de la prueba), 25 preguntas en matemáticas (33 %), 31 preguntas en historia, geografía y ciencias sociales (41 %), 30 preguntas en ciencias (38 %). Es importante analizar qué ocurre en el sector de matemáticas que presenta el resultado más bajo, para los técnicos de media, tema que se abordará en el presente estudio.
El informe de Pearson Education (2013) sobre evaluación de aspectos técnicos de la prueba PSU sugirió considerar
el funcionamiento diferencial de los ítems del pilotaje y los de operación (sesgo); la falta de comparabilidad "equating" entre las formas aplicadas en diferentes años; y el mayor énfasis de la prueba sobre la modalidad científico-humanista (CH) que sobre la modalidad técnico-profesional (TP). (Contraparte Técnica CRUCH-Mineduc, 2013).
Entre las recomendaciones del estudio Pearson en el año 2013 (citado por Contraparte Técnica CRUCH-Mineduc, 2013) se sugirió considerar los resultados DIF o del funcionamiento diferencial de los ítems por grupos (como el tipo de establecimiento, la modalidad, el género, etc.) del piloto como parte de los criterios de selección de ítems para las formas operacionales de la prueba. También se sugirió utilizar en los análisis dif otras variables relevantes tales como la modalidad de enseñanza (TP vs. CH) y el nivel socioeconómico.
A 7 años de la implementación del informe de Pearson (Pearson Education, 2013; Mineduc, 2016) cabe preguntar si las recomendaciones del informe se han implementado, en especial aquellas sobre el funcionamiento diferencial de los ítems, ya que, si el sesgo persiste en la elaboración de la PSU, se afectarían las posibilidades de los egresados de la formación TP (técnico profesional de media o superior) para el acceso a las universidades del Sistema Único de Selección. Así mismo, se restringirían los beneficios estudiantiles que este acceso conlleva (becas y créditos).
El presente estudio busca establecer si los ítems de la PSU de matemáticas empleados en la admisión para el año 2018 presentan DIF. El grupo focal (grupo minoritario) son los estudiantes de modalidad técnico profesional y el grupo mayoritario, los estudiantes de la media académica. La hipótesis que orienta el estudio es que en los ítems de la PSU de la admisión para el año 2018 hay un funcionamiento diferencial (DIF) en particular en el área de matemáticas, que puede ser condicional a aspectos como la modalidad de estudios (científico humanista o técnico profesional). Este funcionamiento diferencial de los ítems de la PSU se podría asociar con las puntuaciones más bajas que reciben los estudiantes de la modalidad técnica EMTP, y que impactan sus oportunidades de acceso a la educación superior universitaria en Chile (Mountjoy, 2019).
Metodología
Participantes
Para la selección universitaria del año 2018, aproximadamente 295 531 estudiantes se inscribieron para la PSU y 262 139 (89 %) rindieron las pruebas de los sectores de lenguaje y matemáticas (DEMRE, 2018). De entre estos estudiantes, casi 90 000 pertenecían a la modalidad diferenciada o técnica (EMTP). En el presente estudio, se emplearon los datos de los estudiantes que respondieron las 4 formas de la prueba de matemáticas (n = 124 750 estudiantes) distribuidos como aparece en la tabla 1. Siguiendo las recomendaciones de Herrera et al. (2005), para la detección de sesgo en los ítems y de su funcionamiento diferencial (DIF) mediante análisis de tablas con el estadístico de Mantel-Haenszel (MH), se empleó un tamaño de muestras apropiado para el análisis (ver tabla 1). Esto ya que, según los autores, 500 examinados en el grupo de referencia y 100 en el focal producen baja detección; mientras que el DIF no uniforme (cuando hay interacción entre nivel de aptitud y pertenencia a un grupo), se puede detectar usando grupos iguales de 1500 examinados o más.
Instrumento
La PSU mide habilidades cognitivas y contenidos que el estudiante aprende a partir del Marco Curricular para la Educación Básica y Media de 1998, reorientado en el 2009 (Mineduc, 2009). Este marco contiene los "Contenidos mínimos obligatorios" (conocimientos específicos) y los "Objetivos fundamentales" (competencias) del aprendizaje que se evalúan con las subpruebas de la PSU desde el proceso de admisión de 2004. Concretamente, se evalúa lenguaje y comunicación, matemática, historia, geografía y ciencias sociales y ciencias (área que se compone de un módulo común y de módulos electivos de biología, física, química y un módulo técnico profesional). La PSU emplea ítems de selección múltiple con cinco opciones de respuesta. Cada ítem corresponde a un contenido mínimo y unas habilidades cognitivas específicas.
La PSU es una prueba estandarizada referida a norma y que otorga un puntaje ponderado único empleado para tomar decisiones de admisión a universidades selectivas (adscritas al Sistema Único de Admisión -SUA-). La prueba tiene varias formas o formularios con ítems parecidos en contenido y características que se hacen equivalentes por medio de un procedimiento de "equating" o anclaje de puntajes, el cual se implementó después de las sugerencias del reporte Pearson del año 2013. Estos ítems se pueden puntuar de forma equivalente por medio de un proceso de alineamiento "linking" que atenúa las diferencias de puntaje entre las formas (DEMRE, 2016).
En general, la PSU evalúa: lenguaje y comunicación, que incluye 80 ítems de evaluación indirecta de la escritura y de contenidos de lectura; matemática, con 80 ítems sobre números, álgebra, geometría, datos y azar; historia, geografía y ciencias sociales, con 80 ítems que abarcan espacio geográfico, perspectiva histórica chilena y mundial, democracia y desarrollo; ciencia, con 54 ítems, 18 de cada subsector: biología, física y química de I y II medio y una subprueba electiva a partir de III medio, que incluye 2 de las 3 disciplinas con un total de 26 ítems cada una. Además, el área de ciencias contiene un módulo exclusivo para estudiantes de la rama técnico profesional (26 ítems que incluyen 10 de biología, 8 de física y 8 de química). Cada prueba evalúa contenidos y habilidades cognitivas de acuerdo con las categorías cognitivas de Bloom, sin embargo, el módulo EMTP se enfoca en habilidades cognitivas de menor complejidad, como reconocimiento y comprensión, y no aborda habilidades más complejas como aplicación, análisis, síntesis y evaluación (DEMRE, 2016).
Procedimiento
Tabla 1 Tamaño de las muestras analizadas
| Grupo de referencia (estudiantes científico humanistas) | Grupo focal (estudiantes técnicos) | |
|---|---|---|
| Forma 111 | 32 926 | 11 517 |
| Forma 112 | 12 083 | 5 373 |
| Forma 113 | 29 955 | 10 379 |
| Forma 114 | 15 229 | 7 288 |
Detección del sesgo. Método estadístico para abordarlo. Según Cuevas (2013), entre otros autores, un ítem presenta DIF cuando la probabilidad de responderlo correctamente no depende solo del nivel de habilidad de la persona en el rasgo medido por la prueba, sino también de otras variables, lo que infringe el supuesto de invarianza de medida: "Es decir, si evaluados comparables en la puntuación total en una prueba, pero de diferentes grupos, responden de diferente forma a los ítems individuales hay DIF o sesgo potencial" (Cuevas, 2013, p. 22). Esto significa que el DIF está condicionado a variables diferentes a la habilidad que son variables irrelevantes para los propósitos de la prueba, pero que afectan el desempeño. Algunos ejemplos de estas variables pueden ser el "momento de administración de la prueba, sexo de los estudiantes, currículo del alumno o 'idioma de aplicación' entre otros" (Elosua, 2006, p. 248).
Las diferencias en habilidad no constituyen sesgos o DIF, por lo cual la medida de diferencia en habilidad se llama "impacto". Pueden coexistir DIF en presencia de diferencias en la habilidad de los respondientes, por ejemplo, cuando los ítems están redactados usando palabras que no son comprensibles en un contexto cultural o que reflejen unos valores que son contrarios a los del grupo cultural de los examinados, lo cual afecta su desempeño.
Sin embargo, no siempre que se presentan diferencias sustantivas entre los grupos habrá DIF:
El solo hecho de que un instrumento de medida arroje resultados sistemáticamente inferiores para un grupo en comparación con otro no constituye evidencia de sesgo, ya que si efectivamente existen diferencias entre los grupos en lo que la prueba mide es apenas de esperarse que sus resultados las muestren. Estas diferencias se conocen en el lenguaje técnico como impacto o diferencias válidas. (Herrera et al., 2005, p. 51)
Existen diferentes métodos para estimar si existe o no DIF en los ítems. Los métodos más usados para establecer el funcionamiento diferencial de los ítems de una prueba son el estadístico X 2 Mantel-Haenszel (MH) y la diferencia de la dificultad o diferencia del parámetro "b" (dificultad).
El X 2 MH es un método con base en tablas de contingencia y básicamente consiste en detectar si las diferencias entre quienes responden y no responden correctamente se mantienen iguales entre los grupos focal (minoritario) y de referencia (mayoritario) en los diferentes niveles de habilidad. Por otra parte, el procedimiento de la diferencia de la dificultad se basa en la existencia de esta para los grupos considerando el nivel de habilidad. El MH (Elosua, 2006; Kamata y Vaughn, 2004) se estima como odds ratio según la ecuación 1.
El estadístico MH representa la razón de quienes aciertan en el grupo de referencia
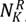, multiplicado por la razón de quienes fallan en el focal
, dividida entre la razón de quienes fallan en el grupo de referencia
multiplicada por la proporción de quienes aciertan en el focal
El MH evalúa la igualdad en las proporciones entre quienes contestan correctamente y quienes no lo hacen. Hace uso del estadístico X 2 de MH que es una distribución con n-k grados de libertad, siendo n el número de estratos (particiones del puntaje total en la prueba) y k el número de grupos (focal y de referencia).
Por otra parte, la prueba de diferencias de dificultad se enfoca en el parámetro (b) del ítem para los dos grupos (focal y de referencia). Su cálculo se limita a la estimación de la diferencia entre las dificultades para los grupos.
En el presente estudio se desarrollaron los análisis DIF con varias muestras de estudiantes usando como grupo focal (minoritario) a los estudiantes de media de la modalidad técnico profesional. A su vez, el grupo de referencia se compuso de los estudiantes de modalidad CH (académica o científico humanista).
El análisis se hizo de forma separada para las 4 formas equivalentes de la prueba para el área de matemáticas, cada una con 80 ítems, que pueden repetirse en diferentes formas. La suma total de los ítems de las 4 formas equivale a 180 ítems. Con las estimaciones de dif se estableció cuáles ítems tienen potencial sesgo.
Para la detección del DIF se calculó el estadístico MH ( X 2 de Mantel Haenszel, MH). Se empleó el software R para establecer la diferencia en los parámetros de dificultad y pseudoazar y se usó el software DIFAS 5.0 para el análisis de MH. Para determinar que un ítem tiene DIF se usaron criterios como que el MH fuera significativo estadísticamente. También se tuvo en cuenta los valores log-odds de MH y MH-Z (log-odds estandarizado).
Representación gráfica de los parámetros de los ítems. Para determinar las diferencias entre grupos (CH vs. TP) se calcularon los parámetros de dificultad y pseudoazar y se procedió a hacer una representación gráfica de las diferencias entre los grupos en los parámetros calculados. Todos los ítems (ítems = 180) se representan en un mismo gráfico y no en curvas de información separadas. Los puntos de la gráfica representan el valor del parámetro para un ítem en particular y todos los puntos se ajustan a una recta. Esta representación gráfica se hizo por medio del programa R.
Identificación por subpruebas de los ítems que tienen sesgo contra los estudiantes técnicos. Finalmente, y debido a que no se cuenta con los ítems para realizar el análisis de contenido de aquellos, se presenta una propuesta alternativa para establecer qué temáticas del currículo evaluadas por la PSU se dificultan más a los estudiantes de media técnica. Se estableció cuáles son las subpruebas de matemáticas (álgebra, geometría, números y probabilidad) cuyos ítems presentan mayor dificultad y afectan a los estudiantes técnicos, por medio de una representación gráfica. En esta representación por subpruebas, los ítems se agrupan por áreas de contenido, y se presentan las diferencias en el parámetro de dificultad entre los estudiantes científico-humanistas y los estudiantes técnicos. El parámetro de dificultad que se representa gráficamente (figura 3) fue obtenido con el modelo 1PL(modelo de Rasch), que incluye solo el parámetro de dificultad. Por su parte, las gráficas 1 y 2 se desarrollaron con los modelos 2PL y 3PL.
Resultados
Detección del sesgo. Los resultados de la detección del sesgo en los ítems se presentan en la tabla 2.
Tabla 2 Detección del sesgo en los ítems de las 4 formas de la prueba PSU de matemáticas
| Forma | Total de ítems | MH LOR & LOR Z | CDR (combined decision rule) | ETS | |
|---|---|---|---|---|---|
| Núm. de ítems a favor del grupo mayoritario | Núm. de ítems a favor del grupo minoritario | Total de ítems que presentan sesgo | |||
| Forma 111 | 80 | 19 (23,7 %) | 21 (26,2 %) | 36 (45 %) | A |
| Forma 112 | 80 | 14 (17,5 %) | 13 (16,2 %) | 23 (28,7 %) | A |
| Forma 113 | 80 | 17 (21,2 %) | 18 (22,5 %) | 33 (41,2 %) | A |
| Forma 114 | 80 | 12 (15 %) | 12 (15 %) | 27 (33,7 %) | A |
El MH LOR es el valor log-odds del estadístico MH (Mantel Haenszel). Este se interpreta considerando que los valores positivos corresponden a sesgo a favor del grupo de referencia, los valores negativos a favor del grupo focal (Penfield, 2013). Sin embargo, este criterio no indica que grupo se favorece cuando hay sesgo en el ítem. Por este motivo, se usa la regla complementaria de LOR Z (valor estandarizado del log-odss del estadístico MH). Si este es mayor a 2.0, el sesgo favorece al grupo mayoritario (estudiantes CH), si es menor de 2.0, entonces favorece al grupo minoritario (Penfield, 2013). La CDR (combined decision rule) indica que existen ítems con sesgo o DIF no uniforme. El número total de los ítems con sesgo puede diferir de acuerdo con el uso de las reglas de decisión, por ejemplo, pueden reportarse algunos ítems de más con DIF si se sigue la regla CDR.
Los resultados de la tabla 2 indican que hay un funcionamiento diferencial en todas las formas de la prueba de matemáticas de la PSU y que este funcionamiento favorece a ambos grupos (estudiantes técnicos TP y estudiantes humanistas CH). Sin embargo, este sesgo es de categoría "A", lo cual significa que el estadístico de MH no es significativo al nivel de 0.05. Este nivel de sesgo es mínimo de acuerdo con las reglas de valoración del DIF de ETS -Educational Testing Service- (Zwick, 2012). Las formas tienen al menos un 15 % de ítems con DIF que favorece a cada uno de los grupos. La forma 111 muestra el nivel más alto de DIF (45 %). No se presentan ítems con sesgo crítico o categoría C, que son los que por regla general son suprimidos.
Representación gráfica de los parámetros de los ítems. Después de calcular los parámetros con los modelos de 2PL (que incluye la discriminación y la dificultad) y 3PL (que incluye todos los parámetros) se procedió a representar gráficamente las diferencias entre grupos en los parámetros de dificultad y pseudoazar. Esta representación incluye a todos los ítems de la prueba de matemáticas de la PSU (ítems = 180). En la figura 1, se representa la diferencia en los parámetros entre grupos CH (estudiantes humanistas) y TP (técnicos).
Figura 1 Representación gráfica. El parámetro de pseudoazar se presenta en el panel izquierdo. El parámetro de Dificultad se representa en el panel derecho. Modelo 3 PL
En la figura 1 se representan las diferencias entre grupos en los parámetros calculados con el modelo 3PL. En el panel izquierdo se observa que el pseudo-azar es mayor para los estudiantes técnicos TP (los puntos que representan la diferencia entre grupos por ítem se encuentran sobre la recta de ajuste). En el segundo panel se observa que la dificultad también es mayor para el caso de los estudiantes TP ya que la diferencia aritmética entre grupos en el parámetro por cada ítem se representa con puntos por encima de la recta de ajuste, lo que muestra que la diferencia favorece a los estudiantes de la media académica y afecta al grupo de estudiantes técnico profesionales.
Del total de los ítems analizados (180), aquellos que favorecen a los estudiantes de tp tienen parámetros de pseudo-azar más grandes que los ítems que favorecen a los estudiantes CH (68,64 % de los 180n ítems). Pero, en su mayoría (97,04 % del total de 180 ítems analizados), desfavorecen a los estudiantes TP ya que tienen parámetros de dificultad más grandes. Esto significa que, aunque el índice de pseudo-azar es más alto para los ítems respondidos por estudiantes TP, la diferencia en los parámetros de dificultad es más acentuada. Esto puede ser indicativo de que los estudiantes técnicos profesionales (TP) requieren mayor esfuerzo para lograr incrementar sus probabilidades de responder correctamente en los ítems de matemáticas de la PSU y no se trata de que hagan adivinación de la respuesta.
La figura 2 confirma los resultados obtenidos con el modelo de 3 parámetros. En esta representación de los parámetros calculados a partir de un modelo 2PL, se encuentra que los ítems con funcionamiento diferencial que favorecen a los estudiantes TP tienen parámetros de pseudoazar más grandes que los ítems de CH (81,65 %) y tienen parámetros de dificultad más grandes que los ítems que favorecen a los estudiantes CH (97,63 %).
Figura 2 Representación gráfica de la diferencia en los parámetros entre grupos CH (estudiantes modalidad humanista) y tp (modalidad técnica). Modelo 2PL
Identificación por subpruebas de los ítems que tienen sesgo para los estudiantes técnicos. Para identificar el contenido matemático que se evalúa y que tiene un mayor nivel de dificultad para los estudiantes de la modalidad técnico profesional se desarrolló una representación gráfica adicional. En esta, se identifican las diferencias en el parámetro de dificultad entre los grupos (científico humanista vs. técnico profesional) por subprueba de matemáticas (álgebra, geometría, números y probabilidad) con su respectivo intervalo de credibilidad. Si la diferencia entre grupos por cada ítem es cercana a 0, el ítem no tiene funcionamiento diferencial (no afectará a ninguno de los grupos) y estará representado cerca de la línea de ajuste en la figura 3. La figura 3 presenta estas diferencias en la dificultad entre grupos científico humanista vs. técnico profesional.
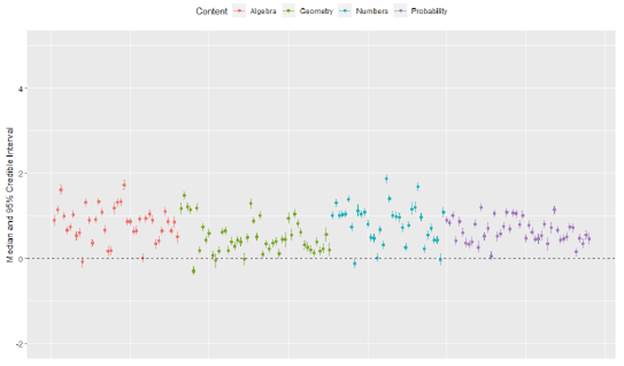
Figura 3 Representación gráfica de la diferencia por subprueba en el parámetro de dificultad entre grupos CH (estudiantes humanistas) y TP (técnicos). Modelo 1 PL
Nota: Cada punto representa la diferencia aritmética entre grupos (TP vs. CH) del parámetro de dificultad por ítem, representando el total de 180 ítems. En rojo los ítems de la subprueba de álgebra, en verde los de geometría, en azul los ítems de números y aritmética, en morado probabilidad y estadística.
La figura 3 muestra que la dificultad es mayor para el grupo tp en 97 % del total de los ítems (180 ítems de 4 formas diferentes), y solo pocos ítems presentan una diferencia en la dificultad equivalente a 0 (que se acercan a la línea de ajuste). Esto implica que se debe profundizar en las causas de estas diferencias en el nivel de dificultad de los ítems presentados al grupo técnico profesional. Se sugiere por tanto la revisión conceptual y de diseño de los ítems que están representando estas barreras para los estudiantes tp.
Conclusiones
El presente estudio aporta evidencia que favorece la hipótesis de que en los ítems de la PSU subprueba de matemáticas persiste un funcionamiento diferencial (DIF) en los ítems del sector de matemáticas, que no se debe a la habilidad de los estudiantes en las pruebas (rasgo latente), sino que puede ser condicional a aspectos como la modalidad de estudios (científico humanista o técnico profesional). Este funcionamiento diferencial, o sesgo, existe en al menos 20 % de los ítems de matemática (medido con el estadístico de MH) en cada una de las formas (ver tabla 1), lo cual dificulta el desempeño de los estudiantes TP en la PSU.
Aunque este sesgo es mínimo, y también hay sesgo que favorece al grupo de los estudiantes de la media científico humanista, el sesgo se observa de forma transversal en todas y cada una de las formas de la prueba de matemática. Por tanto, se requiere profundizar en las causas de este funcionamiento diferencial, y hacer su respectiva corrección, incluso desde el pilotaje de la prueba. Una forma es indagando con estudiantes de la media técnica sobre los aspectos que dificultan su desempeño en los ítems de la PSU. Cuevas (2013) maneja una aproximación cualitativa para comprender estas dificultades en el caso de estudiantes de etnia indígena que responden a la prueba estandarizada de Colombia, Saber 11 (equivalente en propósito a la PSU de Chile).
El presente estudio permite establecer que pasados 8 años de la consultoría de Pearson (2013) para evaluar la PSU, se requiere implementar más correctivos desde el pilotaje de la prueba y se deben eliminar todos los ítems que presenten funcionamiento diferencial, incluso en el caso de que este sea de la categoría más baja o categoría "A", según la clasificación de ETS, ya que esta categoría no representa ausencia de sesgo, sino falta de significancia estadística del MH.
En cuanto al abordaje metodológico, el presente estudio recurrió al estadístico X 2 de MH. Las mejores prácticas en detección de sesgo de la ETS (Zwick, 2012) sugieren que se debe considerar la significancia estadística del MH, pero como se presentó en este estudio, este criterio por sí solo no es suficiente. Se requirió revisar los valores log odds (MH LOR) y log-odds estandarizado (MH LOR Z) del estadístico de Mantel Haenszel para poder tener una regla de decisión sobre el sesgo y a qué grupo favorecía. Por otra parte, el CDR, que se basa en el estadístico X 2 de Breslow-Day, permite establecer un mayor número de ítems que presentan sesgo. Es necesario que se esclarezca en la literatura psicométrica la regla de decisión apropiada (Penfield, 201 3), o que se proceda como el presente estudio, en el que se validó la concurrencia de varios indicadores estadísticos y representaciones gráficas.
Por otra parte, la representación gráfica de los parámetros permite ver las diferencias entre grupos respecto a parámetros que por lo general se observan agregados en la gráfica de la curva de información del ítem (CII). La CII es una representación gráfica que no permite determinar las diferencias que desfavorecen a los estudiantes TP (media técnica profesional) comparado con los estudiantes CH (humanistas) de manera visual. La representación gráfica presentada en este estudio es una aproximación que permite ver estas diferencias, pero se restringe a los parámetros de dificultad y pseudoazar, ya que no se emplea la discriminación por no aportar información adicional sobre la comparación de los grupos.
El estudio encontró que los ítems de la PSU de matemáticas presentan mayor dificultad y pseudoazar que desfavorece a los estudiantes técnicos. Es importante considerar estas diferencias, ya que limitarse a los resultados del sesgo que arroja el estadístico MH puede subestimar las dificultades que afrontan los estudiantes técnicos al responder la PSU de matemáticas. Por ejemplo, el análisis del presente estudio sobre el desempeño en las subpruebas de matemáticas (álgebra, geometría, números y probabilidad) indica que hay dificultad de los ítems en al menos 97 % de los ítems mientras que el estadístico de MH supone que solo 20 % de los ítems presenta sesgo que afecta al grupo minoritario.
Por tanto, ya que estos estudiantes técnicos desconocen el material evaluado por la PSU de matemáticas (debido a una insuficiente formación general de matemáticas de media) y además responden al azar, y como se estableció en el presente artículo los ítems presentan sesgo que tampoco les facilita responder de forma correcta a estas preguntas.
Los ítems en sí se facilitan para estudiantes de la media académica o científico humanista. Previamente la PSU incluía en su diseño ítems de ciencias, especiales para el grupo técnico profesional, pero esta adaptación no se extendía al área de matemáticas (DEMRE, 2016).
Una posibilidad para estudios futuros es mejorar la detección de las diferencias de los parámetros en los ítems por medio del uso del modelo de estadística bayesianas. Esto es pasar de una aproximación frecuentista y cambiar a una aproximación probabilística. En el caso bayesiano, la aproximación probabilística implica que los parámetros pueden estimarse en términos de intervalos de credibilidad, en los que el valor del parámetro puede tomar un rango de valores. Esto puede cambiar un poco la representación gráfica y las probabilidades de que más parámetros se encuentren sobre o por debajo de la recta que ajusta los puntos en la representación gráfica. Esto implicaría un acercamiento más exacto a determinar qué ítems favorecen o no a los estudiantes técnicos que presentan la PSU.
Igualmente se sugiere que los estudios futuros hagan análisis de contenido de los ítems que presentaron comportamiento diferencial, con el objetivo de confirmar si se presenta el sesgo que el presente estudio ha detectado por medios estadísticos. Por ejemplo, este análisis de contenidos permitirá determinar si el sesgo es producto de los procesos de enseñanza y aprendizaje, del currículo diferenciado o si se refiere a la forma como se evalúa el contenido. Esto permitiría analizar si lo que se evalúa es pertinente a la luz de la investigación en matemática educativa o refleja problemáticas reportadas en dichas investigaciones para el caso de los estudiantes tp que solo reciben el currículo general hasta el nivel de segundo de media, considerando que los estudiantes ch sí lo reciben hasta cuarto de media.
En el contexto actual, la PSU es transformada y se denomina Prueba de Admisión Transitoria a la Educación Superior 2020-2021 (DEMRE, 2020). Esta nueva prueba desarrollada por el DEMRE busca mejorar la equidad y evaluar los contenidos priorizados en el área curricular de matemáticas, como consecuencia de la pandemia de coronavirus. Asimismo, busca mejorar el acceso de los estudiantes de media a la educación superior, ya que se centra en habilidades más avanzadas y necesarias para la educación universitaria, como resolver problemas, representar, modelar, argumentar, y da menos énfasis a la amplitud de contenidos de los currículos.
Análisis futuros de sesgo condicional a la modalidad de estudios, sobre los ítems de la nueva prueba de transición, como el desarrollado en el presente artículo, permitirán establecer si se sigue afectando el nivel de respuesta de los estudiantes de media técnica, debido a los ítems y su potencial sesgo.
