Introducción
El aprendizaje colaborativo (AC), el aprendizaje activo (AA), las tecnologías de la información y la comunicación (TIC) y el aprendizaje basado en juegos (ABJ) son estrategias que tienen gran impacto en el aula, como se indica en Troussas y Virvou (2020) : “El AC asistido por computadora se ocupa de la interacción entre los alumnos para trabajar en grupos y cómo la colaboración y la tecnología facilitan el intercambio y la distribución de conocimientos entre ellos”. Además, se ha demostrado que el AA mejora el rendimiento de los estudiantes y debería ser más constante su uso en el aula, ya que es una actividad en la que se construye conocimiento y comprensión de las temáticas (Brame, 2019). Asimismo, el ABJ aporta a la práctica educativa y a su vez en la ampliación del conocimiento y las habilidades (König et al., 2020). Cabe anotar que la aplicación de incentivos en el aula ha tenido un resultado significativo en la motivación de los estudiantes al aprendizaje (Rahimi et al., 2021).
En el ámbito de las matemáticas, conviene destacar que el cálculo es una de las asignaturas más importantes en el estudio de las ingenierías, por sus aplicaciones reales en el desarrollo de modelos matemáticos enfocados en la sencillez y la precisión (Larson y Edwards, 2016). El cálculo combina elementos de las matemáticas como el álgebra y la geometría; ejemplo de ello es el proceso de derivación de una función en el que existen cuatro etapas fundamentales: la función original, reescribir, derivar y simplificar; del mismo modo, el proceso de integración indefinida coincide con la derivación en las etapas de reescribir y simplificar, siendo la integral original y el proceso de integrar las etapas restantes (Larson y Edwards, 2016).
El poco interés y desmotivación de estudiantes de ingeniería son una problemática identificada en la enseñanza del cálculo, lo cual obliga al profesorado a estudiar diferentes estrategias que fortalezcan el aprendizaje. Complemento de lo anterior, el presente estudio cuasiexperimental tuvo como propósito evidenciar que la aplicación de estrategias didácticas como el rompecabezas mejora significativamente la comprensión del cálculo en estudiantes de ingeniería industrial. Asimismo, este trabajo pretendió: diseñar una plantilla digital con estructura de rompecabezas basa-da en las cuatro etapas de la derivación y la integración; del mismo modo, aplicar test (fase 1), brindar la instrucción a los estudiantes sobre la dinámica del ejercicio (fase 2) y, por último, aplicar un pretest y un postest mediado por el rompecabezas, con el fin de analizar los datos con estadística descriptiva e inferencial (fase 3).
Antecedentes
A nivel mundial, en países como el Reino Unido, se presentan numerosos estudios en donde se muestra que juegos didácticos como el rompecabezas influyen, estimulan y motivan el aprendizaje (Hsu y Wang, 2018; Khamparia y Pandey, 2018). Sin embargo, además del juego, las TIC también cumplen la función de mejorar el aprendizaje y las habilidades matemáticas (García et al., 2018). En los Países Bajos, el juego se integra al proceso creativo en la didáctica del aprendizaje para contribuir a la apropiación de conceptos y para la competitividad (Akin y Akin, 1998; McEnroe y Farris, 2020; Stefan et al., 2019). Continuando en Europa, países como España apuntan al aprendizaje de las matemáticas con el uso de las TIC (Carvajal, 2019), no obstante, en Turquía el AA y AC son fundamentales en la enseñanza de este campo de estudio (Gay et al., 2020). En el continente americano, se observa un claro manejo de estrategias didácticas; es posible encontrar estudios de implementación del juego para interiorizar el conocimiento (Shawahna y Jaber, 2020), además de complementar el proceso creativo y el aprendizaje cooperativo en la enseñanza de las matemáticas (Seckel et al., 2019). Del mismo modo, la aplicación de las TIC orientadas al modelo didáctico de aprendizaje (Cabrera y Vitale, 2019) y las estrategias lúdicas como el ABJ representan una influencia positiva en el razonamiento y la interiorización de los conceptos matemáticos (Medina y Delgado, 2020).
Marco teórico o conceptual
Aprendizaje basado en juegos (AB J)
El ABJ es una estrategia educativa innovadora que motiva al estudiante a participar y trabajar en equipo (Hartt et al., 2020), cuyo diseño ha de tener en cuenta los resultados de aprendizaje para que este sea más eficaz (Nadolny et al., 2020). Así, el factor motivacional que constituye para los universitarios el tener un ambiente formativo agradable y divertido estimula el aprendizaje significativo (Whitton y Langan, 2019). También, con estudios como el realizado por López-Fernández et al. (2021) , en el que se compara la aplicación del aprendizaje tradicional en un grupo y del ABJ en otro, se mostró que ambos métodos permitieron una adecuada apropiación del conocimiento, aunque en el ABJ el factor determinante fue la motivación del estudiante (López-Fernández et al., 2021). Esta estrategia educativa también ayuda a comprender conceptos en el área matemática (Trouche et al., 2019; Wijaya et al., 2021); o al aplicarse torneos útiles para evaluar el conocimiento de los estudiantes y mejorar sus calificaciones en cursos matemáticos (Dziob et al., 2018). Sin duda, como se analiza en Shute et al. (2021) , las adaptaciones del juego educativo en el aula muestran mejoras significativas en las calificaciones, y en el análisis es importante incluir parámetros como el género y la etnia de los estudiantes. Así, el juego ha incursionado, no solo en la educación, sino también en la industria, en la que se han obtenido favorables resultados y experiencias representativas, como las temáticas de la industria 4.0 (Mortensen et al., 2018).
Aprendizaje basado en juegos digitales (AB JD)
La adaptación de nuevos juegos educativos digitales a las condiciones de aprendizaje de cada estudiante mejora los resultados formativos (Jafari y Abdollahzade, 2019; Kapon et al., 2019); sumado a esto, el aprendizaje lúdico también es significativo en el nivel universitario (Manzano-León et al., 2021). En la implementación de estas estrategias es importante tener en cuenta las actitudes y habilidades psicocognitivas de los participantes (Bontchev et al., 2018). Sin embargo, estudios experimentales analizan el ABJD no solo desde su efectividad, sino también respecto de las variables y los contextos que motivan a los participantes a entrenarse con metodologías basadas en juegos (All et al., 2021). Otro concepto para tener en cuenta en el ABJD, que ha tenido impactos positivos en el aprendizaje, es la competencia en el juego, ya que este factor apoya el aprendizaje en diferentes áreas, como las matemáticas y las ciencias (Chen et al., 2020). Además de incluir los logros y la motivación en este proceso, que permiten mejores resultados en las matemáticas, se debe respaldar con una adecuada base teórica (Es-Sajjade y Paas, 2020). La implementación del ABJD evidencia mejoras en las calificaciones posteriores de los estudiantes (Huang et al., 2020; Kiili et al., 2018), permite identificar necesidades educativas, mejorar la retención y persistencia del estudiante (Turner et al., 2018), mejorar el rendimiento y la actitud educativa, tanto en estudiantes con altos saberes previos como en los de bajos saberes previos (Hooshyar et al., 2021); además, ayuda a los docentes identificar errores en la comprensión de los temas y posiblemente a tener una mayor comprensión (López-Fernández et al., 2021).
Aprendizaje colaborativo (AC)
Sung y Hwang (2018) abordan la mejora y efectividad del proceso educativo con la implementación de juegos digitales apoyados en el AC, el compromiso y análisis del comportamiento en la resolución de problemas. No obstante, aunque estudios como el de Ruipérez-Valiente y Kim (2020) , mencionan que los juegos digitales aplicados en matemáticas reflejan resultados relevantes en el aprendizaje de niños y adolescentes, es de gran importancia seguir explorando cómo aplicar estas estrategias de forma efectiva, ya que en su trabajo, al integrar los juegos digitales en el aula se obtuvieron mejores resultados cuando los estudiantes aplicaron la estrategia de forma individual que cuando lo hicieron de forma colaborativa. Por el contrario, en el estudio de Ting et al. (2019) , se muestra cómo el AA por medio del AC basado en juegos mejora significativamente la comprensión conceptual en el cálculo diferencial. Asimismo, se evidencia que el aprendizaje en equipo mejora los resultados en la educación matemáticas (Ardiyani, 2018; Lewis et al., 2021). Los estudiantes universitarios en el área de matemáticas resaltan el uso del AC y la aplicación de tecnologías en la enseñanza (Hall et al., 2020), ya que son técnicas que fortalecen y han tenido impacto positivo en el aprendizaje universitario (Troussas et al., 2020).
Aprendizaje activo (AA)
La implementación del AA en el aula tiene un impacto positivo tanto en los resultados de aprendizaje y la participación de los estudian-tes como en las metodologías de los profesores que fortalecen el aprendizaje de los estudiantes (Talbert y Mor-Avi, 2019). Además, este enfoque se complementa muy bien con el uso de herramientas tecnológicas en el aula, al influir en una mayor participación de los estudian-tes (Caserta et al., 2021). Del mismo modo, el AA ha incursionado en la enseñanza de la robótica (Taylor et al., 2021), en la ingeniería aeroespacial como factor integrante de la motivación, que ayuda a mejorar el rendimiento académico (López-Fernández et al., 2019), al igual que en los programas de formación de profesores, donde se evidencian experiencias exitosas en la enseñanza (Lerum et al., 2021).
Aprendizaje mediado por las T IC
En la actualidad, el uso de las TIC en el aula no solo mejora la enseñanza, sino que se considera una innovación educativa (Backfisch et al., 2021); en el ámbito de la enseñanza de las matemáticas, facilita el aprendizaje (Delgado y Pérez, 2019; Medina et al., 2019). Por ello, se resalta el estudio de Chen y Wu (2020) , en el que la aplicación de las TIC con enfoque en enseñanza correctiva mejora las calificaciones en pruebas matemáticas. Igualmente, el uso de las TIC apoyadas en el juego tiene influencia positiva en la motivación y los resultados de la evaluación en las matemáticas (Pratiwi y Istiyowati, 2020), además, esta estrategia en combinación con el juego de roles (Doğantan, 2020), el AC y el aprendizaje invertido (Zheng et al., 2020), fortalecen la formación. Se destaca el estudio de Nousiainen et al. (2018) , que aborda las dificultades de los profesores al diseñar y aplicar una estrategia de aprendizaje mediada por las TIC en el aula teniendo como limitante, en muchas ocasiones, la poca competencia en el uso de herramientas digitales, lo cual implica un proceso educativo de prueba y error sin los mejores resultados. De ahí la importancia de fortalecer los conocimientos, las habilidades y las actitudes de los profesores en la aplicación de estas estrategias. Por consiguiente, es necesario el entrenamiento de los docentes en tecnologías educativas que permitan una innovación formativa (Silva et al., 2020).
Metodología
Es un estudio de tipo cuasiexperimental, con enfoque cualitativo-cuantitativo. Se utilizó una estrategia de ABJD con la implementación de un rompecabezas en el aula, para el proceso de derivación e integración indefinida. En el proceso de completar un rompecabezas se debe tener en cuenta el sentido de las fichas, ya que cada una aporta indicaciones para colocar la siguiente ficha y al final forman una estructura completa. Además, el rompecabezas permite el aprendizaje colaborativo ya que los estudiantes pueden interaccionar con sus compañeros (Schippers y Scheepers, 2020). Para el experimento se formaron tres grupos en cada asignatura con su respectivo estudiante líder, luego en reunión con el docente tutor se explicaron las reglas de juego del rompecabezas para su posterior ejecución (figura 1). Finalmente, para la medición de la estrategia se aplicó un pretest y postest sobre las propiedades básicas de la derivación e integración y se analizaron los resultados estadísticamente con una prueba no paramétrica.
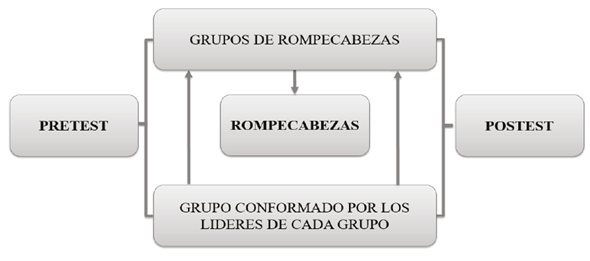
Fuente: elaboración propia. Nota: el grupo conformado por líderes recibe la instrucción del tutor, luego en su grupo de rompecabezas resuelven el ejercicio.
Figura 1 Flujograma actividad del rompecabezas
Lugar de estudio
Este estudio fue realizado en la sede norte de la Fundación Universitaria de Popayán (FUP), en el programa de Ingeniería Industrial. Esta sede, llamada también sede Alvaro Ulcué Chocué, está ubicada en el norte del departamento del Cauca en el municipio de Santander de Quilichao (FUP, 2018), cuyas coordenadas geográficas son 3° 00’ 19’’ N 76° 29’ 14’’ W según la aplicación Google Earth (figura 2).
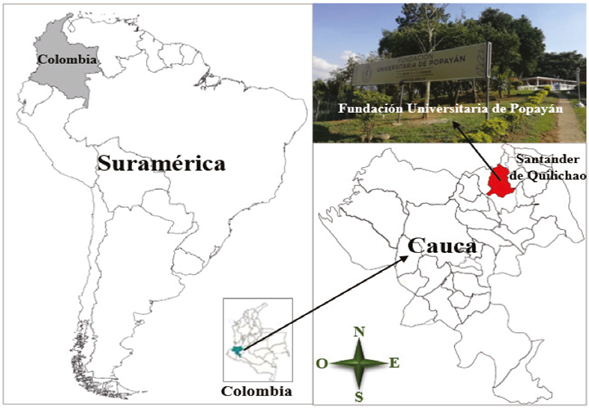
Fuente: adaptado de Secretaría de Educación y Cultura (s. f.); Montoya (2014) ; y SaludCauca (2020).
Figura 2 Mapas de Sudamérica, Colombia, el departamento del Cauca y el municipio de Santander de Quilichao con la ubicación de la Fundación Universitaria de Popayán sede norte
Participantes
Se utilizó un muestreo intencional no probabilístico, ya que es apropiado y confiable en este tipo de estudios cuasiexperimentales (Campbell et al., 2020). El total de participan-tes fue de 178 (N = 178), correspondientes a 70 estudiantes de la asignatura Cálculo Diferencial y 108 de Cálculo Integral. Estos estudiantes son los inscritos a las dos asignaturas durante los años 2016 al 2020, a los cuales se les aplicó la estrategia de ABJD por medio del rompecabezas.
Diseño metodológico y medición
Fase 1
Se diseñó un rompecabezas por medio de una plantilla digital con la aplicación Power Point (Microsoft Office). El instrumento consta de cuatro columnas que definen las estrategias para resolver las derivadas e integrales indefinidas, diez filas que definen la cantidad de ejercicios para resolver, por lo tanto, el rompecabezas está formado por cuarenta piezas, donde se muestran diez ejercicios con su respectiva solución (figura 3).

Se muestran dos plantillas de cuarenta fichas cada una con sus respectivos espacios para ubicarlas en sentido lógico conforme al proceso de derivación e integración indefinida. Fuente: elaborado con base en los datos de Larson y Edwards (2016)
Figura 3 Plantillas del rompecabezas para la derivación e integración indefinida
En cuanto al pretest y postest, se diseñó un cuestionario con cuatro aspectos sociodemográficos y cinco ejercicios referentes a cada tema; se utilizó la misma prueba para el pretest y el postest (figura 4). La ejecución de estas pruebas, de manera análoga, tuvo cuatro momentos: clase magistral para conceptualizar los temas, pretest, estrategia del rompecabezas y, por último, el postest.

Se muestran el pretest y postest: (A) Cálculo Diferencial, (B) Cálculo Integral. Fuente: elaboración propia, con base en los datos de Larson y Edwards (2016) .
Figura 4 Pretest y postest para la asignatura Cálculo Diferencial e Integral
Fase 2
Para la instrucción sobre la dinámica del juego y su ejecución, se establecieron en las asignaturas tres grupos para la aplicación de la estrategia, los cuales tendrán la plantilla digital (rompecabezas) en una computadora portátil. Los estudiantes podrán disponer de una hoja en blanco y un lápiz para realizar operaciones. Cada grupo de rompecabezas debe analizar la tabla con su líder, quien, previo debate sobre el contenido del tema en reunión de líderes, será el tutor del grupo e impulsor para que salgan adelante como equipo. El grupo ganador será el que complete el rompecabezas, de manera adecuada, en el menor tiempo (duración máxima 30 minutos); además, tendrá un incentivo académico de 0,5 décimas en la nota definida de la asignatura.
Al final, se realizará la retroalimentación de la actividad e intervenciones de los grupos. Igualmente, los estudiantes tendrán la oportunidad de enviar las reflexiones de la actividad vía correo electrónico al docente.
Fase 3
Los datos sociodemográficos se compararon de forma descriptiva con frecuencias porcentuales y luego se contrastaron con el pretest y el postest. La identificación de diferencias significativas entre el pretest y postest e impacto de la actividad el rompecabezas se realizó por medio de una prueba no paramétrica de Wilcoxon para muestras relacionadas, una vez verificada la normalidad de los datos. En los procesos anteriores se utilizó el software IBM SPSS Statistics, versión 25.
Resultados y análisis
La aplicación del pretest y postest se usó para recolectar información sociodemográfica de los estudiantes de las asignaturas Cálculo Diferencial e Integral, donde la mayoría (74,7 %) es procedente de Santander de Quilichao, el 85,5 % están ubicados en zona urbana y el 62,9 % es de estrato medio-bajo (gráfica 1). Posteriormente, estos datos sirvieron para realizar un análisis comparativo entre los grupos y sus calificaciones antes y después de la aplicación del rompecabezas.
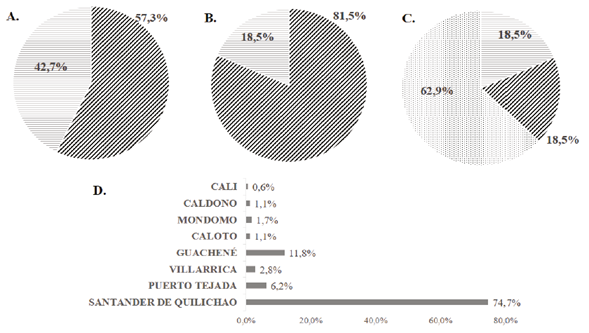
Análisis descriptivo de los aspectos sociodemográficos: (A) género: femenino (trama gris), masculino (trama negra); (B) zona: rural (trama gris), urbana (trama negra); (C) estrato: bajo-bajo (trama gris), bajo (trama negra), medio-bajo (trama gris punteada); y (D) procedencia.
Gráfica 1 Aspectos sociodemográficos de los estudiantes
La prueba de Wilcoxon para muestras relacionadas se analizó en comparación con aspectos sociodemográficos de los estudiantes, como el género, la procedencia, la zona y el estrato (Tabla 1). En este sentido, la revisión de la eficacia del rompecabezas en contraste con estos aspectos tuvo mejoras significativas (p < 0,05) entre las calificaciones del pretest y postest en el grupo de estudiantes procedente de Santander de Quilichao con las siguientes características: (a) ambos géneros, zona urbana, estrato medio-bajo y pertenecientes a las dos asignaturas; (b) ambos géneros, zona rural, estrato bajo-bajo y de la asignatura Cálculo Diferencial; (c) género masculino, zona rural, estrato bajo-bajo y de la asignatura Cálculo Integral. Con la misma mejora significativa, los grupos de estudiantes procedentes de los municipios de Puerto Tejada y Guachené de género femenino, zona urbana, estrato bajo y de la asignatura Cálculo Integral. Las otras interacciones de variables sociodemográficas con los resultados del pretest y postest no demuestran diferencias significativas (p > 0,05).
Tabla 1 Prueba no paramétrica de Wilcoxon para el pretest y postest con variables sociodemográficas
| Zona | Estrato | Género | Asignatura | Procedencia | Estadísticos de prueba a | Postest - Pretest |
|---|---|---|---|---|---|---|
| Urbano | Bajo | Masculino | Cálculo Diferencial | Villarrica | Z | -1,342 b |
| Sig. asintótica (bilateral) | 0,180 | |||||
| Guachené | Z | -1,826 b | ||||
| Sig. asintótica (bilateral) | 0,068 | |||||
| Cálculo Integral | Puerto Tejada | Z | -1,604 b | |||
| Sig. asintótica(bilateral) | 0,109 | |||||
| Guachené | Z | -1,633 b | ||||
| Sig. asintótica(bilateral) | 0,102 | |||||
| Femenino | Cálculo Diferencial | Guachené | Z | -1,342 b | ||
| Sig. asintótica (bilateral) | 0,180 | |||||
| Cálculo Integral | Puerto Tejada | Z | -2,207 b | |||
| Sig. asintótica (bilateral) | 0,027 | |||||
| Guachené | Z | -2,379 b | ||||
| Sig. asintótica (bilateral) | 0,017 | |||||
| Mediobajo | Masculino | Cálculo Diferencial | Santander de Quilichao | Z | -3,942 b | |
| Sig. asintótica (bilateral) | 0,000 | |||||
| Cálculo Integral | Santander de Quilichao | Z | -5,848 b | |||
| Sig. asintótica (bilateral) | 0,000 | |||||
| Femenino | Cálculo Diferencial | Santander de Quilichao | Z | -3,736 b | ||
| Sig. asintótica (bilateral) | 0,000 | |||||
| Cálculo Integral | Santander de Quilichao | Z | -4,202 b | |||
| Sig. asintótica (bilateral) | 0,000 | |||||
| Rural | Bajo-bajo | Masculino | Cálculo Diferencial | Santander de Quilichao | Z | -2,214 b |
| Sig. asintótica (bilateral) | 0,027 | |||||
| Mondomo | Z | -1,34 2b | ||||
| Sig. asintótica (bilateral) | 0,180 | |||||
| Cálculo Integral | Santander de Quilichao | Z | -2,375 b | |||
| Sig. asintótica (bilateral) | 0,018 | |||||
| Guachené | Z | -1,342 b | ||||
| Sig. asintótica (bilateral) | 0,180 | |||||
| Femenino | Cálculo Diferencial | Santander de Quilichao | Z | -2,371 b | ||
| Sig. asintótica (bilateral) | 0,018 | |||||
| Cálculo Integral | Santander de Quilichao | Z | -1,342 b | |||
| Sig. asintótica (bilateral) | 0,180 | |||||
| Guachené | Z | -1,342 b | ||||
| Sig. asintótica (bilateral) | 0,180 |
Nota: Evidencia la prueba no paramétrica de muestras relacionadas aplicada al pretest y postest comparando variables sociodemográficas. a. Prueba de rangos con signo de Wilcoxon. b. Se basa en rangos negativos.
Fuente: elaboración propia.
Los resultados de la técnica de aula Rompecabezas, sin tener en cuenta agrupaciones con aspectos sociodemográficos, pero sí la totalidad de la muestra, dejan ver diferencias significativas (p < 0,05) entre puntuaciones del pretest y postest en la prueba estadística no paramétrica utilizada, lo cual evidencia mejoras a nivel global en el aprendizaje de los estudiantes (Tabla 2).
Tabla 2 Prueba no paramétrica de Wilcoxon para el pretest y postest
| Rangos | Prueba de rangos con signo de Wilcoxon | |||||
|---|---|---|---|---|---|---|
| N | Rango promedio | Suma de rangos | Postest-pretest | |||
| Rangos negativos | 0 a | 0,00 | 0,00 | |||
| Postestpretest | Rangos positivos | 172 b | 86,50 | 14878,00 | Z | 11,392 d |
| Empates | 6 c | Sig. Asintótica (bilateral) | 0,000 | |||
| Total | 178 | d. Se basa en rangos negativos. | ||||
| a. Postest < Pretest | ||||||
| b. Postest > Pretest | Media pretest: 2,409 | |||||
| c. Postest = Pretest | Media postest: 4,284 |
Nota: prueba estadística no paramétrica considerando el total de la muestra seleccionada.
Fuente: elaboración propia.
Es un estudio innovador ya que aplica el ABJD, con el apoyo de un rompecabezas, mejorando la comprensión del cálculo, siendo esta Área, fundamental en la formación de los ingenieros. Asimismo, integrar el aprendizaje colaborativo a esta estrategia didáctica, con la finalidad de promover el trabajo en equipo. Por otro lado, el establecimiento de incentivos en el aula, es un factor determinante en la motivación a la apropiación del conocimiento, como lo menciona Rahimi et al. (2021) . Este concepto sirvió como apoyo al éxito del presente experimento aplicado a estudiantes de ingeniaría industrial, que sirvió para aumentar los resultados en el aprendizaje del cálculo, como se ha demostrado también en Medina et al. (2019) y Chen y Wu (2020) .
Este estudio tuvo resultados equivalentes a los alcanzados por Bontchev et al. (2018) , Dziob et al. (2018) , Hsu y Wang (2018) , Kiili et al. (2018) , Chen y Wu (2020) , Delgado y Pérez (2019) , Medina et al. (2019) , Pratiwi y Istiyowati (2020) , Shawahna y Jaber (2020) , All et al. (2021) y Hooshyar et al. (2021) , referente a que los estudiantes mejoraron las calificaciones en la prueba posterior, al realizar una actividad de ABJD, además sirve para definir la pertinencia y confiablidad de esta. Del mismo modo, la estrategia didáctica aplicada tiene similitud con los ejercicios realizados por Hsu y Wang (2018) y Bontchev et al. (2018), donde el instrumento aplicado en el aula fue un rompecabezas.
Los procedimientos del cálculo son relativamente complejos, aquí es donde entran en juego los saberes previos y las fortalezas numéricas que tengan los estudiantes desde su formación en la secundaria. No obstante, este estudio tuvo un momento de reflexión de los estudiantes frente a la estrategia didáctica y el uso de la tecnología en el aula, considerando que son técnicas que deberían aplicarse con mayor frecuencia en la enseñanza de las matemáticas por parte de los docentes, tal cual se resalta en el estudio de Carvajal (2019) .
El enfoque de este experimento pedagógico sirvió para contrastar aspectos sociodemográficos de los estudiantes entre los resultados de la estrategia aplicada. El uso de esta información demográfica fue consistente con los trabajos de Bontchev et al. (2018) , Ting et al. (2019) , Shawahna y Jaber (2020) , Rahimi et al. (2021) y Backfisch et al. (2021) , aunque en ellos fue tratada como información secundaria con estadística descriptiva, contrario al presente estudio, en donde en el análisis se tuvo en cuenta estadísticamente la eficacia de la estrategia del rompecabezas en los grupos de participantes.
Conclusiones
Este estudio en la fase 1 de diseño logró superar las limitaciones del profesorado en lo referente a la construcción de instrumentos digitales y lo acercó más al fortalecimiento de sus áreas de competencias pedagógicas y creativas. En lo que respecta a la fase 2, de socialización de la estrategia, sumada a una clara y adecua instrucción, esta tuvo un valor significativo en el factor motivacional de los estudiantes, que tuvo un resultado favorable en la actividad del rompecabezas. Finalmente, en la fase 3, el análisis de los datos demostró una buena fiabilidad en el pretest y postest, además de la efectividad de los rompecabezas en el aprendizaje.
Conviene señalar que los resultados del estudio reflejan que el diseño y uso de estrategias didácticas en el aula, como el ABJD, integrada al AA y el AC, fortalece la estructura metodológica del docente y enriquece la aplicación de instrumentos que apuntan al descubrimiento del conocimiento y la búsqueda constante de herramientas de aprendizaje con enfoque motivacional. Este trabajo revela cómo el desarrollo de estos sistemas de aprendizaje mejora las habilidades matemáticas en estudiantes de ingeniería; además, como la vinculación de aspectos sociodemográficos en estos análisis refleja las oportunidades de mejora por llevar a cabo en el ingreso potencial de un estudiante de ingeniería y poder fortalecer sus saberes previos.
Aunque los resultados demuestran que el rompecabezas mejora significativamente el aprendizaje de los estudiantes en las áreas de Cálculo Diferencial e Integral, se evidencia un mejor impacto en los estudiantes de estrato medio-bajo pertenecientes a la zona urbana, en los que, en todos los casos, la estrategia educativa trajo una mejora significativa en el aprendizaje del cálculo, con respecto al pretest y postest. Esta situación nos lleva a reflexionar cómo vienen preparados los estudiantes desde la secundaria y la fortaleza de los saberes previos en matemáticas, cuando estos pertenecen a estratos más bajos o son de la zona rural; aunque es una apreciación que no se puede generalizar, el presente estudio sugiere que este aspecto sí influyó en el resultado. En este sentido, es importante que los docentes mejoren sus competencias educativas y puedan implementar en el aula actividades de este tipo que evidentemente aumentan el rendimiento académico, la motivación y la apropiación del conocimiento. Para finalizar, este estudio podría servir en futuras investigaciones en donde se aplique la técnica de aula del rompecabezas en diferentes áreas del conocimiento, pero especialmente en las consideradas ciencias duras.















