English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introduction
Graphene is a two-dimensional material made up by strongly cohesive carbon atoms through covalent bonds that present a sp 2 hybridization, these atoms are arranged in a honeycomb packed structure (hexagonal lattice) of one-atom thick. As well, this two-dimensional system is currently being investigated with great intensity due to its incredible mechanical, electronic, optical, magnetic, and thermal properties [1-3]. For this reason, researchers have been finding a wide variety of applications such as in nanoelectronics [4, 5], energy storage [6, 7], water purification [8] and as coated composite materials [9]. In addition to these applications, the nanoporous graphene (NPG) membranes promise great utility in seawater desalination [10, 11], carbon dioxide separation [12-14] and the nanoribbons of NPG may be thought of as unidimensional channels for electronic applications (nanocircuity), i.e., for directing electrons through predesigned paths via nanoporous [15]. In this scenario, previous studies have reported that permeability of the NPG membrane is approximately three orders of magnitude greater than the latest generation (commercial) reverse osmosis, where salt ions are rejected at 100 % [10].
On the other hand, the mechanical properties of pristine graphene have been extensively investigated by theoretical methods and experimental techniques. For example, Lee et al [16] reported Young's modulus of ~ 1.0 TPa and maximum stress of ~ 130 GPa, this study was performed on a series of graphene monolayers with a coated tip diamond using atomic force microscopy (AFM). Furthermore, Gomez-Navarro et al. [17] found Young's modulus of 0.25 ± 0.15 TPa for a reduced graphene oxide monolayer using AFM nanoindentation. However, Paci et al. [18] investigated using Monte Carlo (MC) method and molecular dynamics (MD) simulations, that oxidation process significantly decreases Young's modulus and the fracture stress of graphite oxide.
In this research field, other recent works mention the manufacture of NPGs using experimental techniques [19, 20]. For example, Bai et al. [21] reported for the first time the synthesis of NPG membranes with variable periodicity using polymer block lithography. In addition, Kostoglou et al. [19] synthesized an NPG-based material with a large surface area by wet chemical reduction of graphene oxide in combination with lyophilization (freeze-drying). The NPG membrane can be used for hydrogen adsorption and gas separation [19]. Also, there are some reports on the study of the mechanical properties of NPG using theoretical methods. For example, Carpenter et al. [22] studied the elastic responses of graphene nano-meshes through molecular static and MD simulations, performing uniaxial tensile deformation tests. Also, they calculated that the modulus of elasticity is independent of the arrangement of the pore structure. In the same way, the elastic modules show more sensitivity to porosity with increasing temperature. Likewise, Liu and Chen [23] carried out MD simulations with the objective to investigate the mechanical properties of the NPG membranes under uniaxial tensile tests where they determined an important relationship between the stress-strain curve and the porosity.
In order to contribute the knowledge about the NPG membranes, this paper presents a systematic study of the mechanical properties of different geometric shapes of pores under uniaxial tensile at room temperature. Afterward, to find the geometric shape of the NPG with the highest tensile strength, the mechanical properties of the NPG were also studied by varying the pore size. The next section describes the models of the NPG membranes for four geometric shapes and the details of the computational method. In the third section, the results obtained with its respective discussions are presented and finally, in the fourth section, conclusions of the present work are presented.
1. NPG membrane models and simulation method
1.1. Models of NPG membranes
The structures of the graphene nanosheets were generated using the software quantumATK [24], where the area of each nanosheet was 50x50 Å2, and the volume of the system was determined from the area of the nanosheet with a thickness of 3.4 A [25]. In addition, the bond length parameter of the graphene nanosheet was considered as α c-c = 1.42 Å. To generate the NPG, differents vacancies at the center of the pristine graphene nanosheet were used. For example, to obtain a nanopore with a hexagonal, rhombic, rectangular, or triangular shape, a polygon with a certain number of sides depending on the shape was used to subtract the atoms at the center of the nanosheet and thus obtain the NPG membranes (as shown in figure 1). Additionally, it is worth mentioning that due to the discrete nature of the distribution of carbon atoms in the graphene, the shape of the nanopore may not be perfectly geometric, which is consistent with previous studies on the permeability of the NPG membrane [10].
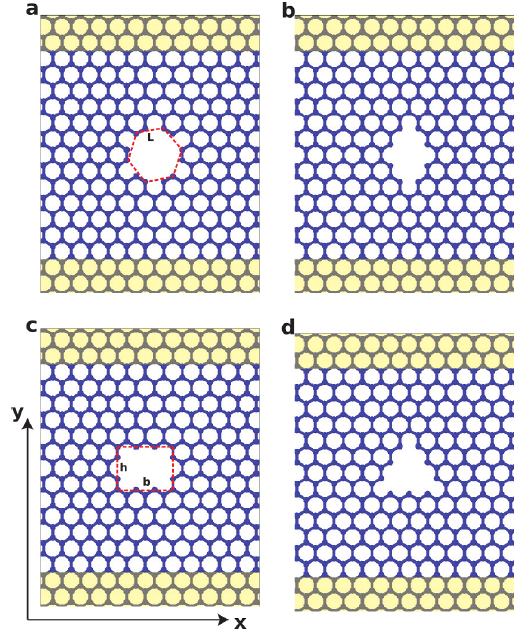
FIGURE 1 Atomic configuration of nanoporous graphene membranes with pores: (a) hexagonal (NPG-hex), (b) rhombic (NPG-rho), (c) rectangular (NPG-rec) and (d) triangular (NPG-tri). The yellow regions are fixed to uniaxially strain the NPG membranes in the armchair direction (parallel to the "y" axis). Similarly in the zigzag direction.
1.2. Simulation Details
To obtain the mechanical properties, such as stress-strain curves and Young's modulus of the NPG membranes, the LAMMPS package was used based on the MD method [26], with an AIREBO atomic interaction potential for carbon atoms. In addition, a cut-off distance of this potential was equal to 2.0 Å, because previous studies mention that cut-off distance for AIREBO potential should be taken in the range from 1.92 to 2.0 Å, to avoid non-physical post-hardening behavior [27, 28] and obtain results consistent with the Density Functional Theory (DFT) calculations [29].
On the other hand, in all simulations the fixed regions were selected at the ends of the NPG membrane, to apply an uniaxial tensile (see yellow regions shown in figure 1). Periodic boundary conditions were used on the "x-y" plane. Also, before applying the tension, the NPG membranes were relaxed at 300 K with a canonical ensemble (NVT) controlled by Nose-Hoover thermostat to reach the state of thermodynamic equilibrium. Subsequently, the system was subjected to tension displacing the fixed regions of the NPG membrane from each other. The simulation was performed with a strain rate of 0.01ps-1 and a time step of 0.5 fs for the integration of the equations of motion.
First, to study the behavior of the stress-strain curve under uniaxial tensile, the average of the nominal stress and the viral stress was used. Then the total stress was determined by averaging all the stress of the carbon atoms of the membrane excluding those atoms that are in the fixed regions. All these steps were considered in order to study the effects of shape and size of the pores of the NPG membranes on the mechanical properties. All atomic visualizations of the NPGs configurations were using the software OVITO [30]
1.3. AIREBO Potential
For atomic carbon-carbon (C-C) interactions, AIREBO potential was used (Adaptative Intermolecular REBO potential), AIREBO potential is made up of three terms,
where, E REBO ij , E LJ ij and E TORSION ijkl represent the following: the REBO potential of hydrocarbons, long-range interactions (Lennard-Jones potential) and the molecular torsions of the system, respectively.
For REBO term of the interatomic potential, a cut-off function is defined to limit the interaction between the nearest neighbors,
where Dmax - Dmin defines a range in which the function fc takes values between 1 and 0. Also these default values of the C-C interaction are 2.0 Å and 1.7 Å, respectively.
2. Results and Discussion
2.1. Shape effect on NPGs at 300 K
In this first part of the results, the effect of nanopores on pristine graphene nanosheets (pristine-G) is discussed. The nanopores with geometric shapes to be considered are: hexagonal (NPG-hex), rhombic (NPG-rho), rectangular (NPG-rec), and triangular (NPG-tri). The representations of these NPG membranes are shown in figures 1 (a)-(d). These NPG membranes have a porosity of 0.97% (NPG-hex), 0.64% (NPG-rho), 0.81 % (NPG-rec) and 0.73% (NPG-tri) in the armchair direction and 0.98% (NPG-hex), 0.69 % (NPG-rho), 0.86 % (NPG-rec) and 0.78 % (NPG-tri) in the zigzag direction, respectively. Porosity is defined as the ratio between the atoms that are removed by generating the nanopore and the total number of atoms in the pristine graphene nanosheet [31].
The shape effect is observed in the stress-strain curves shown in figure 2. Uniaxial tensile was subjected in both armchair and zigzag directions to probe the anisotropy of the mechanical properties (chirality of the graphene nanosheet). The uniaxial stress-strain responses of the NPG membranes show linear behaviors for small strain rates (<0.03) independent of chiral directions (see figures 2 (a) and (b)). These behaviors correspond to the elastic region due to the fact NPG membranes (porosity ~1 %) have a very low porous structure compared to the pristine graphene nanosheet.
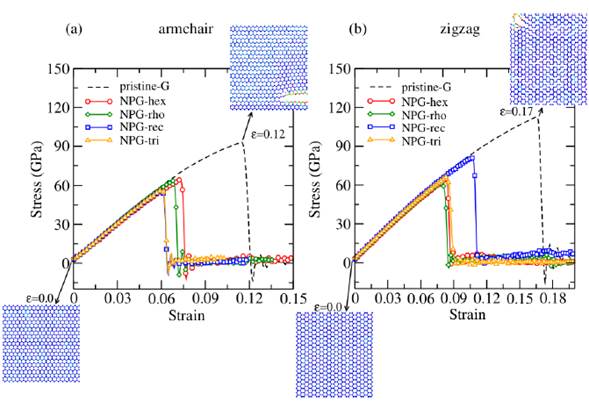
FIGURE 2 Stress-strain curves of NPG and nanosheet (pristine-G) membranes under uniaxial tensile in the direction of (a) armchair and (b) zigzag for four types of pores shown in figure 1. Selective snapshots of the structural evolution are shown for initial and fracture deformations of the pristine-G.
Furthermore, the results indicate that the linear and nonlinear regions of the stress-strain curves are different for a greater increase in uniaxial strain along with the armchair and zigzag directions, respectively. This mechanical behavior confirms the expected anisotropic responses of the NPG membranes, similar to the pristine-G. In the case of the pristine-G, the fracture stresses along with the armchair and zigzag direction were 93 GPa and 113 GPa with maximum fracture strains, εmax, of 0.12 and 0.17, respectively (see the dashed lines in figures 2 (a) and (b)). Fracture stress is defined as the maximum tensile stress that membranes can withstand before rupture. The stiffness of the pristine-G in the zigzag direction under uniaxial traction has already been reported before [32, 33].
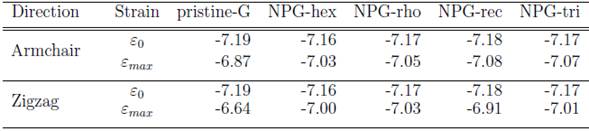
The NPG membranes with different pore shapes show a decrease in fracture stress compared to pristine-G. This decrease in the NPG membranes suggests that stretching capacity is reduced because the C-C bonds are limited as a consequence of the vacancies generated in the center of the graphene nanosheet. This characteristic is independent of the chiral direction maintaining an anisotropic response. In figure 2 (a) it is observed in the armchair direction the NPG-hex presents a greater fracture stress and fracture strain (65 GPa y 0.07) compared to other pores. Similarly, in figure 2 (b) NPG-rec presents a greater fracture stress and fracture strain (81 GPa and 0.11) in the zigzag direction, showing to be less fragile than the NPG-hex. Consequently, the highest accumulated energy of NPG-hex / NPG-rec after pristine-G is -7.03 (eV/atom) / -6.91 (eV/atom) at the point of e max for the armchair / zigzag directions, respectively (see table 1). It is worth noting that pristine-G is more stable before deformation because it has lower energy than the rest of the NPGs in both tensile directions.
TABLE 1 Energy per atom, E (eV/atom), during the uniaxial tensile process for initial strain, ε 0 , and fracture strain, ε max , for the NPG and pristine-G
It is worth mentioning that nanopores were simulated in different regions of the center, for example, positioned at the edges of the graphene membrane. The results for the armchair direction with hexagonal nanopore and porosity of 0.97 % show that the fracture stress (64 GPa) presents a slight decrease compared to the hexagonal nanopore located in the center of the membrane (65 GPa). The same happened for a fracture stress in the zigzag direction. However, the fracture strain does not show considerable changes for both directions ε max ≅ 0.07
Figures 3 (a) and (b) show the radial distribution functions at 300 K of the NPG membranes that present greater rigidity. The g(r)s show a structural order for an initial strain of 0.0.
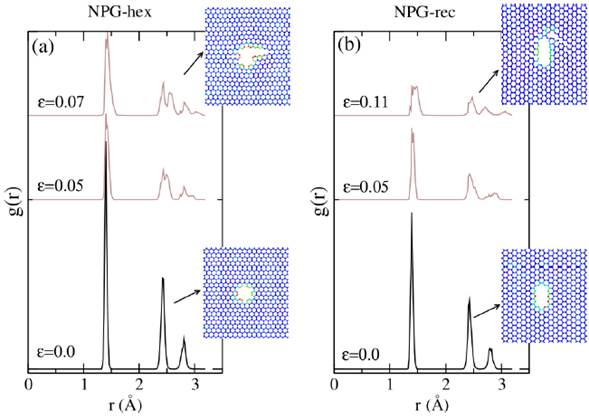
FIGURE 3 Radial distribution functions of (a) NPG-hex and (b) NPG-rec membranes for various strain rates, showing the structural evolutions for an initial and fracture strain.
However, this observed structural order at the peaks of varies during tensile, i.e., the distance between the first, second, and third neighbors changes due to the stretching of the C-C bonds until reaching a fracture stress (for NPG-hex and NPG-rec are 0.07 and 0.11, respectively). It is appropriate to comment that in both systems it is observed that fracture is generated around the pores (see structural evolutions in figure 3). Similar results on the mechanical properties of NPGs membranes were recently obtained and reported [31, 34, 35].
2.2. Size effect on NPGs at 300 K
The effect of pore size on NPG-hex and NPG-rec membranes is analyzed and discussed below due to they have a higher tensile strength. This observation on higher stress and fracture strain provides an applicability as a filter for seawater desalination [8, 10].
On the other hand, to generate the pores located in the center of the membrane with different sizes, the surface area of the pore is increased in relation to the hexagonal area (
) and rectangular area (b.h) respectively (as shown in the figures 1 (a) and (c)). The configuration of different pore sizes is shown in figures 4 (a) and (b). The pore areas are: NPG-hex1=20.98 Å2, NPG-hex2=36.72 Å2, NPG-hex3=68.19 Å2, NPG-hex4=131.12 Å2, NPG-hex5=194.07 Å2, NPG-rec1=31.47 Å2, NPG-rec2=41.96 Å2, NPG-rec3=62.94 Å2, NPG-rec4=83.92 Å2 and NPG-rec5=104.90 Å 2. In addition, the membranes have a porosity of 0.48% (NPG-hex1), 0.97% (NPG-hex2), 1.94% (NPG-hex3), 3.4% (NPG-hex4) and 4.38% (NPG-hex5) in the armchair direction and 0.86 % (NPG-rec1), 1.21 % (NPG-rec2), 1.9% (NPG-rec3), 2.6% (NPG-rec4) and 3.3% (NPG-rec5) in the zigzag direction, respectively.
Figures 4 (c) and (d) show linear-elastic responses for small strain (<0.03) independent of pore size and chiral direction (anisotropy). As the strain rate increases, the anisotropic mechanical response of the NPG membranes is observed notoriously. Furthermore, fracture stress and fracture strain vary as a function of size and / or porosity for both hexagonal and rectangular pores. However, in figure 4 (d) it is noted that systems subjected to uniaxial traction in the zigzag direction always show greater rigidity independent of the pore size and even of the pore shape (see figure 2 (b)).
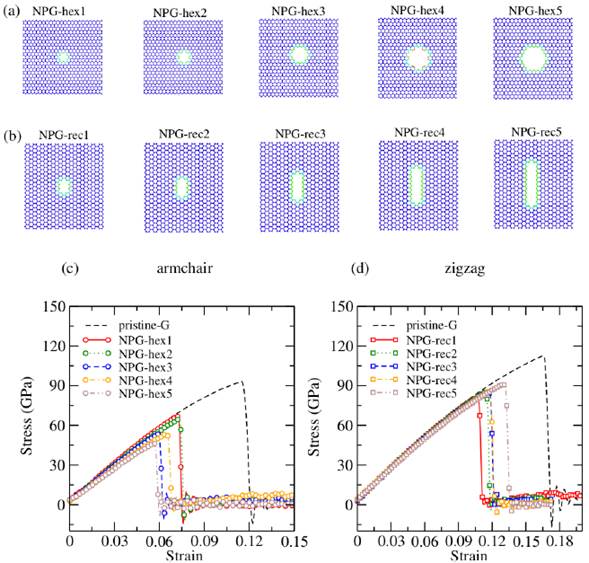
FIGURE 4 Membranes of (a) NPG-hex and (b) NPG-rec for different sizes, whose porosities vary in a range from 0.48% to 4-38% (NPG-hex1 to NPG-hex5) and from 0.86% to 3.3% (NPG-recl to NPG-rec5). Stress-strain curves for the membranes of (c) NPG-hex in the armchair direction and (d) NPG-rec in the zigzag direction, both for five different pore sizes shown in (a) and (b), respectively.
To further analyze the underlying uniaxial tensile mechanism, the elastic modulus and the change of the C-C bond lengths during strain are determined. For Young's modulus of elasticity, the values of the uniaxial stress-strain curve are adjusted for the strain rates below e <0.01. It is worth mentioning, that the slope of the curve in the linear part gives us the Young's modulus of the NPG membranes. In figure 5 (a) it is observed, that the modulus decreases as the pore size increases, similar to previous studies [31]. Furthermore, this indicates that higher values of the modulus show an immediate response to deformation (NPG-hex). In contrast, lower modulus values are obtained when the porosity is higher for NPG-hex5 and NPG-rec5 membranes (4.38 % and 3.3 %), respectively.
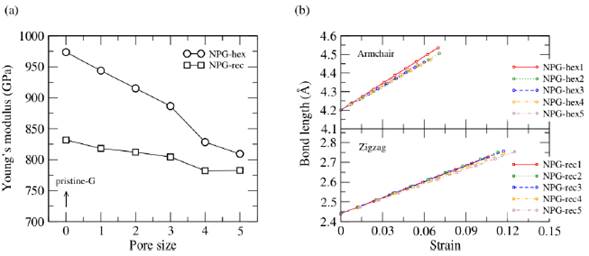
FIGURE 5 (a) Variation of Young's modulus of NPG membranes as a function of pore size. (b) Variation of the bond lengths of the NPG membranes with respect to the uniaxial tensile strain for armchair and zigzag direction.
Additionally, the variation in bond length in a certain tensile direction shows how quickly the C-C bonds change during strain. Figures 5 (b) show these changes in the C-C distances of the NPG-hex and NPG-rec membranes. The bond lengths increase linearly (L ≈ L 0 + Δ x ε) as the strain increases up to the respective fracture strain for each system. The difference between the chiral directions is the speed (Δ) at which the C-C distance increases. For armchair direction we have L ≈ 4.2 + 4.4x ε and zigzag L ≈ 2.44 + 2.7x ε (averaging the slopes of the five lines). These observations may explain why the zigzag direction has large values of fracture stress and fracture strain compared to the armchair direction. [32].
Conclusions
Our MD simulations reveal the behavior of the mechanical responses of the NPG membranes under uniaxial tensile using AIREBO interatomic potential. Stress-strain curves, structural evolution, and Young's modulus concerning to shape and size and/or porosity of the nanopore were examined. For the shape effect, the results show a decrease in fracture stress and fracture strain compared to pristine-G. The NPG membranes with tensile strength have a hexagonal and rectangular shape. In general, the mechanical responses in the armchair and zigzag directions are different, this indicates that the NPG membranes have a chiral anisotropy similar to pristine-G. The results regarding the effect of pore size show a decrease in Young's modulus with respect to pore size. Furthermore, the lowest Young's modulus value is obtained when the porosity is greater in the NPG-hex and NPG-rec membranes. Finally, it was observed that the C-C bond length in the zigzag direction varies slower than in the armchair direction as the strain increases.
