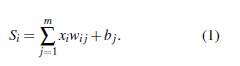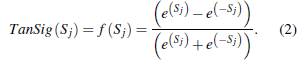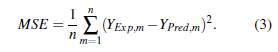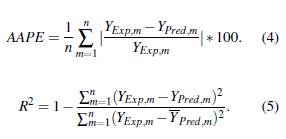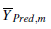1 Introduction
Currently, cutting-edge technology is used in industrial processes to tackle different types of problems that arise when working with multiphase flows, covering the food industry, Oil & Gas, thermoelectric plants, among others [1], [2]. There is a need to increase the accuracy in the description and analysis of the multiphase flow phenomena that are presented in these processes [3]. Therefore, these processes need to be investigated in depth to determine the phenomenological or hydrodynamic behavior of the working fluids [4, 5].
Artificial intelligence (AI) is used to perform multiphase flow analysis to be able to identify the global and local flow regime [6], using the probability distribution to train an intelligent system based on Artificial Neural Networks (ANN) [7]. To identify low patterns, analyzes have been carried out applying intelligent algorithms based on Support Vector Machine (SVM) [8]. Neural networks were used by [9] to identify the low regime having as inputs the Probability Density Functions (PDF) and the signal in time that gives the electrical impedance of the fluid.
In order to characterize low patterns from the application of fuzzy logic, [10] studied topographic images obtained with an intelligent system. A fluid pressure signal as a function of time was used by [11] to train an intelligent system based on the Elastic Maps Algorithm (EMA) technique identifying the flow pattern. A combination of artificial intelligence and Principal Component Analysis (PCA) methods to determine low based on an electrical signal of pressure as a function of time was developed by [12].
To obtain the holdup and low rate, [13] compared three AI algorithms based on artificial neural networks (ANN), genetic propagation (GP), and Support Vector Machine (SVM). Studies for two phases of water-air low in a horizontal pipeline using artificial intelligence were carried out by [14], training a neural network with the spectrum of bands acquired by hydrophones. Applied artificial intelligence techniques based on neural networks were developed by [15], where the pressure signal as a function of time was the input of the network to determine the flow pattern. In the study carried out by [16], a back-propagation neural network was trained to determine the flow regime in a horizontal pipe.
Studies for training a neural network from low characteristics and a sensor based on electrical capacitance as inputs, to obtain the holdup of water of two-phase oil-water low were developed by [17, 18]. In a horizontal pipe, [19] analyzed flow patterns and data generated from photographs and signals generated by an optical probe using neural networks.
This study aims to study the viability of the use of neural networks in the generation of a predictive model that allows obtaining the holdup of a two-phase low in a horizontal pipe. First, several multilayer neural networks are trained with back-propagation by modifying the number of neurons that make up the hidden layers. Then, the best model is selected from the comparison of the errors presented when generating the predictive model.
2 Experimental Methodology
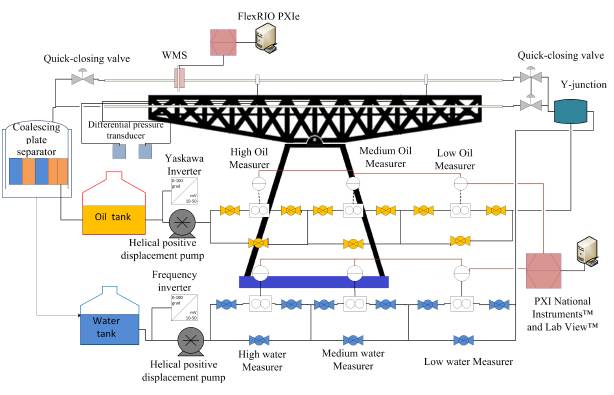
The experimental tests were done in the Industrial Multiphase Flow Laboratory (LEMI), São Carlos School of Engineering (EESC /USP), Brazil. The experimental set up is shown in Figure 1.
For this study, a horizontal pipeline of 12 [m] with 80 [mm] internal diameter and 4.5 [mm] thick was used. The fluid was water with a viscosity of 1 [cP] and a specific density of 997 [kg/m3] at room temperature, together with mineral oil M600 with a viscosity of 180 [cP ] and a specific density of 868 [kg/m3].
The analysis of the experimental data obtained was developed using the MATLAB software. The artificial neural network was structured with back-propagation to obtain an accurate holdup predictive model, using the differential pressure as inputs of the neural network, and the superficial velocities of each of the fluids controlled and gradually modified by the LabView™ software. The sigmoid tangent function was used as the activation function.
The selection of predictive model was done by comparing the results obtained by making variations in the number of neurons that make up the two hidden layers of the neural network. The adequate number of neurons was obtained such that, when interrelated with the other structure, generate the least error in the calculation of the holdup of fluids.
3 Design of the Artificial Neural Network
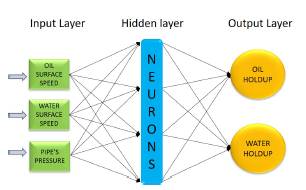
The application of artificial intelligence techniques is particularized in this study to the structuring of a multilayer perceptron artificial neural network based on machine learning. This approach is particularly interesting due to the flexibility it presents in the adaptation and modification of inputs, outputs, and hidden layers, together with its respective synaptic weights and biases, with the application of the sigmoid tangent activation function. The general structure of the artificial neural network is presented in Figure 2.
The net input of the implemented artificial neural network has an internal mathematical design obtained using (1), as shown in [21].
where w ij are the weights that represent the degree of relationship or connection between the nodes i and j, x i are the inputs to the node j, i is the number of nodes and b j is the bias related to each node j, and the hidden layer node is represented by j.
To obtain an accurate model, the sigmoid tangent activation function is implemented for the treatment of input data [22]. Equation (2) shows the mathematical definition of the TanSig activation function.
The input element to the nodes of the next layer is represented by f (S j ), likewise represents the output of the node j. Two important factors in the structuring of the ANN are the synaptic weights and the biases that are directly involved with each input value, representing the level of influence of each variable in the output process, which are generated and adjusted during neural network training.
The design of the artificial neural network was developed using the MATLAB 2019a software, given its applicability and optimal fit in this study.
3.1 Error Evaluation of the Predictive Model
The number of neurons that make up the hidden layers of the neural network increases the complexity of the study, due to the interactions generated by integrating three variables as inputs to the ANN, such as the pressure differential in the pipeline and the superficial velocities of water and oil. Therefore, the mean square error is established as the initial parameter for the selection of an accurate predictive model, which is mathematically represented by (3).
Y Expm is the experimental value of the output, YPred is the output value of the prediction, and n is the total number of input data to the artificial neural network. Additionally, the study of the results includes the absolute average percentage error (AAPE), expressed mathematically in (4), and the coefficient of determination R 2 defined in (5). With these comparison parameters we have enough information to make the proper selection of the predictive model.
4 Results
Table 1 shows the results obtained in the training of the ANN and its validation when applying the TanSig activation function. The table compares the results for MSE, R2, and AAPE for different number of neurons that make up the hidden layers of the network.
Table 1 Results of MSE, R2, and AAPE for different number of neurons in the two hidden layers of the artificial neural network.
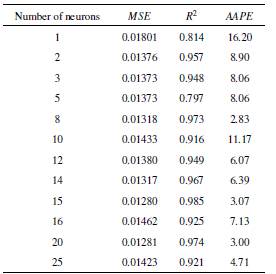
Analyzing this information for the multilayer artificial neural network composed of two hidden layers, three inputs and two outputs, it was possible to determine the ANN that integrates the minimum values of the established parameters. Including in the two hidden layers a number of 15 neurons, we have a MSE of 0.01280 %, a coefficient of determination R2 of 0.985, and a AAPE of 3.07%.
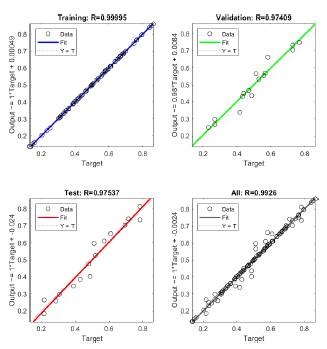
Figure 3 shows the linear behavior of the training, validation, and testing phases, focused on the structuring of the artificial neural network model, for which the final model yields a correlation coefficient R of 0.9926.
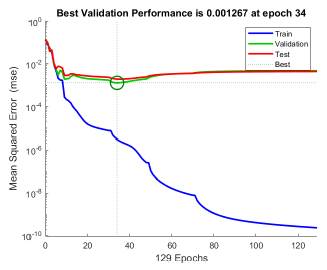
Figure 4 shows the behavior of the MSE as the model development phases progress. The lowest value reached by the MSE in the validation phase was 0.001267 after having advanced 34 epochs out of the 129 used.
5 Conclusions
We presented an efficient predictive model based on machine learning structured in a multilayer perceptron neural network for the calculation of the holdup of biphasic flows. The model considers water and oil fluids that flow through a horizontal circular pipe, and uses experimental data obtained for the surface speed of the fluids and the differential pressure in the pipe.
The predictive model presents minimum values for the MSE = 0.01280 % and AAPE = 3.07% parameters, and a high R2 = 0.985 when 15 neurons are included in the two hidden layers.