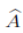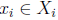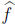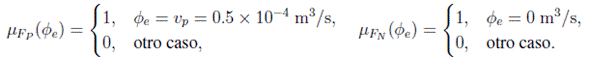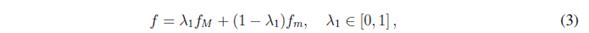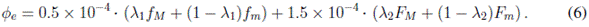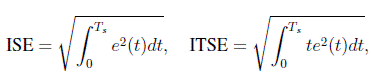1. Introducción1
Los automatismos basados en lógica booleana (también llamada clásica ó bivalente) han sido ampliamente utilizados para controlar distintos fenómenos, por ejemplo, temperatura, nivel, caudal y otros [2]. Estos cuentan con principios básicos de diseñó (como tablas de verdad), y técnicas de simplificación (mapas de Karnaug por ejemplo) que ayudan a su rápido planteamiento, fácil aplicación y bajo costo computacional. Sin embargo, presentan serios inconvenientes a causa de la naturaleza discontinua de la acción de control sobre los fenómenos sobre los que operan.
Buscando mejorar este comportamiento Soriano et. al. [3] propusieron el reemplazo de la lógica booleana por la lógica difusa en el diseñó de automatismos. Esto derivó en un nuevo esquema de inferencia difusa con claras diferencias sobre el esquema clásico propuesto por Mamdani y Assilian [4]. Desde ese entonces han aparecido varias aplicaciones: control de temperatura, control de nivel, control en procesos químicos, control de velocidad de un motor, control de actitud de un satélite, control en conversores DC-DC, identificación de sistemas no lineales, identificación de series de tiempo, identificación de personas, mapas cognitivos difusos, y además estudios teóricos con el fin de consolidar las bases de este sistema de inferencia difusa. Entre estas contribuciones se destaca la realizada por Salazar et. al. [5], que presenta un método para extender funciones booleanas (o de lógica clásica) a funciones regulares2 kleeneanas (o de lógica trivalente de Kleene). Tema con ciertas consecuencias teóricas que son precisamente el punto de partida de este trabajo.
Una de las ventajas de trabajar con funciones kleeneanas para el diseño de controladores difusos está en el hecho de que esta metodología permite proponer bases de reglas en forma de tablas de verdad finitas de tres elementos, que pueden ser representadas mediante fórmulas lógicas fáciles de computar, similar a como se hace en el diseño de automatismos booleanos. La metodología para el diseño y optimización de sistemas de control difuso basados en relaciones booleanas y kleeneanas (FIS-BKR) fue presentada en [7]. Dicha metodología hace amplió uso de la extensión de funciones booleanas a kleeneanas regulares. Sin embargó, la forma de extender una función booleana a una kleeneana regular no es única. Esto en ocasiones convierte el proceso de diseño en un retó debido a que la cantidad de extensiones puede ser enorme e inmanejable. La elección de una extensión regular adecuada para una aplicación particular requiere ciertos criterios de ingeniería.
La propuesta sobre la que se basa este artículo fue introducida en [1]. Se usa la estructura reticular de las funciones kleeneanas que son extensiones regulares de una función booleana dada y la combinación convexa difusa introducida por Zadeh [8]. Esta metodología de diseño cambia el panorama de la optimización de un problema discreto sobre un conjunto finito a uno continuo en un conjunto infinito.
En este artículo se presenta una aplicación al control de nivel de un sistema hidráulico compuesto por un tanque cilíndrico horizontal. Problema que fue trabajado en [9] [12]. Los índices de desempeño que se trabajaron son el ISE (Integral Squared Error) e ITSE (Integral Time-weighted Squared Error) los cuales fueron minimizados en cierto espacio de parámetros relacionados con los coeficientes de la combinación convexa difusa. El control con dicha técnica implicó una mejora en la respuesta del sistema controlado de hasta el 1.427% para el ISE y de hasta 21.99% para el ITSE con respecto al desempeño de las extensiones extremas. Se evidenció la aparición de nuevos puntos de operación que ayudaran al diseñador, y creemos presentan importantes propiedades para futuras aplicaciones.
Consideramos que esta metodología, aparte de simplificar el proceso de diseño, capta la naturaleza de los sistemas de inferencia basados en relaciones algebraicas. Sin embargo, tareas relacionadas con la optimización de parámetros quedan abiertas, y serán clave a la hora de buscar un modelo más completo de este tipo de controladores.
Este documento está divido en tres grandes partes. En la primera se presentan algunos preliminares sobre funciones lógicas así como de controladores FIS-BKR y su metodología de diseño. En la segunda se presenta la propuesta sobre el controlador FIS-BKR con combinador convexo. En la tercera parte se exhibe una aplicación de control de nivel en un tanque cilíndrico, donde se realiza un proceso de sintonización y se presentan los resultados. El documento concluye con una sección de conclusiones.
2. Preliminares
Definición 1 (Lógica trivalente de Kleene). Se denotara por K el álgebra de valores de verdad (K = {0,1/2,1} ; V, Λ,', 0,1), con el orden usual para sus elementos (0 < 1/2 < 1), donde las operaciones disyunción (V) y conjunción (Λ) entre a, b є K están dadas por a V b = max {a, b} y a b = min {a, b}. El complemento (') de a є K es a' = 1 - a. También se identificara el elemento 1/2 con la letra u. En la Tabla I(b) se muestran estas operaciones lógicas actuando sobre K.
Definición 2 (Lógica bivalente de Boole). La restricción de K al conjunto B = {0,1} se conoce como lógica bivalente de Boole (lógica clásica o lógica booleana) y se denota con la letra B. En la Tabla I(a) se muestran las operaciones lógicas actuando sobre B.
Tabla I (a) Operaciones lógicas disyunción (V), conjunción (Λ) y complemento (') en lógica bivalente de Boole. (b) Operaciones lógicas disyunción (V), conjunción (Λ) y complemento (') en lógica trivalente de Kleene.
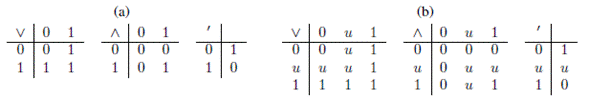
Definición 3 (Lógica difusa estándar). Se denotara por el álgebra de valores de verdad conformada por (I = [0,1]; V, A,', 0,1), con el orden usual para sus elementos, donde las operaciones disyunción (V) y conjunción (Λ) entre a,b є I están dadas por a V b = max {a,b} y a Λ b = min {a, b}. El complemento (') de a є I es a' =1 - a.
el álgebra de valores de verdad conformada por (I = [0,1]; V, A,', 0,1), con el orden usual para sus elementos, donde las operaciones disyunción (V) y conjunción (Λ) entre a,b є I están dadas por a V b = max {a,b} y a Λ b = min {a, b}. El complemento (') de a є I es a' =1 - a.
Observación 1. Aunque K e  no están definidas sobre los mismos conjuntos de valores de verdad, K e
no están definidas sobre los mismos conjuntos de valores de verdad, K e  tienen la misma lógica proposicional [13], es decir, sus proposiciones lógicas son las mismas. Como consecuencia, K permite la elaboración de tablas de verdad y obtención de fórmulas lógicas para
tienen la misma lógica proposicional [13], es decir, sus proposiciones lógicas son las mismas. Como consecuencia, K permite la elaboración de tablas de verdad y obtención de fórmulas lógicas para  , lo cual sería imposible para esta última debido a su carácter infinito.
, lo cual sería imposible para esta última debido a su carácter infinito.
Definición 4 (Funciones de lógica bivalente, trivalente y multivalente). Una función f de n variables se dice función de lógica bivalente (FLB) (o función booleana) si es una aplicación de Bn a B, se dice función de lógica trivalente (FLT) (o función kleeneana) si es una aplicación de Kn a K, y se dice función de lógica multivalente (FLM) si es una aplicación de In a I.
Observación 2. Una caracterización de funciones kleenanas desde un punto de vista más general se encuentra en [14]. Para el propósito de este artículo, una función kleeneana es una aplicación de Kn a K.
Definición 5 (Fórmulas bien formadas). Sea V un conjunto finito de variables. Dadas las constantes 0, u y 1, y los símbolos A, V y ', el conjunto de fórmulas bien formadas F está definido recursivamente como:
Los elementos de F son llamados fórmulas bien formadas, fórmulas lógicas o simplemente fórmulas.
Es conocido que toda FLB es representable a través de una fórmula que no involucra la constante u en ella. Esto es consecuencia del teorema de expansión de Boole. Sin embargo, esto no siempre es cierto para las FLT. Una clase importante de FLT, llamadas regulares, son aquellas que pueden ser representadas por fórmulas.
Definición 6. Se define sobre K el siguiente orden parcial3.  para todo α є K.La relación
para todo α є K.La relación  no compara 0 y 1. Esta relación es extendida a K
n
como sigue: Sean a= (α1,….,α
n
) b = (b1,….b
n
) є K
n
entonces a
no compara 0 y 1. Esta relación es extendida a K
n
como sigue: Sean a= (α1,….,α
n
) b = (b1,….b
n
) є K
n
entonces a  b si, y solo si,
b si, y solo si, para todo i = 1, 2,..., n.
para todo i = 1, 2,..., n.
Definición 7 (Regularidad). Sea ƒ: K
n
→K una FLT. f se dice regular si, y solo si, ƒ (a) є B={0,1} implica ƒ (a) = ƒ (b) para todo .
.
Mukaidono [6] demostró que la regularidad es condición necesaria y suficiente para que una FLT sea representable a través de una fórmula. En esencia, este autor mostró que el conjunto F y el conjunto de las FLT regulares (FLTR) es el mismo. Dado que una FLB (o FLTR) puede tener más de una fórmula, entonces cada FLB (o FLTR) se identificara con su fórmula canónica, también llamada forma normal4.
Ahora, dada una tabla de verdad asociada a una FLB (o FLTR) es de interés conocer su forma normal (conjuntiva y/o disyuntiva). El siguiente procedimiento tomado y adaptado de [13] se usa para este fin. En [13], [15] [17] se probó la existencia y unicidad de las formas normales.
Método 1 (Forma normal disyuntiva [13]).
Para las filas que tienen valor 1 en la columna de ƒ que debe ser puesta en su forma normal disyuntiva: Formar la conjunción de las variables que tienen valor 1 con los complementos de las variables que tienen valor 0 (omitir las variables que tienen valor u).
Para las filas que tienen valor u en la columna de f que debe ser puesta en su forma normal disyuntiva: Formar la conjunción de las variables que tienen valor 1 con los complementos de las variables que tienen valor 0 y la conjunción tanto de la variable como de su complemento para las que tienen valor u.
Formar la disyunción de las conjunciones obtenidas en los dos pasos anteriores. En caso de no existir conjunciones se obtendrá una disyunción vacía que representa la forma normal disyuntiva para 0.
La forma normal disyuntiva kleeneana de ƒ, denotada FNDK(ƒ), se obtiene al descartar conjunciones que tienen los mismos (o posiblemente mas) literales que otras conjunciones.
Observación 3. La forma normal disyuntiva booleana de ƒ, denotada FNDB(ƒ), se obtiene siguiendo los pasos 1 y 3 del Método 1, teniendo en cuenta el valor de f solo en la filas de la tabla de verdad donde aparecen unos y ceros exclusivamente.
Observación 4. Las correspondientes formas normales conjuntivas (kleeneana y booleana), denotadas FNCK(ƒ) y FNCB(ƒ) respectivamente, se obtienen del Método 1 intercambiando las palabras conjunción por disyunción, disyunción por conjunción, ceros por unos, y unos por ceros.
Una forma de obtener fórmulas en  es por medio de K (debido a la igualdad de sus lógicas proposicionales [13]). Dado que B es una restricción de K, una manera de lograr lo anterior es partir de una FLB ƒ, luego extender ƒ a una FLTR g, y posteriormente encontrar una fórmula para g. La fórmula encontrada para g en K es la misma que en
es por medio de K (debido a la igualdad de sus lógicas proposicionales [13]). Dado que B es una restricción de K, una manera de lograr lo anterior es partir de una FLB ƒ, luego extender ƒ a una FLTR g, y posteriormente encontrar una fórmula para g. La fórmula encontrada para g en K es la misma que en  , sin embargo, esta fórmula en
, sin embargo, esta fórmula en  es una FLM. En [5] se propuso el Método 2 para extender una FLB a una (o más) FLTR. De acuerdo a [5], Teorema 3.1, dada ƒ una FLB el Método 2 garantiza que siempre es posible encontrar a lo menos una FLTR g que es extensión de ƒ, pero no necesariamente única.
es una FLM. En [5] se propuso el Método 2 para extender una FLB a una (o más) FLTR. De acuerdo a [5], Teorema 3.1, dada ƒ una FLB el Método 2 garantiza que siempre es posible encontrar a lo menos una FLTR g que es extensión de ƒ, pero no necesariamente única.
Definición 8. Sea ß: Kn→N: a→ ß (a) donde N = {0,1, 2,... ,n}, definida5 como el número total de u en a є Kn.
Método 2 (Extensión [5]).
1. Dada una FLB ƒ: Bn → B de n variables
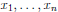 construir una tabla de verdad de 2n filas y n+1 columnas (n columnas para
construir una tabla de verdad de 2n filas y n+1 columnas (n columnas para  y 1 columna para ƒ). Estas filas tendrán las 2
n
combinaciones de valores para
y 1 columna para ƒ). Estas filas tendrán las 2
n
combinaciones de valores para  y los correspondientes valores para ƒ (los cuales son representados como
y los correspondientes valores para ƒ (los cuales son representados como  como se muestra en la Tabla II(a)
como se muestra en la Tabla II(a)
Tabla II (a) FLB inicial ƒ: Bn → B dada como una tabla de verdad. (b) FsLTR g: Kn → K (extensiones de ƒ) dadas como tabla de verdad.

A la tabla elaborada en el numeral 1, agregar 3n - 2n nuevas filas. Primero aquellas
 filas cuya combinación de valores de las variables tienen solamente una u (nivel de ambigüeda d
filas cuya combinación de valores de las variables tienen solamente una u (nivel de ambigüeda d  , enseguida aquellas
, enseguida aquellas 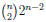 filas cuya combinación de valores de las variables tienen dos u (nivel de ambigüedad
filas cuya combinación de valores de las variables tienen dos u (nivel de ambigüedad , y así sucesivamente. Al final, la tabla finaliza con aquella
, y así sucesivamente. Al final, la tabla finaliza con aquella  1 fila que tiene n valores u en la combinación de valores de sus variables (nivel de ambigüedad
1 fila que tiene n valores u en la combinación de valores de sus variables (nivel de ambigüedad ), como se muestra en Tabla II(b). Cada grupo de filas agregado previamente es separado por una línea horizontal que representa la separación entre diferentes niveles de ambigüedad ß. El nivel de ambigüedad es creciente.
), como se muestra en Tabla II(b). Cada grupo de filas agregado previamente es separado por una línea horizontal que representa la separación entre diferentes niveles de ambigüedad ß. El nivel de ambigüedad es creciente.Hacer gi = ƒi para i = 0,1, 2,..., 2n - 1.
Para cada grupo con nivel de ambigüedad ß = 1.2….,n hacer lo siguiente:
Para la j-ésima fila considerada dentro del grupo con nivel de ambigüedad

 , encontrar aquellas
, encontrar aquellas 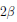 filas en el grupo inmediatamente previo con nivel de ambigüedad
filas en el grupo inmediatamente previo con nivel de ambigüedad  cambiando uno por uno cada u por 0 y 1 sobre la j-ésima fila. Estas 2ß filas son inmediatamente menos o igual de ambiguas que la j-ésima fila de acuerdo a la relación
cambiando uno por uno cada u por 0 y 1 sobre la j-ésima fila. Estas 2ß filas son inmediatamente menos o igual de ambiguas que la j-ésima fila de acuerdo a la relación  definida sobre K y extendida sobre K
n
(Definición 6).
definida sobre K y extendida sobre K
n
(Definición 6).Para cada una de las
 filas encontradas en el numeral 4a, encontrar el conjunto de valores más o igual de ambiguos al respectivo valor g de esa fila. Escribir este conjunto en una columna separada.
filas encontradas en el numeral 4a, encontrar el conjunto de valores más o igual de ambiguos al respectivo valor g de esa fila. Escribir este conjunto en una columna separada.El conjunto de valores que g puede tomar sobre la j-ésima fila considerada es la inter- sección de aquellos conjuntos encontrados en el numeral 4b. Si g puede tomar más de un valor, crear tantas nuevas columnas para nuevas funciones g como sea posible. Para cada g creada, repetir el numeral 4.
Como se mencionó anteriormente, la forma de extender una FLB a una FLTR no es única. Si ƒ es una FLB y 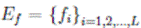 es el conjunto de todas las FLTR que son extensión de ƒ, entonces Eƒ ordenado en el sentido de la Definición 9 forma una estructura de retículo [1] con mínimo y máximo. El conjunto Eƒ es finito dado que L≤ 33", donde n es el número de variables de ƒ.
es el conjunto de todas las FLTR que son extensión de ƒ, entonces Eƒ ordenado en el sentido de la Definición 9 forma una estructura de retículo [1] con mínimo y máximo. El conjunto Eƒ es finito dado que L≤ 33", donde n es el número de variables de ƒ.
Definición 9. Sea ƒ una FLB y sean g y h dos FLTR que son extensión de ƒ. Se dirá que g es menor o igual que h, denotado  , si y solo si,
, si y solo si,  para todo x en el dominio de g y h.
para todo x en el dominio de g y h.
Definición 10 (Funciones extremas). Sean ƒ una FLB y  el conjunto de todas las FLTR que son extensiones de ƒ. Se denotara por ƒ
M
a la extensión máxima en E
ƒ
tal que
el conjunto de todas las FLTR que son extensiones de ƒ. Se denotara por ƒ
M
a la extensión máxima en E
ƒ
tal que  para toda i = 1, 2,... ,L y similarmente por ƒm a la extensión mínima en Eƒ tal que
para toda i = 1, 2,... ,L y similarmente por ƒm a la extensión mínima en Eƒ tal que  para i = 1, 2,..., L.
para i = 1, 2,..., L.
Por definición 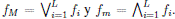 . Si L es grande (y también desconocido a priori) las anteriores expresiones pueden ser poco útiles para su cálculo. La siguiente proposición, demostrada en [1], da expresiones simples para ƒM y ƒ m que no requieren del conocimiento previo de la totalidad de extensiones.
. Si L es grande (y también desconocido a priori) las anteriores expresiones pueden ser poco útiles para su cálculo. La siguiente proposición, demostrada en [1], da expresiones simples para ƒM y ƒ m que no requieren del conocimiento previo de la totalidad de extensiones.
Proposición 1. [1] Sea ƒ una FLB. La forma normal conjuntiva booleana de f es igual a fM y la forma normal disyuntiva booleana de f es igual a ƒm.
Las formulas correspondientes para ƒM y ƒm sobre lógica difusa son FLM. Estas dos FLM pueden ser operadas a través de combinación convexa (Definición 11) para obtener otras FLM, en particular, todas las extensiones en Eƒ vía la Proposición 2. La siguiente es una definición general dada por Zadeh [8].
Definición 11 (Combinación convexa). [8] Sean  funciones definidas sobre un conjunto X no vacío. La combinación convexa de ƒ y g con coeficiente λ, denotada por
funciones definidas sobre un conjunto X no vacío. La combinación convexa de ƒ y g con coeficiente λ, denotada por , es una función
, es una función : X → I dada por
: X → I dada por
Proposición 2. [18], [19] Sean 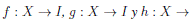 I funciones definidas sobre X. Entonces
I funciones definidas sobre X. Entonces  si, y solo si, existe
si, y solo si, existe  I tal que
I tal que 
La Proposición 2 aplicada a ƒM y ƒm, las extensiones máxima y mínima del conjunto Eƒ = , tomando
, tomando  si, y solo si, existe
si, y solo si, existe  I tal que
I tal que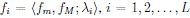 . Entonces todas las extensiones regulares de una FLB pueden ser obtenidas vía combinación convexa. Además, con otras elecciones de
. Entonces todas las extensiones regulares de una FLB pueden ser obtenidas vía combinación convexa. Además, con otras elecciones de  también se pueden obtener otras FLM entre ƒm y ƒM que no están en Eƒ.
también se pueden obtener otras FLM entre ƒm y ƒM que no están en Eƒ.
3. Sistema de inferencia difusa basado en relaciones booleanas y kleeneanas (FIS-BKR)
El sistema de inferencia difusa basado en relaciones 6 booleanas y kleeneanas (Fuzzy Inference System based on Boolean and Kleenean Relations (FIS-BKR)) fue propuesto por primera vez en el año 2001 por Soriano et. al. [3]. La propuesta original ha sido ampliada considerablemente tras casi 16 años de investigación continua y varios nombres han aparecido con el tiempo. La Figura 1 muestra el diagrama de bloques actual. A continuación se presenta el método de diseño propuesto en [7].

Figura 1 Sistema de inferencia difusa basado en relaciones booleanas y kleeneanas (FIS-BKR). Tomado de [7]
Fusificador El fusificador usado es unitario (o singleton en inglés). Para un x* dado, el conjunto difuso unitario A (singleton) a la salida del fusificador está definido por la función de pertenencia:
donde x = (x1,..., xn) є X es el vector de variables de entrada  es un valor particular tomado en la entrada del fusificador y
es un valor particular tomado en la entrada del fusificador y  es el universo de entrada.
es el universo de entrada.
Base de reglas Para la j-ésima salida yj-(j = 1,2,... ,m) del vector de salidas y є Y, donde
 una regla típica de la base de reglas luce
una regla típica de la base de reglas luce
como:
Si  (no) es A
n
entonces y
j
(no) es B,
(no) es A
n
entonces y
j
(no) es B,
donde A i (i = 1,2,..., n) es uno de los posibles conjuntos difusos formulados sobre el i-ésimo universo de entrada X i y B es uno de los posibles conjuntos difusos formulados sobre el j-ésimo universo de salida Yj.
Las operaciones lógicas “y”, “o” y “no” son las dadas por la lógica difusa estándar 7 y/o lógica booleana. La formulación de los conjuntos difusos sobre cada universo de entrada y salida puede seguir algún criterio Figura 2(a) y Figura 2(b)), por ejemplo, puede obedecer a la definición de partición difusa
[17], def. 7.4.1. Además, cada conjunto difuso B formulado sobre el j-ésimo universo de salida  debe tener un único valor característico
debe tener un único valor característico  llamado actuador virtual.
llamado actuador virtual.

Figura 2 (a) Ejemplo de formulación de conjuntos difusos en el j-ésimo universo de entrada X
i
(i =1, 2,..., n). Se muestra la función de pertenencia de uno de los conjuntos difusos A. (b) Ejemplo de formulación de conjuntos difusos en el j-ésimo universo de salida Y
j
(j = 1,2,..., m). Se muestra la función de pertenencia de uno de los conjuntos difusos B con su valor característico  llamado actuador virtual.
llamado actuador virtual.
Motor de inferencia El diseño del motor de inferencia se realiza en dos etapas:
En la primera se hace una aproximación a través de lógica booleana,
y en la segunda se hace una extensión a la lógica difusa estándar a través de lógica trivalente.
A continuación se explican los pasos a seguir en cada etapa.
Etapa 1: Aproximación a través de lógica booleana
Aproximación de conjuntos difusos mediante conjuntos bivalentes Todos los conjuntos de los antecedentes de las reglas son aproximados mediante conjuntos bivalentes, esto es, si A es uno de los posibles conjuntos difusos formulados sobre el i-ésimo universo de entrada
 , entonces este conjunto es aproximado mediante un conjunto bivalente
, entonces este conjunto es aproximado mediante un conjunto bivalente  con función de pertenencia bivalente (es decir,
con función de pertenencia bivalente (es decir, 
Codificación bivalente de las regiones aproximadas de operación Cada conjunto bivalente
 formulado en el paso anterior realiza una partición del universo de entrada
formulado en el paso anterior realiza una partición del universo de entrada  en la siguiente forma:
en la siguiente forma:
En este paso es posible realizar una codificación bivalente de todas las posibles regiones aproximadas de operación 8 mediante una tabla de verdad de lógica bivalente (ceros y unos), basados en la partición descrita anteriormente. Cada codificación corresponderá a una fila de la tabla. Si después de codificar todas las posibles regiones aproximadas de operación aún existen códigos por asignar, estos códigos son tratados como condiciones no importa.
Asignación de las acciones del sistema en las regiones aproximadas de operación
Sobre la tabla de verdad del paso anterior, crear una función booleana
 por cada actuador virtual
por cada actuador virtual  perteneciente a cada conjunto difuso B formulado sobre el j-ésimo universo de salida
perteneciente a cada conjunto difuso B formulado sobre el j-ésimo universo de salida . El valor de
. El valor de  en la respectiva codificación (fila de la tabla) dependerá de la acción que tomara el sistema en la respectiva región aproximada de operación. Cada función
en la respectiva codificación (fila de la tabla) dependerá de la acción que tomara el sistema en la respectiva región aproximada de operación. Cada función  es llamada salida de activación (del respectivo actuador virtual v) y corresponderá con una columna de la tabla. Sobre las filas de la tabla consideradas como condiciones no importa el valor de
es llamada salida de activación (del respectivo actuador virtual v) y corresponderá con una columna de la tabla. Sobre las filas de la tabla consideradas como condiciones no importa el valor de  es arbitrario y puede ser elegido con algún criterio dado por el diseñador.
es arbitrario y puede ser elegido con algún criterio dado por el diseñador.Obtención de fórmulas Para cada función booleana
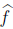 creada en el paso anterior obtener su forma normal (disyuntiva o conjuntiva) booleana, donde las variables de dicha fórmula son las funciones de pertenencia de cada conjunto bivalente.
creada en el paso anterior obtener su forma normal (disyuntiva o conjuntiva) booleana, donde las variables de dicha fórmula son las funciones de pertenencia de cada conjunto bivalente.Simplificación (optimización) de fórmulas Para cada formula obtenida en el paso anterior aplicar la versión de lógica booleana del método de simplificación 9 (optimización) de fórmulas propuesto en [20].
Etapa 2: Extensión a la lógica difusa mediante lógica trivalente de Kleene
En este paso es posible realizar una codificación trivalente de todas las posibles regiones de operación mediante una tabla de verdad de lógica trivalente (0, u y 1), basados en la partición descrita anteriormente. Cada codificación corresponderá con una fila de la tabla. Esta codificación trivalente debe preservar en su totalidad la codificación bivalente obtenida en la primera etapa. De esta forma la tabla de verdad de lógica trivalente es una extensión de la correspondiente de lógica bivalente
Obtención de fórmulas lógicas difusas Para cada función kleeneana regular ƒ seleccionada en el paso anterior obtener su forma normal (disyuntiva o conjuntiva) kleeneana.
6. Simplificación (optimización) de fórmulas lógicas difusas Para cada formula obtenida en el paso anterior aplicar la versión de lógica trivalente de Kleene del método de simplificación (optimización) de fórmulas propuesto en [20]
Defusificador El vector de salidas y є Y, donde 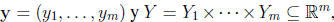 se calcula por medio de un defusificador basado en formulas lógicas (booleanas y/o kleeneanas). Estas fórmulas ponderan el valor del respectivo actuador.
se calcula por medio de un defusificador basado en formulas lógicas (booleanas y/o kleeneanas). Estas fórmulas ponderan el valor del respectivo actuador.
La j-ésima salida y
j
(j = 1, 2,..., m), correspondiente al j-ésimo universo de salida Yj donde se tienen k actuadores virtuales que están siendo ponderados por k formulas lógicas
que están siendo ponderados por k formulas lógicas  dadas por el motor de inferencia, está dada por (Figura 3):
dadas por el motor de inferencia, está dada por (Figura 3):

Figura 3 Diagrama de bloques del Defusificador para la j-ésima salida yj (j = 1, 2,…,m), basado en las formulas lógicas (booleanas y/o kleeneanas)  y actuadores virtuales v
ij
y actuadores virtuales v
ij
De acuerdo a Espitia y Soriano [9], [21], v ij es llamado actuador virtual, f ij es llamada salida de activación y el producto f ij v ij es llamado salida virtual. Estos nombres corresponden al hecho que en lógica booleana fij є {0,1} y en logica difusa f ij є [0,1], por lo tanto fij (al ser adimensional y construido usando la respectiva logica) actúa como un activador/desactivador del actuador vij. Además, vij al ser un elemento del respectivo universo de salida Y i tiene las mismas dimensiones de este último, por lo que funciona como un actuador. El termino virtual corresponde al hecho que vij (dependiendo de la aplicación) podría (o no) tener alguna correspondencia con latín elemento físico real donde el sistema difuso está actuando.
Concresor Históricamente se ha denominado Concresor a la unión entre el Motor de Inferencia y el Defusificador (Figura 1). El Concresor es aquel bloque que realiza la concrecion 11 de la información difusa.11
4. FIS-BKR con combinador convexo
En algunas aplicaciones la selección de las extensiones regulares en el paso 4 de la segunda etapa del diseño del motor de inferencia puede ser una tarea difícil, principalmente por su gran número. La propuesta dada en [1] está en la adición de un bloque llamado Combinador Convexo12 justo antes del Defusificador y después del motor de inferencia. Esto permite integrar todas las extensiones regulares kleeneanas. En la Figura 4 se muestra el diagrama de bloques del combinador convexo.

Figura 4 Diagrama de bloques del combinador convexo con coeficiente λij (x) є [0,1] para la i-ésima función booleana  formulada sobre el j-ésimo universo de salida (j= 1,2,..., m). FNCB
formulada sobre el j-ésimo universo de salida (j= 1,2,..., m). FNCB  y FNDB
y FNDB corresponden a la forma normal conjuntiva y disyuntiva booleanas de
corresponden a la forma normal conjuntiva y disyuntiva booleanas de  , respectivamente.
, respectivamente.
El proceso de diseño del FIS-BKR con combinador convexo es el mismo al presentado en la Sección 3 con las siguientes modificaciones en el diseño del motor de inferencia:
Etapa 1: Aproximación a través de lógica booleana
Aproximación de conjuntos difusos mediante conjuntos bivalentes. Igual al paso 1, etapa 1, Sección 3.
Codificación bivalente de las regiones aproximadas de operación Igual al paso 2, etapa 1, Sección 3.
Asignación de las acciones del sistema en las regiones aproximadas de operación Igual al paso 3, etapa 1, Sección 3.
Obtención de fórmulas Para cada función booleana
 creada en el paso anterior obtener su forma normal disyuntiva y conjuntiva booleana, donde las variables de dicha fórmula son las funciones de pertenencia de cada conjunto bivalente. La forma normal disyuntiva booleana de
creada en el paso anterior obtener su forma normal disyuntiva y conjuntiva booleana, donde las variables de dicha fórmula son las funciones de pertenencia de cada conjunto bivalente. La forma normal disyuntiva booleana de  corresponde a
corresponde a  (extensión regular mínima) y la forma normal conjuntiva booleana de
(extensión regular mínima) y la forma normal conjuntiva booleana de  corresponde a
corresponde a  (extensión regular máxima).
(extensión regular máxima).Simplificación (optimización) de fórmulas Este paso no se realiza.
Etapa 2: Extensión a la lógica difusa mediante lógica trivalente de Kleene
Retrosustitucion de conjuntos difusos Igual al paso 1, etapa 2, Sección 3.
Codificación trivalente de las regiones de operación Este paso no se realiza.
Extensión a la lógica difusa (por medio de la lógica trivalente de Kleene) Este paso no se realiza.
Selección de las extensiones regulares adecuadas Este paso no se realiza.
Obtención de fórmulas lógicas difusas Este paso no se realiza.
Simplificación (optimización) de fórmulas lógicas difusas Este paso no se realiza.
Obtención de combinaciones convexas Para cada extensión mínima
 y máxima
y máxima  encontrada en la etapa 1 obtener su combinación convexa difusa con coeficiente λ definido por el diseñador. El coeficiente λ puede ser seleccionado con algún criterio dependiendo de la aplicación.
encontrada en la etapa 1 obtener su combinación convexa difusa con coeficiente λ definido por el diseñador. El coeficiente λ puede ser seleccionado con algún criterio dependiendo de la aplicación.
5. Aplicación
La siguiente aplicación muestra el uso del método de diseño de controladores FIS-BKR con combinador convexo difuso. Esta aplicación fue presentada por Espitia [9] y Salazar [20], y previamente por Lara [12], Hernández [11] y Tunyasrirut [10] donde se propusieron otras soluciones de control empleando lógica difusa.
5.1. Modelo dinámico
Se desea mantener el nivel h(t), siendo t la variable tiempo, de cierta cantidad de líquido en un tanque cilíndrico en posición horizontal donde el flujo de salida  varía a través de la válvula VS. Existen dos válvulas de flujo de entrada. La primera (VG) deja entrar un flujo grande
varía a través de la válvula VS. Existen dos válvulas de flujo de entrada. La primera (VG) deja entrar un flujo grande  de líquido mientras que la segunda (V
P
) deja entrar un flujo pequeño
de líquido mientras que la segunda (V
P
) deja entrar un flujo pequeño  El flujo total de entrada está dado por
El flujo total de entrada está dado por  como se muestra en la Figura 5(a). Las variables y constantes del sistema con sus unidades se muestran en la Tabla III.
como se muestra en la Figura 5(a). Las variables y constantes del sistema con sus unidades se muestran en la Tabla III.
Tabla III Variables y constantes del sistema de llenado de un tanque cilíndrico en posición horizontal


Figura 5 (a) Sistema de llenado de un tanque cilíndrico en posición horizontal. (b) Geometría del tanque cilíndrico en posición horizontal
La Figura 5(b) muestra la geometría del tanque donde (r/2)2 + (R - h)2 = R2, por lo tanto al despejar r se tiene  . El diferencial de volumen del líquido en el tanque está dado por
. El diferencial de volumen del líquido en el tanque está dado por , siendo H = 2R. Para esta aplicación se supone que la densidad del líquido del tanque
, siendo H = 2R. Para esta aplicación se supone que la densidad del líquido del tanque 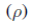 es constante y la misma que la del líquido entrante y saliente. La ecuación de conservación de la masa para este sistema es:
es constante y la misma que la del líquido entrante y saliente. La ecuación de conservación de la masa para este sistema es:  donde m es la masa de líquido del tanque, me es la masa entrante y ms la masa saliente. Esta ecuación se puede simplificar a
donde m es la masa de líquido del tanque, me es la masa entrante y ms la masa saliente. Esta ecuación se puede simplificar a  son los flujos de entrada y salida, ve y vs son los volúmenes de líquido entrante y saliente, y usando las ecuaciones
son los flujos de entrada y salida, ve y vs son los volúmenes de líquido entrante y saliente, y usando las ecuaciones  . Sustituyendo el diferencial de volumen dv encontrado antes y despejando para dh/dt se obtiene:
. Sustituyendo el diferencial de volumen dv encontrado antes y despejando para dh/dt se obtiene:  . Dado que la válvula de salida se encuentra en la parte inferior del tanque y actúa por acción de la gravedad, el flujo de salida está dado por
. Dado que la válvula de salida se encuentra en la parte inferior del tanque y actúa por acción de la gravedad, el flujo de salida está dado por 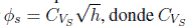 es la constante de la valvula VS. Se obtiene entonces la siguiente ecuación que modela el sistema:
es la constante de la valvula VS. Se obtiene entonces la siguiente ecuación que modela el sistema:
La Figura 6(a) presenta un diagrama de bloques de la anterior ecuación diferencial.
5.2. Diseño de un controlador FIS-BKR con combinador convexo
La Figura 6(b) muestra el diagrama de bloques de la estrategia de control elegida. Esta consiste en un esquema de retroalimentación de la variable nivel h, comparada contra una altura de referencia Href, para obtener el error e = Href - h, que junto a su derivada, serán las entradas del controlador FIS-BKR con combinador convexo tipo proporcional-derivativo (PD). La salida del controlador es el flujo de entrada al tanque  .
.

Figura 6 (a) Diagrama de bloques del sistema de llenado del tanque cilíndrico en posición horizontal. (b) Control usando FIS-BKR con combinador convexo.
Aproximación a través de lógica booleana Para el error de nivel e se definen dos conceptos: error positivo (EP) y error negativo (EN) con las siguientes funciones de pertenencia (Figura 7):

Figura 7 (a) Conjuntos asociados al error positivo y negativo. (b) Conjunto asociado a la derivada del error positiva
Para la variable de/dt se define un solo concepto: derivada positiva (DP) con la siguiente función de pertenencia:
Para la variable de flujo de entrada  se definen cuatro conceptos: flujo grande (F
G
), flujo mediano (F
M
), flujo pequeño (F
P
) y flujo nulo (F
N
) con las siguientes punciones de pertenencia:
se definen cuatro conceptos: flujo grande (F
G
), flujo mediano (F
M
), flujo pequeño (F
P
) y flujo nulo (F
N
) con las siguientes punciones de pertenencia:
La Tabla IV muestra las acciones de control, similares a las presentadas en [9], con funciones de activación  para las válvulas V
G
y V
P
para así obtener los valores de flujo grande, mediano, pequeño y nulo con la activación y desactivación de V
G
y V
P
.
para las válvulas V
G
y V
P
para así obtener los valores de flujo grande, mediano, pequeño y nulo con la activación y desactivación de V
G
y V
P
.
Extensión a la lógica difusa estándar y uso del combinador convexo El primer paso consiste en suavizar los conceptos booleanos cambiándolos por difusos. Los conjuntos difusos para los respectivos conceptos del antecedente son los siguientes:
Las funciones de pertenencia para los conjuntos difusos del consecuente son los mismos que para el caso booleano. Figura 8.

Figura 8 (a) Conjuntos difusos asociados al error positivo y negativo. (b) Conjunto difuso asociado a la derivada del error positiva
Las formas normales (disyuntiva y conjuntiva) booleanas para las funciones de activación  de la Tabla IV llevan a las extensiones kleeneanas extremas asociadas a
de la Tabla IV llevan a las extensiones kleeneanas extremas asociadas a  , las cuales son:
, las cuales son:
Estas fórmulas en lógica trivalente de Kleene pueden ser entendidas como formulas en lógica difusa estándar basados en la teoría expuesta en [13], [15]-[17].
Los coeficientes de la combinación convexa fueron tomados como conjuntos difusos con pertenencia constante. Esto significa que  para todo x, con i = 1, 2. Las expresiones para las funciones de activación f y F están dadas por:
para todo x, con i = 1, 2. Las expresiones para las funciones de activación f y F están dadas por:
Para obtener la acción de control (flujo de entrada)  se ponderan (3) y (4) con actuadores virtuales
se ponderan (3) y (4) con actuadores virtuales  como sigue:
como sigue:
Notar que las unidades de  son las mismas que las unidades de los actuadores virtuales v
p
y v
g
dado que las funciones de activación f y F son adimensionales. La Figura 9 muestra las superficies de control extremas para el flujo de entrada.
son las mismas que las unidades de los actuadores virtuales v
p
y v
g
dado que las funciones de activación f y F son adimensionales. La Figura 9 muestra las superficies de control extremas para el flujo de entrada.
Cabe anotar que si las expresiones (3) y (4) son evaluadas para los conceptos de lógica booleana (1) y (2), las extensiones máximas y mínimas coinciden. Esto implica que f = fM = fm y F = Fm = Fm, es decir, no hay sensibilidad a los parámetros de la combinación λ. En la Figura 10 se muestra el diagrama de bloques del controlador FIS-BKR diseñado.
5.3. Resultados
La implementación del sistema de control se realizó mediante la simulación del sistema dinámico en el entorno de programación visual Simulink de MATLAB13. Se usó un tiempo de simulación Ts = 5000 s y pasos de tiempo de  . Teniendo como flujo de entrada al tanque:
. Teniendo como flujo de entrada al tanque:
Al variar los parámetros λ1 y λ2, el sistema controlado presenta distintas repuestas temporales. En la Figura 11 se presenta la respuesta del controlador booleano (sin suavización de los conceptos), al tiempo que se exhiben respuestas para algunos parámetros de combinación convexa. Se observa que los controladores presentan error en estado estacionario y diferentes tiempos de establecimiento. Llama la atención la respuesta del sistema para los parámetros 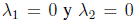 puesto que no hay establecimiento alguno del nivel. La razón de este comportamiento está asociada a la magnitud del flujo de entrada que en este caso es la acción de control mínima posible ( ecuación (6)). Este comportamiento muestra clara evidencia de un hecho importante: no todo controlador FIS-BKR diseñado a partir de un controlador booleano que aproxima la referencia controla el sistema.
puesto que no hay establecimiento alguno del nivel. La razón de este comportamiento está asociada a la magnitud del flujo de entrada que en este caso es la acción de control mínima posible ( ecuación (6)). Este comportamiento muestra clara evidencia de un hecho importante: no todo controlador FIS-BKR diseñado a partir de un controlador booleano que aproxima la referencia controla el sistema.
En la Figura 11 se observa que el control booleano presenta cierta variabilidad consecuencia de la discontinuidad de los conceptos, situación que no ocurre cuando estos son suavizados, como se propone en la metodología de diseño de controladores FIS-BKR.
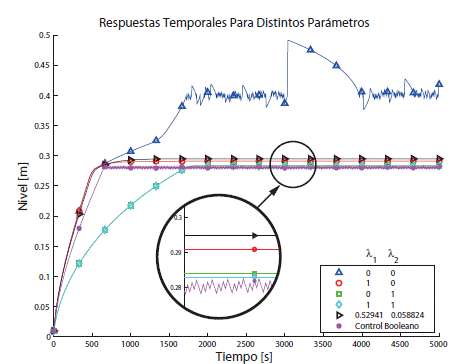
Figura 11 Respuesta temporal de la variable nivel para el sistema controlado para diferentes coeficientes de combinación convexa.
Evaluación de índices de desempeño Es de nuestro interés evaluar para el sistema controlado los índices de desempeño ITSE e ISE. Para este caso se usó la definición discreta de tales índices donde se remplaza la integral por una sumatoria y los valores de error son muestreados. Estos índices están definidos por:
donde e(t) = Href - h(t) es el error de nivel y Ts es el tiempo de simulación. Estos criterios de un solo número dan cuenta del cuadrado del error en el tiempo. El primero favorece sistemas con respuestas que se acercan a una referencia dada, mientras que el segundo, por tener en cuenta el tiempo usado para alcanzarla, es menor para sistemas que lo hacen rápidamente. La Figura 12 muestra cómo cambian los anteriores índices de desempeño con la variación de los parámetros λ1y λ2.

Figura 12 (a) Valores del índice ISE para diferentes valores de λ1 y λ2. (b) Valores del índice ITSE para diferentes valores de λ1 y λ2.
El proceso de optimización de los índices ISE e ITSE se realizó mediante la evaluación de una rejilla de 16 x 16 puntos en el dominio [0,1] x [0,1], el cual tomo un tiempo de 35 minutos y 30 segundos14. Se obtuvieron los parámetros óptimos  para ambos índices. La Tabla V resume los valores que optimizan los índices de estudio, además de presentar el desempeño del sistema de control booleano.
para ambos índices. La Tabla V resume los valores que optimizan los índices de estudio, además de presentar el desempeño del sistema de control booleano.
Tabla V índices ISE e ITSE para las extensiones extremas fm, fM, Fm, FM y valores de los coeficientes A1 y A2 que minimizan ambos índices (negrilla).

En este caso el proceso de optimización llevo a una mejora de hasta el 1.427% para ISE y de hasta 21.99% para el ITSE con respecto al desempeño de las extensiones extremas. Sin embargo, cabe notar que no se puede concluir que este controlador óptimo sea mejor que cualquier extensión algebraica ya que esta aplicación se limitó exclusivamente a coeficientes con pertenencia constante. Por otro lado, la simple validación de si lo es o no resulta una tarea extensa como se verá a continuación.
Conteo de extensiones Por último, con el fin de mostrar al lector lo complejo que puede ser buscar la mejor extensión algebraica dado un índice de desempeño por el método tradicional (Sección 3), en la Tabla VI se muestran las extensiones posibles de la función  de la Tabla IV obtenidas al aplicar el Método 2.
de la Tabla IV obtenidas al aplicar el Método 2.
Donde “-” representa una condición de no importa y pueden valer 0, 1 o u, teniendo en cuenta las condiciones de regularidad. Para conocer la cantidad de extensiones es necesario realizar el producto de las posibilidades de cada fila, lo cual, sin tener en cuenta las condiciones de no importa, es de a lo menos 26 = 64. Esta sería la cantidad de funciones kleeneanas regulares que se tendrían
operativo: Windows 10 de 64 bit, Version MATLAB: 7.12.0 (R2011a).
que evaluar como mínimo para elegir la mejor, no sin antes encontrar sus fórmulas lógicas lo cual de por sí es una tarea ardua.
6. Conclusiones y comentarios finales
Este artículo presento nueva evidencia de las características favorables de controladores FIS-BKR con combinador convexo difuso cuando se evaluaron los índices de desempeño ISE e ITSE. Basados en hechos teóricos se puede asegurar que la estrategia de control FIS-BKR con combinador convexo difuso y su metodología de diseño generalizan el FIS-BKR actual, permitiendo así trabajar con un modelo más completo, como lo demuestra una mejora en el desempeño de 1.427% para el ISE y 21.99% en el caso del ITSE, comparados con las alternativas extremas del FIS-BKR y un controlador basado en logica booleana.
Por el carácter global que tienen las funciones extremas, se puede decir que la información obtenida de la etapa de diseño con lógica booleana está siendo incorporada sin sesgo alguno y sin mayor complejidad; ya que se obtiene a partir de las alternativas extremas, sin necesidad de pasar por métodos computacionalmente costosos de deducción de fórmulas que requieren otras extensiones, solucionando en cierto modo algunas de las desventajas mencionadas por Salazar en [7].
Tanto el estudio de la simplificación de fórmulas representadas mediante formas normales, como la caracterización de las familias de coeficientes-parámetro para el proceso de sintonización serían importantes aportes en la fundamentación del uso del combinador convexo, que por su novedad, ha sido poco estudiada. Así mismo, consideramos que el estudio de otras técnicas de optimización en dominios compactos para el proceso de sintonización, diferentes al de “fuerza bruta” que fue utilizada, es indispensable cuando la cantidad de parámetros sea considerablemente grande, ya que hacerlo con una técnica poco sofisticada podría resultar inviable.