REVISIÓN DE LITERATURA

Modelos de evaluación genética multirracial caso peso al destete en bovinos

Models for multibreed genetic evaluation weaning weight in cattle

Oscar Vergara G,^{1, 2}* Ph.D, Mario Cerón M,² Ph.D, Mauricio Elzo A, ³ Ph.D.

¹Universidad de Córdoba, Facultad de Medicina Veterinaria y Zootecnia, Departamento de Ciencias Pecuarias, Montería, Colombia.
²Universidad de Antioquia, Facultad de Ciencias Agrarias, Grupo de Genética y Mejoramiento Animal, Medellín, Colombia.
³University of Florida, Department of Animal Sciences, Gainesville.

*Correspondencia: overgara@sinu.unicordoba.edu.co

Recibido: Febrero 15 de 2009; Aceptado: Agosto 20 de 2009.

RESUMEN

Los modelos de evaluación genética multirracial permiten la obtención de los valores genéticos de animales perteneciente a una población de diferente composición racial. La estructura de este tipo de modelo va a depender de la característica a evaluar y de la población multirracial a ser analizada, obteniendose al final de la evaluación valores genéticos aditivos y no aditivos, los cuales permiten tomar decisiones y direccionar los apareamientos de una forma más acertada.

Palabras clave: Bovinos, multirracial, peso al deteste.

ABSTRACT

Multibreed genetic evaluation models allow the prediction of animal breeding values in a population of animals of various breed compositions. The structure of this type of model depends on the traits to be evaluated and the multibreed population to be analyzed, and they eventually yield additive and nonadditive animal genetic values, which allow more precise selection decisions and mating plans.

Key words: Bovines, multibreed, weaning weight.

INTRODUCCIÓN

Todos los modelos animales se caracterizan por la evaluación de los valores de cría, merito genético total o la predicción de los registros futuros de todos los individuos en la población de interés (1). Dependiendo de las características consideradas en la evaluación y de la estructura de los datos, diferentes modelos pueden ser utilizados para la predicción de los valores genéticos de los individuos, por lo que se han desarrollado modelos específicos para la aplicación a determinadas características y estructura de datos (2).

Importación de semen, embriones, y de animales vivos ha contribuido a que la mayoría de los sistemas de producción de carne y leche utilicen animales de diversa composición racial. Colombia en particular tiene una gran diversidad de animales Criollos, que sumados a la disponibilidad de animales de razas extranjeras, ha permitido la creación de una tremenda diversidad genética bovina. Esto indica la necesidad de desarrollar sistemas de evaluación genética que sean capaces de evaluar a todos los animales en poblaciones compuestas de animales puros y cruzados en Colombia.

En este trabajo se discutirá al rededor de evaluaciones multirraciales con énfasis en factores que se deben considerar para su implementación, se describirán varios modelos multirraciales y se explicarán los tipos de evaluaciones genéticas producidos por evaluaciones multirraciales y su posterior uso para seleccionar animales por valores genéticos aditivos, no-aditivos y totales.

MODELO ANIMAL PARA POBLACIONES MULTIRRACIALES

Poblaciones multirraciales. Las poblaciones multirraciales se definen como aquellas compuestas por la reproducción cruzada de animales de razas puras y sus cruzamientos. En las poblaciones multirraciales, padres y madres pueden ser de cualquier composición racial (3,4). Según el esquema de apareamientos, las poblaciones multirraciales pueden ser clasificadas como completas o incompletas. Las poblaciones multirraciales completas presentan un esquema total de apareamiento dialélico, esto es, los grupos de padres y madres son los mismos y los padres son apareados con madres de cualquier grupo racial (3,4). En poblaciones multirraciales incompletas los toros y/o las vacas no están representados en algunos de los grupos raciales, y los toros pueden no ser apareados con vacas de todos los grupos raciales. Además, gran parte de las poblaciones multirraciales experimentales y comerciales en todo el mundo encajan en la definición de multirraciales incompletas (4).

Modelo multirracial. Los modelos de evaluación genética multirracial son simplemente extensiones de los modelos genéticos intra-raciales que tienen en cuenta los efectos genéticos aditivos y no aditivos dentro y entre razas. En éstos modelos, los efectos genéticos aditivos son el resultado de la combinación de los efectos genéticos aditivos dentro y entre razas (4). Haciendo referencia a lo anterior, en una población multirracial se definen tres tipos de efectos genéticos: multirraciales aditivos, que se deben a los efectos acumulados de todos los genes que afectan un carácter y se predicen como desvío del valor de cada animal relativo al de la base genética multirracial aditiva; multirraciales no aditivos, que se refieren a las interacciones entre genes de una o más razas que resultan de la interacción de los alelos de un toro y de los alelos de todas las vacas apareadas con este toro y se predicen como desvíos del valor de las interacciones interraciales de un animal relativo al de la base no aditiva genética interracial; y multirraciales totales, que hacen referencia a la suma de los valores genéticos aditivos más las interacciones genéticas interraciales y se predicen como la suma de los correspondientes valores genéticos predichos aditivos y no aditivos (5-8).

En poblaciones multirraciales los animales cruzados sirven como unión entre las poblaciones parentales de razas puras, generando así mismo, una población multirracial simple compuesta de animales puros y cruzados, por lo que los datos de estas poblaciones deben ser analizados usando procedimientos multirraciales, que tengan en cuenta los efectos genéticos aditivos y no aditivos, como también la heterogeneidad de varianzas y covarianzas dentro de grupos de razas puras y cruzadas. Mientras que, si son usados procedimientos intra-raciales para analizar datos multirraciales, estos no explican los efectos genéticos no aditivos, asumiendo que todas las características presentan las mismas varianzas y covarianzas en todos los grupos raciales (razas puras y cruzadas) (4). Las estrategias computacionales necesarias para construir las ecuaciones del modelo mixto multirracial son más complejas que aquellas para los modelos intra-raciales. La diferencia principal es la heterogeneidad de varianzas y covarianzas genéticas y ambientales de los modelos multirraciales (9,10).

La forma que pueden tomar los modelos de evaluación genética multirracial depende de la población multirracial a ser analizada, es así como Elzo (11) y Elzo y Famula (12) y posteriormente Arnold et al (13), propusieron el modelo animal para poblaciones multirraciales como una necesidad de desarrollar procedimientos que incluyan animales de diversa composición genética. Elzo y Famula (12), advierten que para bases de datos de programas de cruzamiento abierto pueden existir problemas de confusión en los efectos fijos genéticos, debido a subclases vacías, lo cual es confirmado por Rodríguez-Almeida et al (2), al afirmar que el desarrollo de este modelo está limitado a la estructura de la base de datos, donde el número de razas o cruces pueden ser una limitante. La heterogeneidad de varianzas genética aditiva, genética no aditiva y ambiental será fácil de estimar en poblaciones multirraciales balanceadas, pero probablemente será imposible estimarla en poblaciones multirraciales altamente no balanceadas, en donde los toros están pobremente representados mediante grupos raciales de vacas. La aplicación de modelos de evaluación genética multirracial a bases de datos comerciales precisa tener en cuenta los siguientes aspectos (4):

1) Conexión entre grupos contemporáneos multirraciales: similar a las evaluaciones unirraciales, en las multirraciales, los grupos contemporáneos deben estar conectados a través del uso de padres en común. Estos padres pueden ser de razas puras o cruzados. Lo ideal sería realizar estas conexiones con padres de todos los grupos raciales representados en cada grupo contemporáneo para evitar problemas de interacciones entre grupos raciales de padres y grupos contemporáneos multirraciales (13,14). Los procedimientos de evaluación genética multirracial requieren que los descendientes de varios grupos raciales combinados sean conservados sobre las mismas condiciones ambientales. La definición de grupos contemporáneos para procedimientos de evaluación genética multirracial, es similar a los procedimientos intrarraciales (15).

2) Estimación de varianzas y covarianzas multirraciales: la estimación de los componentes de varianza y covarianza, dependen en gran medida del buen balanceamiento de la población multirracial, del nivel de conexión (grupos raciales y animales) y de la cantidad de información disponible por animal (4). Algo que en la práctica es muy difícil, ya que por lo general se encuentran variedad de grupos raciales y pocos individuos por grupo racial.

3) Elección de una base genética multirracial: se bebe escoger una base genética multirracial para facilitar las comparaciones de los animales de razas puras y cruzados por medio de grupos raciales y tipos de apareamiento. Una base que tenga dos componentes: uno genético aditivo, similar a las bases genéticas dentro de razas, y uno genético no aditivo, para comparar combinaciones de apareamientos (4).

4) Decisión sobre cuales desvíos esperados de predicción multirracial (DEPM) específicos predecir: la decisión de obtener predicciones de DEPNM (desvíos esperados de predicción multirracial no aditivo) e DEPTM (desvíos esperados de predicción multirracial total) regularmente dependerá en gran medida de las frecuencias esperadas de apareamientos de toros y vacas de composiciones raciales particulares (4).

5) Desarrollo de medios apropiados para divulgar las DEPM: una publicación de resúmenes de toros impresos para las DEPAM podría, sobre ciertas circunstancias, ser una alternativa apropiada y económicamente viable. No obstante, una publicación impresa de las DEPNM y DEPTM sería probablemente limitada a un pequeño número de toros ampliamente usados (ej.: toros usados para conectar rebaños multirraciales). Una publicación electrónica de sumarios de toros completos para DEPAM parece ser una alternativa económicamente más viable (4).

6) Explicación de las diferencias entre predicciones genéticas aditivas, no aditivas y totales y su uso para la selección y las decisiones de direccionamiento genético. Para que las DEPAM, DEPNM y DEPTM sean efectivamente usadas, deben ser interpretadas correctamente. Es responsabilidad de las entidades que efectúan las evaluaciones multirraciales explicar claramente su uso adecuado para propósitos comerciales y de selección. Las DEPAM deben ser usadas de la misma forma como se usan las DEP dentro de raza (para seleccionar animales para efectos genéticos aditivos). La principal diferencia entre ambas es que las DEPAM son predichas con relación a una base genética más amplia, o sea, ellas pueden ser usadas para comparar animales de todas las posibles proporciones de las razas base dentro de la población multirracial. No obstante, las DEPAM de animales de diferentes poblaciones multirraciales con por lo menos una raza base diferente no pueden ser comparadas (4).

Arnold et al (13) propusieron el modelo animal para la evaluación simultánea de animales de diferente composición genética, el cual permite el análisis simultáneo de datos de múltiples poblaciones de razas puras, como también de la progenie resultante del cruzamiento. Además, afirmaron que los datos fenotípicos son típicamente representados en el modelo animal simple como una combinación de efectos fijos de grupos contemporáneos, efectos genéticos aditivos y efecto aleatorio del error, en el modelo animal multirracial, este es expandido para incluir efectos genéticos no aditivos, quedando el modelo de la forma:

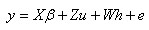, donde:

y = es el vector de observaciones;
X = es la matriz de incidencia que relaciona las observaciones a los efectos fijos de (b)
Z = es la matriz de incidencia que relaciona las observaciones al vector de efectos genéticos aditivos totales (u);
W = es la matriz de incidencia que relaciona las observaciones al vector de efectos genéticos no aditivos totales (h); y
e = es el vector de efectos aleatorios residuales.

Una modificación inicial a la expresión anterior, precisamente en la partición de u en componentes fijo y aleatorio. El vector de los efectos genéticos aditivos totales (u), pueden ser expresados como (16,17):

donde;

Q = es la matriz que relaciona animales en el vector u a grupos raciales puros en el vector φ, a través de las fracciones de razas puras presentes en cada animal;
φ = es el vector de efectos fijos aditivos de los grupos raciales puros;
a = es el vector de los efectos aleatorios genéticos aditivos.

Similarmente, el vector de efectos genéticos no aditivos totales (h) relacionado a la heterosis, puede ser particionado en componentes fijo y aleatorio, quedando de la forma:

donde;

S = es la matriz de incidencia conocida que relaciona el vector de efectos genéticos no aditivos totales (h) al vector de efectos fijos de heterosis (γ);
T = es la matriz de incidencia que relaciona el vector de efectos genéticos no aditivos totales (h) al vector de efectos aleatorios de heterosis (d).

La magnitud de los valores diferentes a cero en S y T está determinada por la heterocigosis de las progenies, la cual depende de la composición racial de los padres. El efecto fijo de heterosis representa el promedio de las habilidades combinatorias de todos los animales apareados en una población. El efecto aleatorio de heterosis (d) reconoce que existe variabilidad en la habilidad combinatoria de padres y madres. Se considera que en el mejor de los casos la posibilidad de predicción individual de valores aleatorios de heterosis es problemática, y puede ser impracticable en poblaciones reales. En ciertas poblaciones se tendría que suponer que el componente fijo de heterosis es suficiente (13). Sustituyendo a u y h en la ecuación inicialmente planteada se tiene:

donde:

y = es el vector de observaciones;
X = es la matriz de incidencia que relaciona observaciones a efectos fijos (β);
ZQ = son matrices de incidencia que relacionan observaciones al vector de efectos fijos aditivos de grupos raciales puros (φ);
Z = es la matriz de incidencia que relaciona observaciones al vector de efectos aleatorios genéticos aditivos (a);
WS = son matrices de incidencia que relacionan observaciones al vector de efectos fijos de heterosis (γ);
WT = son matrices de incidencia que relacionan observaciones al vector de efectos aleatorios de heterosis (d); y
e = es el vector de efectos aleatorios residuales.

Para el modelo, el primer y segundo momento están dados por:

y

Al especificar una estructura apropiada para las diferentes matrices y vectores involucrados se tiene:

Donde el modelo mixto de ecuaciones estará dado por:

En este modelo mixto de ecuaciones, los elementos de las matrices y vectores se representan de la forma M_ij, donde i = (1, 2, x), corresponde a los animales de las razas 1, 2 o cruzados, respectivamente, y j = (p,n), es la porción de la matriz o vector correspondiente a los registros de padres y no padres, respectivamente.

Las matrices de incidencia X y Z tienen básicamente la misma estructura que las usadas comúnmente en el análisis de intrarracial. La matriz Q relaciona animales puros y cruzados en el vector u a grupos raciales puros. Para animales puros, cada fila de la submatriz Q_ij tiene un solo 1, el cual relaciona al individuo con el elemento adecuado del vector de grupos raciales puros (φ). Para animales cruzados, cada fila tiene coeficientes diferentes a cero, correspondientes a la composición fraccional de la raza del animal. Si todos los animales tienen registros, Z es una matriz identidad. Si los padres no poseen registros son representados en Z por una columna de ceros.

La matriz incidencia para S y T puede ser representada simbólicamente como:

Las matrices S y T relacionan el efecto fijo y aleatorio del efecto de heterosis contenidos en los registros fenotípicos de los animales cruzados. Datos de individuos puros podrían ser representados en S y T por filas de ceros y padres sin progenies cruzadas podrían tener una columna nula en T.

La organización de los vectores φ, γ, d y e, sería de la forma:

Donde el vector a_ij, i = {1, 2, x} representa la desviación genética aditiva dentro de φ para individuos de las razas 1, 2 o cruzadas, respectivamente. El vector γ_ij, (i, j={1, 2} i no= j) es el vector de efectos fijos de la interacción (heterosis). Para características que no tienen influencia materna, se puede hacer la asunción que γ₁₂ = γ₂₁.

El vector de efectos aleatorios no aditivos d_ip,12, i = {1,2,x} representa la desviación aleatoria dentro del efecto fijo de heterosis representado por γ₁₂. En un análisis de más de dos razas, el efecto fijo de heterosis puede ser modelado por cada combinación de razas. En general, d_ip,jk, contendría elementos que representan una desviación de los padres dentro de d_jk, donde jk sería un tipo particular de apareamiento (13).

La estructura de la matriz de la varianza residual para un modelo multirracial es la siguiente:

Donde la inversa (R^-1) es el reciproco de cada uno de los elementos de la diagonal.

El modelo planteado por Arnold et al (13) es la base para el planteamiento de otros modelos que puedan incluir efectos genéticos directos y maternos o cualquier otro efecto que pueda ser considerado para estimados confiables de las evaluaciones genéticas.

Rodríguez-Almeida et al (2), al realizar un estudio sobre el efecto directo y materno para el peso al nacer y a los 200 días en tres poblaciones multirraciales hizo una simplificación del modelo presentado por Arnold et al (13), quedando éste representado de la siguiente manera:

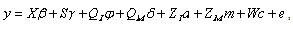donde:

y = vector de observaciones;
β = vector de efecto fijo del grupo contemporáneo;
γ = vector de efectos de heterosis directa y materna;
φ y δ = vectores de efectos fijos directo y materno de la raza, respectivamente;
a = vector aleatorio de efecto genéticos aditivo directo;
m y c = vectores de efectos aleatorios genético aditivo y ambiental permanente materno;
e = vector de residuales;
X = matriz incidencia con ceros y unos que relaciona observaciones a grupos contemporáneos;
Q_I y Q_M = matrices incidencia que relacionan observaciones a efectos directos y maternos de la raza a través de las fracciones raciales de animales (f_il) y de madres (f_jl), respectivamente; y
Z_I, Z_M y W = matrices incidencia con ceros y unos que relacionan las observaciones a efectos genéticos aditivos directos, aditivos maternos y de ambiente permanente, respectivamente. Z_I y Z_M serán aumentadas con 0 en las columnas para animales sin registros que fueron incluidos en la matriz de relación aditiva.

En un trabajo sobre predicción de efectos genéticos aditivos y no aditivos para el peso al destete en un rebaño multirracial Angus x Brahmán, se encontraron exactitudes muy bajas, debido al pequeño componente de varianza utilizado en dicho estudio y al escaso número de progenies por grupo racial de las vacas que cada toro tuvo en la población (18).

En un estudio sobre características de crecimiento predestete se estimaron los componentes de varianza y las diferencias esperadas de progenies de efectos genéticos directos y maternos aditivas y no aditivos en una población multirracial Angus X Brahman, en el cual se utilizó el siguiente modelo mixto (19):

Donde:

y : vector of observaciones para peso al nacer y al destete;
b: vector de efectos de grupo contemporáneo (b_cg) y edad de la madre dentro del sexo de la cría (b_adx);
g_a: vector de efectos genéticos aditivos directo dentro de la raza A (g_Aad), materno dentro de la raza A (g_Aam) , directo interracial AB (g_ABad) , y materno interracial AB (g_ABam);
g_n: vector de efectos del grupo genético interracial A/B no aditivo directo (g_A/Bnd) y materno (g_A/Bnm);
g_mgd: vector de efectos del grupo genético de abuela materna;
s_a: vector de efectos genéticos aditivos directos del padre (s_ad) y materno (s_am).
s_n: vector de efectos genéticos no aditivos directo (s_nd) y materno (s_nm);
v: vector de residuales;
X: matriz que relaciona los registros de las crías con 1) los elementos de b_cg (de unos y ceros) y 2) los elementos de b_adx a través de la edad de la madre y la fracción esperada de alelos A en la madre de la cría;
Z_ga: matriz que relaciona los registros de las crías con 1) elementos de g_Aad a través de la fracción esperada de alelos de A en el padre y abuelo materno de la cría (p_As + .5p_Am), 2) elementos de g_Aam a través de la fracción esperada de alelos A en el abuelo materno de la cría (p_Am), 3) elementos de g_ABad a través de la probabilidad de alelos A y B en los padres del padre y el abuelo materno de la cría [(pAss pBss + pAds pBds) + 0.5(pAsd pBsd + pAdd pBdd)], 4) elementos de gABam a través de la probabilidad de alelos A y B en los padres del abuelo materno de la cría (p_Asd p_Bsd + p_Add p_Bdd), donde p = probabilidad y A = Angus, B = Brahman, s = padre, m = abuelo materno, ss = padre del padre, ds = madre del padre, sd = padre de la madre (abuelo materno), dd = madre de la madre;

Z_gn: matriz que relaciona los registros de la cría con 1) elementos de gnd a través de la probabilidad de alelos intralocus A y B en la cría (p_As p_Bd + p_Bs p_Ad), 2) elementos de gnm a través de la probabilidad de alelos intralocus A y B en la madre de la cría (p_Asd p_Bdd + p_Bsd pA_dd);

Z_a: matriz que relaciona los registros de la cría con 1) elementos de s_ad a través del padre (1) y el abuelo materno (0.5), 2) elementos de s_am a través de abuelo materno (1);

Z_n: matriz que relaciona los registros de la cría con 1) elementos de s_nd a través de la probabilidad de alelos intralocus en la cría (p_As p_Bd + p_Bs p_Ad), 2) elementos de s_nm a través de la probabilidad de alelos intralocus A y B en la madre de la cría (p_Asd p_Bdd + p_Bsd p_Add); y

Z_mgd: matriz que relaciona los registros de la cría con los elementos de gmgd a través de la fracción esperada de alelos A en la abuela materna.

El modelo mixto de ecuaciones utilizado fue el siguiente:

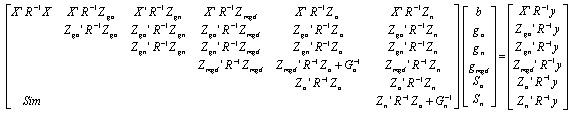
En este trabajo para estimar las diferencias esperadas de progenie multirracial aditiva se utilizó la siguiente expresión:

Donde:

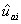: es la diferencia esperada en progenie multirracial directa o materna para el padre i;
: es la fracción esperada de la raza X (X=A, B) en el grupo racial del animal k, k=i, s (padre del padre i), d (madre del padre i);

: es el mejor predictor lineal insesgado de .

Las diferencias esperadas de progenie multirraciales no aditivas se calcularon a través de la formula:

: es la diferencia esperada en progenie multirracial no aditiva directa o materna para el padre i;

: es la fracción esperada de la raza X (X=A, B) en el padre i;

: es la fracción esperada de la raza X (X=A, B) en la madre del grupo racial d apareada con el padre i;

: es el estimado por mínimos cuadrados generalizados de

: es el mejor predictor lineal insesgado de. S_ni

Y las diferencias esperas de progenies multirraciales totales a través de la ecuación:

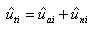
En esta investigación se encontraron estimados de covarianza genética intrarracial e interracial aditivo e interracial no aditivo, como se muestra en la Tabla 1 (19). Se puede notar que los valores estimados de covarianza genética aditivo interracial fueron muy diferentes de las covarianza intrarracial, esto debido al efecto de la heterocigosis en los animales cruzados. Además, se observa covarianza negativas entre el efecto directo y materno intrarracial y en el interracial AB, causada posiblemente por el tamaño de la población utilizada.

Elzo y Wakeman (19), estimaron además las heredabilidades y las correlación genética para el peso al destete, donde en términos generales todos los parámetros fueron de valores medio a bajo (Tabla 2). Las heredabilidades estimadas con relación al efecto directo y al materno para los diferentes tipos de apareamiento fueron un poco diferentes, por lo tanto, el efecto materno debe ser considerado dentro del modelo al hacer la evaluación del peso al destete. Además, se ven valores negativos de la correlación genética entre el efecto aditivo directo y el materno.

Debido a la complejidad que presentan los modelos de evaluación genética multirracial y a la estructura de las bases de datos, se han realizados algunos trabajos que no incluyen los efectos aleatorios genéticos no aditivos (Tabla 3), incluyendo solo efectos fijos (grupos contemporáneos y efecto de raza), efectos aleatorios genéticos aditivos y efectos fijos no aditivos (heterosis), ya que la mayoría de los programas computacionales de evaluación genética no están diseñados para análisis multirracial completo(20).

Valores Genéticos para poblaciones Multirraciales

El objetivo de una evaluación genética multirracial es el de predecir los efectos genéticos multirraciales aditivos, no aditivos, y totales de los animales utilizando información de animales de todos los grupos raciales. Cada animal va a tener: una predicción aditiva, múltiples predicciones no aditivas, una por cada tipo de cruzamiento (intrarracial e interracial) considerado, y múltiples predicciones totales (aditivas + no aditivas), una por cada tipo de cruzamiento (intrarracial e interracial) considerado. La razón para tener múltiples predicciones no aditivas y totales, es que la probabilidad de tener interacciones interraciales en un locus va a ser diferente dependiendo de la composición racial del grupo con el cual se aparee un individuo (4,5).

Los valores multirraciales de predicción se les denominan desvíos esperados de predicción multirraciales (DEPM). Las siglas para los diferentes efectos genéticos evaluados por animal serían DEPMA para los aditivos, DEPMN para los no aditivos, y DEPMT para los totales. Estos valores predichos aditivos (DEPMA), no aditivos (DEPMN), y totales (DEPMT) se utilizarán para seleccionar los mejores toros, vacas, y terneros de acuerdo a criterios de selección definidos por los productores y(o) genetistas. Si emplean varios caracteres, estos criterios de selección probablemente ponderarán estas predicciones con algún valor económico (5).

Por último, considerando la gran variabilidad genética que existe en Colombia, se considera de gran importancia las evaluaciones genéticas multirraciales en ganado bovino en todas las etapas del crecimiento de los animales y en los diversos ambientes, en busca de direccionar los apareamientos utilizados en los sistemas de producción. Por lo tanto, se debe disponer de base de datos solidas y completa, que permitan estimados de DEP multirraciales lo más confiable posible, para lo cual la colaboración de los productores es de gran importancia. Teniendo en cuenta el modelo animal que considere todas las relaciones genéticas será el mejor método de análisis para datos provenientes de cruzamientos (27)

REFERENCIAS

1. Henderson CR. Theoretical basis and computational methods for a number of different animal models. Proc. Animal model Workshop. J Anim Sci 1988; 71(Supl.2): 1-16.        [ Links ]

2. Rodríguez-Almeida FA, Van Vleck LD, Gregory KE. Estimation of direct and maternal breed effects for prediction of expected progeny differences for birth and weaning weights in three multibreed populations. J Anim Sci 1997; 75: 1203-1212.        [ Links ]

3. Elzo MA. Multibreed evaluation theory and application. Seventh Genetic Prediction Workshop, Kansas City, MI, Dic 3 1999. (accesado diciembre 23 del 2007) Disponible en: http://www.animal.ufl.edu/elzo/Publications/Proceedings/MultEval-TnP-t.htm        [ Links ]

4. Elzo MA, Borjas A. Perspectivas da avaliação genética multirracial em bovinos no Brasil. Ciên Ani Bras 2004; 5:171-185.        [ Links ]

5. Elzo MA, Martinez G, Manrique C. Multibreed genetic evaluation and its application to Criollo cattle breeding programs. Pag. 150-158 in Proc. Census and Characterization of Colombian and Criollo Cattle Production Systems Agricultural Colombian Institute, Bogotá, Colombia. 1999 (accesado 8 de octubre del 2006). Disponible en: http://www.animal.ufl.edu/elzo/Publications/Proceedings/CriolloConf1999-a.htm        [ Links ]

6. Elzo MA. Unconstrained Procedures for the Estimation of Positive Definite Covariance Matrices Using Restricted Maximum Likelihood in multibreed Populations. J Anim Sci 1996; 74:317-328.        [ Links ]

7. Elzo MA. Restricted Maximum Likelihood Procedures for the Estimation of Additive and Nonadditive Genetic Variances and Covariances in Multibreed Populations. J Anim Sci 1994; 72:3055-3065.        [ Links ]

8. Elzo MA. Evaluación genetic multiracial en poblaciones bovinas. Rev Col Cien Pec 2007; 20:504-507.        [ Links ]

9. Elzo MA. Recursive Procedures to compute the inverse of the multiple trait additive genetic covariance matrix in inbred and noninbred multibreed populations. J Anim Sci 1990; 68: 1215-1228.         [ Links ]

10. Elzo MA. Covariances among sire × breed group of dam interaction effects in multibreed sire evaluation procedures. J Anim Sci 1990; 68: 4079-4099.        [ Links ]

11. Elzo MA. Multibreed sire evaluation within and across countries. PhD Dissertation. University of California, Davis, CA, USA. 1983.        [ Links ]

12. Elzo MA, Famula TR. Multibreed sire evaluation procedure within a country. J Anim Sci 1985; 60: 942-952.        [ Links ]

13. Arnold JW, Bertrand JK, Benyshek LL. Animal model for genetic evaluation of multibreed data. J Anim Sci 1992; 70: 3322-3332.        [ Links ]

14. Elzo MA. Genetic evaluation of animals in multibreed cattle populations using linear models. Arch LatinAmer Anim Prod 2006; 14:154-160.        [ Links ]

15. Elzo MA. Considerations for the genetic evaluation of straightbred and crossbred bulls in large multibreed populations. Proc. Symp. WRCC-100, Brainerd, MN. 1995. p. 1-21.         [ Links ]

16. Quaas RL, Pollak EJ. Modified equations for sire models with groups. J Dairy Sci 1981; 64: 1868-1978.        [ Links ]

17. Famula TR, Pollak EJ, Van Vleck LD. Genetic groups in dairy sire evaluation under a selection model. J Dairy Sci 1981; 66:927-934.        [ Links ]

18. Manrique C, Elzo MA, Odenya W, McDowell L, Wakeman D. Predicción de efectos genéticos aditivos y no aditivos del peso al destete mediante un procedimiento de evaluación animal multirracial. Revista Corpoica. 1997; 2(1):17-21        [ Links ]

19. Elzo MA, Wakeman DL. Covariance components and prediction for additive and nonadditive preweaning growth genetic effects in an Angus-Brahman multibreed herd. J Anim Sci 1998; 76: 1290-1302        [ Links ]

20. García-Cortés L, Toro M. Multibreed analysis by splitting the breeding values. Genet Sel Evol 2006; 38: 601-615.        [ Links ]

21. Demeke S, Neser FEC, Schoeman SJ. V ariance components and genetic parameters for early growth traits in a mixed population of purebred Bos indicus and crossbred cattle. Livest Prod Sci 2003; 84: 11-21.        [ Links ]

22. Rosales J, Elzo MA, Montaño M, Vega V, Reyes A. Genetic parameters for birth and weaning weight in Simmental - Brahmán herds under Mexican subtropical conditions. Tec Pecu Mex 2003; 42: 333-346.        [ Links ]

23. De los Reyes A, Elzo MA, Fries LA, Roso VM, Carvalheiro R. Non-genetic, additive and non-additive genetic effects for animal model analyses of weaning weights in a nellore x hereford multibreed population in brazil. 8th World Congress on Genetics Applied to Livestock Production. August 13-18, Belo Horizonte, MG, Brasil 2006 (accesado 14 de abril del 2010). Disponible en: http://www.wcgalp8.org.br/wcgalp8/articles/paper/3_540-1492.pdf.        [ Links ]

24. Bocchi AL, De Oliveira H, Ferraz JB, Eler JP. Avaliação genética multirracial para ganho de peso pré-desmama em bovinos de uma população composta. R Bras Zootec 2008; 37: 1207-1215.        [ Links ]

25. Vergara OD, Cerón-Muñoz MF, Arboleda EM, Orozco Y, Ossa GA. Direct genetic, maternal genetic, and heterozygosity effects on weaning weight in a Colombian multibreed beef cattle population. J Anim Sci 2009.87:516-521.         [ Links ]

26. Brandt H, Müllenhoff A, Lambertz C, Erhardt G, Gauly M. Estimation of genetic and crossbreeding parameters for preweaning traits in German Angus and Simmental beef cattle and the reciprocal crosses. J Anim Sci 2010; 88: 80-86.        [ Links ]

27. Arthur PF, Hearnshaw H, Stephenson PD. Direct and maternal additive and heterosis effects from crossing Bos indicus and Bos taurus cattle: cow and calf performance in two environments. Livest Prod Sci 1999; 57: 231- 241.        [ Links ]